关于一阶线性非齐次微分方程解法的探究

王 满

（四川工商学院计算机学院，四川 眉山 620000）

微分方程章节是微积分课程的重要组成部分，是微积分理论在各领域中的具体应用。微分方程已经在自然科学、工程技术、生物学、物理学、化学等学科中崭露头角。在研究某些现象的变化过程中，往往需要建立待求函数的导数或微分之间的关系式，通过求解关系式去探索待求函数的某些特征。在求解一阶线性非齐次微分方程时，课本［1］和参考书上均使用常数变易法，步骤清晰，层层递推，比较容易求解出通解。但编者在介绍常数变易法时，直接给出待定函数，不仅没有给出常数变易法（也可称为参数变易法或变易常数法）的理论依据，也没有说明待求函数的结构特点以及齐次微分方程的解与非齐次微分方程的解存在何种内在联系，令读者费解。基于课本解法，文章首先介绍微积分理论，解决这些疑问。然后介绍求解一阶线性非齐次微分方程的两种新解法——积分因子法和变量变换法。最后举例并验证这两种方法的正确性和有效性，并与课本方法做比较。

1 一阶线性微分方程

形如

的方程，由于方程中导数的最高阶数是1，y,y2都是一次有理式，故称为一阶线性微分方程。其中，p(x),q(x)均为的连续函数。

鉴于药品行业的特殊性，在政府全面放开药品定价的当下，如何构建完善的药品价格垄断规制框架、在兼顾各方利益的同时保障药品行业平稳有序发展，是当前最需要探索的课题。

当q(x)≡0时，(1)式被称为一阶线性齐次微分方程。

当q(x)不恒等于零时，(1)式被称为一阶线性非齐次微分方程。

根据齐次微分方程和非齐次微分方程解的结构定理［1］知，非齐次微分方程的通解等于相应的齐次微分方程的通解加上非齐次微分方程的一个特解。所以接下来，先讨论一阶线性齐次微分方程通解。

1.1 一阶线性齐次微分方程

形如

的微分方程称为一阶线性齐次微分方程。(2)式本质上是可分离变量的微分方程，求解时需要用到最基本的方法——分离变量法。具体步骤如下:

对照组患者给予多西他赛联合顺铂、氟尿嘧啶静脉治疗，试验组患者给予多西他赛联合顺铂、氟尿嘧啶腹腔灌注，多西他赛注射液（江苏恒瑞医药股份有限公司，国药准字H20020543）第1天和第2天1000 mg/（m2·d）静脉滴注，氟尿嘧啶注射液（上海旭东海普药业有限公司，国药准字H31020593）500 mg/（m2·d）静脉滴注，顺铂注射液（齐鲁制药海南有限公司，国药准字H20073652）75 mg/（m2·d）静脉滴注，腹腔灌注应用热化疗灌注机将顺铂75 mg/（m2·d）和氟尿嘧啶500 mg/（m2·d）分别溶于42～45℃的生理盐水内，3周为1个周期，共计化疗3个周期。

第二步:两边同时积分得通解:

其中，C是任意积分常数。

这种方法简单易懂，步骤简略。使用的理论依据是不定积分，寻找原函数。

解:分离变量得

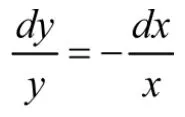
两边同时积分，得到

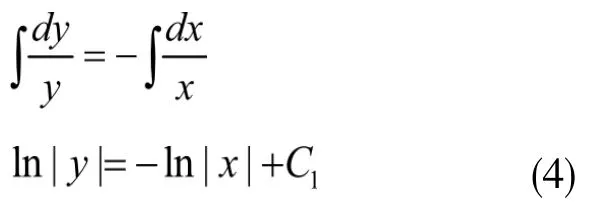
其中，C1为任意常数。

通过调查问卷分析形成各类图书阅读不均的原因，跟读者的自身阅历、喜好、知识积累以及个人需求有关。通过分析宁夏图书馆读者的阅读喜好，有助于确定各类读者的图书采购量和控制副本量，使有限的购书经费得以充分发挥，避免造成不必要的浪费，也有助于平衡各层次读者的阅读需求和对图书馆的满意度。

余额宝社区服务点，其概念来自于美国等西方金融发达国家的“社区银行”，其中的“社区”并不是一个严格界定的地理概念，既可以指一个省、一个市或一个县，也可以指城市或乡村居民的聚居区域。凡是资产规模较小、主要为经营区域内中小企业和居民家庭服务的地方性小型提供购买余额宝购买服务、转出服务以及收益查看服务的服务点都可称为余额宝社区服务点。

LONG Jun-rui, SHAN Chan-juan, YANG Qun-di, LIU Xin-ying, WANG Jiu-sheng, MEI Chang-lin, XIONG Lin-ping

第二步:将y,y′代入原方程，得u′v+u(v′+vcosx)=e-sinx。

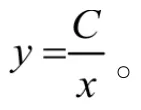
为了方便简化推导过程，以后在微分方程中遇到原函数是对数函数时，直接不用加绝对值符号。即(4)式变为lny=-1nx+lnC，则通解为xy=C。

1.2 一阶线性非齐次微分方程

的通解，其中q(x)不恒等于零。求此方程的通解，课本上使用的方法是——常数变易法。具体步骤如下:

第二步:常数变易，设C=u(x)，求出y,y′。

第三步:将y,y′代入(5)式中，解出

猪水肿病是猪大肠杆菌病肠毒血症引起的一种急性病，以发病突然、头面部水肿和运动失调为主要特点。本病多发于即将断奶或断奶后1～2周龄的仔猪，死亡率高，常为吃食好、生长快、体型大的健壮仔猪发病。

第四步:将u(x)代入第二步中的表达式，得到(5)式的通解

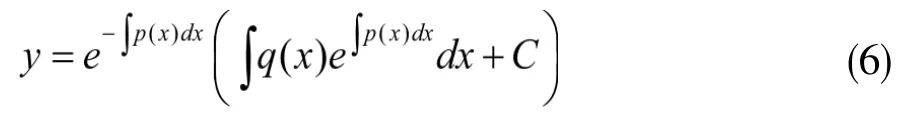
该方法过程简洁明了，层次清晰，使用方便。但书本并未给出方程式(2)和(5)的内在联系，也就是没说明为什么要将C变为u(x)，变了之后的为什么是(5)式的特解。课堂上，如果直接给出这个形式，学生肯定是有疑问的。带着这样的疑问，备课时，我仔细专研教材和微分方程理论，发现了求解(5)式的其他解法，揭示一阶线性齐次微分方程和一阶线性非齐次微分方程的解的内在联系，并找到了常数变易法的根本依据。

为原微分方程的通解，其中C为任意常数。

对于一阶线性非齐次微分方程(5)式，大家都知道这是不可分离变量的微分方程，因此不能使用分离变量法。但由于常数变易法尚未阐述清楚，所以致力于寻找其他解法，很幸运发现了巧妙的诀窍。

所有检测结果均以平均值±标准偏差（±sd，n=3）表示。数据采用Excel和SPSS 20.0对数据进行单因素分析（ANOVA）检验不同样品间的差异显著性，所有差异分析均在p=0.05水平进行。

因此，通解为

先举个例子，一阶线性非齐次微分方程

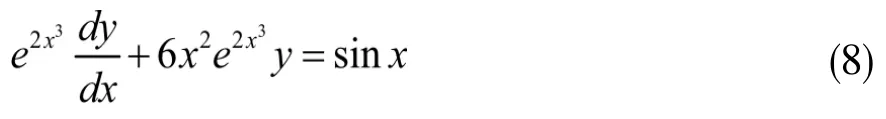
但其实还有更有趣的作用。根据隐函数的求导法则的逆过程得到

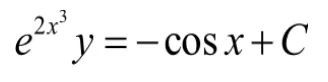
即

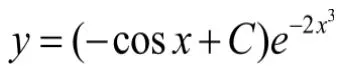
第一种——积分因子法。

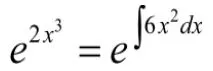
讨论(1)式对应的一阶线性非齐次微分方程

两组患者干预前的FMA评分无明显差异(P>0.05),观察组干预后FMA评分明显较对照组高(P<0.05),见表1。

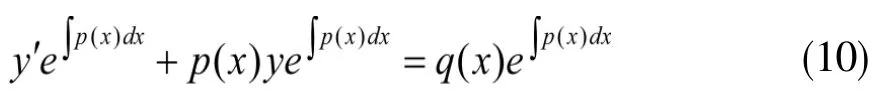
第二步:由隐函数的求导法则的逆运算得:

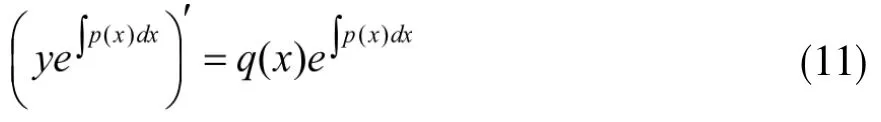
1.对网络课程框架结构进行实用性设计——主要包括知识结构设计和系统功能设计。课程结构设计的重点是对专业知识的学习。由于成人学员存在工学矛盾等客观原因，他们更加重视利用有限的时间，学习实用性较强的专业技能和文化知识，因此，课程框架设计要符合网络课程的开放性、自主性、互动性、共享性等基本特点。

总而言之，实行本科生导师制这一教育改革措施，满足了当前教育发展的需求，也有利于培养国家需要的高素质创新型人才。北京农学院动物医学专业实行本科生导师制尚处于起步阶段，与其他高校相比还存在很大的差距，需要不断探索和研究，不断完善和进步，从而取得更加有效的成果。■

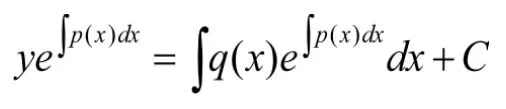
第四步:两边除以积分因子，得通解:

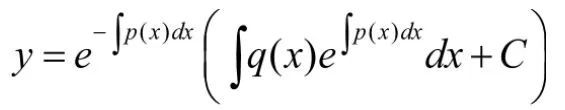
接下来，我们再来讨论第二种——变量变换法。

对于上述例子，一阶线性非齐次微分方程

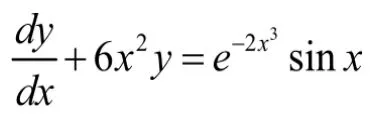
通过观察发现方程右端为函数乘积的形式，猜想解也为函数乘积的形式。于是，先假设该微分方程的一个解为y=uv（u，v为x的函数），利用乘积的求导法则得y′=u′v+uv′。代入原方程得u′v+u(v′+。为了解出u，v函数，先令v′+6x2v=0，解得再根据u′=sinx得u=-cosx。同样得到微分方程的特解为所以通解为。

上述方法是通过分析了微分方程的系数和组成部分，先猜想再验证。这种方法的具体步骤如下:

第一步:设解为y=uv（u，v为x的函数），则y′=u′v+uv′。

第二步:将y,y′代入到(5)式中，得

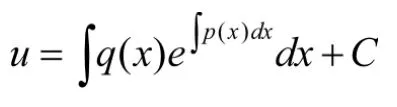
第四步:得出(5)式通解为

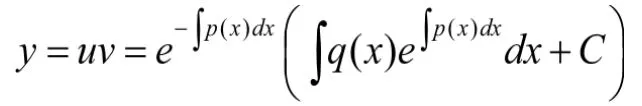
上述阐述了两种新方法，接下来，通过例子说明这两种方法的正确性和有效性，同时对比四种方法的求解步骤和过程。

2 举例验证

该方程为一阶线性非齐次微分方程，分别利用四种解法求解。

解法1——<积分因子法>

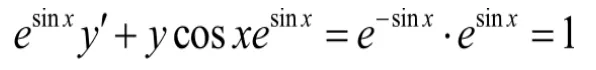
第二步:由隐函数的求导法则的逆运算得:

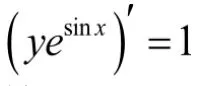
第三步:两边同时积分得:

绍圣四年（1097），山谷《跋自作草后》：“余寓居开元寺之怡偲堂，坐见江山，每于此中作草，似得江山之助。然颠长史、狂僧皆倚酒而通神入妙。余不饮酒忽十五年，虽欲善其事，而器不利，行笔处时时蹇蹶，计遂不得复如醉时书也。”元丰七年（1092）三月，山谷作《发愿文》曰“愿从今日尽未来世，不复饮酒”，至绍圣四年（1097），已十五年。张旭、怀素作草皆以醉酒而忘我迷狂，纵横挥洒，变幻莫测，出神入化。山谷不饮酒，行笔处时时蹇蹶。山谷此时追求“通神入妙”，故而感慨。

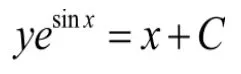
第四步:两边除以积分因子，得通解:

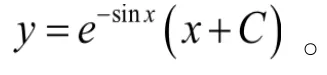
解法2——<变量变换法>

第一步:设特解为y=uv（u，v为x的函数），则y′=u′v+uv′。

xy=C，

第三步:两边同时积分:

第三步:令v′+vcosx=0，则v=e-sinx，代回第二步得u=x。

第四步:将u，v代入第一步得出特解为y=xe-sinx(x+C)，则通解为y=e-sinx(x+C)。

传统Fenton反应速率常数k1为0.0470 min-1，而加入石墨烯的Fenton反应速率常数k2为0.0632 min-1，则k2>k1。由此可知，相比传统Fenton反应，石墨烯的加入提高了Fenton氧化的反应速率，对制浆中段废水的降解效果更显著。

解法3——<常数变易法>

家长助教活动主要是指家长在幼儿园教师的指导下，有效地配合教师开展的协助幼儿学习的活动。在《幼儿园教育指导纲要（试行）》中，针对家长助教提出：教师可以在尊重、平等、自愿的原则上吸引家长主动地参与到幼儿园的教育工作中来，使家长成为幼儿园教师的重要合作伙伴，使幼儿家庭与幼儿园之间更加和谐，使幼儿能够在众多家长的鼓励下获得更多的知识。有了家长的帮助，不但可以活跃教学氛围，还可以把家长自身的教育资源合理地加以发掘和利用，使幼儿通过家长助教学习到更多的知识，获得更好的发展。所以，幼儿园应该在充分重视家长助教工作，针对如何指导家长有效地开展助教进行探索和尝试，使家长助教获得积极发展。

第一步:不难求出该方程对应的齐次微分方程的通解为y=Ce-sinx。

第二步:令常数变易，设y=u(x)e-sinx，则

y′=u′(x)e-sinx-u(x)cosxe-sinx。

第三步:将y,y′代入原方程，则u′(x)=1，u(x)=x+C。

第四步:将u(x)代入第二步的y中，得通解为y=e-sinx(x+C)。

解法4——<直接公式法>

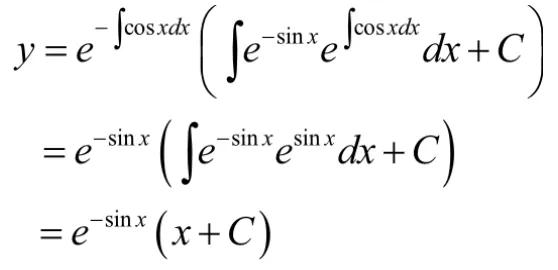
从该例题可以看出:四种方法都能将微分方程的通解求出。公式法虽然看起来简单，但一阶线性非齐次微分方程的通解公式(6)本身比较难记忆，况且数学学科也不主张学生去死记硬背公式。常数变易法和积分因子法、变量变换法步骤均为四步，但常数变易法未能说明一阶线性非齐次和一阶线性齐次的解的联系，学生只知其然，不知其所以然。积分因子法和变量变换法不仅分析了一阶线性非齐次微分方程的解的结构，而且这两种方法的理论并不陌生，均来源于前面所学章节，不仅使学生明白该节知识点，也能与已有知识建立起联系，融会贯通，使知识结构更清晰完整。

3 总结

在教学过程中，应该深入研究教材，查阅相关资料，将理论吃透，严格推导公式，并试图找出多种有效方法去求解，给学生传递更多的理论思想和知识，培养数学思维和素质。