基于改进颗粒簇单元的卸粮宏细观机理模拟

冯 永 原子然

(河南工业大学土木建筑学院,郑州 450001)

自CUNDALL提出离散元法以来，PFC，DEM等基于离散元法的数值模拟软件广泛运用于筒仓领域的研究，并取得了一定的成果[1-3]。筒仓的相关研究中也经常采用PFC中的ball单元来模拟筒仓中的粮食颗粒[4-6]，但是ball单元并不适用于所有实际工程状况,常常存在宏观力学结果与试验结果误差较大、颗粒细观力学参数不全面的情况[7]。产生误差的一个重要原因就是自然条件下的粮食颗粒大多不以规则的形状存在，而传统的单一ball单元模拟不能反映小麦、稻谷等不规则粮食储料的形态差异对卸粮过程中的影响，因此难以准确反映筒仓卸粮过程中的宏细观力学机理，针对这个问题，国内外学者提出clump模型模拟玉米、小麦、煤等颗粒[8-10]，但是对于颗粒形状及含尘率在筒仓卸粮方面对宏细观参数模拟精确度的影响，至今鲜见定量的研究，对于筒仓卸粮实验中含尘率的影响考虑不足[11]。

基于以上分析，本研究提出了一种由clump单元和小型ball单元组成的颗粒簇单元模型，该模型用clump单元模拟粮食颗粒，并添加小型ball单元模拟粉尘颗粒。在推导颗粒之间接触、颗粒-仓壁接触本构关系的基础上[12,13]，以室内卸粮物理模型试验为基础，采用颗粒簇单元模型进行数值模拟试验，并和传统采用单一ball单元的模拟结果进行对比分析。

本研究旨在针对小麦、稻谷等不规则粮食颗粒，建立一种颗粒簇单元模型，更加量化模拟粮食实际形态、含尘率、孔隙率等对卸粮宏细观力学参数影响，客观准确地揭示卸粮过程中的宏细观力学机理，并对类似不规则颗粒的数值模拟也提供参考。

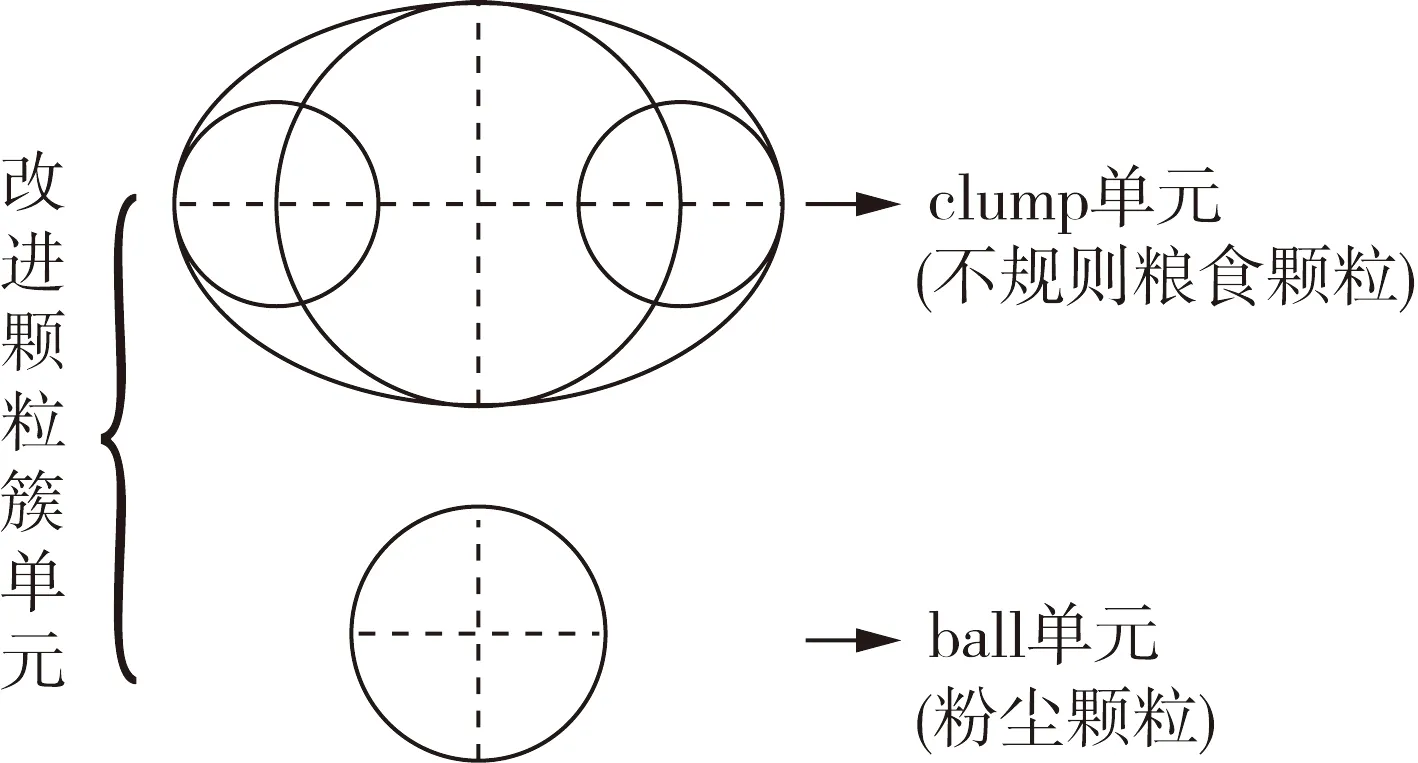
图1 改进颗粒簇单元示意图

1 改进颗粒簇单元的建立

本研究提出的颗粒簇单元由clump单元和传统小型ball单元组成, 该模型用clump单元模拟不规则粮食颗粒，添加小型ball单元模拟粉尘颗粒。

clump是以三个刚性小球相互叠合成一个整体来模拟除刚性圆球外的其他形状。针对本文研究不规则粮食颗粒(小麦、稻谷)的形态，拟合椭圆形状如图1所示。

2 接触本构模型

结合现有研究现状，PFC颗粒基础模型多为线性接触模型[14,15]，根据数值模拟需要，建立相应的力-位移更新公式。

2.1 颗粒单元之间接触模型

将clump单元简化成一个规则的椭圆形，根据力-位移的定律，得到两颗粒接触时的单位矢量模型和颗粒接触变形的情况。认为接触点处的法向切向向量为：

(1)

(2)

两个颗粒相互接触如图2所示。

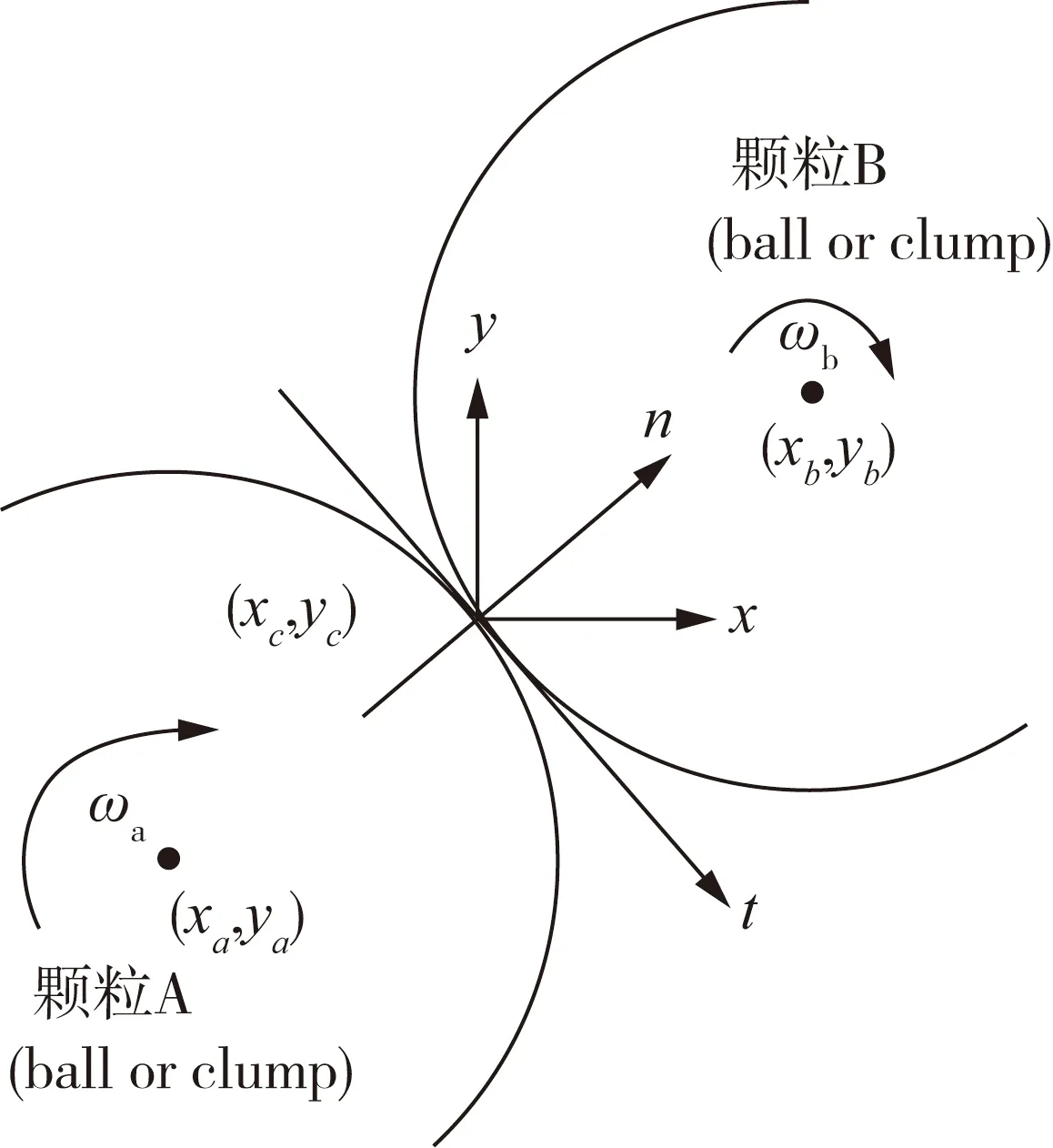
图2 颗粒单元之间接触

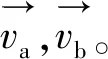
(3)

(4)

则在接触点处两颗粒的相对速度为：

(5)

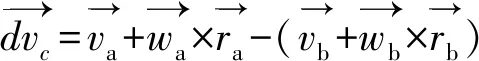
(6)

相对速度在法向和切向的分量如式(7)和式(8)所示。

(7)

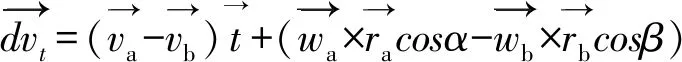
(8)

2.2 颗粒和墙体之间接触

(9)

(10)

(11)

相对速度在法向和切向的分量为：

(12)

(13)

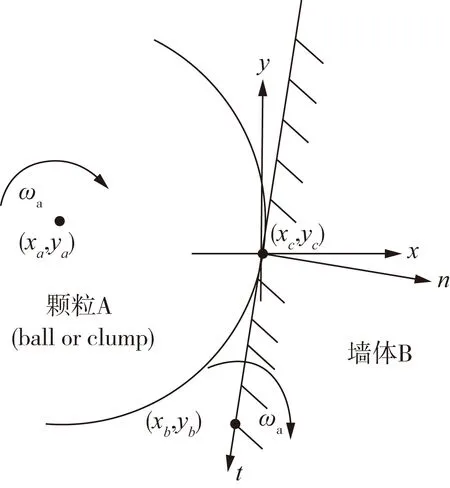
图3 clump单元和墙体之间接触

2.3 力和位移定律

对于颗粒和墙体,法向切向的速度分量都造成了相应方向的位移，根据上述方式所计算出的速度分量，可以得到一个时间段变化的位移分量为Δr，根据力-位移定律[16,17]可以得到单位时间内力的变化量。

(14)

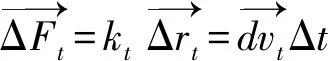
(15)

由此易得颗粒的运动方程：

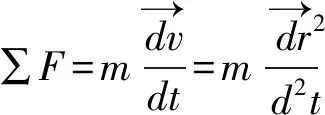
(16)

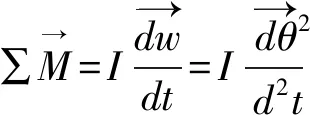
(17)

式中：I为颗粒的惯性矩，∑F为颗粒体所受的合力。

在运算的每个微小时段，细观参数都在发生改变。以颗粒A为例，力在一个微小时段的更新为：

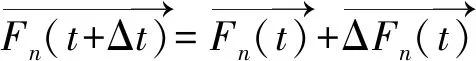
(18)

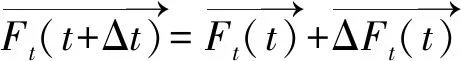
(19)

速度在一个微小时段的更新为：

(20)

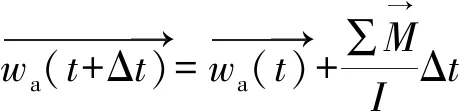
(21)

颗粒位置与旋转角度在一个微小时段的更新为

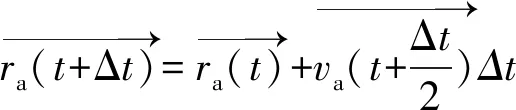
(22)

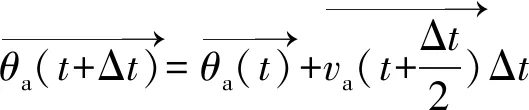
(23)

3 室内物理模型及压力监测点分布

3.1 试验材料

按照实际常用筒仓合理尺寸20 ∶1的缩尺比例制作模型，试验筒仓高1 000 mm，半径250 mm,仓壁厚约5 mm，漏斗半顶角60°。在仓壁布置监测点，每个监测点都布置一个压力感应器来检测筒仓卸粮成拱过程中的侧压力，筒仓模型的具体尺寸和监测点布置由图4所示 。

图4 筒仓模型尺寸和监测点布置

小麦试样选用河南产小麦，小麦长轴粒径分布区间为5～6 mm，短轴粒径分布区间为3～4 mm,试样颗粒尺寸分布比较均匀。

3.2 实验仪器

所选用的压力感应装置为电阻式应变片，型号为B×120-2AA,采集仪器为DH3816N应变测试分析系统。

3.3 试验过程

2018年9月15日进行装粮，将试验模型仓内装满小麦，待装料完成并静置两日后于9月18日撤掉料斗底板进行卸粮。仓壁压力感应器将卸粮过程中仓壁的微小位移通过无氧铜导线输入数据采集系统。

4 数值模拟

4.1 模型建立

根据室内试验的筒仓尺寸，建立一个半径250 mm,高1 000 mm的筒仓模型。用wall单元模拟墙体，用长轴直径6 mm，短轴直径4 mm的clump单元模拟椭圆形小麦颗粒，以10 ∶1的比例添加用直径0.5 mm的ball单元模拟的粉尘颗粒。(原模型储料为直径5 mm的单一ball单元)，单一ball单元模型中所采用的ball单元体积为19.63 mm3，改进颗粒簇模型中的clump单元体积为18.84 mm3，相比降低了4.02%。

在筒仓模型左右两侧遵循试验中监测点的布置分段建立墙体，监控并记录各wall单元的X轴方向所受到的压力，与试验中监测点监测记录侧压力的作用相同。

4.2 参数选取

根据实验室测定以及粮食力学特性[18]选取参数，并通过参数标定[19,20]方法，使静态储粮状态下模拟值与实测值相符合，进一步调整选取参数，最终确定选定的物理力学参数如表 1所示。wall，ball和clump分别表示墙体单元，圆颗粒单元和不规则颗粒单元，kn、ks则分别为它们的法向和切向刚度。

表1 模拟中颗粒和墙体力学参数

墙体和颗粒的线性接触模型所选取的参数如表 2所示。

表2 模拟中主要物性参数

4.3 装粮模拟

根据计算机运算能力和试验条件进行参数取值后，使单一ball单元或改进颗粒簇单元(改进颗粒簇模型为clump单元和小型ball单元，数量比例大约为10 ∶1)以中心装料的方法循环落入筒仓，设定线性接触模型后，颗粒之间将按照第二章的接触模型和更新方式进行运算。

由于如果颗粒内摩擦力较大，则会发生装料缓慢，计算复杂的状况，所以在本研究中采用一种新的装料方法，即在颗粒单元下落过程中不设置颗粒间的摩擦力，待分层装料完成后，用ball property(clump property)命令赋予颗粒体摩擦系数，再迭代一定时步达到稳定。单一ball单元模型装载完成后共含有23 000 个ball单元，堆料高度为0.994 m。改进颗粒簇模型装载完成后含有24 676 个clump单元，2 382个小型ball单元堆料高度为1.013 m。两模型规模相近。

选取左侧点位将模拟所得静态储粮侧压力结果与室内物理模型试验的静态储粮侧压力结果对比(下图5)，结果表示数值相差不大，而整体趋势比较契合，可以验证此模拟试验的真实性。

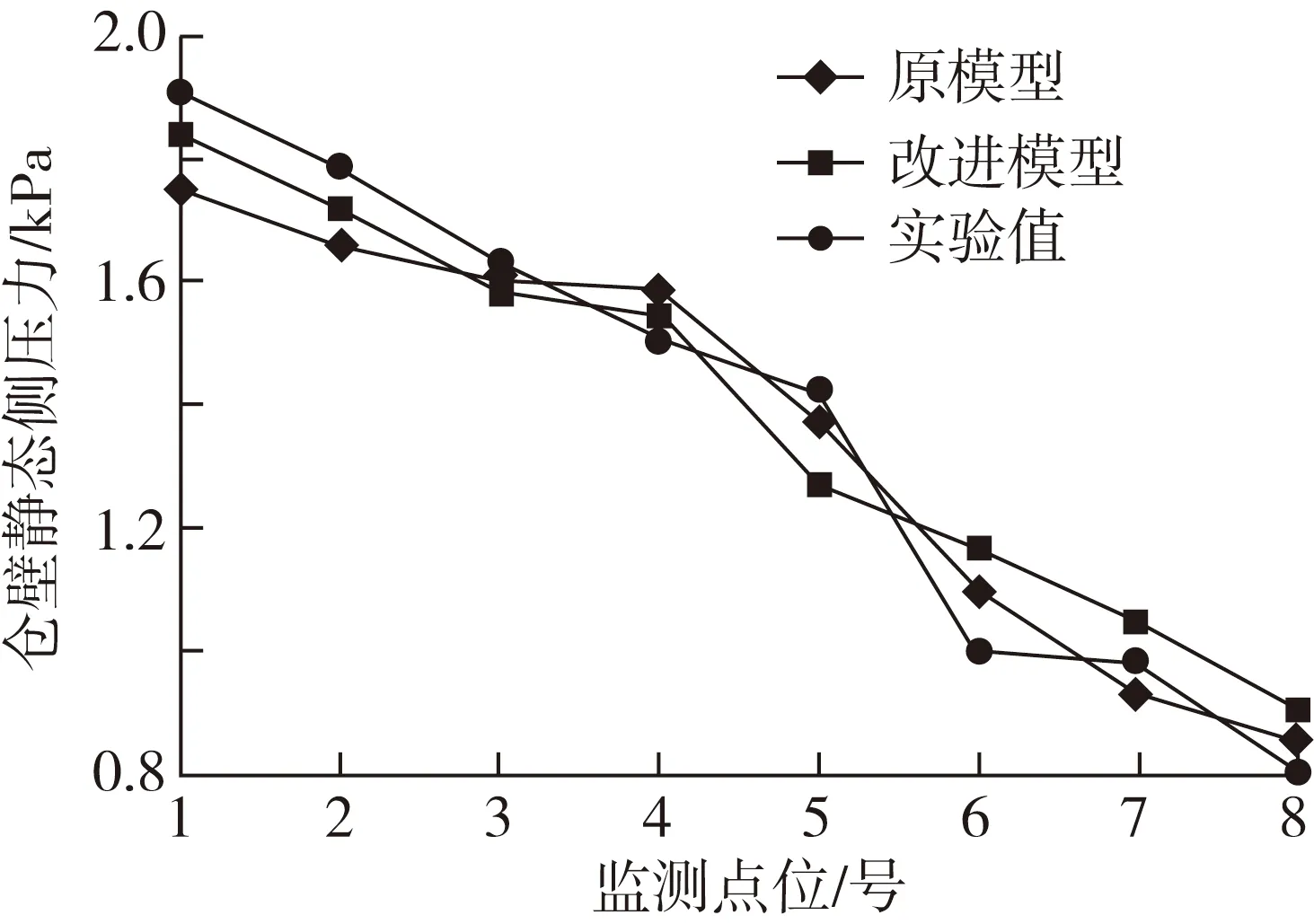
图5 静态装载下仓壁侧压力值

4.4 卸粮动态侧压力模拟对比结果

考虑到上部监测点侧压力波动幅度较小且在卸粮开始一段时间后就进入零压力区而导致不利于观测的问题，选定 1、3、5三个监测点进行卸粮动态侧压力的数据分析。

改进后模型和原单一ball模型在自由卸粮过程中的仓壁动态侧压力如下图6、图7所示。

由图可以发现，在改进前后模型中，动态侧压力均遵循随着深度的降低而减小的原则[21]，改进后模型迭代1 080万步后粮食卸空，对应物理时间为31.4 s,原模型迭代450万步卸空，对应物理时间为29.1 s,改进模型的卸粮过程所迭代的步数较多说明卸粮经历时间比较长，出流相对比较滞涩。

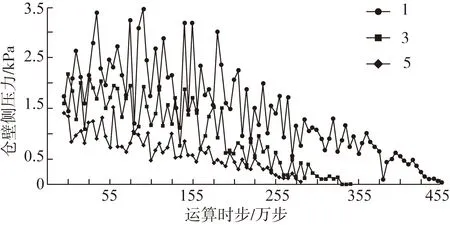
图6 ball单元模型动态侧压力模拟结果

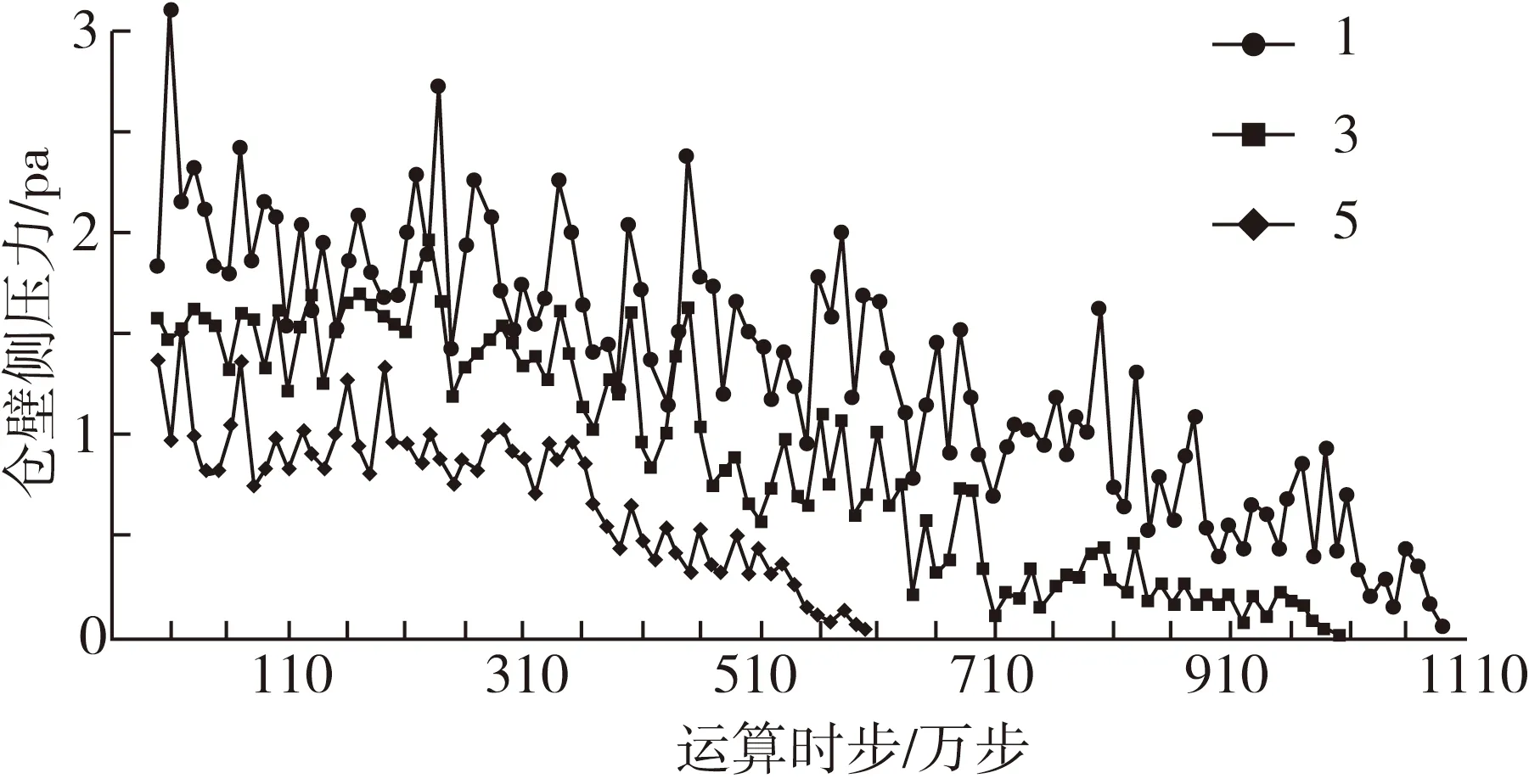
图7 改进颗粒簇模型的动态侧压力模拟结果

取1号监测点为例进行分析，如图8所示，从卸料开始到结束，原模型和改进颗粒簇模型以及室内试验结果的侧压力变化趋势对比。经过对比可以发现，改进前后模型相较试验结果虽然波动都比较剧烈，但是整体趋势基本一致,且数值围绕实验值波动，其他监测点也呈现类似规律，由此可以进一步验证此模拟试验的真实性。改进后模型的动态侧压力波动幅度比较小，波动趋势较为平缓，这与筒仓卸料过程中改进模型相较于原模型摩擦更充分，颗粒之间的“自锁现象”有关。

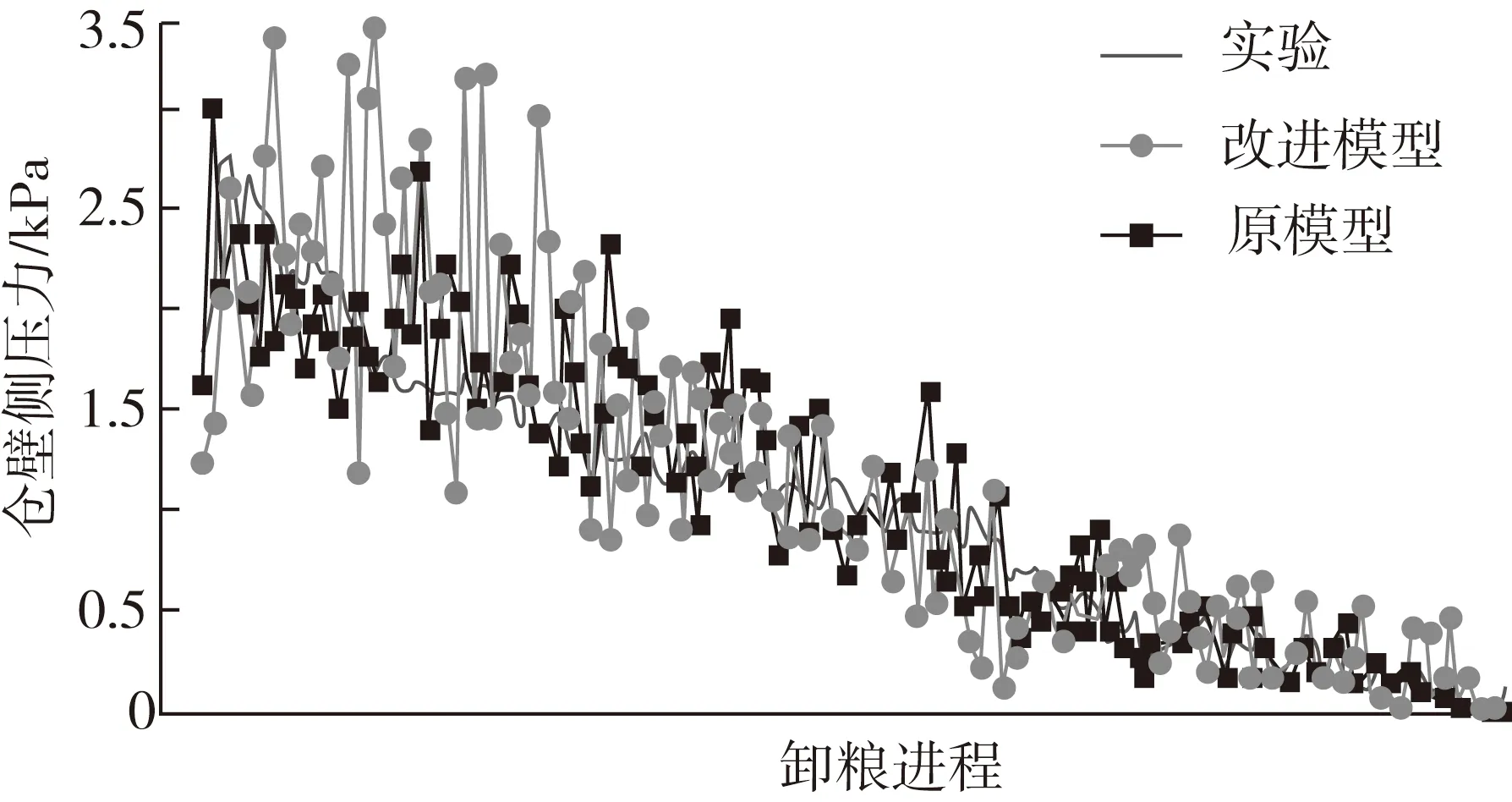
图8 卸料过程中动态侧压力对比

模型误差可以通过公式(24)计算。

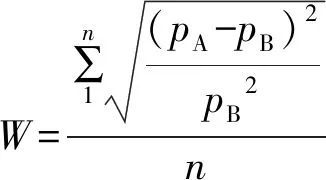
(24)

注：pA为原模型或改进颗粒簇模型的模拟结果；pB为试验结果。

计算可得，改进模型误差为11.28%，原模型误差为29.175%,证明改进模型可以有效地提升卸粮动态侧压力模拟的精确度。各点动态侧压力最大值如表 3所示，可以证明改进模型更符合试验结果。

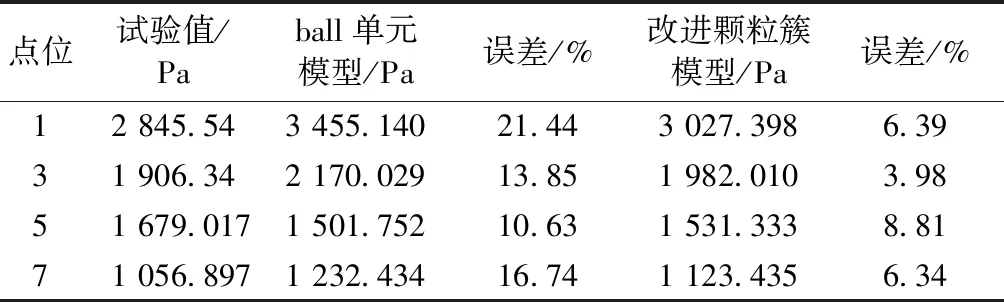
表3 动态侧压力最大值对比

5 细观机理模拟对比分析

以改进模型为例，在筒仓下部建立测量圆，对比改进颗粒簇单元和传统的ball单元的细观结构参数，分析两者细观力学行为。

5.1 细观结构参数对比

利用PFC提供的measure命令生成测量圆[22]，如图9所示。

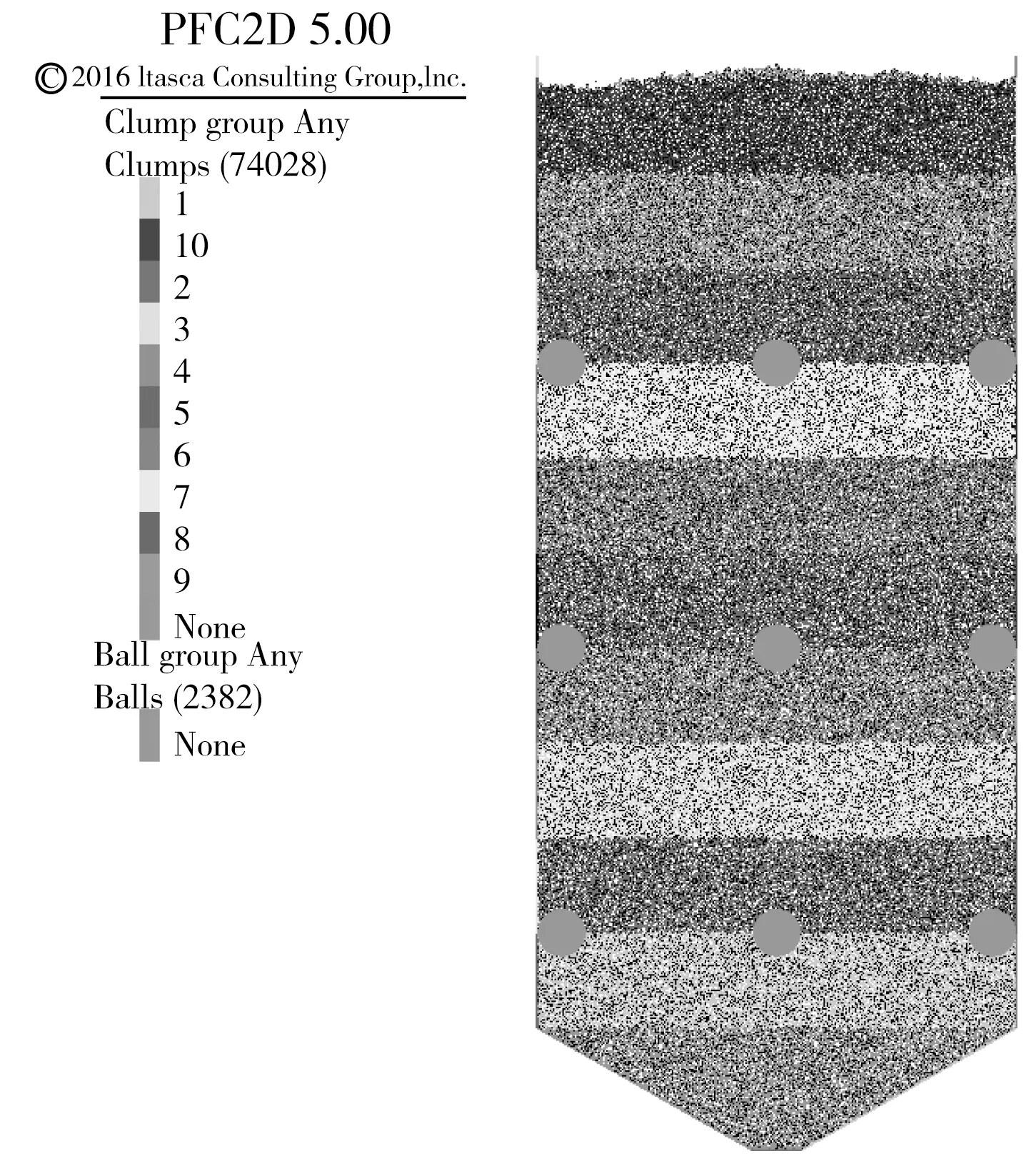
图9 测量圆位置

5.1.1 孔隙率对比

根据孔隙率的定义[23]，可以知道，孔隙率的确定方法为：

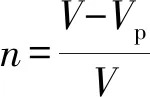
(25)

式中：Vp为筒仓模型中颗粒的体积;V为模型中筒仓区域的体积。可以得到圆球颗粒和椭圆颗粒计算体积的表达式为：

Vpb=nb×R2π

(26)

Vpc=nc×(Ra×Rb×π)

(27)

则原单一圆球颗粒模型的孔隙率表达式为：

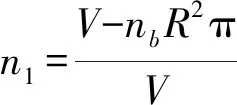
(28)

改进后模型孔隙率表达式为：

(29)

筒仓在静态储粮状态下，根据室内试验结果，小麦在粮仓储存状态下，孔隙率为40.04%，观测模型中九个measure圆的平均孔隙率，本研究选用2D模型，由孔隙率转换关系[24]：

ε3d=1-ξ(1-ε2d)

(30)

(31)

式中：Dr为粮食相对密实度；ε2d为粮食二维孔隙率；ε3d为粮食三维孔隙率。

计算可得转换得到三维状态下的改进颗粒簇模型孔隙率为39.13%，误差2.27%，而单一ball单元模型孔隙率为42.20%，误差5.39%。改进模型在储粮孔隙率方面下降了3.07%，储料更加密实，精确度提升了3.12%。

5.1.2 配位数对比分析

配位数也是重要的细观结构参数之一，与孔隙率一样用以表征堆积颗粒的密实度，意为某一颗粒附近与颗粒相接触的颗粒数量，配位数与孔隙率成反比[25]。原模型配位数为3.67，改进后模型配位数为4.66，证明改进模型可以有效增大颗粒集合的配位数。在细观结构参数方面，改进模型可以使粮食更密集。

5.2 细观力学行为对比分析

通过对比两种模型下的卸粮力链图，比较分析其细观力学动态变化，根据所得结果可以清晰地发现，原模型接触力数量为31 279，改进后模型的接触力数目为61 403，可以得知改进后模型的力链更加密集，颗粒间的结构网络更加复杂。根据图10所示的两模型局部力链图，改进后模型的力链更密集，接触力分布更均匀。由于颗粒的自锁现象[26]，clump单元之间易形成坚实的颗粒链抵御外力作用。改进的颗粒簇单元模型中可以清晰地看到数条横向的拱形力链，更加符合卸粮中瞬时拱此消彼长的实际情况[27]。

图10 卸粮模拟力链图

6 结论

以室内卸粮物理模型试验为基础，采用改进颗粒簇单元进行数值模拟试验，并和传统采用单一ball单元的模拟结果进行对比分析。研究表明颗粒形态不仅影响筒仓卸粮过程中的宏观力学行为，对颗粒间的细观结构，流动过程中颗粒间的力链动态演化过程都有明显影响。

从宏观角度来看，改进颗粒簇模型使得仓壁卸粮动态侧压力波动更平缓，卸粮过程持续时间更长。通过对比模拟与试验卸粮过程中所得动态侧压力结果，改进模型误差为11.28%，原模型误差为29.175%,改进颗粒簇模型相比原模型降低了17.895%的误差。

颗粒细观结构方面，筒仓在静态储粮状态下，原模型孔隙率为42.20%，而改进模型孔隙率为39.13%，改进模型的颗粒堆积孔隙率下降了3.07%，精确度上升了3.12%，原模型配位数为3.67，改进后模型配位数为4.66，配位数增大了27%，说明改进颗粒簇模型可以有效地增大颗粒堆积的密实度，更符合实际粮食颗粒接触情况。

粮食颗粒形态影响颗粒的细观力学行为，模拟结果表明改进模型接触力数量和传统ball模型相比增加了30124，接触力链分布更均匀密集，改进的颗粒簇单元模型中可以清晰地看到数条横向的拱形力链，更能清晰反映出瞬时拱此消彼长的动态变化规律。

针对筒仓卸粮方面的改进颗粒簇模型，有效提高了模拟的精确度，不仅对日后粮仓的设计提供了参考，而且对于进一步模拟不规则粮食颗粒在仓内的流动机理也具有重要借鉴价值。