Application of Mode Synthesis Method for Vibration Analysis of Geometrically Mistuned Bladed Disk Considering the Prestress*

(College of Aerospace Engineering,Chongqing University)

Abstract：The importance of mistuning analysis lies on understanding the vibration characteristics of the bladed disk.Previous works generally ignored the nonlinear effect of prestress,which increase the gap between the actual results and research results. In this paper, a unique way to address the reduced-order model is presented, where disk and each blade component is attached as individual substructures with free-interface component mode synthesis considering prestress.The influence of nonlinear inertial effect on mistuning characteristics of rotors is compared with linear inertial effect. Results show that ignoring nonlinearity of the rotational speed, the influence of speed on mode localization may be different from the true situation.

Keywords：Mistuned Bladed Disk,Pressed Component Mode Synthesis,Free-interface,Mode Localization,Nonlinear Inertial Effect

0 Introduction

Theoretically,the bladed disk of aero-engine has characteristics as cyclic symmetry.Due to the scattered properties of materials,the small imperfections in manufacturing,uneven wear and intentionally detuning frequency,the practical blades have small difference from each other,which is called mistuning.The impact of mistuning on structural response is disproportionate geometric size and generate forced response amplitude magnifications severe enough to instigate high cycle fatigue failure(Castanier&Pierre,2006)[1].In order to predict the vibratory response characteristics of industrial bladed disks,it is necessary to quantify the effects of mistuning.

Much research has been done on the dynamic behavior of mistuned bladed disks,and many of these studies have been based on the approaches called proportional mistuning(Lim,2003)[2],which change the materials properties of blades to simulate the mistuning(Bladh,2002)[3].These methods assume that the quantity of mistuning is proportional to the mass or stiffness matrix of tuned blisk and only blade natural frequencies are changed without impacting the corresponding mode shapes.Proportional mistuning do provide a basic understanding of the effects of mistuning and has been shown to work well(Yao,2016)[4].However,the proportional mistuning might not be completely consistent with the true situation.Many research results indicate that compared to proportional mistuning,change of geometry of blades to simulate the mistuning,considering both frequency and mode shape variation,is closer to the practical situation and yields significantly better predictions of vibration characteristics(Beck,2013)[5].Thus,this paper focuses on the vibration characteristics of geometric mistuned bladed disk.

On the other hand,because of mistuning,the analysis of cyclic symmetry and adopting a single sector of tuned bladed disks cannot be used to analyze mistuning blisks.Although it is quite possible to model the full bladed rotor in software,because of the stochastic nature of mistuning,Monte Carlo simulations must be conducted to determine the statistics of response,the cost of which would be prohibitive if using finite-element models of full rotors(Sihan&Bhartiya,2011)[6].Therefore,various techniques have been developed to construct reduced-order models(ROM)of bladed disks systematically from their finite element representations.Many of these techniques built ROMs by substructuring the bladed disk into disk and blade components,which allows for easy implementation of blade mistuning.And the component mode synthesis(CMS)techniques are popularly used for combining substructures in structural dynamic applications.Hurty(1965)[7]first proposed the method of CMS,which was improved by Craig and Bampton(1968)[8].This method is known popularly as the fixed-interface CMS method(also called C-B CMS).Based on C-B CMS,much research has been done on the geometric mistuned bladed disk(Marinescu,2011;Beck,2014)[9-10].However,Beck et al.(2014)[10]pointed out that a drawback of C-B CMS was the retention of all DOFs at the component or substructure interfaces,which made the DOFs hard to be reduced.With number of blades increasing,the size of interface DOFs may be too large to ignore and finally decreases the efficiency of C-B CMS.To overcome the shortcoming,free-interface CMS was proposed(Macneal,1971)[11],which removes all the boundary or interface degrees of freedom(DOFs)after the synthesis and reduces even further the parent finite element model.The research of Salas et al.(2017)[12]shows that free-interface CMS can get satisfactory results of geometric mistuned bladed disk vibration analysis with more ROM size reduced than C-B CMS.Therefore,the free-interface CMS is utilized in this article.

Furthermore,inertial effects on bladed components are necessary for accurately prediction of vibration characteristics of rotors.Marugabandhu and Griffin(2000)[13]evaluated the effect of rotational speed on the natural frequencies and mode shapes of blades by a linear combination of modes.Sternchüss and Balmes(2006)[14]proposed a ROM with a linear approximation of centrifugal effect,which provided an accurate representation.However,because it relies on a linear finite element model which ignore the nonlinearity,not only the deformation of blades but also the stress distribution of blisks may be different from the actual results(Batailly and Millecamps,2016)[15].The stress distribution obtained by the nonlinear structural simulation of rotating blisk is called nonlinear prestress.Khalifeh et al.(2017)[16]suggested that ignoring the nonlinear inertial effect may fail to provide accurate predictions of vibration of bladed disk.In this paper,the influence of nonlinear effect of rotational speed on mistuned rotor is studied.

This paper is organized as follows.We first introduce the method of free-interface CMS and verify the accuracy and efficiency of the method on analysis of a geometrically mistuned blisk.Then,the influence of rotation speed on the vibration characteristics of the mistuned rotor is investigated.Finally,conclusions from this study are summarized.

1 Dynamics Modeling of The Prestressed Component Mode Synthesis Method

Superelement method of mode synthesis is a kind of dynamic reduce order method,which is generally adopted for dynamic analysis of the mistuned bladed disk.The basic idea is dividing the whole structure into several substructures and each substructure can be generated to a superelement by free-interface mode synthesis method(Hintz,1975;Herting,1985)[17-18],which could reduce the number of degrees of freedom.

The general non-damping vibration equation of the substructure in the finite element model can be expressed as

in which[m]and[k]are the mass and the stiffness matrix,respectively,{f}is the force of the substructure,and{x}is the displacement vector.Because of the centrifugal force,the stress state of the bladed disk will change.Considering the influence of centrifugal effect on dynamic characteristics of the rotor,the new equation can be given as

in which[k']is the stiffness matrix after considering the prestress.

The total DOFs can be divided into the master DOFs on the interface and the slave DOFs on the interior,respectively.Therefore,Eq.(2)can be written as

in which subscriptiandjdenotes the master DOF and slave DOF,respectively.fiis the force on the interface andfjis the force on the interior.Furthermore,free-interface mode synthesis method assume that the DOF on the interface are totally free.

Solving the Eq.(2)can get the firstkth the frequencyωkand normal mode[φk]of each substructure with free-interface,which is the master modes set,while the high order residual mode set denoted as[ψd].Then the coordinate transformation equation of the substructure can be written as

in which{p}represents the modal coordinate.Eq.(2)can be rewritten as

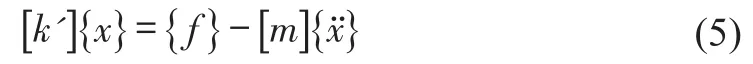
Ignoring the influence of inertia force and only considering the contribution of elastic force,first-order approximation of Eq.(5)can be obtained as

which also can be written as

Using the weighted orthogonality of the modal matrix and the stiffness matrix,we can get the following,

in which

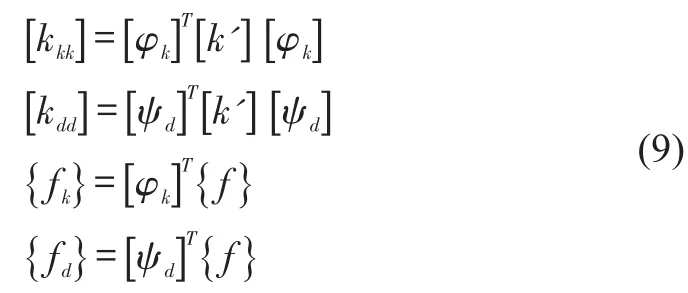
Combining the Eq.(4)and Eq.(8)will get

Transforming Eq.(9)into Eq.(10)leads to

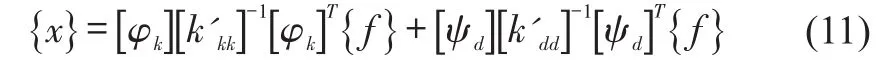
which also can be written as

The residual compliance matrix can be gotten by coupling Eq.(6)and Eq.(12)

in which[G]=[k]-1.

In consideration of the free vibration equation of the system,dividing the Eq.(12)by the master and slave DOF and combining it with Eq.(6)will lead to

So the master and slave physical coordinate of the substructure can be expressed as

Coupling the above two equations can get

then

Thus,the reduced mass matrix,stiffness matrix and force vector can be written as

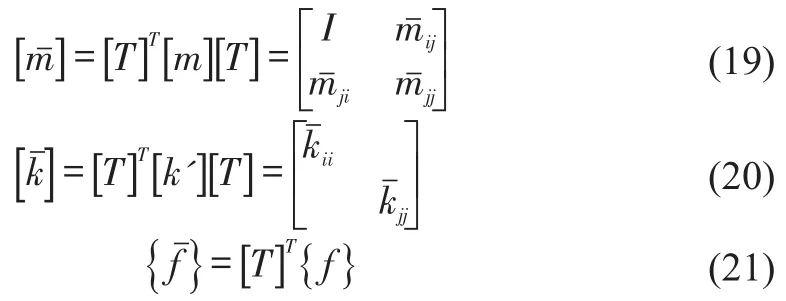
The reduced order model of substructure is obtained and the superelement of substructure is generated.

The motion Eq.(2)of the physical coordinates can be transformed into the motion equation of the mode coordinate.

The motion equation of each substructure mode coordinate that was obtained from Eq.(22)can be assembled.

It is assumed that the rigid connection of interface,which contains the displacement coordination conditions

and the balance conditions of force

Therefore,the general coordinate of system is

Therefore,Eq.(23)can be transformed to the general coordinate by Eq.(27)

in which

This is the reduced vibration equation of the assembled superelements.The natural frequency and mode shape of general coordinates can be obtained by Eq.(28).The mode shape of general coordinates can be transformed to physical coordinates using Eq.(27)and Eq.(18).

2 Modal Analysis of the Geometric Mistuned Bladed Disk

2.1 The Analysis Process of Mode Synthesis Method

Mode synthesis method is an effective means for analyzing the complex structure.First,divide the total structure into several substructures.In this paper,each blade and the corresponding disk are used as a substructure.Then,use modal analysis to reduce the substructures and get superelements.Finally,assemble the superelements and get the reduced-order model to obtain the vibration characteristics of the whole blisk.The flow chart is shown as Fig.1.

Fig.1 The Flow chart of Mode Synthesis Method of Bladed Disk

2.2 The Finite Element Model of the Substructures of Bladed Disk

A model of aero-engine compressor bladed disk with 48 blades is taken as an example (shown as Fig.2.The finite element model has 175 392 nodes and 128 160 elements.The inner surface of disk is fixed.The material parameters of the model are listed as follow.Elasticity modulus is 1.09×1011Pa;Poisson's ratio is 0.34;density is.To simulate the geometric mistuned bladed disk of which the rotational speed is10 000r/min,the thickness of each bladed is changed randomly between±3%.

Fig.2 The Model of Bladed Disk with 48 Blades

Tuned Analysis

The purpose of a tuned analysis is to compare the new ROM method with free-interface CMS approach against the general finite element method(FEM).The accuracy of the ROM method depends on how many of modes of per superelement are retained and used in the reduction.In this paper,the first 40 order modes of disk and first 60 order modes of each blade are kept.The frequencies for the parent tuned bladed disk whose rotational speed is10 000r/minare visualized against nodal diameters(NDs)in Fig.3.

As stated in Bladh(2001)[19],an important way for the blades without shrouds to communicate with one another is through the disk.For this reason,the interblade coupling is highly affected by the interaction of the disk-and blade-dominated modes.These modal interactions are known as veering regions and are observed in Fig.3 as a deviation of the disk and blade modes’frequency.Some of veering regions have been marked.

Mistuned Analysis

After understanding the accuracy for Free-interface CMS method in spanning properly the disk and blade modes of a tuned blisk,a detailed analysis with respect to a geometric mistuning has been assessed.Mistuning frequencies is not possible to be addressed as a function of the ND because mistuning breaks the traveling waves inherent of a tuned blisk,which means that all the mode shapes are considered unique.Thus,the frequencies have to be arranged in increasing order.The mode families are more difficult to identify,but still possible as observed in Fig.4(a)(linear prestress)and Fig.5(a)(nonlinear prestress).

As observed from Fig.5(b)and Fig.6(b),the relative errors of all normal frequencies are less than3×10-3%and there clear visualizations of the relative error increasing when it goes into the veering regions,which is still in the acceptable range.Another important parameter to study is the relative error of maximal displacement of the eigenvector for linear prestress and nonlinear prestress cases as shown in Fig.7.The curves in two figures have the same trend,the relative error in veering regions has a significant increase and the value becomes larger with frequency.

3 Influence of Prestress on the Characteristics of the Geometric Mistuned Bladed Disk

3.1 Definition of Mode Localization Factor

The difference between the mistuned and tuned mode shapes is generally described by mode localization factor(MLF).Wang et al.(2008)[20]gave the definition of MLF based on the nondimensional maximal displacementuof the sub-eigenvectorΦ,anduis defined as

Fig.3 Tuned Frequencies vs Nodal Diameters

Fig.4 Model Analysis of the Geometric Mistuned Bladed Disk Considering Linear Prestress

Fig.5 Model Analysis of the Geometric Mistuned Bladed Disk Considering Nonlinear Prestress

Fig.6 Relative Error of Maximal Displacement of the Eigenvectors

Fig.7 MLFs of Mistuned Bladed Disk with Linear Prestress

urepresents the ratio of the maximal vibration amplitude and the sum of the vibration amplitudes of all blades,so the largeruis,the more severe the mode is localized in a single blades.The influence of the mistuning can be expressed as

in whichumandunare the nondimensional maximal displacements for the mistuned and corresponding tuned mode shape.

3.2 Influence of prestress on mode localization factor

To analysis the rotation speed on the characteristics of geometric mistuned bladed disk,the first 100 order modes of the above model at different rotate speeds were calculated by free-interface CMS method and the influence of linear prestress and nonlinear prestress are considered respectively.The variation of MLFs in different situations and the changing trend of maximal MLF are showed in Fig.7(linear prestress)and Fig.8(nonlinear prestress).

As shown in Fig.7,in the case of considering linear prestress,the rotation speed hardly influences MLF.However,if nonlinear effect is considered,the influence of rotational speed will be apparent,especially in the higher order modes.

It is clearly shown in Fig.7 and Fig.8 that at different rotational speeds,no matter whether the nonlinear effect is considered,the maximal MLF occurs in the 48thorder mode,which located in a veering region.As Óttarsson and Pierre(1995)[21]have pointed out,a moderately weak coupling has a major effect in the vibration characteristics of the blisk in which the energy concentrates in few blades,which means that the MLFs of the modes in veering regions are more sensitive to mistuning.

Furthermore,it can be observed from Fig.7(a)that the maximal MLF increases with the speed while an opposite trend is shown inn Fig.8(a).To study the influence of speed,another three random mistuned bladed disks are added and the maximal MLFs of them in different rotational speeds are shown in Fig.9.It suggests that ignoring the nonlinear influence of rotation speed and only considered the linear inertial effect,the prediction of geometric mistuned bladed disk may be not exact.

Fig.8 MLFs of Mistuned Bladed Disk with Nonlinear Prestress

Fig.9 Maximal MLFs in Different Rotational Speeds of Different Mistuned Bladed Disk

4 Conclusions

The model analysis of a geometric mistuned bladed disk has been performed using free-interface component mode synthesis considering prestress.Both linear and nonlinear situation are taken into account.The analyses are performed on a practical blisk,not only focusing on its normal model,but also understanding the accuracy of the noncyclic reduced-order models(ROMs)within the blisk’s nodal diameter spectrum.This method shows satisfactory accuracy when compare to a parent finite element model.A comparison between the influence of linear prestress and nonlinear prestress has been completed for a geometric case,and results have showed different influence of the rotation speed on the mistuned blisk,which indicates that in some situations,only considering the linear effect of rotation may not obtain the true prediction of the mistuned bladed disk.