多级低滞后型刷式密封流动传热特性数值研究*

2019-11-14

风机技术 2019年5期

（沈阳航空航天大学航空发动机学院辽宁省航空推进系统先进测试技术重点实验室）

0 引言

刷式密封是广泛应用于透平机械中的优良接触式密封[1]。由于单级刷式密封承压能力有限，目前已很难满足透平机械的实际需求，因此采用多级刷式密封替代单级刷式密封可以有效的解决单级刷式密封承压问题，由于传统两级刷式密封第二级的实际承压要大于第一级承压，这就造成了两级级间压力不均衡性，严重影响了其使用寿命。在实际工作中，转子高速运转时，刷丝与转子摩擦产生大量的热，当温度过高时会出现刷丝熔断现象，这也将使密封性能和使用寿命大大降低。目前对多级刷式密封的级间压力均衡性和传热特性研究的文献鲜有发表，因此开展多级低滞后型刷式密封的级间压力均衡性和传热特性研究具有重要的意义[2]。

对于单级刷式密封的流场分布特性和传热特性已有学者进行了大量研究[3-11]。Hendricks R C等[12]通过实验研究了两级刷式密封的压力分布情况，研究结果表明，两级刷式密封存在级间不平衡性，并且第一级的压降约为总压降的40%，第二级为60%；Pugachev A O等[13]通过实验测得了刷式密封腔内的周向压力分布特性和刚度系数，建立了多级刷式密封多孔介质模型，结果表明，与迷宫密封相比，刷式密封可降低60%左右的泄漏量，且具有正直接刚度和较小的交叉耦合刚度。邱波等[14]运用实验和Non-Darcian多孔介质数值方法研究了两级刷式密封的泄漏流动特性，研究结果表明，两级刷式密封的泄漏量随着压比和密封间隙的增大而增大，随着转速的增大而减少。文龙和王之栎等[15]采用多孔介质模型和有限元法分析了双级低滞后刷式密封级间不均匀性，研究结果表明，增大第一级刷丝的安装角和减少第二级的安装角，可以使两级分压区域均衡，改变第二级的前板间隙高度对级间不均衡性影响不大，当背板间隙高度一定时，两级可达到均衡。王凯杰，杨义勇等[16]建立了二维叉排管束模型，分析了两级刷式密封的压力和流速的分布规律以及不同结构参数对压力和流速的影响规律，研究结果表明，当上下级排数相同时，下游承受的压降大于上游，随着压力的增大，级间不均匀性增大，当级数大于三级时，泄漏量基本不再减少，可通过增加上游级排数和减少下游级排数来改善压力不均匀性。文龙，王之栎[17]运用热对流和热传导方法对温度场进行数值计算，研究结果表明，随着压比的增大，温度场发生变化，最高温度升高，低压级刷丝尖端温度大于高压级刷丝尖端温度。综上，目前对多级刷式密封的级间压力分布特性和传热特性研究较少，且大多基于多孔介质模型，未考虑刷式密封三维实体模型，鲜有文献基于三维实体模型对多级刷式密封级间压力分布特性与传热特性的研究成果报道。

本文建立了多级低滞后型刷式密封三维实体传热求解模型，在验证模型准确性的基础上，分析了两级和三级低滞后型刷式密封在不同压比条件下的级间压力分布特性，温度分布特性和刷丝的热变形特性，最后揭示了多级刷式密封的传热规律。

1 刷式密封传热特性理论分析

1.1 摩擦热量的计算

刷式密封是具有优良密封性能的接触式动密封，为保证刷式密封能够适应转子的瞬间径向变形或偏心运动而保持良好的密封性能，刷丝束在安装时沿着转子旋转方向存在着一定的周向倾角排列，以保证刷式密封的密封性能。实际工作中刷丝束与转子之间会发生摩擦产生大量的热量，影响着刷式密封的密封性能。

摩擦热量Q的大小决定了刷式密封温度的高低，Q主要由刷丝束与转轴之间的摩擦系数、刷丝束与转轴的法向接触力以及刷丝束与转轴表面的相对线速度决定，计算公式为：

式中，Ff为刷丝束与转轴之间的摩擦力；μ为摩擦系数，本文取0.3[18]；Fn是刷丝束与转轴的法向接触力；v是刷丝束与转轴表面的线速度。

刷丝束与转轴的法向接触力由刷丝束与转轴直径的干涉量和刷丝束刚度有关[18,19]，计算公式为：

式中，Δr为刷丝束与转轴之间的干涉量，γBTP为刷丝束刚度，即刷丝在气流力作用下抵抗弹性变形的能力。

1.2 刷式密封三维传热理论计算模型

1.2.1 流动控制方程

刷式密封三维传热特性计算时，流体域满足动量方程和连续方程[20-21]：

其中，ρ为密度；t为时间；P为流体微元体上的压力；U为速度矢量；u，v，w为速度矢量U在x，y，z方向的分量；Г为平均有效扩散率；Su，Sv，Sw为动量守恒方程的广义源项，即：

式中，Fx，Fy，Fz为流体微元体上的体力，若体力只有重力，且z轴竖直向上，则Fx=0，Fy=0，Fz=-ρg；μ为动力黏度。

刷丝束区域流场流动复杂，流场的湍流度和黏性系数体现出各项异性，需要对标准k-ε湍流模型进行修正，修正模型RNGk-ε模型为：

采用理想气体作为空气介质，因此满足理想气体状态方程：

其中，M为摩尔质量常数，R为理想气体常数。

1.2.2 传热控制方程

空气的黏性系数与温度的变化关系为：

式中，μ0=1.716×10-5kg/(m·s)；S=116K；T0=273K。

采用理想气体进行计算，流体求解温度的控制方程为：

式中，div为散度算符；ρa为空气密度；u，v，w分别为x，y，z方向的流速；U为速度矢量；T为温度；p为流体压力；τ为切应力；e为能量；Ka为空气导热系数。

刷丝的材料为Haynes25，其稳态的传热控制方程为：

也可以表示为：

式中，tw为固体表面温度；t∞为流体表面温度；Δt=tw-t∞。将式（10）代入坐标系坐标可得到流固换热微分方程：

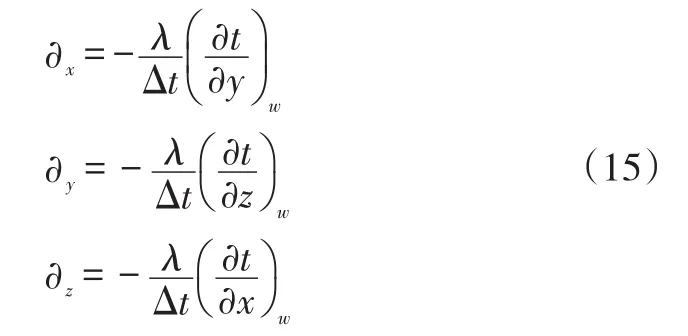
2 刷式密封流场特性数值模型

2.1 求解模型

本文以多级低滞后型刷式密封为研究对象，由于刷式密封整周建模计算量较大，为提高计算效率，本文以最小循环单元建立刷式密封三维实体传热求解模型。其中两级低滞后刷式密封结构示意图如图1所示，刷丝材料为Haynes25，弹性模量为213.7GPa，泊松比为0.29，比热容为385.204J/(kg·K)。刷式密封的主要几何尺寸如表1所示。

图1 刷式密封二维结构示意图Fig.1 Brush seal 2D structure diagram

表1 刷式密封件主要几何尺寸Tab.1 Brush seal main geometry

2.2 网格划分

进行网格划分时，考虑到刷式密封的流动特性，采用混合网格划分方法，对刷丝束区域采用四面体网格，刷丝采用边界层网格，由于刷丝区域内部流动较为复杂，为得到准确的刷丝束内部流动情况，对刷丝束区域进行网格加密处理。刷丝区域以外的流体区域均采用规则的六面体网格，以提高计算速度和精度。由于网格质量对温度求解结果影响较大，进行网格无关性验证后，最终确定流体域网格数为320万，固体网格为24万。两级低滞后刷式密封网格划分如图2所示。

图2 网格划分示意图Fig.2 Meshing

2.3 边界条件

图3给出了两级低滞后刷式密封边界条件示意图。主要包括：进出口均采用压力边界条件，转子面采用无滑移边界条件，考虑到刷式密封的周向对称性，设周期性边界条件，刷丝束与流体接触区域采用对流换热耦合面边界条件，刷丝束与流体之间的对流换热通过此边界完成，另外考虑到在实际工作中，摩擦热量主要是通过刷丝自由端与转子面之间摩擦产生大量的热量，因此刷丝自由端面设置为摩擦热流量边界条件，将刷丝束区域不同的产热量视为相同，在计算时假设有一半的热量传递至刷丝束[2]。

图3 刷式密封模型边界条件示意图Fig.3 Brush seal model boundary condition

2.4 模型准确性验证

本文进行模型准确性验证时，选取文献[2]进行求解模型准确性验证，如图4所示。由图4可以看出，随着压比增大，本文计算的泄漏量与文献[2]中的泄漏量均不断增大，且两者吻合较好，在所计算的压比范围内，两者的最大误差不超过10%。另外还给出了在热流密度为1 000kW/m2时，不同压比条件下本文计算得到的最高温度与文献[2]最高温度对比曲线，可以看出在给定热流密度条件下，随着压比增大，两曲线逐渐降低，且两者吻合较好，两者的最高温度最大误差不超过15%。偏差出现的原因主要是因为本文基于三维实体建模，考虑了刷丝与刷丝之间的流动传热情况，而传统的多孔介质模型是通过改变孔隙率来改变刷丝束疏密程度，未考虑实体模型，因此出现了计算偏差。从泄漏量和最高温度的对比验证结果可以看出，文献[2]中的计算结果与本文的计算结果吻合较好，从而验证了本文求解模型的准确性。

图4 泄漏量、最高温度与文献对比验证Fig.4 Comparation of leakage,maximum temperature with literature

3 刷式密封流场和温度场分布特性分析

3.1 级间压力分布特性分析

图5和图6分别给出了当压比为3时，两级和三级低滞后型刷式密封的压力分布云图。由图可以看出，两种结构刷式密封均进口出压力最高，经过刷丝束压力逐级递减，压降在末级刷丝束区域最明显。在相同压比条件下，两级低滞后型刷式密封第二级压降较大，三级低滞后刷式密封第三级压降较大，两种结构刷式密封的最大压降均出现在末级刷丝，此外，刷丝束区域的轴向压差和径向压差均逐级增大，轴向压差是影响刷丝“滞后效应”的关键因素，径向压差是影响“吹下效应”的关键因素，因此，两种刷式密封结构的末级刷丝均最容易发生“滞后效应”和“吹下效应”。

图5 两级低滞后型刷式密封压力分布Fig.5 Distribution of two-stage low hysteresis brush seal pressure

图6 三级低滞后型刷式密封压力分布Fig.6 Distribution of three-stage low hysteresis brush sealing pressure

图7和图8分别给出了两级和三级低滞后型刷式密封在不同压比条件下，每级出口处的平均压力值变化规律，两种刷式密封结构的每级的压降变化情况可通过折线斜率判断，可以看出两种形式刷式密封压降逐级增大，随着压比的增大，每级压降随之增大。为更直观的看出不同压比条件下，每级压降的占比情况，绘制的柱形图如图9和图10所示，可以看出，当压比为2时，两级低滞后型刷式密封第一级压降占总压降40%，第二级压降占60%，随着压比的增大，第一级刷丝束承压逐渐减小，第二级承压逐渐增大，当压比达到5时，第二级压降占67.2%，第一级压降占32.8%；三级低滞后型刷式密封在压比为2时，第一级压降占27.8%，第二级压降占30.2%，第三级压降占42%，随着压比的增大，第一级和第二级承压逐渐减小，第三级承压逐渐增大，当压比达到5时，第一级压降占19%，第二级压降占26.5%，第三级压降占54.5%。综上，两级和三级低滞后型刷式密封结构在不同压比条件下，刷丝压降占总压降比例逐级增大，且末级承压最大，随着压比的增大，末级刷丝压降逐渐增大，占总压降比例变化不明显，而在相同压比条件下，三级低滞后型的末级压降占比要低于两级低滞后型的末级压降占比。因此，实际工作中，末级刷丝承压较大，较易发生损坏，从而使得密封性能降低。

图7 两级低滞后型刷式密封每级出口压力变化规律Fig.7 Two-stage low hysteresis brush seal change law of outlet pressure per stage

图8 三级低滞后型刷式密封每级出口压力变化规律Fig.8 The change law of outlet pressure per stage for the three-stage low hysteresis brush seal

图9 两级低滞后型刷式密封不同压比时每级压降占比Fig.9 Pressure ratio percentage per stage under different pressure ratio for the two-stage low hysteresis brush seal

图10 三级低滞后型刷式密封不同压比时每级压降占比Fig.10 Pressure ratio percentage per stage under different pressure ratio for the three-stage low hysteresis brush seal

3.2 速度分布特性分析

图11和图12分别给出了在压比为3条件下，两级和三级低滞后型刷式密封结构的速度矢量图。由图可以看出，两种刷式密封结构上游区速度较稳定，经过第一级刷丝束速度逐渐增大，经过第二级刷丝束速度达到最大，最大速度发生在二级刷丝末排刷丝自由端靠近后挡板位置，这是因为在此位置轴向速度与径向速度汇合，最大速度方向与轴向呈约45°，经过多级刷丝束后下游区速度增大，且靠近转子面位置气流不稳定。两级低滞后型刷式密封最大速度略大于三级低滞后型刷式密封最大速度，两者相差不大。

图11 两级低滞后型刷式密封速度矢量图Fig.11 Two-stage low-hysteresis brush seal speed vector

图12 三级低滞后型刷式密封速度矢量图Fig.12 Three-stage low-hysteresis brush seal speed vector

3.3 温度分布特性分析

图13和图14分别给出了在压比为3，干涉量0.3mm条件下两级和三级低滞后型刷式密封的温度分布云图。由云图可知，两种刷式密封结构上游区域温度均较低，经过第一级刷丝束温度升高，在刷丝自由端温度较高，刷丝固定端温度较低，第二级刷丝温度明显高于第一级刷丝，且温度径向传递较强，三级刷式密封第三级温度明显高于前两级，径向温度传递最强，此时刷丝根部温度也较高。三级刷式密封最高温度高于两级刷式密封最高温度，这主要因为三级刷式密封刷丝级数多，从而摩擦产生热量较多，且密封性能较好，不利于散热，从而导致三级刷式密封最高温度大于两级刷式密封最高温度。两种形式刷式密封的最高温度位置均出现在末级刷丝自由端位置，主要是因为刷丝与转子之间摩擦会产生大量的热，而泄漏气流与前一级刷丝之间对流换热，泄漏气流流经后一级刷丝再次与后一级刷丝进行对流换热，最终导致末级温度最高。两种刷式密封结构，下游区温度均明显升高，且靠近转子面位置温度较高，主要是因为泄漏气流将上游刷丝区域的温度带至下游区。

图13 两级低滞后型刷式密封温度分布Fig.13 Temperature distribution of two-stage low hysteresis brush seal

图15和图16分别给出了在压比为3，干涉量0.3mm条件下，两级和三级刷式密封刷丝自由端位置的轴向温度分布。图中第1根至第19根刷丝表示不同级刷丝束从前挡板至后挡板位置刷丝，可以看出，两种结构刷式密封第一级和第二级刷丝自由端温度沿轴向逐渐升高，且第二级刷丝温度明显大于第一级刷丝温度，随着靠近后挡板位置，第二级刷丝温度与第一级刷丝温度差明显增大，三级刷式密封第三级刷丝温度最高。两种刷式密封结构的刷丝最高温度均发生在末级刷丝束末排位置，这主要是气流将前排刷丝温度带至后排刷丝，从而导致末排刷丝温度较高。

图15 两级低滞后型刷式密封刷丝自由端轴向温度分布Fig.15 Axial temperature distribution of brush wire free end for two-stage low hysteresis brush seal

图16 三级低滞后型刷式密封刷丝自由端轴向温度分布Fig.16 Axial temperature distribution of brush wire free end for three-stage low hysteresis brush seal

3.4 刷式密封刷丝热变形分析

本文利用CFX计算得到多级刷式密封温度分布，并在Workbench建立热力学模块，利用流固耦合方法将流体域计算得到的温度通过对流换热耦合面进一步传递至刷丝，进而来分析刷丝的热变形情况。

图17和图18分别给出了在压比为3，干涉量0.3mm条件下，两级和三级刷式密封温度对刷丝变形的影响。由图可以看出，两种形式刷式密封结构刷丝的变形量逐级增大，且最大变形位置出现在末排刷丝自由端位置，这主要是因为末排刷丝温度较高，因此热变形也较大。两种刷式密封形式的每级刷丝束固定端位置基本不发生热变形，这是由于刷丝固定端温度较低，在相同条件下，三级刷式密封的热变形量要大于两级刷式密封的热变形量，这主要是因为三级刷式密封刷丝级数多，刷丝与转子之间摩擦产生的热量较多，且不利于热量的散失，这就造成了三级刷式密封刷丝热变形较大，在压比为3条件下，三级刷式密封刷丝热变形约为两级刷式密封刷丝热变形的2.6倍。