一种联轴器动力学简化计算方法与验证*

（沈阳鼓风机集团股份有限公司）

0 引言

振动水平是衡量压缩机产品质量的一个重要指标。压缩机的厂内试车过程是检验压缩机性能和质量的重要环节，同时也是产品交予用户前的一道关键的安全保障。当振动问题发生时，用户及现场人员更加关注的是产品本身是否存在问题。联轴器作为机组驱动机与被驱动机的连接/保护部件，一方面承担扭矩传递的功能，一方面为转子安全运行提供保护作用[1-8]。如果联轴器固有频率与机组本身的转动频率接近，就会引起机组的振动停车。国内对于联轴器的研究主要局限于具体产品的设计改进，多采用有限元法进行分析[9-12]，近年来对压缩机用联轴器动力学分析的理论研究也比较少见。

本文以一款联轴器为案例入手，开展其动力学分析。通过参考梁的固有频率理论计算方法[13-14]进行研究和计算，随后针对实体简化模型进行了有限元分析和相互比对验证，最终给出联轴器的固有频率简化计算方法以及适用范围，以便于后续的工程应用。

1 理论计算

以一款联轴器（型号HS8370）案例入手，其结构细节如图1所示，联轴器厂家提供的一阶固有频率为7 909rpm，长度2.374m，外径φ0.24m，中段的长度与外径比值为8.3（以下简称中段长径比），中段长度为总长的83.8%，中段质量为总质量的64.9%。由图1可知联轴器主要由三个部分组成：驱动侧（52kg）、中间段（192kg）、被驱动侧（52kg）。其截面刚度也如此区分。则可将其力学模型简化为如图2的结构形式。

图1 联轴器结构简图Fig.1 Structural diagram of the coupling

图2 联轴器理论计算简化模型Fig.2 Simplified model of the coupling

根据简化后的理论计算模型应用结构动力学理论公式进行求解计算。其计算方法如下：

假定其驱动侧、中间段、非驱动侧的质量分别为M1，M2，M3，在三个质量等效位置处加载后的竖向变形分别为Y1，Y2，Y3，则根据柔度系数δij与变形关系可以获得如下关系式：

其中（i=1，2，3）

其柔度系数δij可写成矩阵形式：

假定变形Yi的通解为：

代入关系式（1），可以得到如下结果：

整理后可得关于Ai的三元一次方程组：

Ai有非零解，所以其方程组的系数行列式应等于零：

对于联轴器的简化模型而言，质量Mi是已知的，为求解系统固有频率，则需要首先求解柔度系数δij，其求解方法可根据梁的挠度公式进行求解，单位力分别作用于不同的质量点位置，分别计算在单位力作用下的不同质量点位置的挠度（连接处变截面刚度需要考虑在内）。

联轴器的固有频率理论计算过程中，突出需要解决的有两个问题，一个为挠度矩阵的计算，一个为一元三次方程组的解法。

考虑变截面梁的挠度叠加问题，以图3模型为例，其挠度产生主要为集中力产生的挠度和弯矩产生的转角，挠度采用悬臂梁公式的叠加方式，其中心处的挠度公式为：

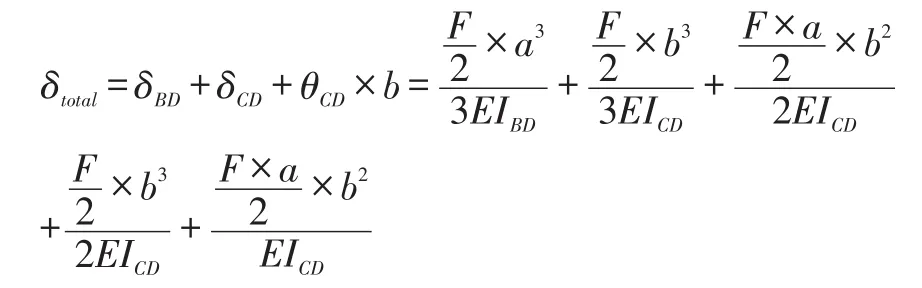
图3 梁挠度理论计算简化模型Fig.3 Simplified model for the deflection's calculation

由此叠加法可以计算出挠度矩阵的各项值。而根据矩阵运算后会生成一个一元三次方程组，其解为结构的固有频率。而一元三次方程组的解法可根据卡丹公式获得，其公式如下：

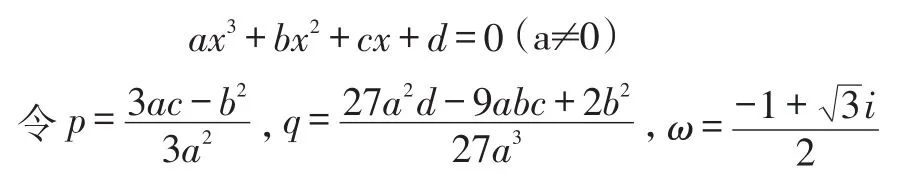
有：

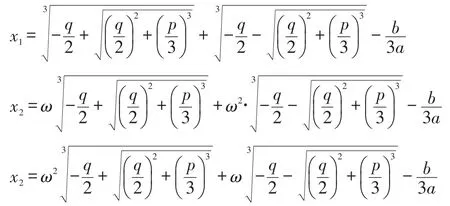
经计算本文中联轴器的挠度系数矩阵结果如下：

将已知的Mi，δij代入关于Ai方程组的系数行列式，并假定，就可获得关于X的一元三次方程组：

求得：

即求得固有角频率ω：

计算获得联轴器的一阶弯曲固有频率为119.4Hz（7 162r/min）。

为考察理论计算的适用性，对该联轴器开展有限元分析，进行固有频率结果的比对工作。

2 有限元分析

首先根据联轴器的结构特点进行三维有限元建模与简化，其简化的结构模型如图4所示。将简化后的三维实体模型导入有限元分析软件ANSYS进行有限元模型的建立，以10节点4面体单元SOLID187为主，建立单元数为63 140、节点数117 918的有限元模型，如图5所示。

图4 三维分析用联轴器模型Fig.4 Coupling model for 3D analysis

图5 三维分析用有限元模型Fig.5 Finite element model for 3D analysis

针对联轴器两侧的连接端面采用简支的位移约束形式，采用BLOCK LANCZOS法对联轴器有限元模型进行模态分析，获得联轴器的一阶弯曲固有频率为143.1Hz（8 586rpm）。其振型图如图6所示。

图6 联轴器一阶弯曲振型图Fig.6 First order bending mode shape of coupling

根据联轴器图纸所标定的实测固有频率，将联轴器的理论计算和有限元分析获得了联轴器的一阶弯曲固有频率进行比对，计算结果比对如表1所示，由表1的对比可知，因模型简化导致的有限元分析误差也达到了8.6%，而理论计算的偏差为9.4%。一般在工程应用中，动力学干涉评判的裕度选取10%到20%[15]，故此理论方法所计算得到的一阶固有频率，精度基本满足工程需求。

为确定公式法的适用范围，进一步的开展了多款联轴器的应用与结果的验证。

表1 联轴器计算结果比对Tab.1 Comparison of coupling calculation

3 公式法验证

公式法在实际运用的过程中，需要输入的参量主要包括：联轴器简化的三段质量、质心位置、三段截面内外径数据。

随机选取额外11款联轴器进行公式验证和整理，其数据如表2所示。可以看出固有频率的计算误差与输入参数的大体规律。

从表2数据以及图7也可以看出，针对中段的长径比大于3，中段的长度比总长大60%，且中段的质量比总质量大50%的联轴器，理论计算能够得到较低的偏差。满足上述条件的联轴器，理论计算结果偏差基本能控制在15%以内。基本可满足固有频率快速计算和现场问题排查的精度要求。

表2 联轴器一阶弯曲固有频率计算结果Tab.2 Calculation results and error of coupling's first-order bending frequency

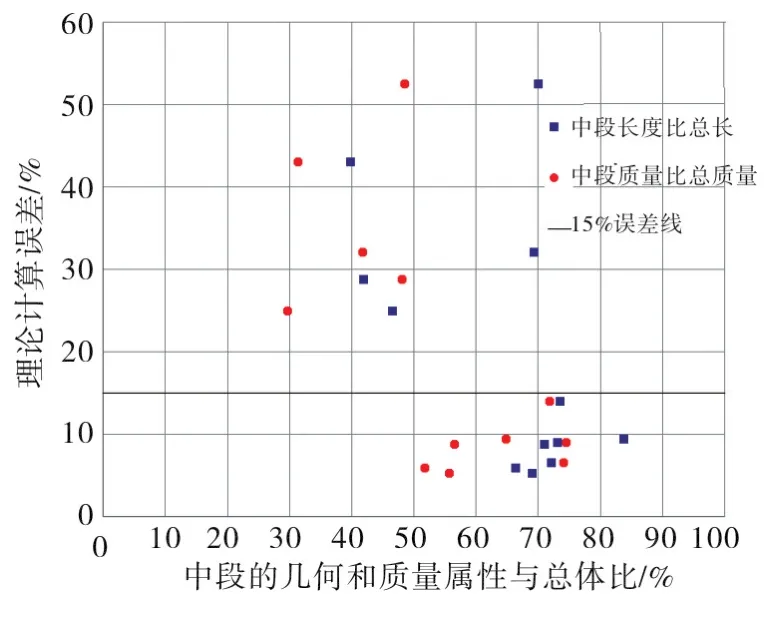
图7 联轴器理论计算误差分布图Fig.7 Calculation error distribution of coupling

针对联轴器的一阶弯曲固有频率的理论计算，在AGMA 9104[15-16]中有相关的描述，其计算方法的简化前提是等截面圆管，刚性支撑条件下的频率计算。针对本文提及的12款联轴器数据进行代入公式计算可以得到如表3的结果和对比。

表3 AGMA公式法计算结果Tab.3 Calculation results of AGMA formula method

其中，误差定义为：

式中，F代表理论计算频率；f代表实测频率。产生误差的根本原因在于理论计算过程中的质量和刚性的简化等效。本文的方法进一步的考虑联轴器两端的变截面属性以及实际的质量属性，相比AGMA法的主要区别在于从单一质量和刚度等效变为分三个区域进行刚度和质量等效，故理论计算的误差有所降低。

从表3可以看出，文中所提及的限定范围内的联轴器，本文的方法能够更好的预估联轴器频率，而范围外的大部分联轴器，文中方法与AGMA标准的计算结果相近。

4 结论

由以上计算过程和计算结果可得出以下结论：

1）通过理论计算得到的案例联轴器的一阶弯曲固有频率偏差为9.4%；

2）针对中段的长径比大于3，中段的长度比总长大60%，且中段的质量比总质量大50%的联轴器，此理论计算方法能够得到满足工程应用的精度需求；

3）提取联轴器的关键几何和质量属性数据，应用此套理论方法，能够快速得到限定条件下的联轴器一阶固有频率。