在问题解决中探寻学生的思维路径

◇程翠萍 王玉玲 赵瑞杰

一、问题的提出

为了探寻学生在解决问题中的思维路径，我们结合北师大版小学数学五年级教材精心编制了5 道“有充分思考价值、适宜探究空间、无限对话可能”的测试题。测试中，让学生在自主、自然的状态下完成，教师观察学生能动的、自觉的、习惯化的思维情况，以挖掘学生内心深处的数学思考。

二、调研的内容、结果、分析

在调研中，我们主要采用问卷调查、个别访谈的方法，对鹤壁市3 所小学共150 名五年级学生进行了调研。

第1 题用长度为1 米的三根小棒围成一个等边三角形，这个三角形的面积是（ ）。（选择合适的选项）

A.1 平方米

B.比1 平方米小而比0.5 平方米大

C.0.5 平方米

D.比0.5 平方米小

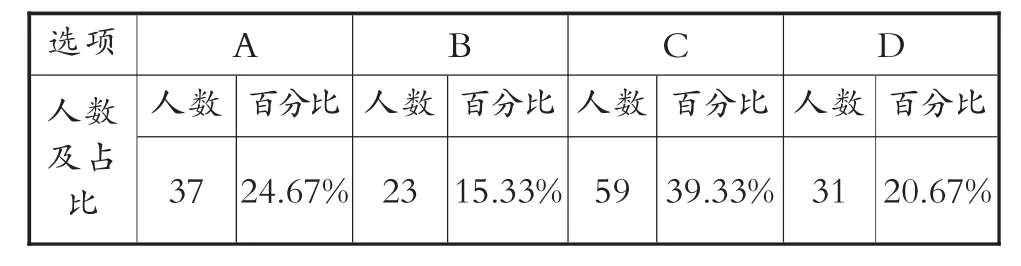
A B C D人数 百分比 人数 百分比 人数 百分比 人数 百分比37 24.67% 23 15.33% 59 39.33% 31 20.67%选项人数及占比

面对等边三角形面积的计算，有的学生忽略了寻找对应的底和高，第一反应是用相邻两边相乘得到1，于是选择A；有的学生又想起三角形面积公式中的除以2，于是选择C；有的学生发现这个三角形的面积比边长为1 米的正方形面积要小，没有辨别三角形面积与0.5 平方米的关系，于是选择B；有的学生明白三角形面积公式，发现三角形的底是1 米，而高不知道是多少，但发现高一定会小于斜边1 米，于是选择D。

观察并分析学生思考问题的路径，不难发现不少学生对三角形面积公式的理解还存在模糊的认识，运用知识解决问题缺乏相应的方法和策略（画图、推理、比较）。学生习惯于问题解决的最后是具体的算式、准确的答案，因而选择答案A、C 的学生之和占总人数的64%。

虽然该题中等边三角形的面积是一个能计算出的具体数，但由于小学生学识、能力达不到，本题的初衷是让学生通过数学推理确定等边三角形面积的大小范围即可，但小学生对此不适应，约15%的学生能够想到或画出“底边上对应的高”，只是因它的具体值无法确定所以没有更深入地去研究它的范围。 仅有约21%的学生通过画图、推理判断出等边三角形面积大小的范围。

由此可知，学生的思维路径符合小学生的思维发展规律，即由具体思维逐步向抽象思维过渡。其过程是缓慢的、渐变的，需要教师润物细无声的浸润和滴灌。

第2 题计算×2×3×4×5。

选项人数及占比结果为154 结果为4 结果是其他人数 百分比 人数 百分比 人数 百分比54 36% 57 38% 39 26%

图1

在结果正确的人群中，约28%的学生绕过了乘法分配律，“中规中矩”地（如图2）得出答案。

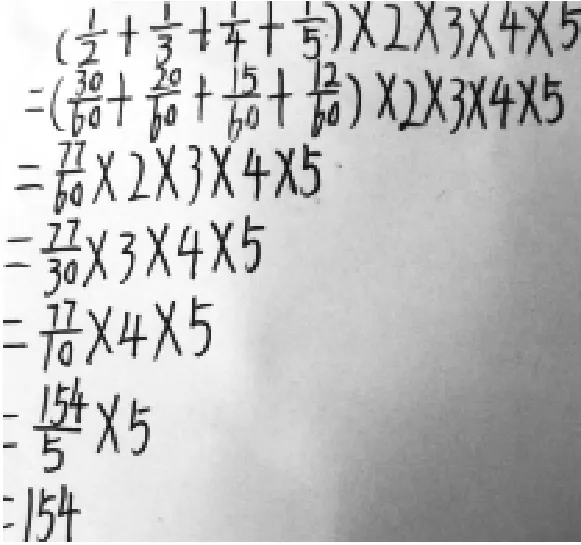
图2

约8%的学生（如图3）显示出已对乘法分配律有深刻的理解，且能正确地运用，透过现象看到了本质，能把2×3×4×5 看作一个数，这是一种整体思想，对于学生来说算是一种创造了。

图3

第3 题数m、n、t 在直线上的位置如图4 所示：与数t 最接近的是（ ）。 （选择合适的选项）

A.m＋n B.n－m C.n×m D.n÷m

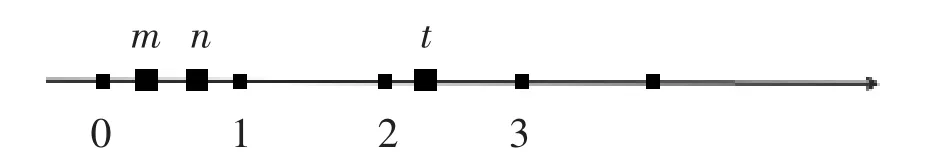
图4

人数及占比人数 百分比 人数 百分比 人数 百分比 人数 百分比44 29.33% 3 2% 40 26.67% 63 42%

此题巧妙地将小数加、减、乘、除运算同数轴相结合，考查学生对“大于0 且小于1 的小数加、减、乘、除运算结果”的数学经验是否准确、恰当。在选择D 的学生中能够清晰表达的学生仅占16%（如图5），剩下的26%是借助数形结合假设具体数计算（如图6）或直观发现m 和n 的关系（如图7）巧妙解决问题，策略的灵活运用让问题解决化繁为简，化难为易。

图5

图6

图7

整数、小数、分数的除法计算分散到不同的年级中进行学习，在实际教学中，教师往往会忽略它们之间的联系，学生很难整体建构知识体系，不少学生对小数除法算式结果的认知仍停留在整数除法认知水平，总认为经过除法计算的结果会更小（如图8）。

图8

第4 题72AA3A 是一个六位数，它一定是（ ）的倍数。（选择合适的选项）

A.2 B.3 C.5 D.不能确定

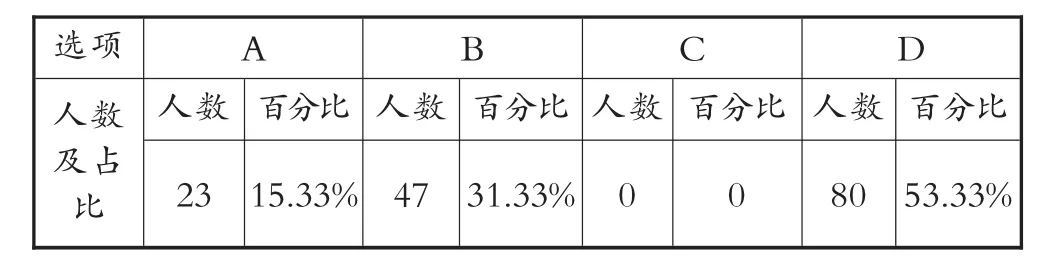
A B C D人数 百分比 人数 百分比 人数 百分比 人数 百分比23 15.33% 47 31.33% 0 0 80 53.33%选项人数及占比

此题考查的显性知识是2、5 和3 的倍数的特征，隐性知识是探寻3 的倍数特征背后的原理。不少学生想不到去抽象这个六位数的数字之和，约69%的学生选择了A 和D，他们对2、5和3 的倍数的特征以及判断方法已经熟练掌握（如图9），但不能有效地对问题进行分析、归纳、总结、提升而“半途夭折”，很显然是缺乏解决问题的策略和方法。

图9

选择B 的学生中有16%是假设A 为0～9 中的一个（如图10）进行判断，这种方法属于不完全归纳，不完全归纳得到的结论准确可靠吗？怎样启发学生确认不完全归纳法获取结论的正确性？从学生的分析解答中映射出“小学教师在归纳推理的认识、理论、方法、技能等方面存在严重缺失”。

图10

只有约15%的学生把“3A+12”作为结果来判断它是否为3 的倍数，并通过数学分析获取结论（如图11），属于演绎推理。研究表明：演绎推理能力随着年龄的增长而提高，它在小学阶段就得到了发展，不同的教学水平对演绎推理正确性的影响具有显著差异性。

图11

第5 题一个正方体的展开图如图12 所示，把它折叠成正方体时，点A 和点（ ）重合。

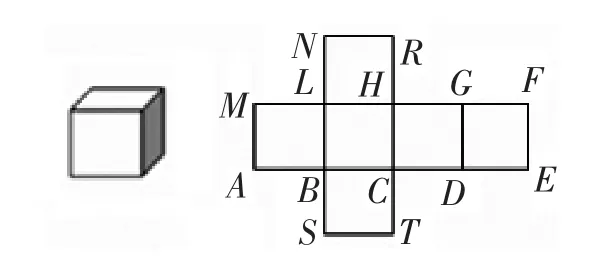
图12

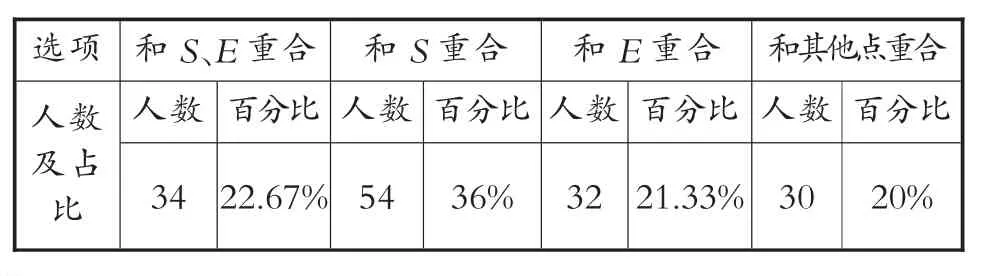
和S、E 重合 和S 重合 和E 重合 和其他点重合人数 百分比 人数 百分比 人数 百分比 人数 百分比34 22.67% 54 36% 32 21.33% 30 20%选项人数及占比

此题考查平面图形和立体图形相互转化中关键“元素”之间的对应，要求学生具有较强的空间想象能力。36%的学生发现点A 和点S 重合，思考的路径是把正方形BCHL 作为正方体的底面，正方形ABLM 和正方形BCTS 分别作为正方体的左面和前面，在这次想象中点A 和点S 正好重合。为了表达得清晰、简洁，有些学生用不同符号来表示各个不同的面 （如图13），显示出较强的符号意识，有一定的解决问题的策略。

图13

约21%的学生发现点A 和点E 重合，思考的路径是把正方形ABLM 作为正方体的左面，正方形CDGH 就是正方体的右面，那么正方形DEFG 是正方体的上底面，在这次想象中点A 和点E 正好重合。 约23%的学生能够把这两次想象合二为一（如图14），发现点A、点E 和点S 重合。

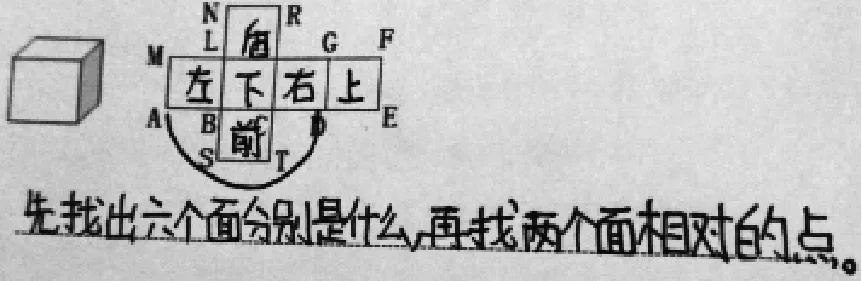
图14

三、对教学的启示

1.从思维路径中的“拐点”发现学生对概念的认识不准确，对规律的本质把握不到位。

正确的背后可能隐藏着模糊，甚至错误的认知。学生掌握了知识还是会犯错，这些错误往往是思维方式的不同导致的。学生的思维容易倾向解决问题时的“舒服”“方便”“简洁”，简单的类比和受思维定式、顺向思维的影响造成偏离数学的本质的现象。

当学生基本概念不清的时候，面对稍微具有灵活性的变式题目，往往会出现思维混淆的现象。如第1 题中，学生是能够正确地表述三角形面积计算公式的，但在实际运用中往往不去判断底和高是否对应或者忘记除以2。第2 题中×2×3×4×5”和考查的同样是分数乘法分配律，所不同的是后者为标准格式，前者为变式，将括号外的一个数转换为一组数连乘的形式。

知识贵在求联，联则通，通则透。当学生把知识间的联系与变通潜在地沉淀下来，自觉地实现观念的更新和知识的重构时，其数学素养才会悄悄地得到发展。

2.从思维路径中的“错误点”发现学生对数学经验提升的缺失，映射出探究过程中的体验、感悟不足，造成学生数学认知结构的不完善。

审视第3 题的“思维路径”，发现学生对小数除法的认知没有同整数除法相互关联和对比，而小数除法的学习是介于整数除法、分数除法之间，作为 “桥梁” 要沟通它们三者的联系。 将来学习分数除法运算时同样要和整数、小数的除法运算相关联，最终让学生建立“除法计算” 完整的知识结构和体系，理解三者相同的本质。

3.从“不同”的思维路径中发现学生问题解决的策略缺乏科学性。

第3 题思考的路径是从一般中寻找特殊，m、n 取符合题意（0＜m＜n＜1）的所有数均能获取正确的答案。第4 题思考的路径是从特殊中寻找一般，六位数72AA3A 中A 可取0、1、2……9 共10 种情况，研究完所有情况下的结论则是科学的。如果不能研究完所有情况就需要进行整体分析、分类讨论……小学数学教学中渗透特殊化与一般化方法对学生进一步学习数学和解决问题将有积极意义。 第5 题思考的路径需要把正方体表面展开图在头脑中完成折叠操作，较高的错误率反映出空间观念的欠缺。

通过研究学生在问题解决中的思维路径，可以真实地再现学生隐形、个性的思维，读懂学生学习起点、难点、差异及需求。教学中，我们要顺应学生思维路径，在认知的狭隘、粗浅、偏颇、混沌、疑惑、困难处设置“障碍”引发矛盾冲突，追溯思维原点，挖掘、拓宽思维的难度和深度，引领学生思维向纵深发展，向学科本质发展。