以臆测教学促进学生对分数意义的理解
——以“分数作为整数相除的结果”教学为例
2019-11-14蔡宝桂
◇蔡宝桂

一 “作为整数相除的结果”的分数意义
有关分数意义的研究,不论中外学者如何区分建构意义的种类,都少不了“商”的意义,即对应于小学数学教材中分数意义之分类“作为整数相除的结果”。
首先,平均分情境是“总量÷单位数=单位量”,如“3 个比萨平均分给4 个人,每人得到个比萨”,从问题记录而言,除法算式表征为“3÷4=3 4 ”;反之以乘法算式表征则为“()×4=3”,也就是“平均每个人分得个比萨,4 个人一共可分得3 个比萨”。因此其分数意义体现在“单位分量”上,对数概念的认知则发展为部分-整体关系,如图1。

图1:平均分情境下3÷4 的图形表征
其次,测量情境即为包含除,也就是“总量÷单位量=单位数”,如长7 厘米的缎带,每4 厘米剪一段,可以剪一段剩下3 厘米,以段为单位这3 厘米又可以称为段,所以算式可以写成7÷4=1,意义沟通为7 是4 的1倍,也可以换成假分数,而理解此学习活动须具备 “分数倍”的概念,认知发展涉及“比例思维”,如图2。
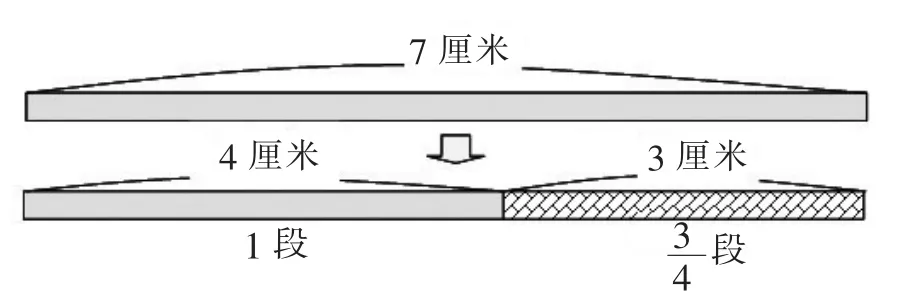
图2:测量情境下7÷4 的图形表征
二 学生学习所需具备的知识基础
因此,四年级学生学习整数相除的结果为分数的意义前,须具备将分物视为“单位分量”的分数意义,也就是要从原本的“分几份取几份”的“部分-整体”的分数意义,对照整体量“1”这一单位,将每个单位分数都视为一个独立可计数的量,建立单位分量的分数概念,如图3。

图3:从“部分-整体”扩展到“单位分量”
因此,教师教学时建议给定明确的大小单位,如大单位“1 张”、小单位“1 片”,让学生在对应原有“部分-整体”的图示表征(如图4)中,最终发现小单位摆放的位置并不影响小单位的大小,进而认识到即使脱离1 张,仍然是可被独立计数的单位分量。此时,学生对于分数的认识才由“分几份取几份”的描述词,进展到对计数单位的认识,也才能以此作为分数数词序列计数的基础。

图4:形成单位分量之“片”于“张”的操作流程图
三 数学臆测教学案例摘要
以下分别从林碧珍(2018)的数学臆测教学模式中所提出的五阶段分别进行说明。(“分数作为两数相除的结果”的内容安排在四年级)
(一)造例。
1.造例设计。
(1)利用学生不等分组的组内人数(b)与限时分割彩纸张数(a),达到全班造出多种分母(b)和分子(a)的分数。
2.造例活动。
为达到上述造例设计要求,班级学生的座位应以不等组的方式安排,再加上考虑限定时间内,让每组得以操作体验“一回拿一张,一张分给几个人”的数学结构,所以每组须安排小帮手,负责提供彩纸,且同组的每张彩纸颜色都不同。组内任务进行步骤说明如下:(如图5)
步骤一:小帮手将一张圆形彩纸交给组内其中一人。
步骤二:先对折再剪开,并将每小片分给组内除小帮手外的每一个人。
步骤三:拿到纸片的同学,需在每小片彩纸上写出几分之几张。
步骤四:一张圆形彩纸平分完后,小帮手再发一张新的圆形彩纸给组内另一个人。

图5:造例活动座位安排与角色分工示意图
游戏结束后,可请学生数自己分得的彩纸,并让其他组的学生从分得彩纸的结果,猜猜看:这组有几个人在分彩纸?这组刚刚分下去几张彩纸?作为引发学生进行后续一连串深入探究的动机。
3.造例汇总。
(1)请学生用算式记录每一组分得彩纸的过程与结果,学生可能以乘法算式表示分得的结果,除法算式表示分的历程或摘要记录,如图6。

图6:算式记录分得彩纸的过程或结果
(2)讨论完每一组的算式记录是过程还是结果后,教师再请学生“用一个算式把分彩纸的过程和结果记录下来”,将学生对于造例活动的算式表征,推进到以一个除法算式摘要记录的程度。
(3)由教师汇总全班造例于黑板上,让学生依此提出后续的数学猜想。
(二)提出猜想。
教师进行个别观察,并全班汇总后,发现的数学想法可分为以下几类,举例如下。
1.现象描述。(如图7)

图7
2.结果都是分数。(如图8)

图8
3.算式中的数字关系。(如图9)

图9
4.被除数与分子相同。(如图10)

图10
5.除数与分母相同。(如图11)

图11
6.被除数与分子、除数与分母。(如图12)

图12
7.数字大小的比较。(如图13)

图13
8.单位分量描述。(如图14)

图14
9.关系的推论。(如图15)

图15
(三)效化猜想。
1.猜想语言描述的精确性。
(1)学生只描述上、下,经讨论后认为应该用分母和分子的语言来描述才能更精确地表示。(如图16)

图16
(2)答案还是“分数”?
“答案是偶数”,有违学生在整数前提下进行奇偶分类。因此,须修正为“答案中的分母都是偶数”。 (如图17)

图17
“答案有两个数”,是指有两个答案?可能是因为答案用分数表示,所以分数线上下各有一个数,所以有“两个数”。(如图18)

图18
2.修改或删除错误猜想。
(1)“有几个吐司”应该修正为“有几个人来分吐司”,才能使猜想由错误变正确。(如图19)

图19
(2)“除法的余数加回去”,虽然知道学生想表达的是不写整数商和余数,而是直接写用分数商表示,但讨论的当下,学生觉得“加回去”这个词有错,但又不知如何修正,所以这个猜想就被删除了。(如图20)

图20
3.避免使用否定词或限制性词语,如在数大小比较中有关 “有一些算式的结果,分母比较大、分子比较小”,虽然可找到分母大于分子的例子,但因为这句话用了“有一些”后,无法因错误而被推翻。所以,一开始就要反复提醒学生,这类词不要出现在猜想中。
4.提出反例从而删除猜想。
(1)如果讨论的时间够长,可不可能分超过10 张以上?一组人数多一点,超过10 人以上,如20÷23=就可以推翻类似以下这样的猜想:数大小比较的猜想“每个数都不比10 大”、现象描述的“算式中没有0”、“答案中的分母都是偶数”的猜想。
(2)每个“算式都没有0”是数字中有无0 之外,还包含0 可否当被除数或除数,因此也可以以0÷3 举反例,但对于学生而言,没有东西却要分给人,也是比较难以接受的,虽然它符合数学定义。
5.汇总猜想:在讨论进行猜想的分类、检验与效化后,猜想大约被汇总为三大类:其中单位分量描述与关系的推论仍各为独立的一类,前面7 项都被归为一大类,并成为猜想一般化的讨论题材。
(四)猜想一般化。
经过学生对猜想进行检验、支持或应用扩充例子反驳的历程后,最后提出一般化的猜想:所有整数除以整数(不包含0),当答案用真分数或假分数表示时,被除数会变成分子,除数会变成分母。
(五)证明猜想一般化。
有关单位分量与关系推论的猜想,是学生成功证明此一般化猜想的重要题材,再加上一开始造例活动所提供的操作体验,学生提出以下论证的观点来说服他人,这个一般化猜想一定是对的,也提升了对被除数、除数和商的分子与分母之间意义的理解。进而发现,虽然之前认为被除数和分子、除数和分母都是相同的数,但这个一般化猜想中的“变”字,就点出了两者之间意义的新解。
如被除数的“分几张”,到了商的分子却代表“分得几个单位分量”,而除数的“分给几人”,到了商的分母却代表“被计数的单位分量”。(如图21)

图21
荷兰学者斯特瑞夫兰德(Streefland,1991)认为,极度低估学生学习分数时的复杂性与机械化取向的分数教育是分数教学与学习问题的两个源头。杰罗姆·布鲁纳(Jerome Seymour Bruner,1966)也曾说过:“任何学科均能以某种智慧上真实的形式,有效地教给任何发展阶段中的任何一个儿童。”只要对应学生数学概念发展,用对分数意义的诠释,加上学习者体验、表征,进而迈入数学论证的学习模式,分数将不再是阻碍孩子数学学习的梦魇。
