一种改进的K-Means算法

韩存鸽，刘长勇

(1.武夷学院数学与计算机学院，福建 武夷山 354300；2.认知计算与智能信息处理福建省高校重点实验室，福建 武夷山 354300)

数据挖掘是一个年轻而充满生机的领域，常用的数据挖掘技术有决策树、聚类挖掘、神经网络、规则归纳、遗传算法、统计学习、联机分析处理等，其中聚类挖掘在数据挖掘研究领域中扮演着非常重要的角色，是一种无监督的机器学习算法。K-Means 算法是J.B.MacQueen在1967年提出的一种聚类挖掘算法，同时也是一种经典的基于划分的聚类分析方法，该算法将一个给定的样本数据集划分为由若干相似实例组成的簇的过程，聚类结果使得同一个簇内的相似度高，而不同簇之间的相似度最小化[1]。

虽然K-Means算法已经得到广泛的应用，但该算法本身也有一些不足，从而吸引了许多研究人员对其进行改进，相继衍生出了许多改进的K-Means 算法。文献[2]提出一种用多层受限玻尔兹曼机(RBM)对数据进行特征学习，采用深度信念网络(DBN)对相关参数和初始聚类中心进行交叉迭代优化算法。文献[3]提出一种关系矩阵和度中心性相结合的分析方法的来确定K-Means算法中的k个中心点。文献[4]提出一种基于K-Means分层迭代的检测算法，通过多次属性消减的K-Means聚类迭代操作来检测到不同异常类型的攻击。文献[5]提出了一种改进的自适应双层变量加权K-Means算法，该算法根据数据集的特点自动聚成合适的K个簇。本文提出一种基于最大最小距离和BWP指标相结合的K-Means算法，为了验证改进算法的性能，本次实验对UCI数据库中的4个数据集进行仿真测试，根据实验结果，改进后的算法在准确率、聚类效果两方面有一定的优势。

1 K-Means算法理论

K-Means算法对数据进行聚类的过程为：首先将数据集随机的分为k类，分成的这k个类中包含若干对象，计算每个类簇的中心。接着对剩余的每个对象，根据簇均值的距离按照就近原则分派给最近的簇；最后继续计算每个簇的新均值。直到准则函数收敛，否则该过程将会一直重复执行，通常，采用平方误差准则，其定义如下[6]：

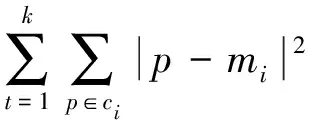
(1)

其中，p表示数据对象；mi是簇ci的平均值。

K-Means算法的流程如下：

输入：聚类数目k和数据集D={d1,d2,…,dn}

输出：k个类簇，满足平方误差准则函数收敛

1)从数据集D中任意选择k个数据对象作为初始簇中心；

2)repeat；

3)根据簇中对象的均值，将每个对象赋给最相似的簇；

4)更新簇均值，即计算每个簇中对象的平均值；

5)计算聚类准则函数；

6)直到准则函数值不再进行变化，算法结束。

K-Means算法缺点[7]：

1)需要预先指定聚类数目k值，而现实生活中，用户在对数据集进行聚类的时候刚开始并不知道应该分几类合适，也就是说这个聚类数目k值不好估计。

2)质心不确定，需要对质心多次循环才能达到收敛，从而使K-Means算法陷入局部最小解，无法做到全局最优解。

3) 初始簇中心不同使得的聚类结果可能不同。

2 改进算法的理论依据及改进后的算法

针对K-Means算法需要预先指定类簇的值、质心选择不确定、初始簇中心的选择敏感等不足，本文提出一种基于最大最小距离结合BWP指标的UPK-Means聚类算法。

2.1 最大最小距离算法思想

最大最小距离算法核心为：取尽可能远的对象作为聚类中心,是一种以欧氏距离为基础的聚类算法。该算法最直观的优势是可以避免K-Means算法的聚类种子过于临近问题，它不但能够智能地确定初始聚类种子的个数，而且还能提高划分初始数据集的效率。

最大最小距离算法的主要流程[8]如下：

1)从数据集X={X1,X2,X3,…,Xn}中任取一个样本作为第1个聚类中心，如取C1=X1;

2)计算其他所有样本到C1的距离Di1，若Dk1=max{Di1}，则取C2=xk;Di1=‖xi-C1‖=

3)分别计算D中剩余的样本到C2的距离Di2，假设Di=max{min(Di1,Di2)}，i=1,2,3,…,n,若Di>θ·D12(C1到C2距离)，则取xi为第3个聚类中心，记作C3=xi;

4)如果C3存在则计算Dj=max{min(Di1，Di2，Di3)}，j=1,2,3,…,n,若Dj>θ·D12(C1到C2距离) 则取xj为第4个聚类中心，记作C4=xj以此类推，直到最大最小距离不大于D12时，寻找聚类中心的计算结束；

5)对所有样本按照就近原则划分给距离最近的聚类中心，然后根据某聚类准则考查聚类结果，若不满意，则重新选择C1与θ，重新进行相关距离计算，直到满意算法结束。

2.2 最大最小距离算法应用举例

假设有7个模式样本点{X1,X2,X3,X4,X5,X6,X7}，对样本进行聚类分析，7个二维样本为：X1=(0,0)，X2=(1,3)，X3=(2,2)，X4=(6,7)，X5=(0,1)，X6=(5,6)，X7=(8,1)

1)任取一个样本点作为第一个聚类中心,这里取C1=X1=(0,0)，分别计算所有样本到C1的距离,为了更直观地显示计算过程，计算结果如表1所示。

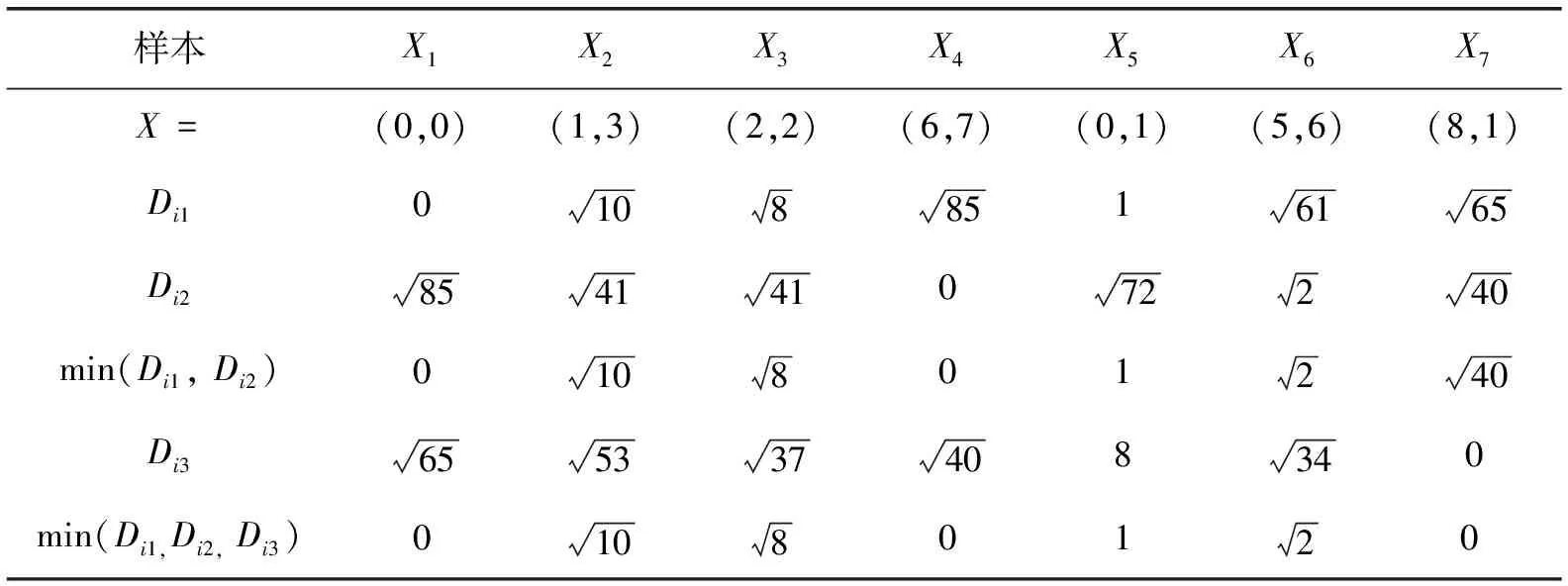
表1 样本到C1的距离

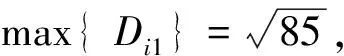
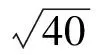
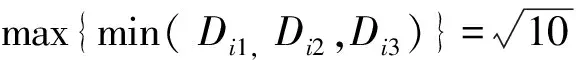
4)根据计算结果，本例只有C1、C2、C3这3个聚类中心，分别为按照最近原则把所有样本划分给距离最近的聚类中心。{X1,X2,X3,X5}∈C1，{X4,X6}∈C2，{X7}∈C3，该聚类结果与传统的K-Means算法的聚类结果完全一致，传统K-Means算法的聚类过程这里不做赘述。

2.3 BWP 指标函数

目前经常被人们使用的检验聚类有效性的指标有XB指标 (Xie-Beni) 、KL指标 (Krzanowski-Lai) 、Sil指标 (Silhouette) 、DB指标 (Davies-Bouldin)、IGP指标 (In-Group Proportion)、BWP指标 (Between-Within Proportion) 等。其中BWP 是一种有效的聚类指标，该指标依据簇内相似与簇间相异两方面来评判聚类结果。如果X={X1,X2,…,Xn}为聚类数据集，k= (X,R) 为聚类空间, 如果数据集中的n个样本分为c类，则最小类间距离、类内距离，BWP指标判别函数公式如下[9]。

最小类间距离：

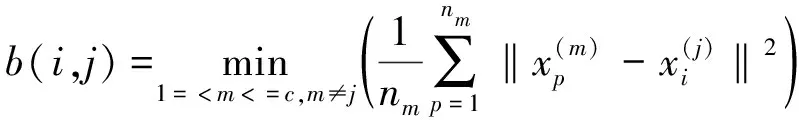
(2)

类内距离：

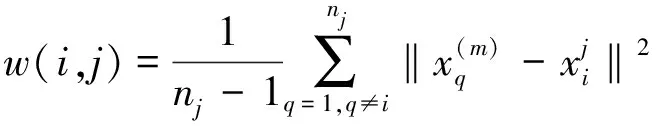
(3)

BWP指标：

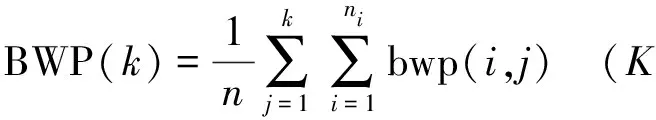
(4)

其中BWP指标值越高，聚类性能越好,BWP指标确定k值。

对于单个样本来说，若BWP指标值越高，则意味着聚类性能就越好。那么对所有样本来说，要取BWP的平均值来观察聚类性能，BWP平均值越高，数据集的聚类性能就会越好[10]。其中avgBWP(k)为所有样本的BWP平均值，kopt为聚类数，计算公式如下：

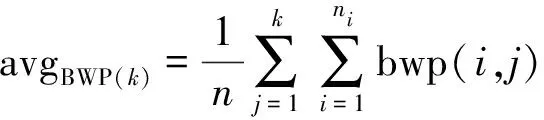
(5)

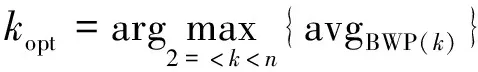
(6)

2.4 基于最大最小距离和BWP指标优化的K-Means算法改进

本文提出一种基于最大最小距离和BWP指标相结合的K-Means算法，以下命名为UPK-Means，改进后算法的基本思想如下:假如数据集X={X1,X2,X3,…,Xn}可分为K类，K数目未知。首先在X中找出距离最远的两个样本点C1、C2，结合给定的θ值，根据最大最小距离原则确定余下的K-2个聚类中心，然后把样本点分配给距离最近的聚类中心，当数据集中的每个样本点都有确定的一个类别时，聚类结束。参数值θ不同，聚类效果也会有所不同，最后利用avgBWP(k)评价聚类性能，avgBWP(k)值越高，聚类性能越好。

UPK-Means算法流程：

input：数据集X={X1,X2,X3,…,Xn}

output：聚类结果

Step 1：从X中找出距离最远的两个样本点，分别记作C1、C2；

Step 2：计算数据集X中每个样本点到C1、C2的距离Di1、Di2，Di=max{min(Di1，Di2)} ，i=1, 2,…,n。若D1>θ·D12(C1到C2距离) , 则取xi为第三个聚类中心，记作C3=xi；

Step 3：如果C3存在，继续计算Dj=max{min (Di1，Di2，Di3)}，j=1,2,3,…,n,若Dj>θ·D12(C1到C2距离) 则取xj为第4个聚类中心，记作C4=xj，以此类推，直到最大最小距离不大于D12时，寻找聚类中心的计算结束；如果C3不存在，执行Step 4；

Step 4:按照最近原则把所有样本划分给距离最近的聚类中心，从而得到C1,C2,…,Ci个聚类；

Step 5:根据聚类结果，计算每个样本点的BWP值, 然后将BWP值按照从大到小的顺序排列, 选择前96 %的指标值求平均值avgBWP(k)；

在参数θ值的选择上，本文采用等宽分箱思想，将区间[0,1]分成n个区间[0, 1/n]，[1/n, 2/n],[2/n, 3/n],…,[n-1/n,1] ,在每个区间找一个点作为θ值，利用此处得到的n个θ值，然后聚类数据集，使BWP值较小的θ值的区间去掉，将余下的区间继续分成若干区间，直到区间的长度小于规定的值时，迭代过程结束。

3 实验仿真及结果分析

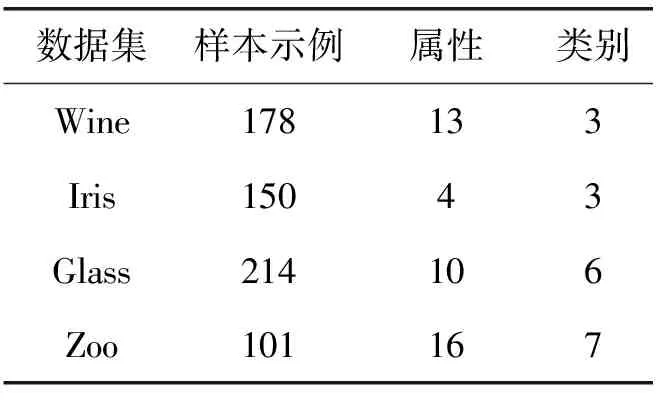
表2 测试数据集基本信息

为了验证本文提出算法的性能，本实验选择UCI数据库中Wine、Iris、Glass、Zoo 4个数据集作为测试数据，实验数据的基本信息见表2，采用Java 语言在WEKA平台中进行仿真实验。

仿真实验时，首先利用最大最小距离找出最远的两个样本点作为聚类中心，继而计算数据集中每个样本点到C1、C2的距离，若D1>θ·D12(C1到C2距离)，则取Xi为第三个聚类中心，记作C3=Xi，依次类推，直到最大最小距离不大于D12时，寻找聚类中心的算法结束，最后按照最近原则对样本进行划分，每个样本都保证分给距离最近的聚类中心，根据得到的聚类结果，计算每个样本点的BWP值, 然后将BWP值按照从大到小的顺序排列, 对前96%的指标值求平均值avgBWP(k)。

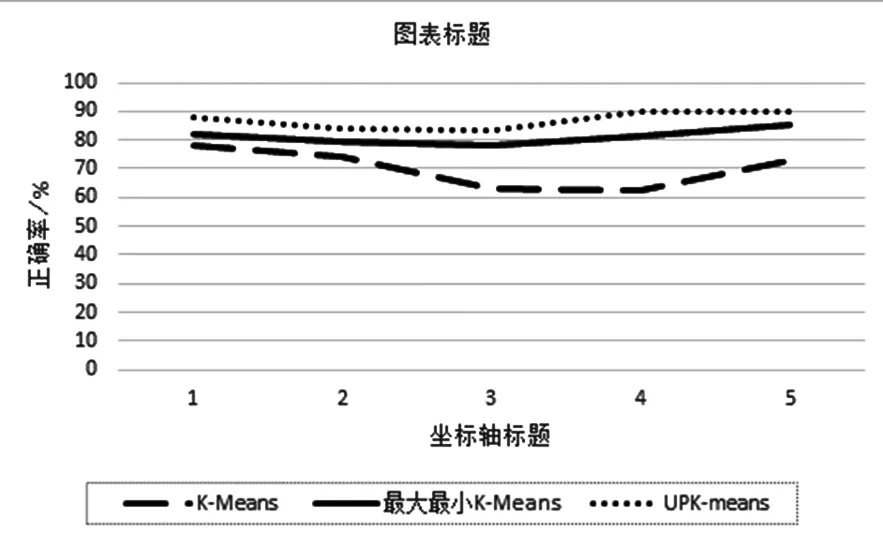
图1 Wine 数据的正确率Fig.1 Correct rate of Wine data

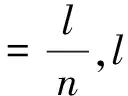
由图1可以看出，对于Wine数据集，使用传统的K-Means聚类结果的正确率相对较低，而采用本文提出的UPK-Means算法后，聚类的正确率得到明显提升。而基于最大最小距离的K-Means算法的正确率处于K-Means算法和UPK-Means算法之间。

为了验证UPK-Means算法的效率，对于其他3组数据集，同样都分别使用K-Means算法、基于最大最小距离的K-Means算法，以及本文提出的UPK-Means进行仿真实验，每个数据集都测试5次，聚类结果的具体信息如表3所示。表中信息为5次测试的平均值。

从表3结果可以看出, 对于Wine、Irish、Glass、以及Zoo数据集传统K-Means算法收敛时间短, 但标准差较大，聚类效果不好, 聚类结果的正确率也较低, 而且传统K-Means算法需要预先指定聚类数目的值。

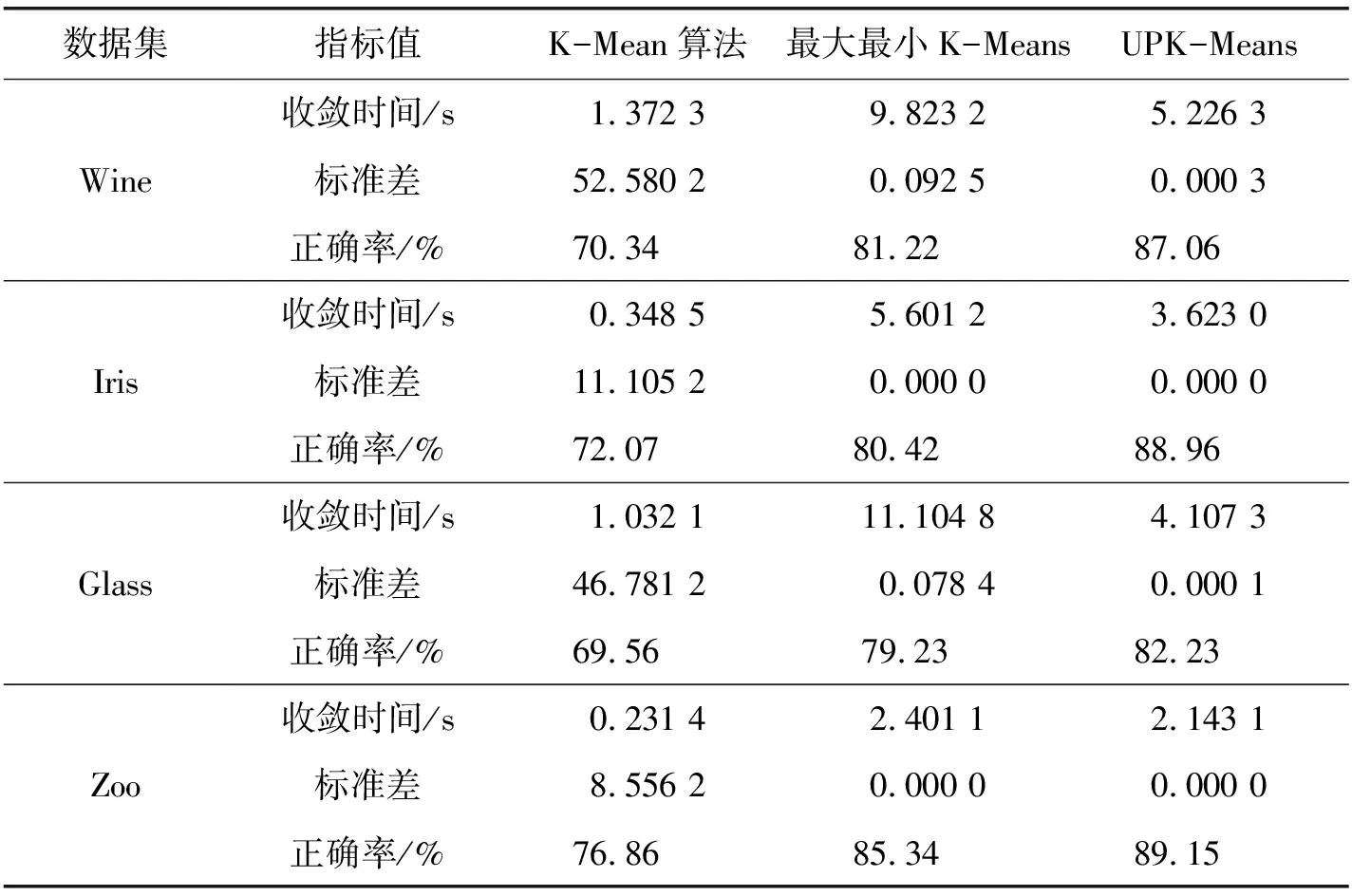
表3 测试数据集的聚类结果

相比K-Means算法、基于最大最小距离的K-Means算法，本文提出的UPK-Means算法从聚类效果的正确率，标准差两方面获得了较好的聚类结果。

4 总结

传统K-Means算法具有算法简单、容易理解、收敛速度快等优点，但使用该算法聚类分析时需要指定聚类数目，而且质心的选择具有不确定性。本文提出一种基于最大最小距离和BWP指标优化的K-Means算法，通过对UCI数据库中的Wine、Iris、Glass、Zoo 4个数据集进行仿真实验，本文提出的UPK-Means算法在算法的准确率、聚类效果两方面均优于传统的K-Means算法以及基于最大最小距离的K-Means算法。