液压挖掘机工作装置结构瞬态动力学分析
2019-11-14李斌
李 斌
(福建船政交通职业学院机械工程系, 福建 福州 350007)
工作装置是挖掘机主构件之一,是挖掘过程中的主要受力部件,其力学性能决定挖掘机整机可靠性和工作性能。对挖掘机工作装置进行结构力学分析,求解工作装置结构应力响应不仅是评价工作装置结构设计是否合理的重要标准,也是工作装置结构优化设计的主要约束条件。但国内挖掘机技术水平、质量、可靠性参差不齐[1]。现有的研究方法在求解工作装置结构响应时普遍存在以下问题:
1)工作装置结构复杂,直接建立结构应力响应模型难度大,求解困难,通过有限元分析计算的方法大大降低了工作装置结构应力响应求解难度,提高了求解精度,但存在有限元建模效率低,人工操作复杂性高等问题[2-3]。
2)许多学者从模型简化和问题降阶等方面研究了有限元建模策略[4-5],降低了建模难度,提高了建模效率,但牺牲了求解精度,且容易形成“人为”应力集中点。
3)目前大部分研究主要以单一构件为研究对象进行结构静强度、静刚度和模态分析,而以工作装置整体为对象开展研究依然较少[6-7]。单一构件为对象进行分析时往往简化了对各构件间连接处的载荷传递问题,导致分析结果准确性较差。
4)现有研究中没有考虑挖掘过程中惯性载荷对工作装置结构性能的影响,结构设计过程中采用降低允用应力的方法考虑惯性载荷的影响,导致工作装置设计结果存在结构笨重、能耗大等缺点[8-9]。
因此,创建挖掘机工作装置整体有限元模型,开展GB9141-88规定的4个工况下工作装置瞬态动力学分析,对于研究工作装置在挖掘过程中结构响应,优化工作装置结构参数,具有一定的理论与现实意义。
瞬态动力学分析是求解随机载荷条件下结构动力学响应的一种方法。ANSYS作为大型通用有限元分析软件,不仅具有强大的瞬态动力学分析计算能力,而且能够与多种CAD软件实现无缝数据连接。ANSYS提供完全法、缩减法及模态叠加法等3种瞬态动力学分析方法。完全法所需分析次数少,但计算开销大。缩减法计算开销较完全法小,但所有载荷必须加在用户定义的主自由度上,适用范围较窄。模态叠加法通过模态分析得到的振型来计算结构响应,虽然分析过程繁琐,但计算开销小,且能够同时得到结构振型和瞬态动力学响应。因此,本文采用模态叠加法计算挖掘机工作装置瞬态动力学响应。
1 基本理论
对于线性结构,瞬态动力学平衡方程如式(1)所示。
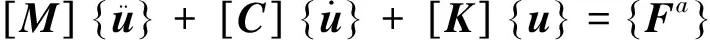
(1)
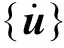
对于该平衡方程,求解方法有完全法、缩减法和模态叠加法。其中,模态叠加法使用坐标转换对平衡方程进行解耦后求解。对模态叠加法,{Fa}可用式(2)表示:
{Fa}=[Fnd]+s[Fs]
(2)
其中,[Fnd]为随时间变化的节点力,s为矢量载荷的比例因子,[Fs]为来自模态分析的载荷矢量。瞬态动力学分析精度取决于积分时间步长,时间步长越小,精度越高。但时间步长过小将浪费计算机资源,降低求解效率。由于结构动力学响应可表示为各阶模态响应的组合,因此,时间步长应足够小以便于求解得到对整体响应贡献最大的最高阶模态。对于Newmark时间积分方案,时间步长取值20倍最高频率。
模态分析用于机械部件振动特性,包括结构固有频率和振型,也可以作为其他动力学分析问题的起点。结构整体动力平衡方程如式(3)所示。
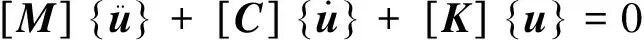
(3)
模态分析方法有分块Lanczos法、子空间法、PowerDynamics法、缩减法、非对称法、阻尼法、QR阻尼法等。
2 有限元模型
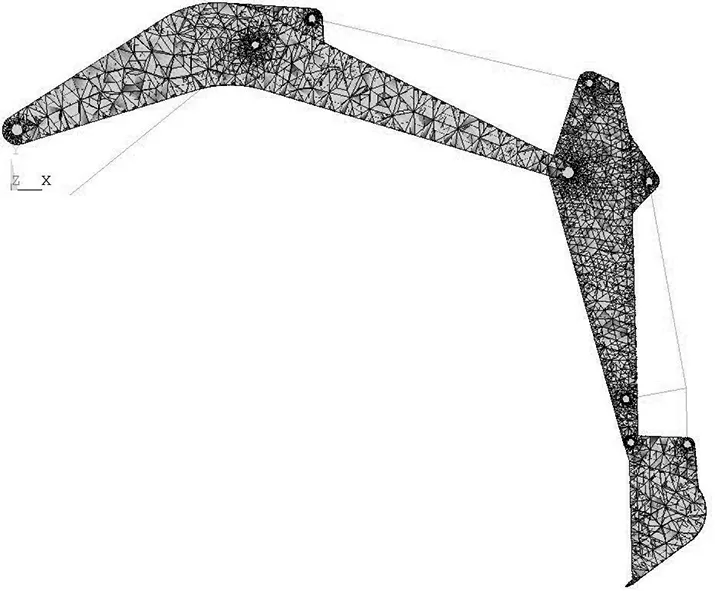
图1 工作装置网格模型Fig.1 Grid model for working device
正确的有限元模型是准确计算工作装置结构瞬态动力学响应的前提。工作装置除含动臂、斗杆和铲斗三大结构件外,还包括动臂液压缸、斗杆液压缸、铲斗液压缸和连杆等部件。工作装置属结构复杂构建,直接在ANSYS环境中构建实体模型或网格模型难度系数高,建模效率低下。而Pro/Engineer软件不仅具有良好的三维实体建模能力,支持参数化建模,建模难度较低,效率高且重用性好,而且与ANSYS环境具有专用无缝数据接口。采用Pro/Engineer创建工作装置模型,导入ANSYS环境后划分得到工作装置网格的方法能够有效提高工作装置网格建模效率。如图1所示为工况2下工作装置的网格模型。为保证挖掘机工作装置获得良好的综合性能,具有较高的强度、塑性,同时具有较好的焊接性能,采用Q235普通碳素结构钢为制造材料。材料的弹性模量E、泊松比μ和密度如表1所示。

表1 工作装置材料属性
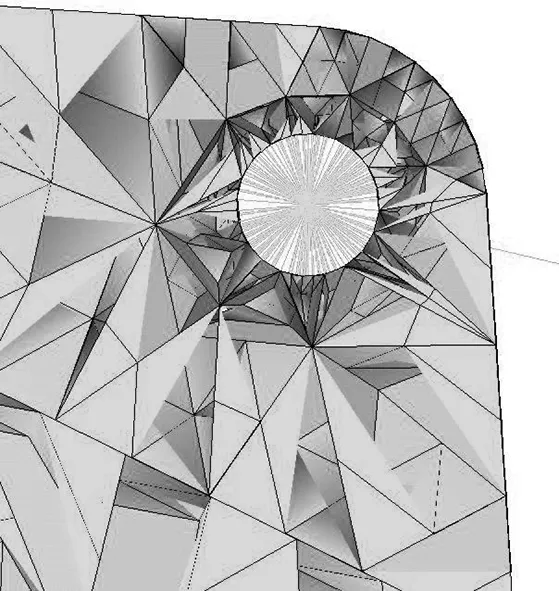
图2 销轴连接有限元模型Fig.2 Finite element model of shaft connection
动臂、斗杆和铲斗等实体采用SOLID95三维实体单元进行网格划分。液压缸、连杆采用LINK8单元进行模拟。工作装置各构件之间的连接采用LINK8和MPC184单元进行模拟。MPC184单元可以模拟刚性杆,刚性梁,滑块,球铰,销轴和万向联轴器等。
如图2所示为动臂与斗杆液压缸铰点处销轴连接有限元模型。为模拟销轴连接,分别在动臂铰孔和斗杆液压缸铰孔中心建立中心节点,中心节点分别与相应铰孔上的节点之间采用LINK8单元连接,而两中心节点间采用MPC184单元实现销轴连接。
3 模态分析
当挖掘机工作频率与工作装置固有频率接近时,将引起共振,使工作装置振动加剧,从而影响工作装置强度和刚度。模态分析的目的是求解工作装置固有频率和振型,从而有效避免工作频率与工作装置固有频率接近。同时,模态分析也是瞬态动力学分析、谐响应分析和谱分析等其它动力学分析的起点。基于GB9141-88规定中4个工况下的有限元模型,可对工作装置进行模态分析。通过模态分析,提取了工作装置前10阶固有频率和振型。如表2所示,为4个计算工况下工作装置前5阶固有频率。
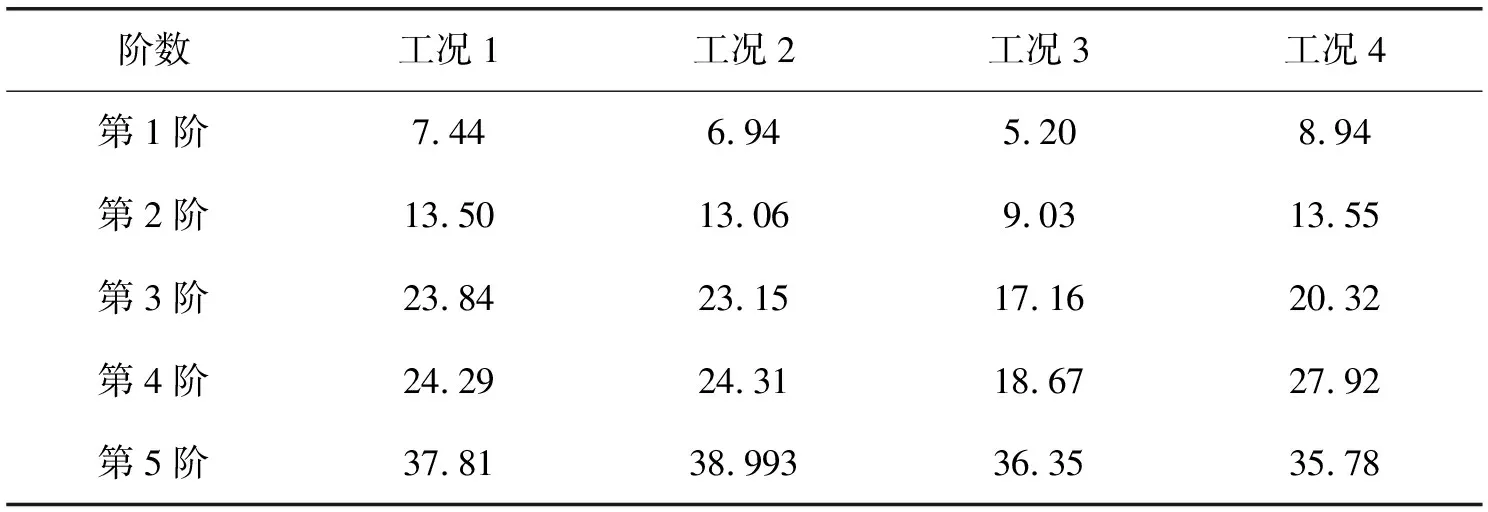
表2 工作装置前5阶固有频率
图3所示为工作装置在工况2下第1阶振型,该振型表现为工作装置在XY平面内弯曲。图4所示为工作装置在工况3下第5阶振型,该振型表现为工作装置在XZ平面内扭转。
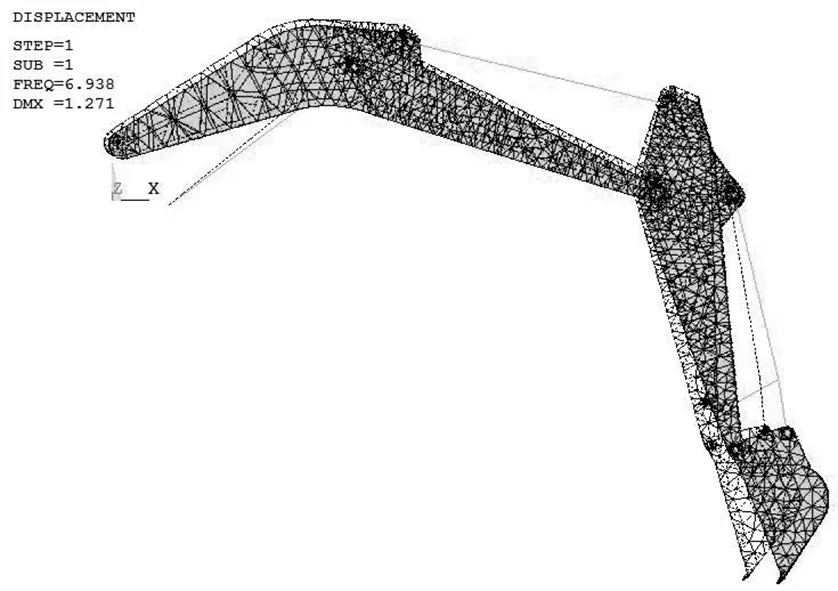
图3 工况2第1阶固有频率振型图Fig.3 Working condition 2, first order natural frequency mode

图4 工况3第5阶固有频率振型图Fig.4 Working condition 3, 5th order natural frequency mode
工作装置模态分析结果表明,不同工况下,工作装置固有频率不尽相同。就结构刚度而言,斗杆和铲斗的刚度较小,受频率影响较大。从各阶振型的角度出发,可知工作装置在各阶振型中主要表现为XZ平面内扭转和XY平面内弯曲。值得注意的是,在工作装置的模态分析中主要考虑铲斗空载的情况,当铲斗满载时,工作装置固有频率将有所不同。
4 瞬态动力学分析
在模态分析的基础上,可采用模态叠加法,通过放大系统后的振型叠加计算工作装置在4个工况下的瞬态动力学响应。在瞬态动力学分析中,单元载荷必须在模态分析中施加。
瞬态动力学分析结果表明,在GB9141-88规定的4个工况下,工作装置最大应力和最大变形出现在第3个工况。如图5所示,工况3工作装置结构最大应力值为177.293 MPa,位于斗杆与铲斗连接铰点处。如图6所示,工况3工作装置结构最大变形量为13.675 mm,位于铲斗齿尖位置。

图5 工况3工作装置应力分布图Fig.5 Working condition 3 working device stress distribution

图6 工况3工作装置变形图Fig.6 Working condition 3 working device variation
如图7所示为工况3下最大应力节点的应力随时间变化曲线。图8所示为变形最大节点变形量随时间变化曲线。由图可知,随着冲击载荷增加,应力值和变形值均随时间呈指数函数变化,直到出现最大应力和最大变形。应力和变形的增加过程为非线性过程,主要是由于在瞬态动力学分析中采用模态叠加法而导致的。
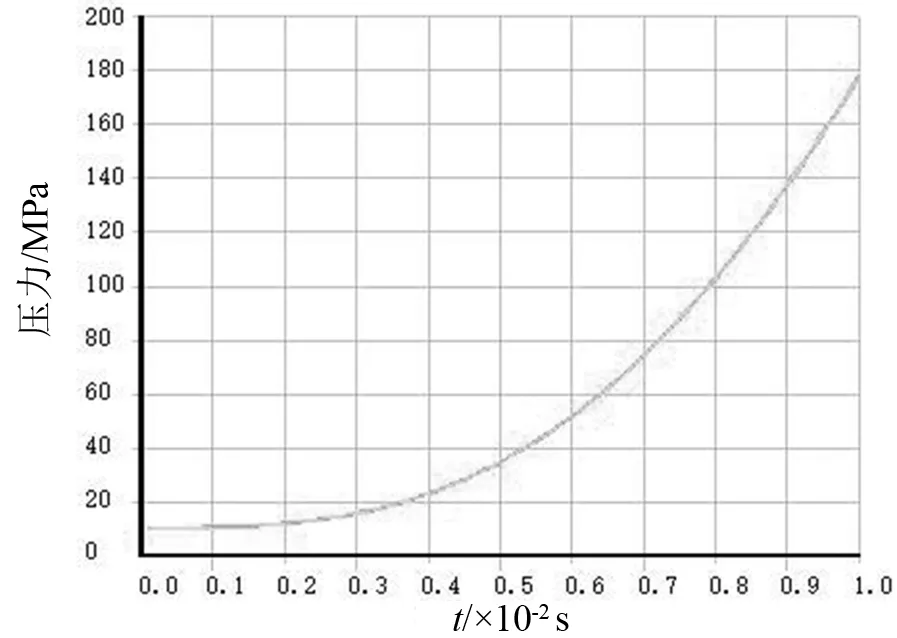
图7 工况3下最大应力节点应力曲线Fig.7 Maximum stress node stress curve under working condition 3
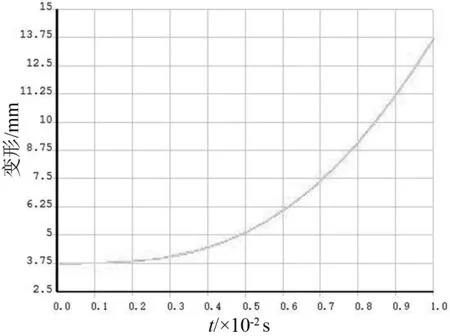
图8 工况3下最大变形节点变形曲线Fig.8 Maximum deformation node deformation curve under working condition 3
5 结论
1)有效建立了工作装置有限元模型,利用LINK8、MPC184单元对液压缸、铰点等局部结构进行了等效处理,保证了有限元模型精度。
2)对工作装置进行模态分析,提取了GB9141-88规定的4种工况下工作装置前10阶固有频率和振型。
3)在模态分析的基础上,基于GB9141-88规定的4种工况,应用模态叠加法对工作装置进行瞬态动力学分析。分析结果表明,最大应力值和最大变形值都出现在工况3上,最大应力值为177.293MPa,位于斗杆与铲斗连接铰点处。最大变形值为13.675 mm,位于铲斗齿尖位置。
