炮弹弹底厚度估算半经验公式*

糜晨曦，王雨时，闻 泉，张志彪，王光宇

(南京理工大学机械工程学院， 南京 210094)

0 引言

弹丸发射时的安全性主要由弹体和其他零件在发射时的强度和刚度来保证。发射时弹体强度计算，实质上就是在求得弹体内各处应力的条件下，根据有关强度理论对弹体进行校核。而弹丸在膛内应校核的是第一临界状态(弹带压力最大)和第二临界状态(膛压最大)时的强度。在第二临界状态下，火药气体压力达到最大，弹底直接承受火药气体压力和惯性力作用。

文献[1]详述了平弹底的传统弹底强度计算公式推导过程，通过简化弹底受力状况，结合弹底弯曲强度分析和第四强度理论，建立了传统弹底强度计算公式(未考虑径向载荷)，并在原形式基础上提出了计算弹底弯曲强度的简化公式。文献[2]在文献[1]的基础上对传统弹底强度计算公式进行了修正(考虑径向载荷)，并增述了变厚度弹底和球形弹底的弹底强度计算公式推导过程，文中就是在传统弹底强度计算公式的修正形式基础上开展弹底厚度估算半经验公式建立工作的；文献[3]指出文献[1]提出的弹底弯曲强度简化公式计算出的最小弹底厚度偏小，因此在文献[1]传统弹底强度计算公式的基础上推算出了粗略的弹底厚度估算公式，文中还结合5种中、大口径弹丸参数验证估算公式的准确性，但其计算出的估算弹底厚度与实际弹底厚度的最大相对误差为24%(大于20%)，验证所用的弹丸种类较少且不包括小口径弹丸，故只能用于粗略计算；文献[4]将枪械的膛内热-结构耦合特性仿真分析引入引信，得到连续发射时火炮内膛膛壁温度对底螺变形有显著影响的结论；文献[5]分析了火炮发射膛内发射药燃烧对弹底引信的影响，得到膛内高温高压燃气瞬态热冲击对弹底引信强度影响可忽略不计的结论；文献[6]分析了弹丸发射时弹底厚度对炸药装药最大等效应变及应变率的影响，发现弹底厚度越薄，炸药装药加载应力率越大，炸药装药的等效应变、应变率越大。

传统弹底强度计算公式虽然具有一定的准确性，但所需的计算参数较多(需7个参数)，公式形式复杂(由21个公式组成)，故其应用受到了一定的限制。例如在弹丸初步设计阶段，弹底厚度的估算、分析和论证就需要更加直观、简便，同时具有一定准确性的经验公式。文中针对此问题，提出了形式简单、所需计算参数少、计算准确度较高的弹底厚度估算半经验公式建立方法。

1 关于传统弹底强度计算公式

在弹丸设计领域，多利用传统弹底强度计算公式来计算弹底危险点的相当应力(第四强度理论)。传统弹底强度计算公式由于没有考虑弹尾区的变形，计算结果有一定误差，但其准确性已经能够满足在弹丸设计领域估算弹底强度的要求。

图1 弹底区的受力情况

平底弹的弹底强度计算公式根据弹底受力情况(如图1所示)，对弹底区进行简化，将弹底看成一块周边受到夹持的圆板，公式包括如下部分[1-2]：

1)计算装填物压力pc

(1)

式中:p为计算膛压，r为弹丸半径，rd为弹底半径，m′ω为弹底面上的装填物质量，m为弹丸质量。

(2)

(3)

式中:md为弹底部分质量，td为弹底厚度，ρm为弹底材料密度。

3)计算弹底与弹体的联系系数K

(4)

(5)

(6)

式中：r0为弹底尾部中性面初始半径，tb为弹底尾部壁厚，β为系数，μ为泊松比(μ取0.3)。

4)计算各危险点的应力和相当应力(考虑对称性，弹底4个危险点位置如图2所示)

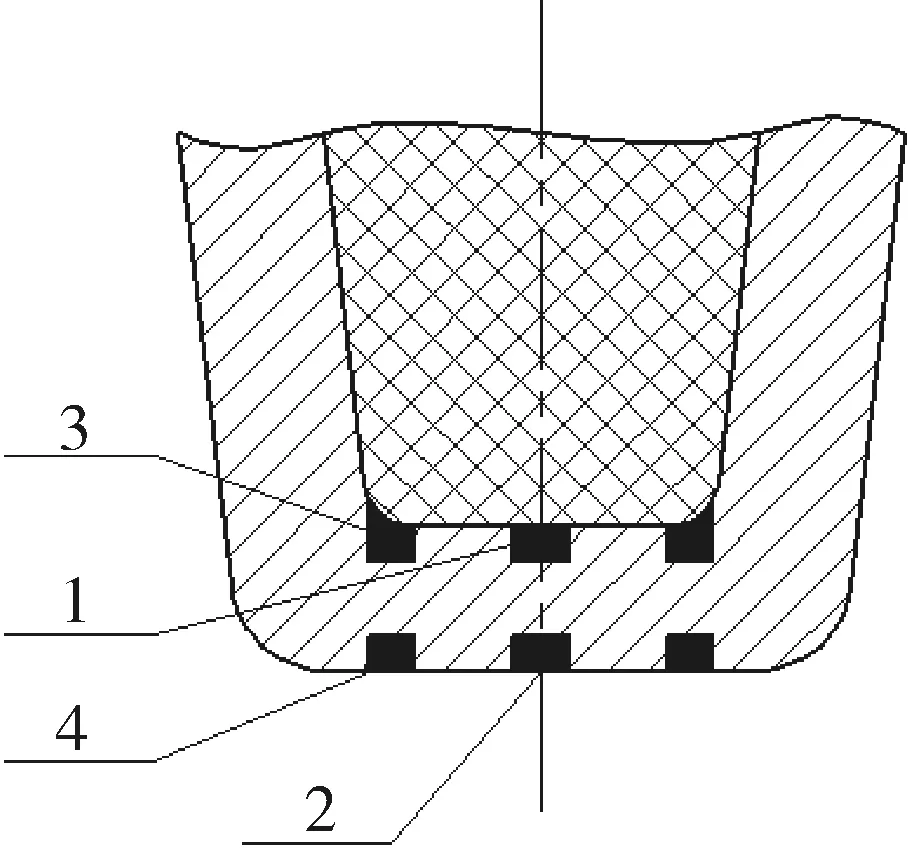
图2 弹底内4个危险点位置

第一点：r=0，z=td/2

(7)

(8)

σz1=-pc

(9)

第二点：r=0，z=-td/2

(10)

(11)

σz2=-p

(12)

第三点：r=rd，z=td/2

(13)

(14)

σz3=-pc

(15)

第四点：r=rd，z=-td/2

(16)

(17)

σz4=-p

(18)

弹底强度用第四强度理论校核，计算上述4个危险点的相当应力：

(19)

最大相当应力为：

(20)

强度条件为：

(21)

2 平底弹的弹底厚度估算半经验公式

在建立弹底厚度估算半经验公式之前，需要先确定半经验公式的适用范围，平底弹适用本公式的前提条件如下：

1)弹丸类型为杀伤爆破弹(榴弹)，且弹底面上的装填物为弹丸主装药，弹底材料为钢。

2)弹丸的计算膛压范围为200～400 MPa。

3)发射产生的火药燃气压力直接作用在整个弹底面上。

以上3个适用条件中，条件1)排除了发烟弹、照明弹、宣传弹、穿甲弹、破甲弹和碎甲弹等弹丸类型，条件2)排除了无后坐炮弹、迫击炮弹和火箭弹等低过载弹丸，条件3)排除了尾翼弹和弹底带曳光管的弹丸。

根据弹底厚度估算半经验公式的适用条件，选择了满足条件的15个弹种作为样本，表1列出了这些弹丸在弹底强度计算中所需要的参数。

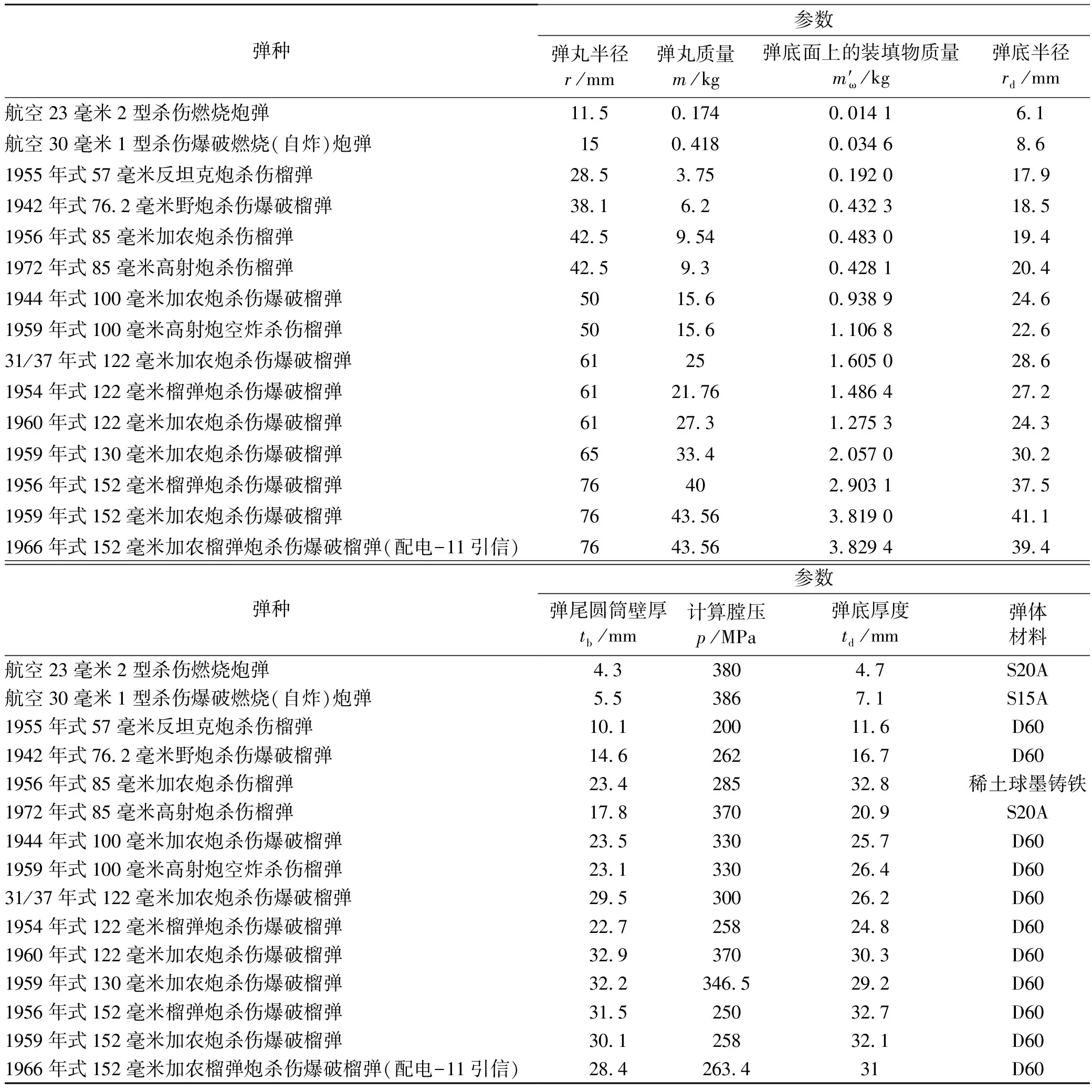
表1 弹底强度计算中所需的弹丸参数[7-8]

由于传统弹底强度计算公式用到的参数较多，计算过程复杂，所以将建立弹底厚度估算半经验公式的过程分为4个步骤：

(22)

(23)

式中:k1、k2为常系数，无量纲量。将表1参数代入式(1)、式(2)、式(3)、式(22)及式(23)计算可得，经验系数k1的变化范围为0.548 4～0.808 3，取各弹丸k1的平均值0.622 7，经验系数k2的变化范围为0.129 8～0.364 7，取各弹种k2的平均值0.276 3。

2)简化弹底与弹体的联系系数K计算公式。联系系数K为无量纲量，由rd、tb、td决定。将表1参数代入式(4)、式(5)和式(6)计算可得，联系系数K的变化范围为0.205 2～0.530 3，取平均值0.408 2。

(24)

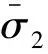
(25)

(26)

式(26)改写为

(27)

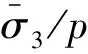
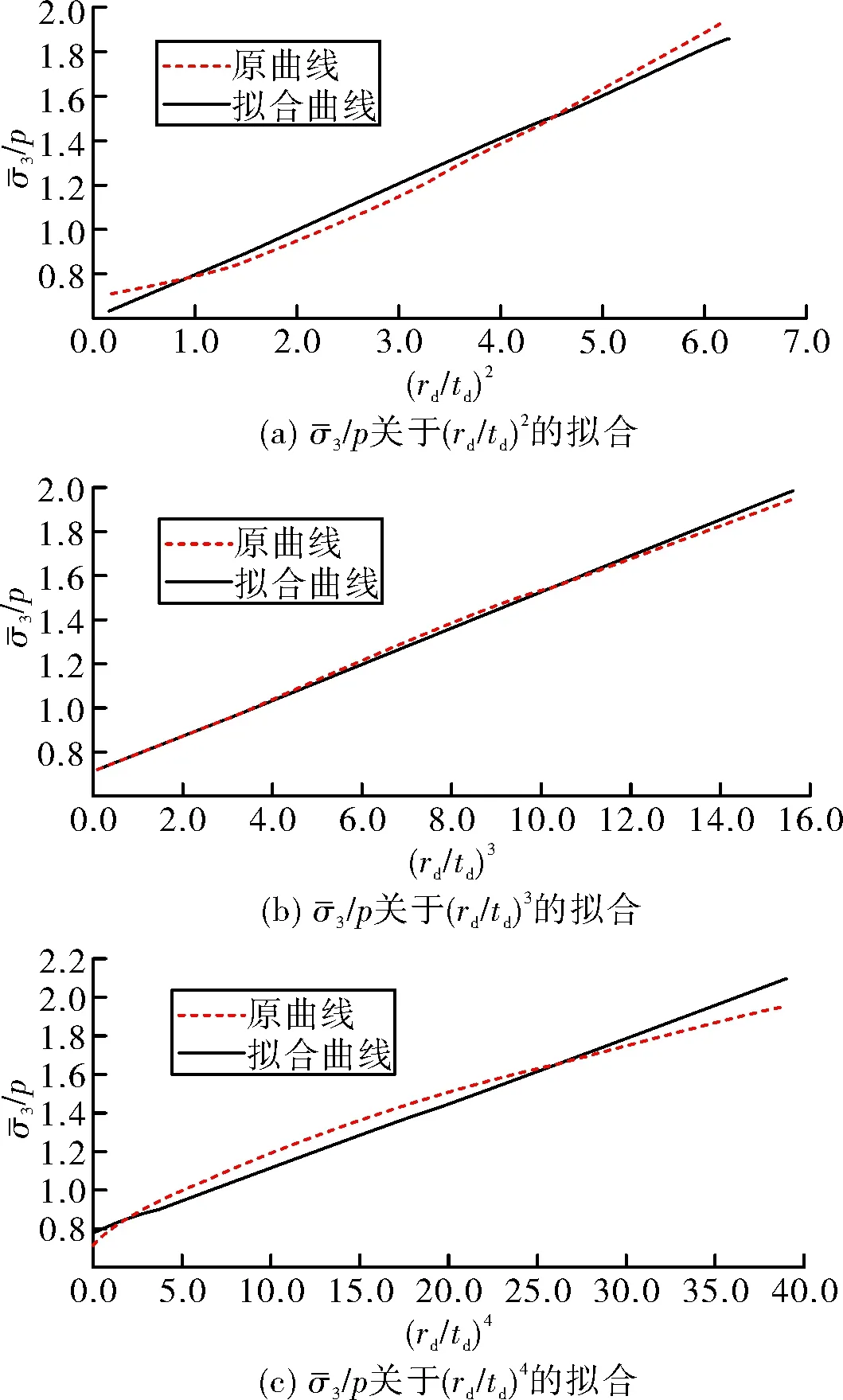
图关于(rd/td)2、(rd/td)3以及(rd/td)4的拟合结果

(28)

(29)

已知材料屈服强度σ0.2的情况下，可以利用传统弹底强度计算公式和简化半经验公式计算出最小弹底厚度。选取15种弹丸中弹体材料为D60、S15A和S20A的14种，取弹体材料D60、S15A和S20A的屈服强度σ0.2分别为350 MPa、460 MPa和500 MPa，计算出传统弹底强度计算公式和简化半经验公式的最小弹底厚度和与实际弹底厚度的相对误差，发现传统弹底强度计算公式和简化半经验公式计算出的最小弹底厚度与制式弹采用的实际弹底厚度偏差较大，而制式弹采用的实际弹底厚度是经过设计计算和射击试验综合考量得到的，实际弹底厚度应接近(略大于)真实的最小弹底厚度。因此需要对简化半经验公式进行修正，以减小半经验公式计算出的最小弹底厚度相对于实际弹底厚度的偏差。实际弹底厚度不仅仅是理论计算得到的结果，而是结合了产品设计等因素考虑的结果，用这个参数来衡量传统弹底强度计算与弹底厚度估算半经验公式的优劣有一定的偏差，但该偏差使半经验公式的计算结果趋于保守，利于保证设计弹丸的安全性。

(30)

依据最小二乘法原理，以弹体材料为D60、S15A和S20A的14种弹丸的实际参数计算值(rd/td)3和σ0.2/p为样本，运用Matlab软件，对β1在0～10，β0在-35～2的范围内，以实际值与计算值的离差的平方和最小为优化判据，进行局部寻优，根据Matlab软件的拟合结果，可得到平底弹的弹底厚度估算半经验公式：

(31)

用新的弹底厚度估算半经验公式计算各弹丸的最小弹底厚度，并计算半经验公式得到的最小弹底厚度相对于实际弹底厚度的相对误差，计算结果如表2所列。

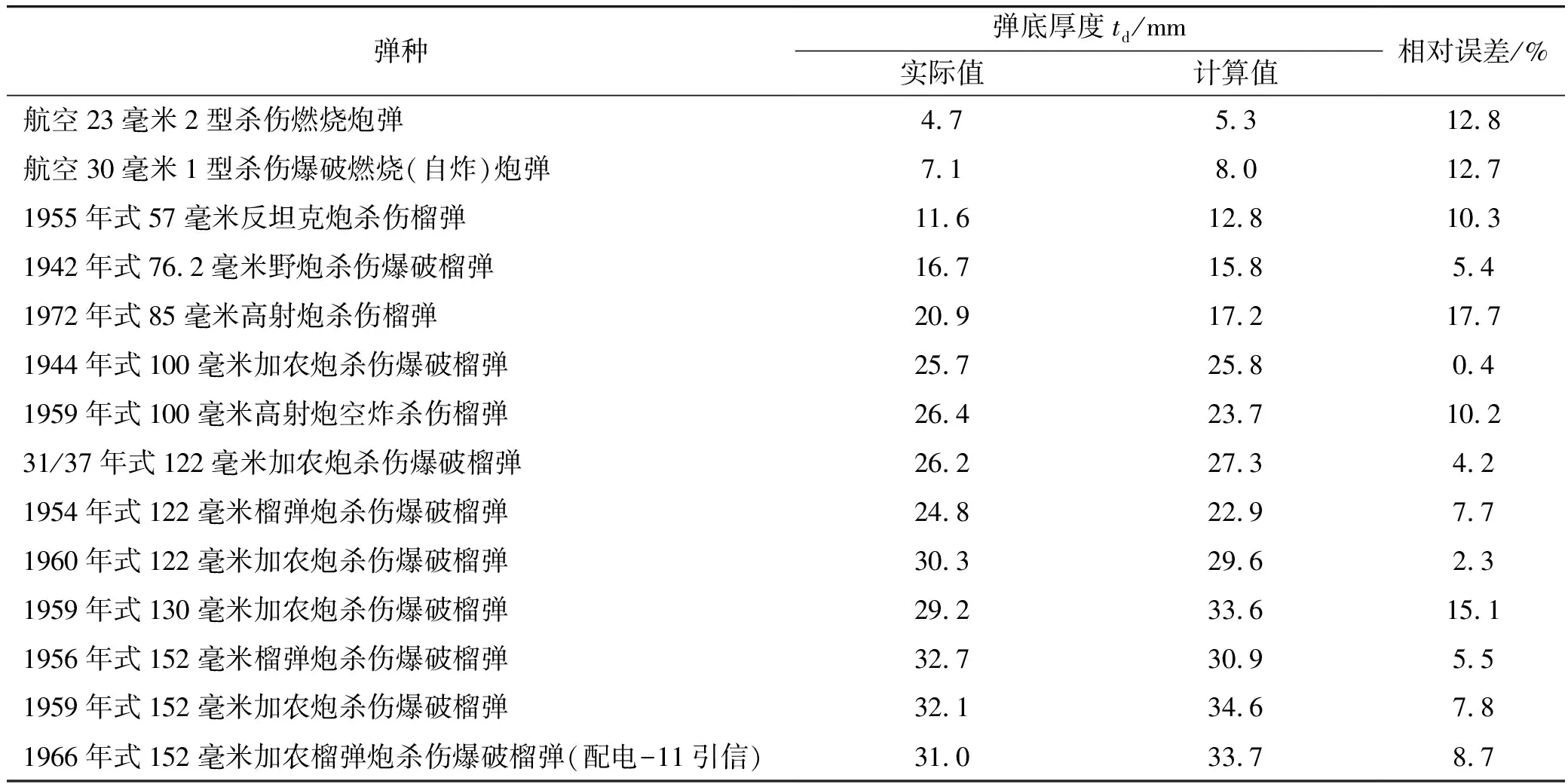
表2 弹底厚度估算半经验公式的弹底厚度计算结果

由表2可知，相对误差平均值为8.6%(小于10%)，最大相对误差为17.7%(小于20%)，满足弹丸工程设计的要求。

最终得到炮射平底弹丸按发射强度设计时的弹底厚度估算半经验公式：

(32)

弹底厚度估算半经验公式拟合所用到的样本参数σ0.2/p=0.95～1.75，因此弹底厚度估算半经验公式的适用条件为σ0.2=(0.95～1.75)p。根据式(32)，当σ0.2/p→0.95时，td→1.21rd；当σ0.2/p→1.75时，td→0.71rd；当σ0.2/p→1时，td→1.13rd；当σ0.2/p→1.4时，td→0.82rd，通常有σ0.2=(1.0～1.4)p，故

td≈(0.82～1.13)rd

(33)

在σ0.2/p=0.95～1.75以外，当σ0.2/p→+时，td→0；当σ0.2/p→0.75时，td→+。说明式(32)外延至σ0.2/p=0.95～1.75以外，基本规律依然成立。

3 仿真验证和结果分析

为了验证推导出的平底弹的弹底厚度估算半经验公式的可信性，以1959年式152毫米加农炮杀伤爆破榴弹为例，利用有限元软件ANSYS结构静力学模块，数值模拟弹丸弹尾区在p、pc和惯性力作用下的应力应变状况。

根据弹尾区的结构和受力对称性，可以将其简化为四分之一模型。由于弹尾区和弹体交界处情况复杂(弹带槽、弹带和弹带压力等因素影响)，因此在仿真中假设弹尾区和弹体交界为固定约束，而该假设与实际情况有一定偏差。根据圣维南原理，该假设会导致仿真得到的靠近弹尾区与弹体交界处的弹壁区域应力状况失真，而远离交界处的弹底部受到的影响较小，表现为弹底部第三危险点处相当应力偏小，而弹尾区第二危险点处相当应力偏大。该仿真的主要目的是对比不同弹底厚度下弹底部的应力状况，不需要考虑弹壁的应力状况，且该偏差对不同弹底厚度下弹底部应力状况的影响是相同的，因此对不同弹底厚度下弹底部应力状况对比结果的影响可以忽略不计。

以1959年式152毫米加农炮杀伤爆破榴弹为例，已知1959年式152毫米加农炮杀伤爆破榴弹的计算膛压p为258 MPa，取装填物压力pc为77.3 MPa，弹尾整体加载沿弹轴向上的惯性加速度为107 500 m/s2。弹体材料为D60，其材料特性如表3所列。

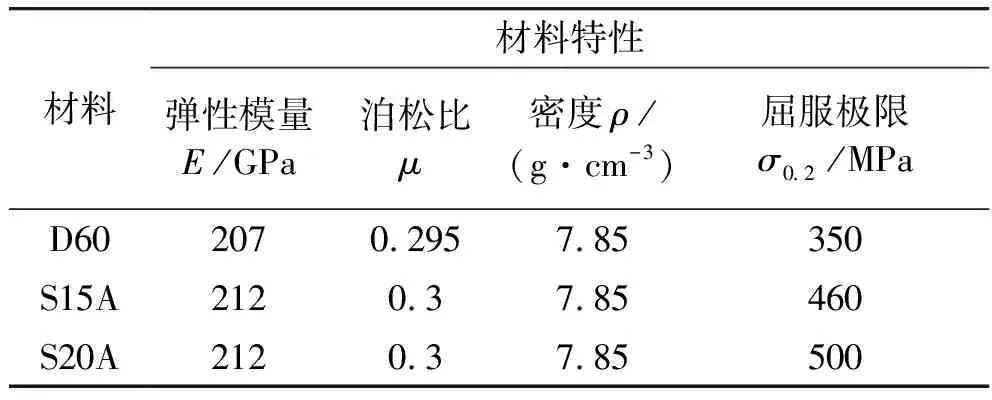
表3 常温下D60、S15A和S20A钢的材料特性[9]

对表2中的14种弹丸进行有限元仿真计算，利用有限元软件仿真得出第二、第三危险点处最大相当应力情况；根据传统弹底强度计算公式计算结果修改14种弹丸的弹底厚度，利用有限元软件仿真得出第二、第三危险点处最大相当应力情况；根据半经验公式计算结果修改14种弹丸的弹底厚度，利用有限元软件仿真得出第二、第三危险点处最大相当应力情况。结果如表4所列。

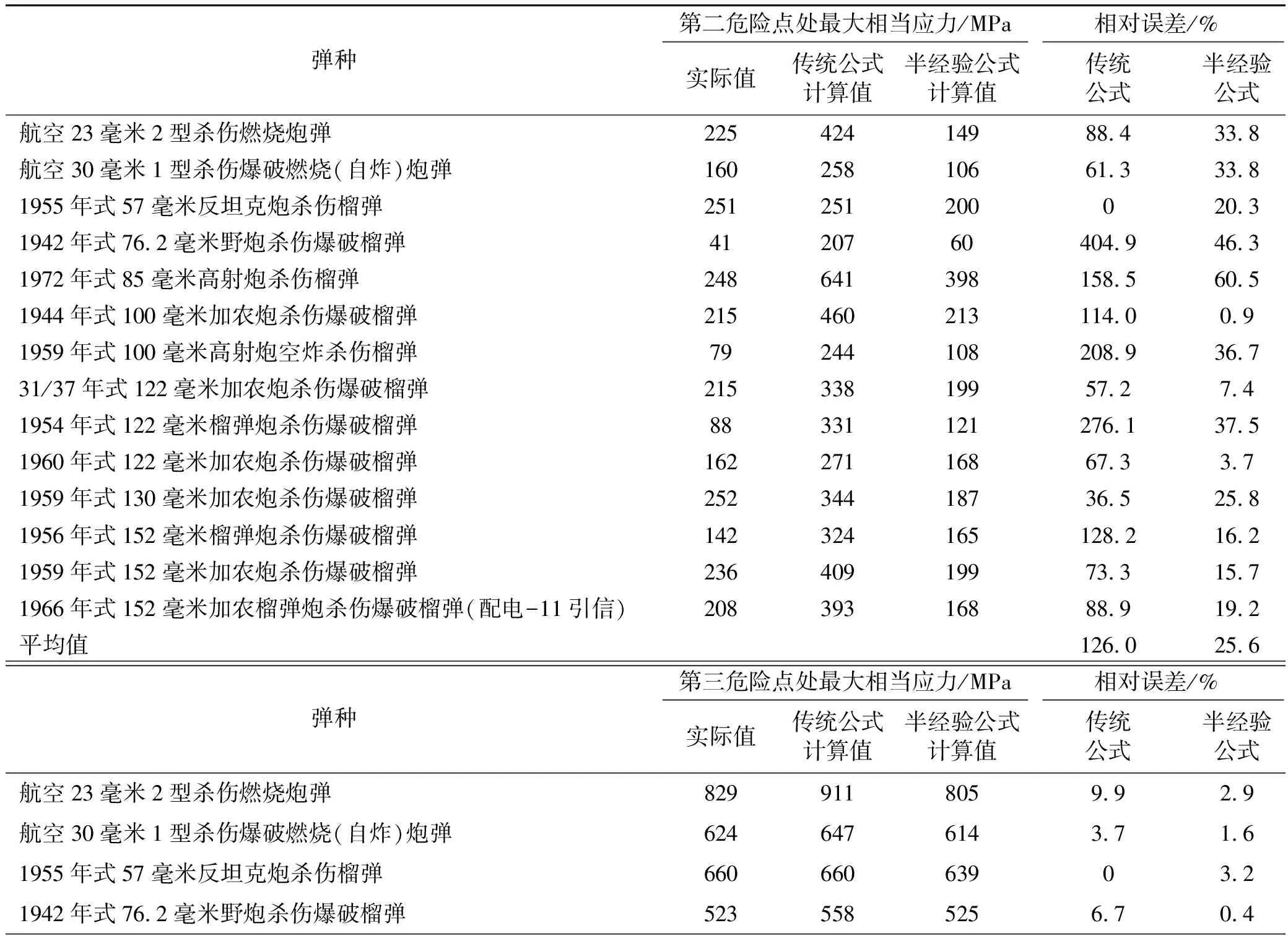
表4 有限元软件计算得出的最大相当应力情况

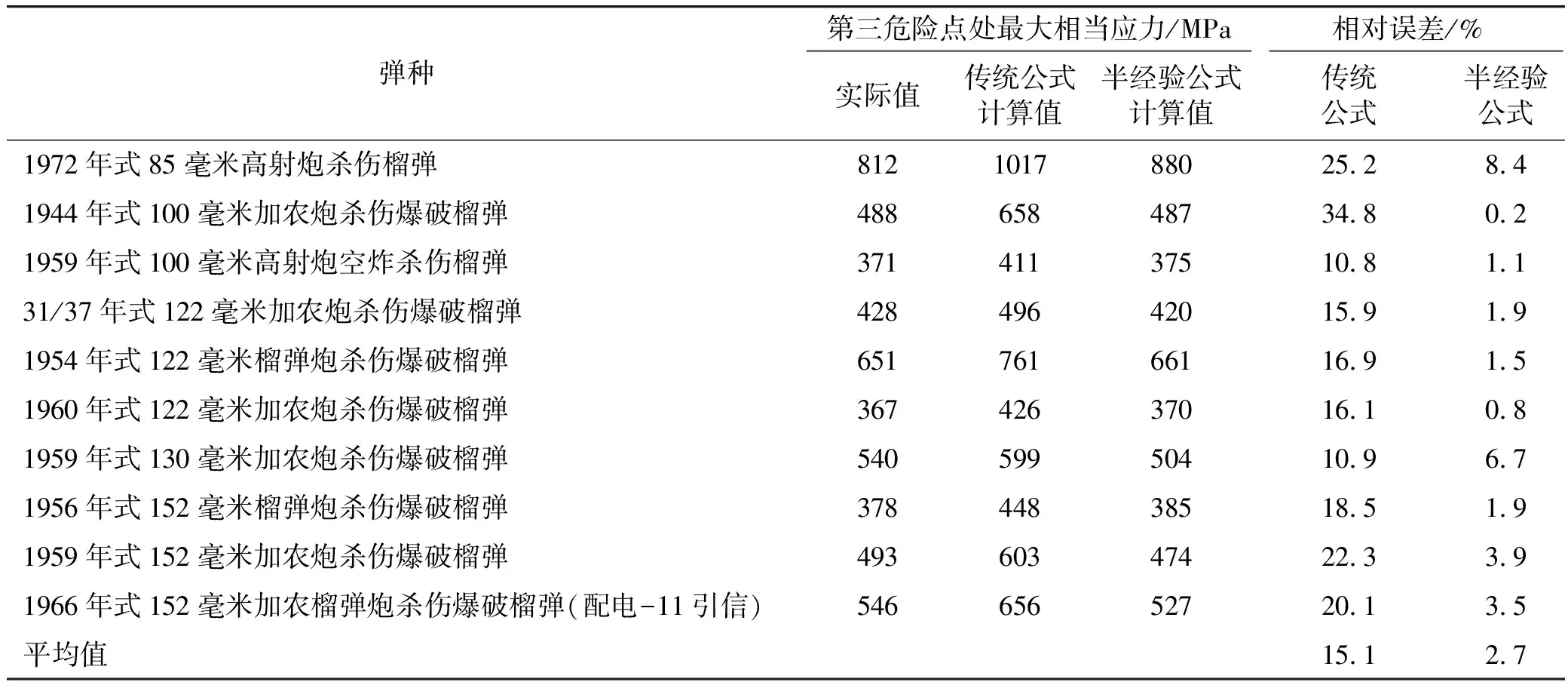
续表

由有限元计算的结果可以得到如下结论：

1)弹底的第三危险点处的确有明显的应力集中现象，弹底部的最大相当应力也均发生在第三危险点处，这一点符合之前的假设。

2)与实际弹丸弹尾区的应力分布相比，由传统弹底强度计算公式计算出的弹丸弹尾区的应力分布状况明显更加恶劣，第二、第三危险点处的最大相当应力明显偏大，第三危险点处发生塑性变形的区域范围扩大。

3)由弹底厚度估算半经验公式计算出的弹丸弹尾区的应力分布状况与实际弹丸弹尾区的应力分布状况相似，第二、第三危险点处的最大相当应力相差也不大，验证了半经验公式计算结果的准确性优势。

4 结论

文中提出了形式简单(文中给出的半经验公式只有1个公式)、所需计算参数少(文中给出的半经验公式只需3个参数)、计算准确度较高(相对误差平均值为8.6%，最大相对误差为17.7%)的弹底厚度估算半经验公式的建立方法。该方法基于传统弹底强度理论，利用满足公式适用条件的各种弹丸的参数建立传统弹底强度计算公式的简化形式，结合最小二乘法原理，通过局部寻优，拟合得到能够满足弹丸工程设计要求的弹底厚度估算半经验公式。公式是在对现有产品总结和验证基础上得出的，只适用于平底炮弹。仿真结果表明，与传统弹底强度计算公式相比，由弹底厚度估算半经验公式计算出的弹丸弹尾区的应力分布状况与实际弹丸弹尾区的应力分布状况更相似，验证了弹底厚度估算半经验公式计算结果的准确性优势。