基于多层蒙特卡罗的火箭结构动力学不确定性分析*

袁 赫，刘 莉，康 杰

(1 北京理工大学宇航学院， 北京 100081； 2 飞行器动力学与控制教育部重点实验室， 北京 100081)

0 引言

在运载火箭结构动力学响应分析过程中，存在诸多不确定性，例如外载荷的不确定性、建模时模型的不确定性，这些不确定性因素是客观存在的，粗略地忽略这些不确定性因素会造成分析误差。

由于运载火箭结构复杂，目前运载火箭结构动力学响应分析主要采用有限元方法[1]。不确定性分析方法主要分为非采样方法和采样方法。非采样方法包括泰勒展开法[2]、区间摄动法[3]、随机伽辽金法[4]等，这些方法虽然高效，但受算法侵入性的局限，对于运载火箭这种大型复杂结构来说适用性差。为考虑复杂结构分析中的不确定性，可将有限元方法和采样方法结合，经典例子是对有限元模型进行蒙特卡罗(MC)仿真[5-6]，后续出现的拟蒙特卡罗法[7]、马尔科夫蒙特卡罗法[8]是MC方法的延伸，由于MC方法的非侵入性，使其成为了大型有限元结构不确定性分析简单有效的方法。但大型有限元结构的结构动力学响应分析代价往往较高，尤其是对带有多个不确定性变量且计算精度要求高的问题，MC方法的计算代价将无法接受。

多层蒙特卡罗方法(MLMC)是基于方差减小的思想降低计算代价的一种期望估计方法，起先用来求解带有随机参数的偏微分方程[9]，后续成功的与有限元方法结合应用到工程结构的静力学[10]、热力学[11]、可靠性[12]的不确定性分析中，提高了计算效率，但在运载火箭结构动力学不确定性分析领域还鲜有应用。

文中将MLMC方法引入运载火箭结构动力学不确定性分析中，结合有限元方法，以某一具有较大长径比助推器的捆绑式运载火箭为研究对象，分析了带有模型不确定性的运载火箭结构在点火起飞工况下的捆绑连杆动力学响应，与MC方法相比，MLMC方法计算效率有显著的提高。最后，给出了捆绑连杆动响应的统计特性，为运载火箭初步设计阶段的强度分析和结构设计提供基础。

1 不确定性分析方法

1.1 蒙特卡罗仿真

MC方法求解不确定性问题的基本思想是：构造一个概率模型或随机过程，使问题的解等于其参数，然后生成N个服从一定分布规律的采样点，计算采样点响应的统计特性，响应期望由式(1)估计：

(1)

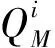
MC估计方法的误差来源于两种，一种是由有限元网格数量引起的系统误差，对于每个采样点来说随着有限元模型自由度数M的增加，其估计值收敛于真值，即

|E[QM-Q]|≤C1M-α

(2)

式中:α为收敛阶数，C1为依赖于M的常数。

第二种误差为受有限次采样数量影响的采样误差，则总误差可以用均方误差表示如下[13]:

(3)

由式(3)可知，为了减小估计误差，最直接的方法是提高采样数量或者增加有限元模型网格数量，但是对于大型结构的结构动力学响应分析来说，这两种途径会造成难以接受的计算代价。

1.2 多层蒙特卡罗仿真

中心极限定理证明MC方法提高计算效率的有效方法之一是减小样本点响应的方差。MLMC方法正是一种基于方差减小的思想来提高计算效率，它通过不同有限元网格数量的模型组合来估计目标值期望。依据有限元网格数量的精细程度，模型可划分为0到L级，每层模型在每个维度上的网格尺寸比上一层模型精细，精细倍数为K，文中将K取为2，如图 1所示的板结构层级有限元模型。

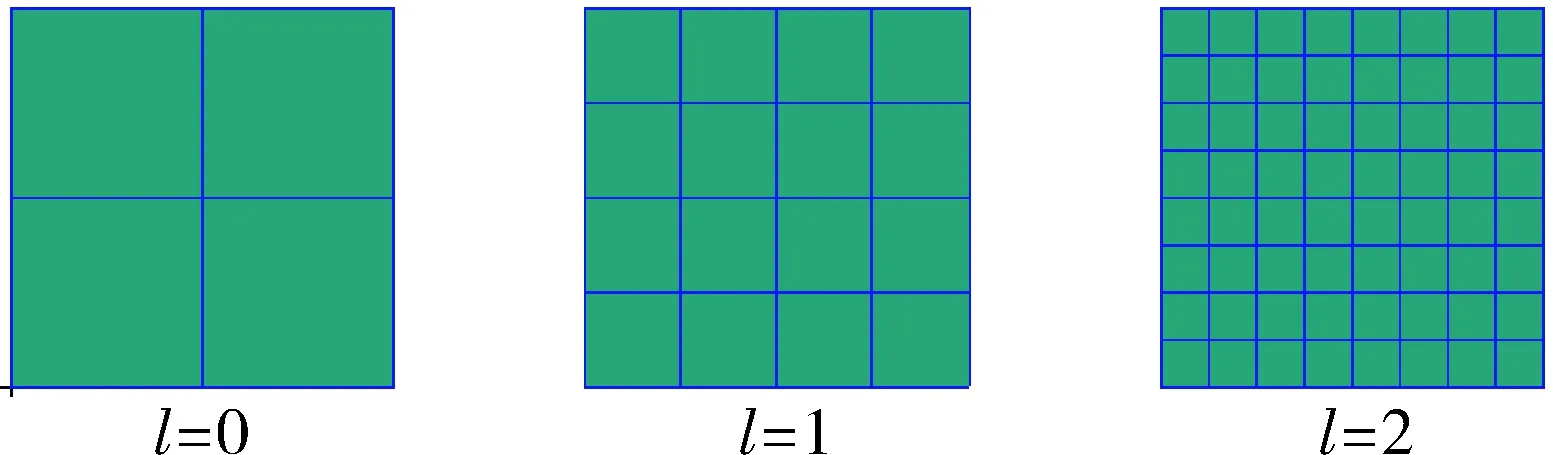
图1 板结构层级有限元模型

利用期望算子的线性特性，L层模型目标值期望可以表示成0层模型目标值期望加上连续层级模型目标值之差的期望，即

(4)

等式右侧的无偏估计为：

(5)

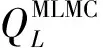
假设式(5)中的每层标准蒙特卡罗估计是独立的，则该估计的均方误差可以表示为:

(6)

式中：Vl=Var[Yl]。

为了使均方根误差小于给定误差ε2，可使式(6)第一项采样误差和第二项系统误差均小于0.5ε2。在采样误差的既定要求下，同时使计算代价最小，该问题可以转化为如下数学问题:

(7)

式中：Cl为计算一次Yl的计算代价。

采用拉格朗日乘子法，将Nl视为连续变量，从而得到每层模型最优采样数量。

(8)

随着模型层级的增加，Ql和Ql-1收敛于真值Q，因此

(9)

式(8)表明采样数量Nl是l的减函数，也就意味着多层蒙特卡罗估计的采样数量集中在低层模型也就是计算代价小的模型上。

式(6)第二项系统误差决定了模型的最高层级L，假设|E[Yl]|的收敛速度的阶为O(K-α)，则

(10)

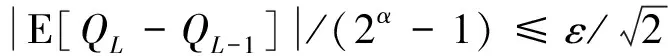
1)|E[Ql-Q]|≤C12-αl；

2)Vl≤C22-βl；

3)Cl≤C32γl。

因此，存在一个正数C4，对于任意ε≤e-1，存在最高层级L和相应的采样数量使得多层蒙特卡罗估计的均方误差小于给定误差，并且计算代价有界，如式(11)所示。

(11)

2 运载火箭模型建立

运载火箭建模方法主要有3种：集中质量-梁建模方法、局部三维建模方法、三维建模方法。其中集中质量-梁模型和局部三维模型针对实际结构做了大量的简化，而三维模型能更好的模拟运载火箭结构的刚度特性，尤其是对于超静定结构，能更好的模拟捆绑结构的传力情况[14]。文中基于Nastran建立运载火箭三维有限元模型，模型数据引用文献[15]，芯级全长52 m，直径3.35 m，4个助推器全长26 m，直径2.25 m，芯级与助推器之间采用前、中、后3个捆绑结构，以下分别叙述各部分结构建模方法。

2.1 主体结构建模

这里的主体结构指运载火箭整流罩、级间段、助推器等部段，大部分为薄壁加筋结构。为了简便起见，这里采用当量厚度的薄壳来模拟，建模原则为拉压、弯曲、扭转刚度与原来相同。在建模时首先在站点处建立结构质量点，四周按照箭体半径布置相应的壳单元，质量点与壳之间采用RBE3单元连接，将集中质量平均分配到壳上。

2.2 液体推进剂建模

由于液体推进剂没有刚度，建模时只需模拟其质量特性。贮箱横向弯曲变形时，因液体推进剂无黏性，推进剂不会随着贮箱壁面一起转动；在贮箱纵向变形时，液体只跟随箱底一起运动。因此，建模时将贮箱节点附近的推进剂按集中质量法等效到该节点上，纵向质量效应只作用在贮箱底部节点上，横向质量效应作用在贮箱的各个站点，贮箱柱段和贮箱下底节点的耦合质量矩阵分别为式(12)和式(13)[14]。

(12)

(13)

其中∑me为贮箱内推进剂总质量；me为节点附近区域推进剂质量。

2.3 捆绑连接结构建模

捆绑连接结构是捆绑式火箭非常重要的连接方式，文中模型采用三捆绑连接方式，图 2(a)给出了由3根连杆(两根直杆，一根斜拉杆)组成的前、中辅助捆绑结构。建模时首先确定杆在助推器上的连接中心，依据杆的空间角度确定芯级的连接中心，在两个连接中心之间建立杆单元。为避免捆绑连接处的刚度过于薄弱，在芯级和助推器捆绑点处建立加强框，杆的连接中心用RBE2单元固接到加强框上。主捆绑是典型的球头-球窝结构，中间没有转动约束，建模时采用两根梁单元模拟球头和球窝，两根梁采用多点约束连接，并释放转动自由度来模拟转动效应。加强框的刚度一般由地面点火实验确定，在运载火箭设计初期，该结构的刚度不能准确的给出，只能凭经验给出一定的范围，具有较大的不确定性。

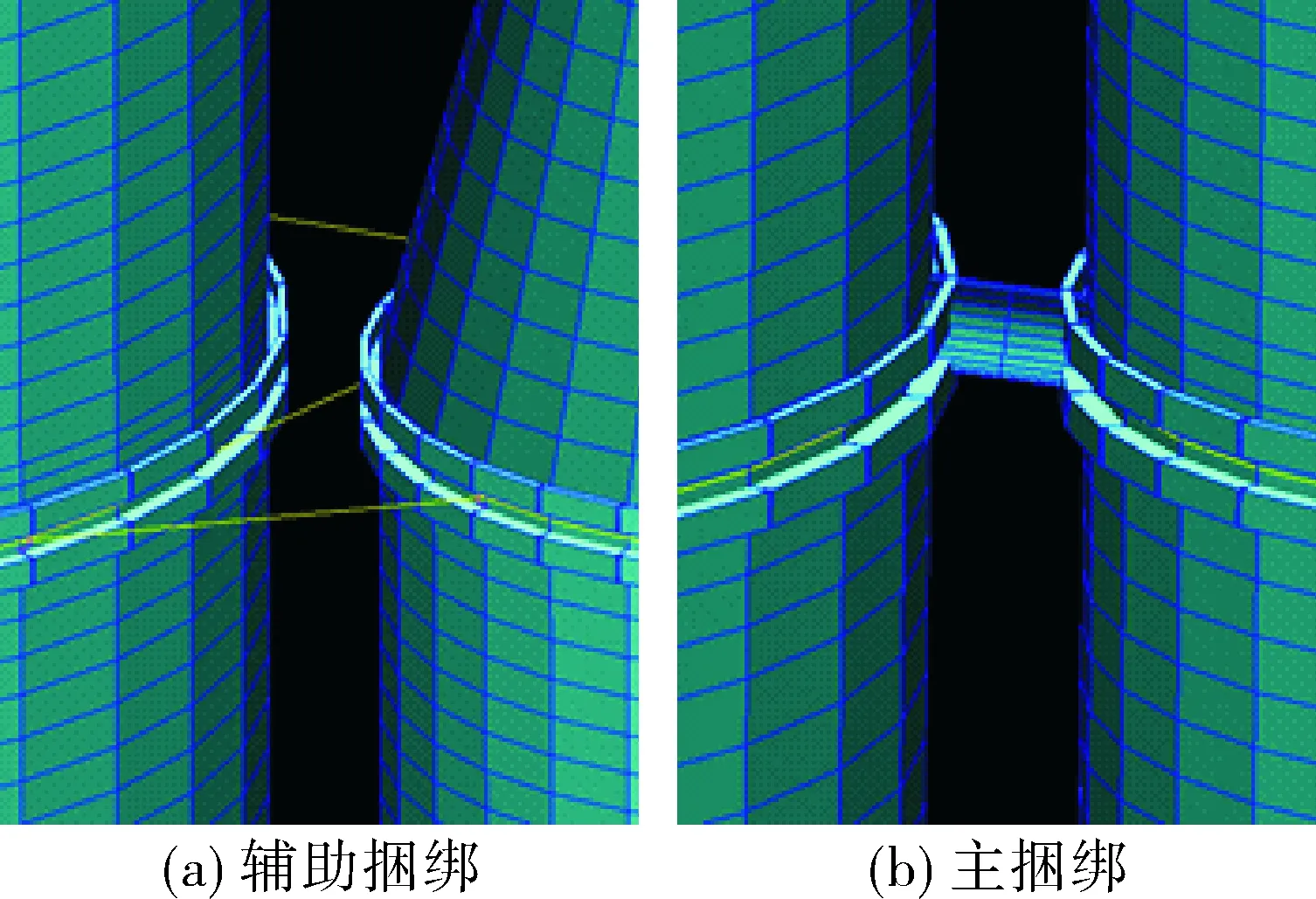
图2 捆绑连接结构

2.4 发动机结构建模

发动机结构包括发动机支架及发动机本身，发动机支架的作用是将发动机推力传递到火箭上。建模时首先确定发动机的质心位置，在该位置和发动机对接面站点之间建立梁单元模拟支架，支架质量等效到发动机上。对于发动机本身来说，由于文中分析的是关于全箭整体的工况，不需要发动机复杂的结构形式，建模时采用集中质量单元模拟其质量特性即可，建立原则为其质量大小和位置与真实结构相等。依据上述建模方法，运载火箭的三维模型如图 3所示。

3 结构动力学不确定性分析

3.1 计算工况

文中的研究对象为带有四助推器的超静定捆绑运载火箭三维模型，计算工况为竖立在发射台上时发动机点火时刻，发动机开机曲线采用50吨级氢氧发动机开机试验数据[16]，对全箭做瞬态响应分析，计算捆绑连杆中受载情况最严苛的中捆绑直杆的动响应(轴力)极值。不确定性变量为辅助捆绑点的加强框刚度，服从均值为7.4×1011Pa，标准差为1.51×1011Pa的正态分布。

3.2 多层蒙特卡罗应用思路

1)模型层级划分

按1.2节给出的层级模型网格细化方法，将运载火箭三维模型分为4个等级(L=3)，每一层级模型两个站点间的四边形网格在径向和轴向较上一层级细化2倍。表 1列出了各层级模型每两个站点间网格数量，图 3给出了各层级火箭有限元模型。

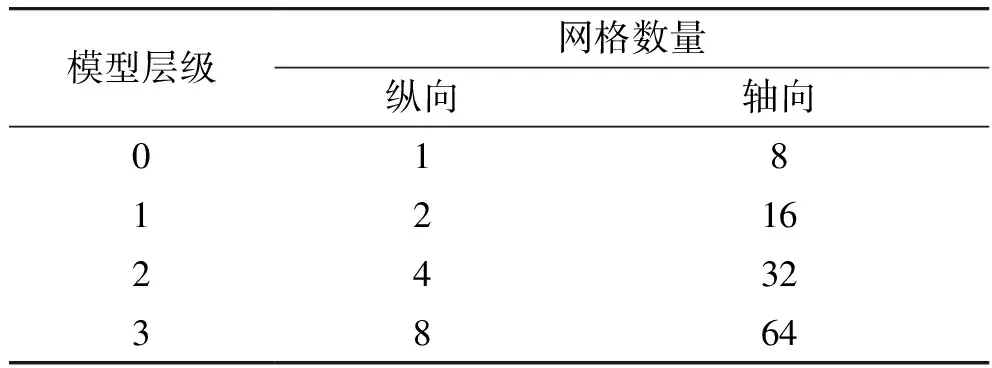
表1 层级模型网格数量

图3 运载火箭层级有限元模型

首先，加强框刚度取均值对各层模型做开机工况计算。图 4给出了Cl的变化情况，其对数值正比于2γl，参数γ取决于计算机性能，这里γ≈2.4。橙色图线为各层模型的中捆绑直杆的动响应极值，随着模型层级的增加，网格的不断细化，该值趋于收敛，从工程应用的角度来说，最高层级L=3已经足够精确。

2)具体实施步骤

步骤一：给出每层模型初始采样量N0，随机生成N0个服从正态分布的加强框刚度，按生成的刚度修改模型；

步骤二：从l=0开始计算Ql、Ql-1，当l=0时Ql-1=0；

步骤三：计算方差Vl=Var[Yl]；

步骤四：根据式(8)计算每层模型最优采样数量Nl；

步骤五：定义ΔNl=Nl-N0，若ΔNl>0，重复步骤一，此时令样本数量为ΔNl重新计算Ql，Ql-1；

步骤六：依据式(10)进行收敛性检查，确定最高层级L，若不满足式(10)条件，令L=L+1重回步骤二。

图4 Cl和Ql随层级的变化

3.3 结果分析

1)计算效率对比

本节从计算时长和采样数量两方面说明MLMC方法在运载火箭结构动力学不确定性分析的高效性。图 5比较了MC方法和MLMC方法在达到指定相对均方误差θ时的实际仿真时间，结果显示，在不同θ下，MLMC方法计算的时长始终小于MC方法，计算效率提高了70～80倍。

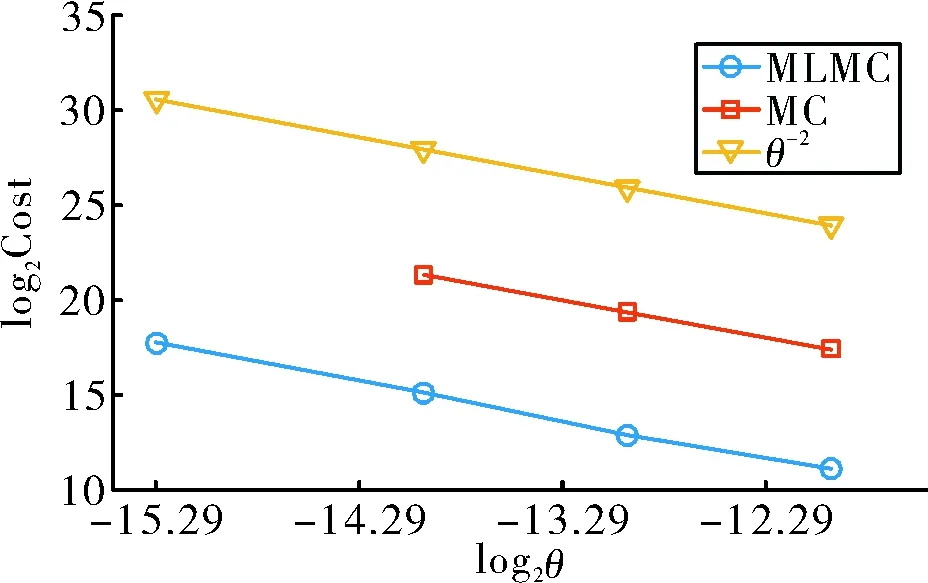
图5 计算时长对比

表2列出了在不同θ下MLMC方法和MC方法的采样数量，以及MLMC方法在L层模型上的当量采样数量，分析结果可知随着模型层级的增加，采样数量Nl大幅度下降；当精度要求提高时，每层的采样数量接近于等幅度增加，这是由式(8)决定的；虽然MLMC方法在各层级模型上的总采样数量总体高于MC方法，但是其绝大部分的采样点集中在计算代价非常小的0层模型上，这解释了图 5显示的MLMC方法计算时长较MC方法大幅度降低现象，对于MC方法，上述结果在θ=2.5×10-5时的值省去了，这是由于其计算代价巨大，难以接受。

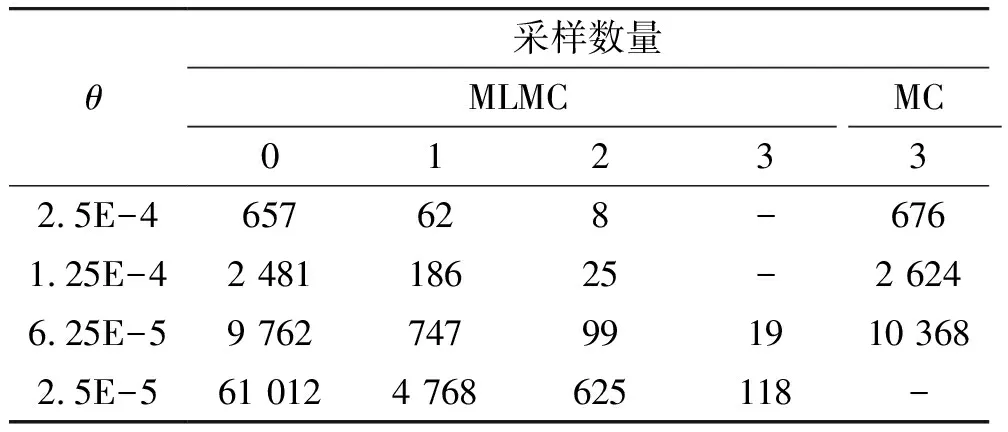
表2 MLMC和MC方法采样数量对比

2)计算结果分析

图 6给出了MC方法Ql的方差和θ=6.25×10-5时MLMC方法Yl的方差情况，随着层级的增加，Yl的方差大幅度下降，说明MLMC方法能明显减小方差，参数β可由Yl方差图线斜率估计得到，Ql的方差大致保持常数。因此，MLMC方法的L层模型响应的方差特性可以由低层模型表示，而其均值特性可以通过MLMC方法给出的式(4)进行逼近，应用这个思想，该算例中的中捆绑直杆动响应极值的均值为4.108×104N，方差为1.74×104N2。

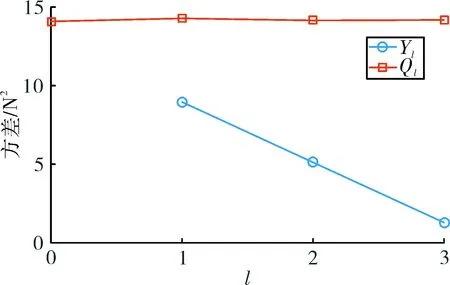
图6 方差与层数之间的关系

3)参数估计

表 3列出了MLMC采样的参数估计结果，在这四种情况下均β>γ，按定理1的结论，MLMC在本算例中的计算代价应正比于θ-2，这符合图 5所给出的结果。

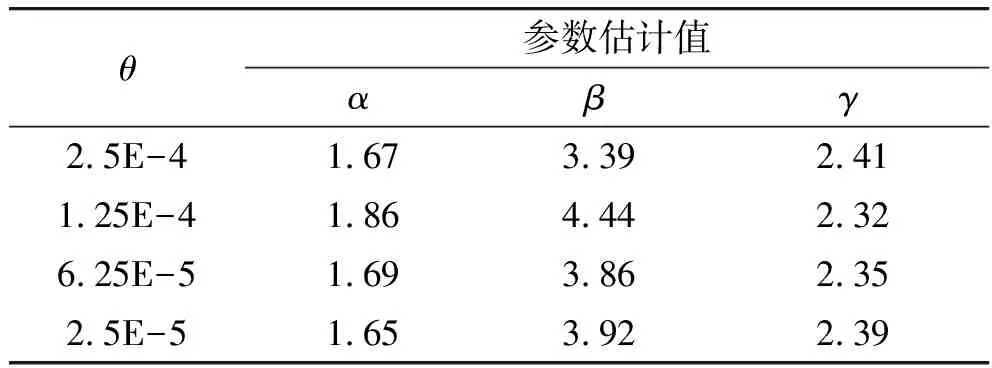
表3 MLMC方法参数估计

4 结论

文中将MLMC方法引入到运载火箭结构动力学不确定性分析中。考虑模型的不确定性，分析了发动机点火工况下运载火箭捆绑连杆响应。结果表明，相较于MC方法，MLMC方法的计算效率有很大的提高，在文中给出的计算精度下，计算效率提高了70～80倍；同时，MLMC方法通过低层模型模拟不确定性传播的方差特性，通过低高层模型的结合逼近不确定性传播的期望特性，能高效地获取包含均值和方差的捆绑连杆响应极值统计特性，为运载火箭初步设计阶段考虑不确定性的强度分析和结构设计提供基础。