数字滤波对扰动基座初始对准影响分析*
2019-11-13梅春波
阮 娟,梅春波,谭 磊
(西安现代控制技术研究所, 西安 710065)
0 引言
捷联惯导初始对准按对准过程可以分为粗对准和精对准[1-2]。粗对准为后续精对准过程提供粗略的姿态初始值。针对基座存在大幅晃动干扰的情况,文献[3]提出了一种巧妙的惯性系粗对准算法。该算法能够隔离基座的晃动对粗对准过程的影响,解决了大幅角运动情况下的粗对准问题。
在实际的大幅度角运动对准环境中,惯导系统除了会受到角运动干扰外,还会受到线运动的干扰,如发动机的振动、阵风等干扰。为了降低各种线运动干扰对初始对准的影响,各种数据预处理算法被应用到初始对准中,如FIR数字滤波算法[4]、最小二乘滤波[5]、多尺度小波滤波算法[6]、提升框架小波滤波[7]及IIR低通滤波算法[8]等。
文中在上述工作的基础上,基于抗扰动初始对准原理,采用FIR数字低通滤波器来做数据预处理,然后利用惯性系粗对准算法完成晃动基座下的粗对准过程,利用Kalman滤波算法实现精对准。其次,利用实验室惯导系统模拟扰动环境,设计验证试验,验证所设计算法的有效性。最后,给出验证结果及相关结论。
1 抗扰动初始对准算法设计
抗扰动初始对准算法由三部分组成:第一部分是处理对准过程中的角晃动干扰,通过引入惯性系,进行姿态阵分解和姿态跟踪算法解决;第二部分是处理对准过程中的线加速度干扰,通过引入线性FIR滤波预处理算法解决;第三部分是在惯性系内设计的卡尔曼滤波精对准算法,完成精对准。
1.1 角晃动干扰隔离原理
对姿态阵进行链式分解,即
(1)
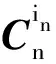
(2)

1.2 线加速度干扰的预处理
在前文定义的惯性系内,依据牛顿第二定律,可以得到惯性系比力方程为
(3)
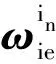
晃动基座条件下,式(3)等号右端前两项分别为基座晃动所产生的干扰加速度和干扰哥氏加速度。虽然存在干扰速度,但是基座的平均位置并未改变,因此,干扰加速度和干扰速度均可视为高频小幅值周期函数。将式(3)等号右端前两项合称为干扰加速度,记为ar(t),则有
fin(t)=-gin(t)+ar(t)
(4)
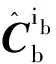
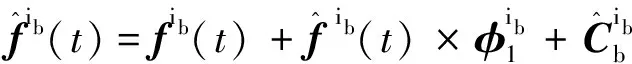
(5)
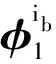
将式(4)代入式(5)中,则有
(6)
等式右端第一项为重力加速度和加速度计测量误差之和,二者在频域内有重叠,不可分离,为低频分量;第二项为周期性干扰加速度项,为高频分量。
针对式(6),可以在频域内设计数字低通滤波算法,抑制其中的干扰加速度。不同的应用背景,干扰加速度的频率范围不同,所使用的低通滤波手段也有所差别。
文中设计具有线性相位的FIR数字低通滤波器来对干扰加速度进行处理,滤波器系数满足:h(n)=h(N-1-n),即h(n)为偶对称,N取为奇数。该滤波器具有线性相位,通带内的数据经过该滤波器后,仅仅是在时间上有延迟,幅度和形状保持不变,延迟量为(N-1)/2拍,延迟拍数乘以采样周期即是对应的延迟时间。
设计低通滤波器时,需要了解实际对准环境中基座扰动的频率范围,主要指线运动的频率范围。文献[9]通过对实际的车载环境下数据的分析得出,车载条件下,由于受到发动机振动影响或人为干扰而导致的扰动加速度的频率均在0.5 Hz以上。文献[3]则指出舰载环境中扰动加速度的频率均在1/15 Hz以上。在实际应用中,以此为选择标准,就可以完成对低通滤波器的设计。
(7)
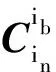
(8)

1.3 惯性系卡尔曼滤波精对准
在惯性系精对准过程中,利用陀螺仪输出进行载体系姿态跟踪,考虑器件误差,则有
(9)
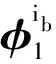
考虑器件误差时,载体系比力积分模型为
(10)
由此,可建立惯性系线性卡尔曼滤波精对准方程如下:
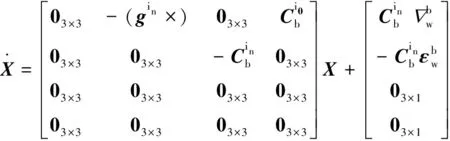
(11)
2 试验验证
2.1 验证方案设计
数据采集时序图如图1所示。
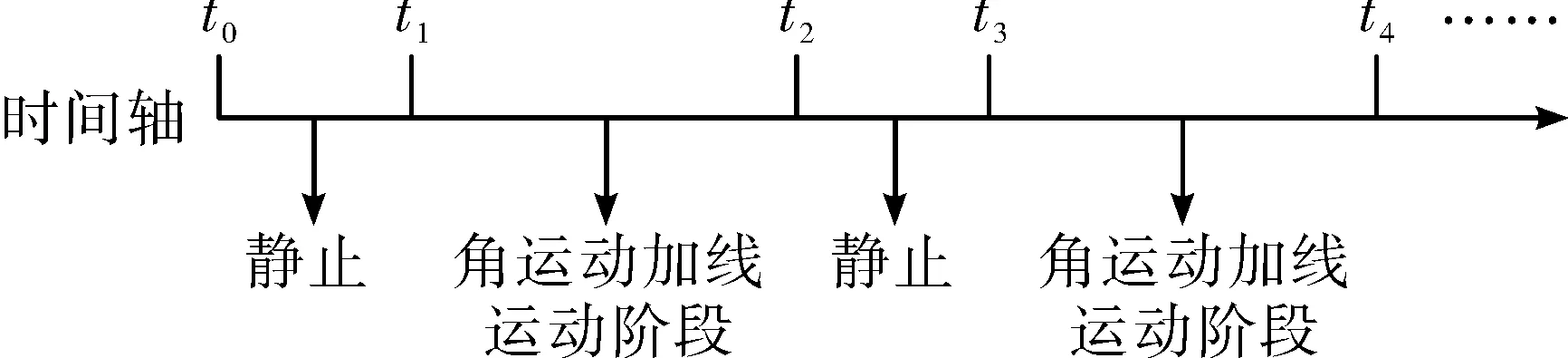
图1 验证试验时序图
在图1中,利用静止阶段数据完成捷联惯导系统的静基座初始对准,获取t1时刻的姿态初值。从t1时刻开始进行捷联姿态更新,以捷联姿态更新的结果作为实时的姿态真值。然后,利用t1至t2时间段内的数据完成基于重力信息的初始对准,并用参考姿态来评估对准的效果。
验证试验在实验室内进行,试验采用的惯导设备为激光捷联惯导系统。陀螺漂移重复性误差为0.008°/h,加速度计零位稳定性≤4.0×10-5g,数据更新周期为10 ms。验证试验共进行了3组,两组在试验车上进行,车上第一组施加小幅度的角晃动和线运动干扰;车上第二组施加了稍大幅度的角晃动和线运动干扰;第三组利用人力操作惯导系统模拟恶劣的大幅角晃动干扰和线运动干扰。
2.2 试验结果
第一组微幅晃动试验结果如图2~图5所示。
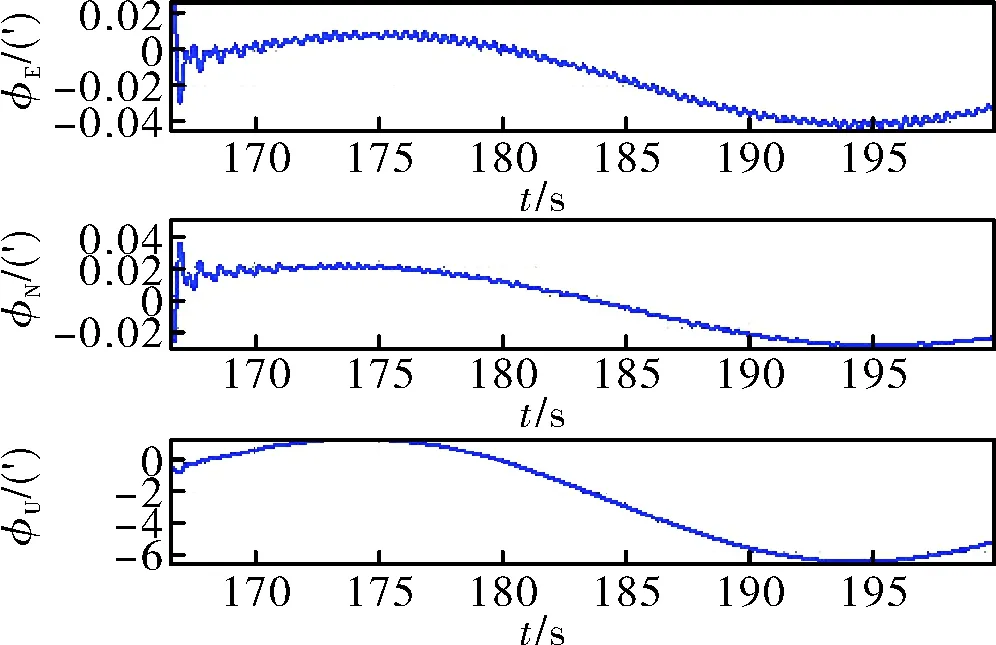
图2 经过数字滤波预处理后粗对准误差
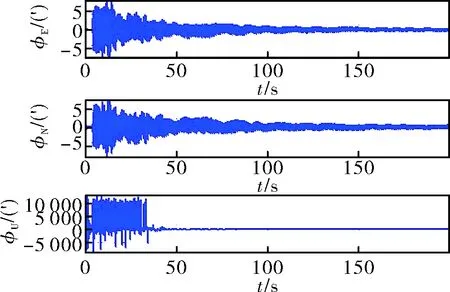
图3 未经数据预处理粗对准误差

图4 经过数字滤波预处理后精对准误差
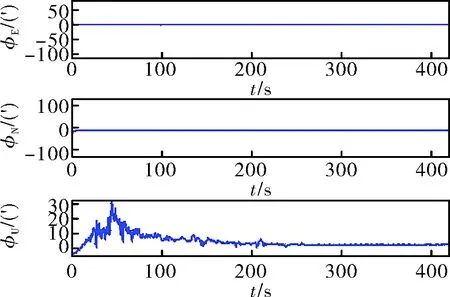
图5 未经数据预处理精对准误差
第二组晃动试验结果如图6~图9所示。
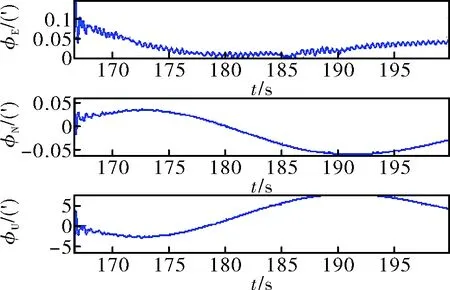
图6 经过数字滤波预处理后粗对准误差
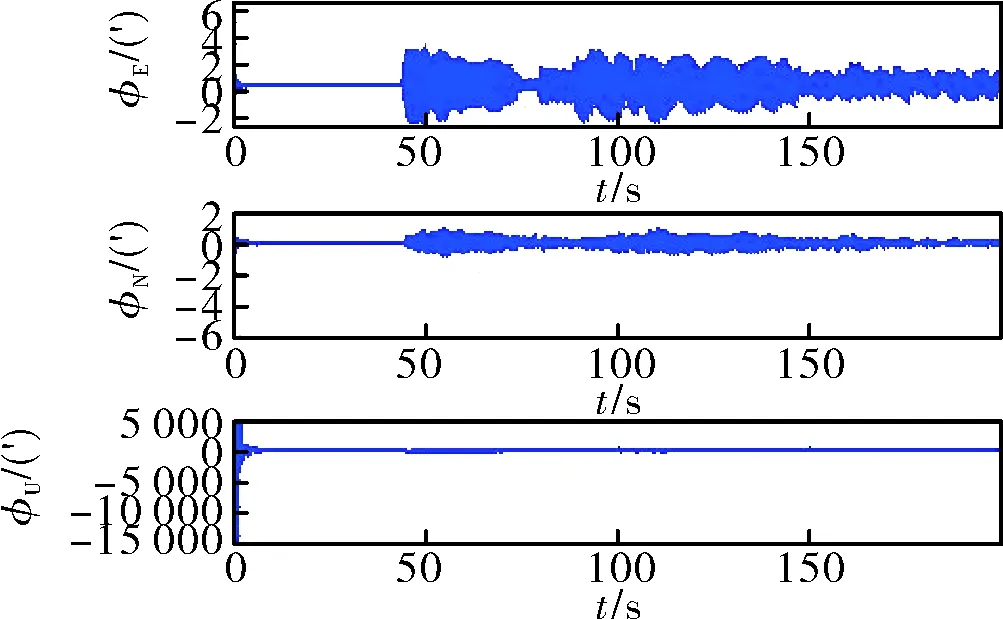
图7 未经数据预处理粗对准误差
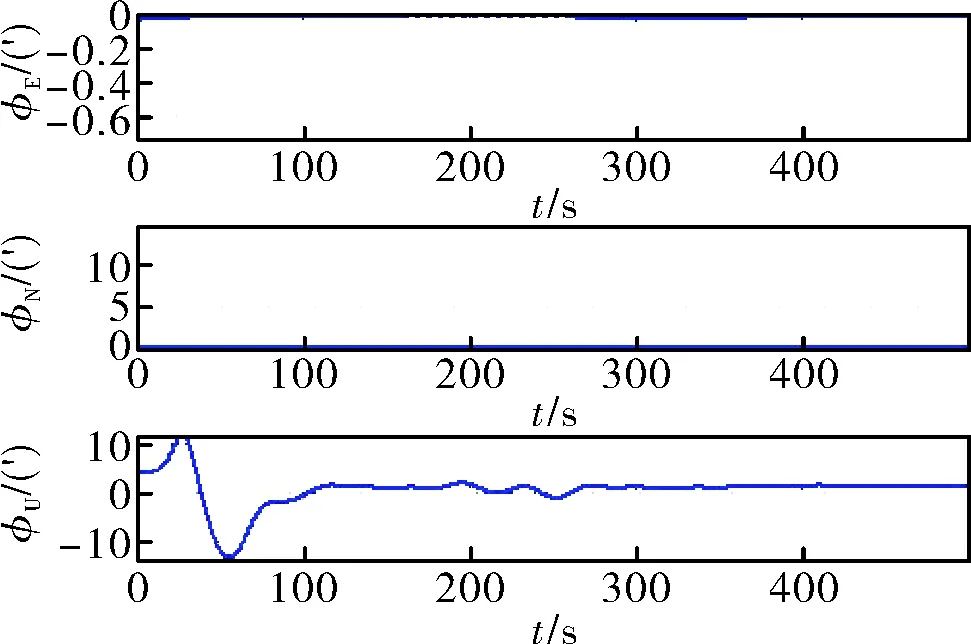
图8 经过数字滤波预处理后精对准误差
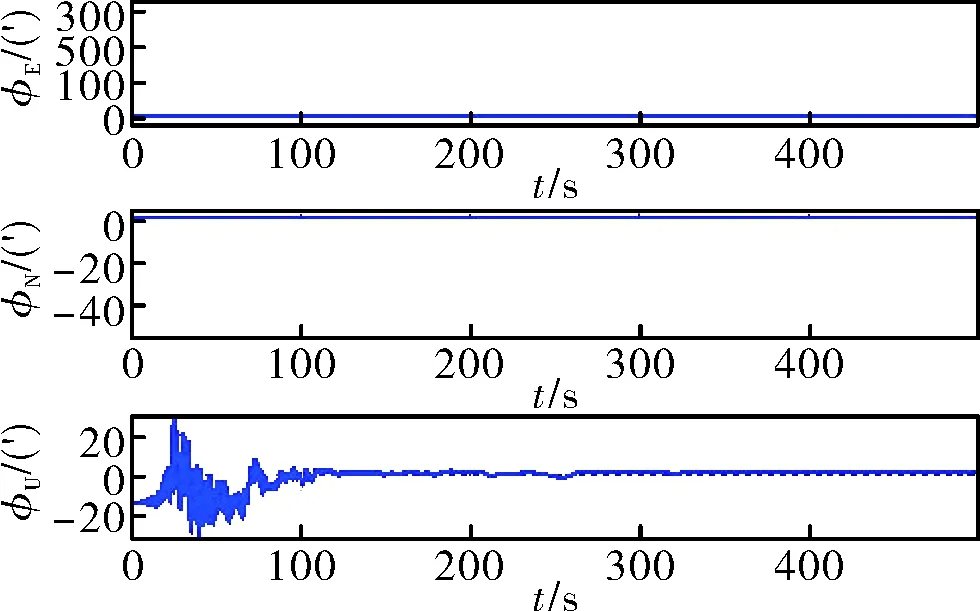
图9 未经数据预处理精对准误差
第三组恶劣晃动试验结果如图10~图14所示。
其中,φU、φN、φE分别为天、北、东方向的对准姿态误差,φ、γ、θ分别为航向角、滚转角和俯仰角。
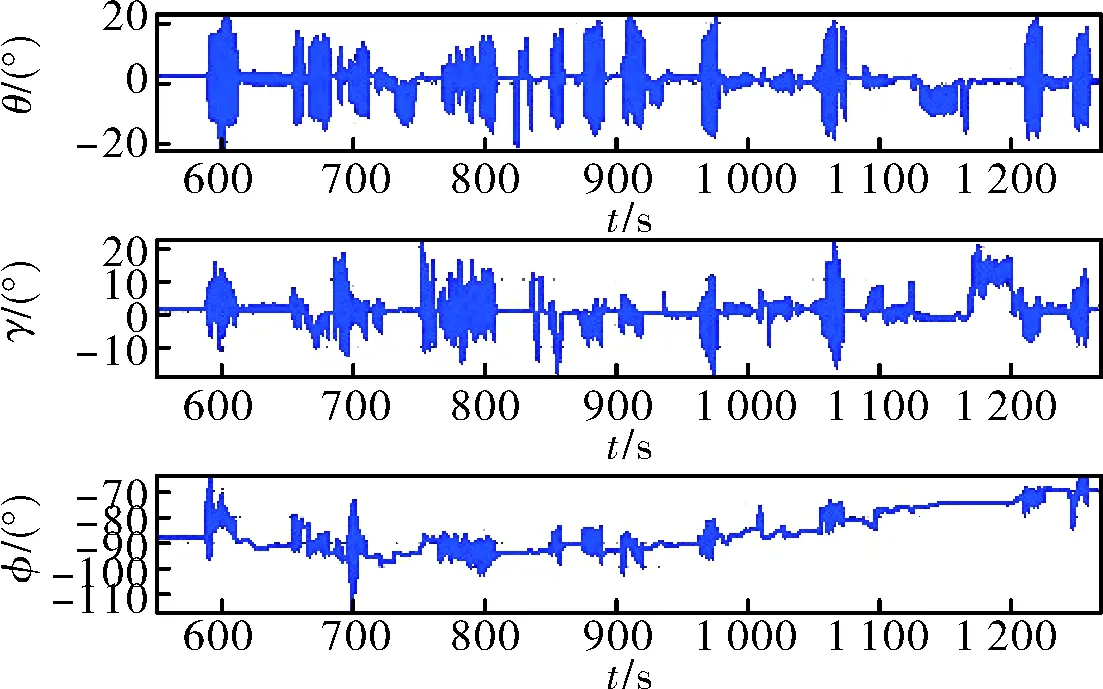
图10 第三组恶劣晃动条件下的惯组姿态变化
2.3 试验结论
根据3组验证试验,可以得到如下结论:
1)FIR数字滤波器能有效地抑制噪声及未知线运动干扰,提高粗对准的收敛速度和收敛精度。
2)FIR数字滤波器对精对准的结果影响较小,经过滤波处理后精对准的结果更加平滑,但是精对准的精度基本保持不变。
3)3种试验条件下,所设计的初始对准算法均可在5 min内达到与静基座初始对准相同的精度。

图11 经过数字滤波预处理后粗对准误差
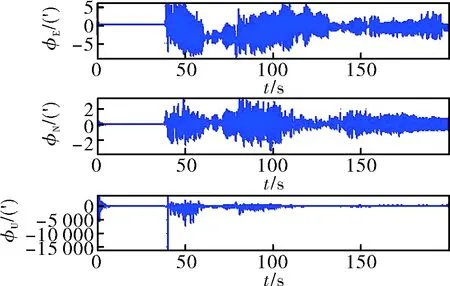
图12 未经数据预处理粗对准误差
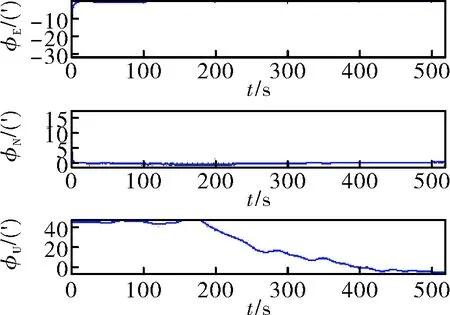
图13 经过数字滤波预处理后精对准误差

图14 未经数据预处理精对准误差
3 结论
通过文中的分析和试验验证结果,可以发现,通过引入低通数字滤波对惯导数据进行预处理,可以实现对粗对准过程中载体线运动干扰的抑制,从而改善惯性系粗对准算法的收敛效果和收敛速度,同时对精对准的估计结果有一定的平滑作用。
