制导与发射分离的协同防空杀伤区模型与仿真*
2019-11-13贺正洪吴舒然
伍 凯,贺正洪,吴舒然
(空军工程大学研究生院, 西安 710051)
0 引言
随着网络信息技术的飞速发展,武器装备的更新换代,空袭样式在不断发生变化,平台化防空作战体系也逐渐在向网络化防空体系过渡[1]。在传统平台中心化体系下,由于单个雷达的探测能力有限,雷达之间信息不能共享实现接力制导,发射平台与制导平台不能实现分离,而在网络化防空体系结构下,通过协同制导方式,雷达的制导能力大大提升,发射平台的作战范围不再受限于单个雷达的制导能力,可将发射平台与制导平台分离部署,使导弹的有效射程得到最大化发挥,因此,对于制导与发射相分离的防空导弹杀伤区的研究是必要的。目前建立的协同杀伤区模型大部分是基于舰舰协同制导,发射平台与制导平台是一体化部署。文献[2]给出了杀伤区远界的粗略计算方法;文献[3]基于三维比例导引模型建立了舰空导弹协同制导杀伤区远界模型,但缺乏考虑导弹的射程因素;文献[4]对舰舰协同制导情况下研究了防空导弹水平杀伤区模型,但考虑的边界模型不够充分。在此基础上,文中建立了发射平台与制导平台相分离的杀伤区模型。
1 复杂环境下导弹制导能力分析
当电磁波在自由空间传播时,由雷达原理可知探测距离为[5]:
(1)
现代防空作战中,由于低空目标、干扰目标、隐身目标极大地限制了雷达的能力,导致防空导弹不能最大化发挥其作战性能[6],下面对复杂环境下雷达的探测制导能力进行分析。
1.1 低空目标
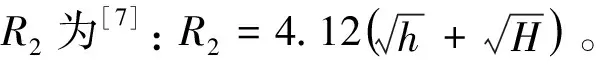
考虑地形地物是电磁波的屏障,其背后雷达不能发现目标,则地物造成的遮蔽角ε对雷达探测距离的影响[7]
(2)
式中:RD为考虑电波折射后的地球等效半径。
1.2 干扰目标
电子干扰能够有效减小雷达的探测距离及探测精度,有源压制干扰主要包括远距离支援干扰、随队干扰和自卫干扰。
远距离干扰一般情况下干扰机作用距离远,干扰源位于防区外,干扰功率较大,此时雷达的最远距离模型为[8]:
(3)
式中:Kj为压制系数,即目标功率信号的干信比;Bj为干扰机频带宽度;Br为雷达频带宽度;yj为干扰信号的极化损失。
随队干扰不仅能影响雷达的探测距离,而且能造成雷达的测角干扰。自卫干扰与随队干扰的雷达探测距离模型一致[9],均为:
(4)
1.3 隐身目标

则在复杂空情下,雷达最远探测距离
Rmax=min{R1,R2,R3,R4,R5,R6}
(5)

2 协同制导交接分析
制导交接[10]是协同制导技术中的一个重要组成部分,它将防空导弹的制导权由跟踪制导网的一个制导节点转移到另一个制导节点。制导的交接方式一般分为两类[11-12]:直接交接和间接交接。
直接交接指的是接班平台B利用交班平台A的导弹实时测量数据进行的交接班,这就要求两个制导平台具有足够距离的重叠工作空域,即交叠区纵深ΔRz满足:ΔRz≥Vfth,式中:Vf为防空导弹飞行速度,th为完成制导交接所需时间。见图1。
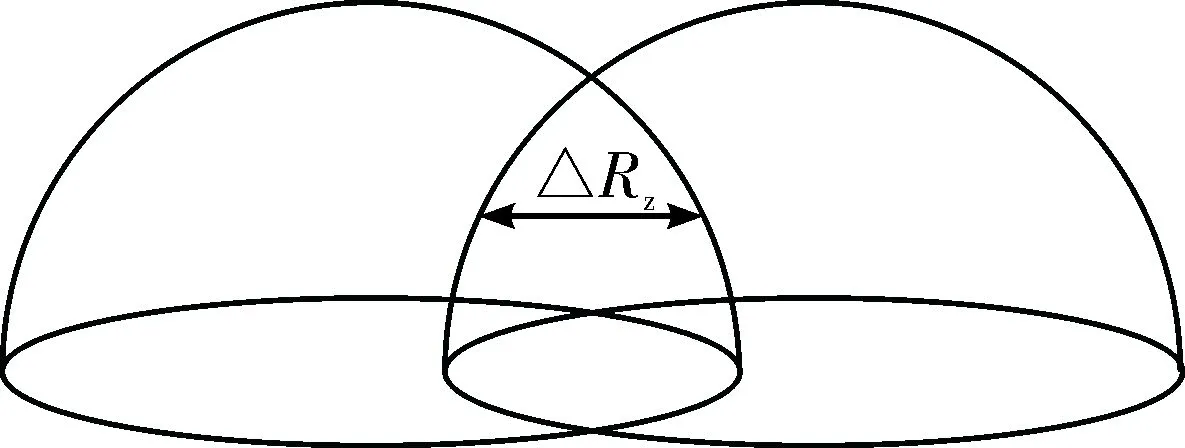
图1 直接交接制导示意图
间接交接指的是接班平台B利用交班平台A对导弹的实时外推位置指示信息进行跟踪制导,当制导空域没有交叠时必须采用间接方式制导交接。由于导弹自毁时间td的限制,制导平台的间距ΔRj满足:ΔRj≤Vf(td-th)。见图2。
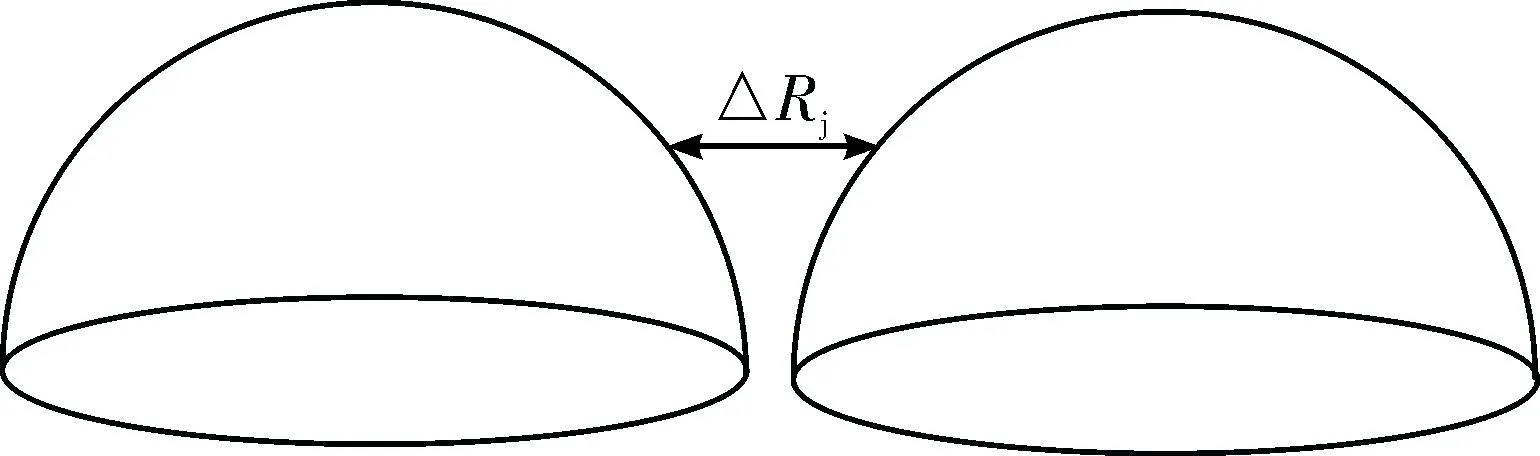
图2 间接交接制导示意图
如果两制导平台相对位置过远,不满足直接交接和间接交接距离要求,则不能进行制导交接。
3 发射与制导相分离的杀伤区边界模型
为了建立制导与发射分离的防空导弹杀伤区模型,需对战场态势进行必要的假定。假设目标做水平、匀速直线运动且不作机动;假设防空导弹指向弹目遭遇点以平均速度做匀速直线运动,导弹与目标速度比为k;假设在网络化条件下,武器系统可提前获知空情预警信息,不必考虑武器系统反应时间,即目标在制导范围边界时发射平台立刻发射导弹。
3.1 交班平台水平杀伤区模型
以发射平台O为圆心,目标来袭平行方向为X轴,建立如图3所示的杀伤区模型,横坐标X表示目标的水平距离,纵坐标Y由目标航路捷径p决定。目标在飞至跟踪制导雷达A最大威力范围C点时,发射平台O发射导弹,与目标在最远拦截点D相遇。发射平台O与制导平台A距离为L;两平台连线与X轴的夹角为α;制导平台A的跟踪制导半径为RA;发射平台O发射导弹最远射程为R,由导弹最大飞行距离与引信决定。
杀伤区边界分析:射线OS和OK分别为杀伤区的左右侧界[5],由导弹的可用过载和引信与战斗部配合效率决定其对应的参数最大航路角qmax;SK为杀伤区的近界,由导弹的引入段距离dsj确定;远界HG受到4个约束,即射线OS、OK的侧边界约束,制导平台A的制导半径RA约束,发射平台O导弹最远射程R约束,导弹与目标相遇点的连线边界约束。
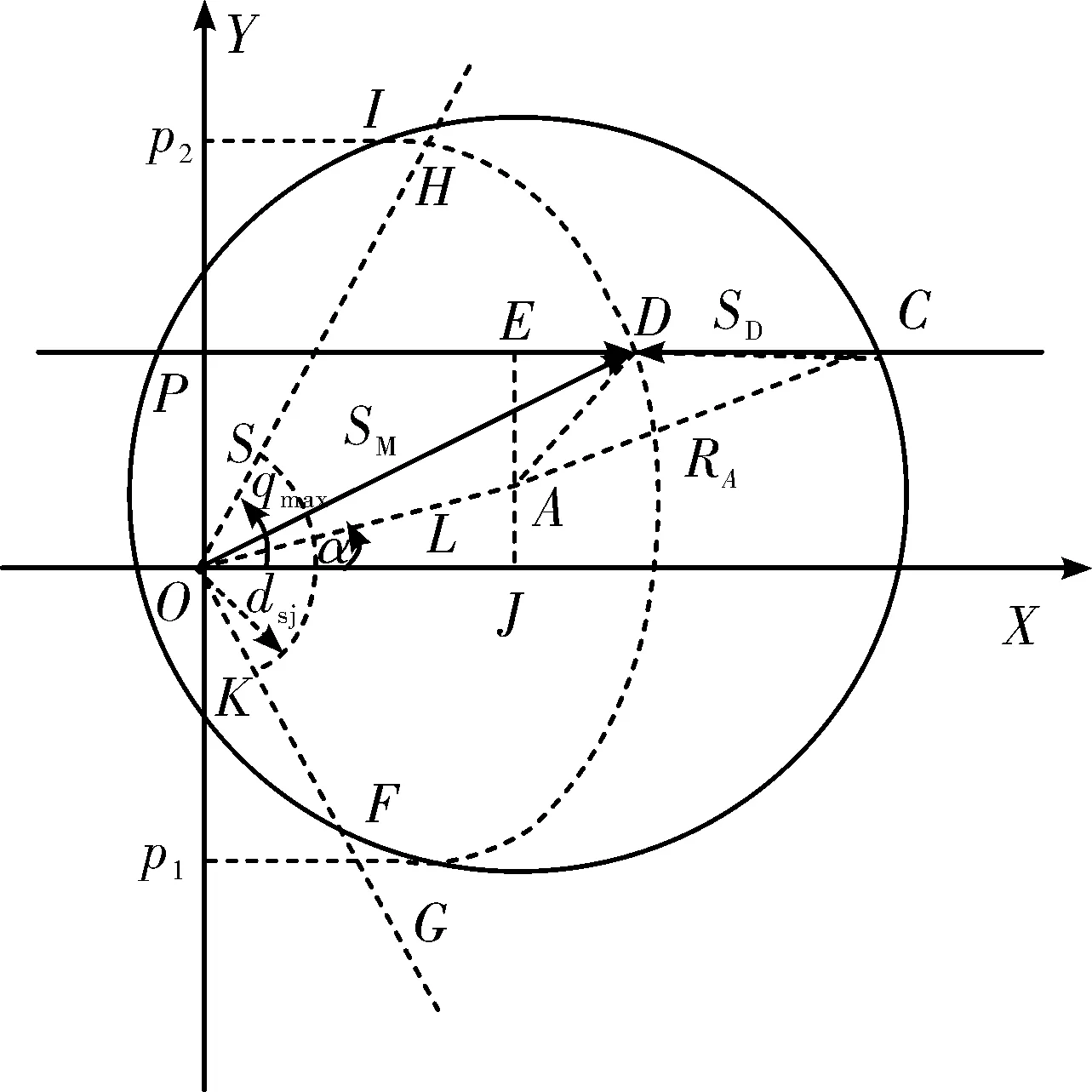
图3 交班平台水平杀伤区模型
下面讨论导弹与目标相遇点的连线边界,易知点A的坐标为(Lcosα,Lsinα),设点D的坐标为(x,p)。由几何关系可得:
(6)
由此可解得遭遇点的连线方程为:
(7)
联立制导平台A的探测范围方程:
(8)
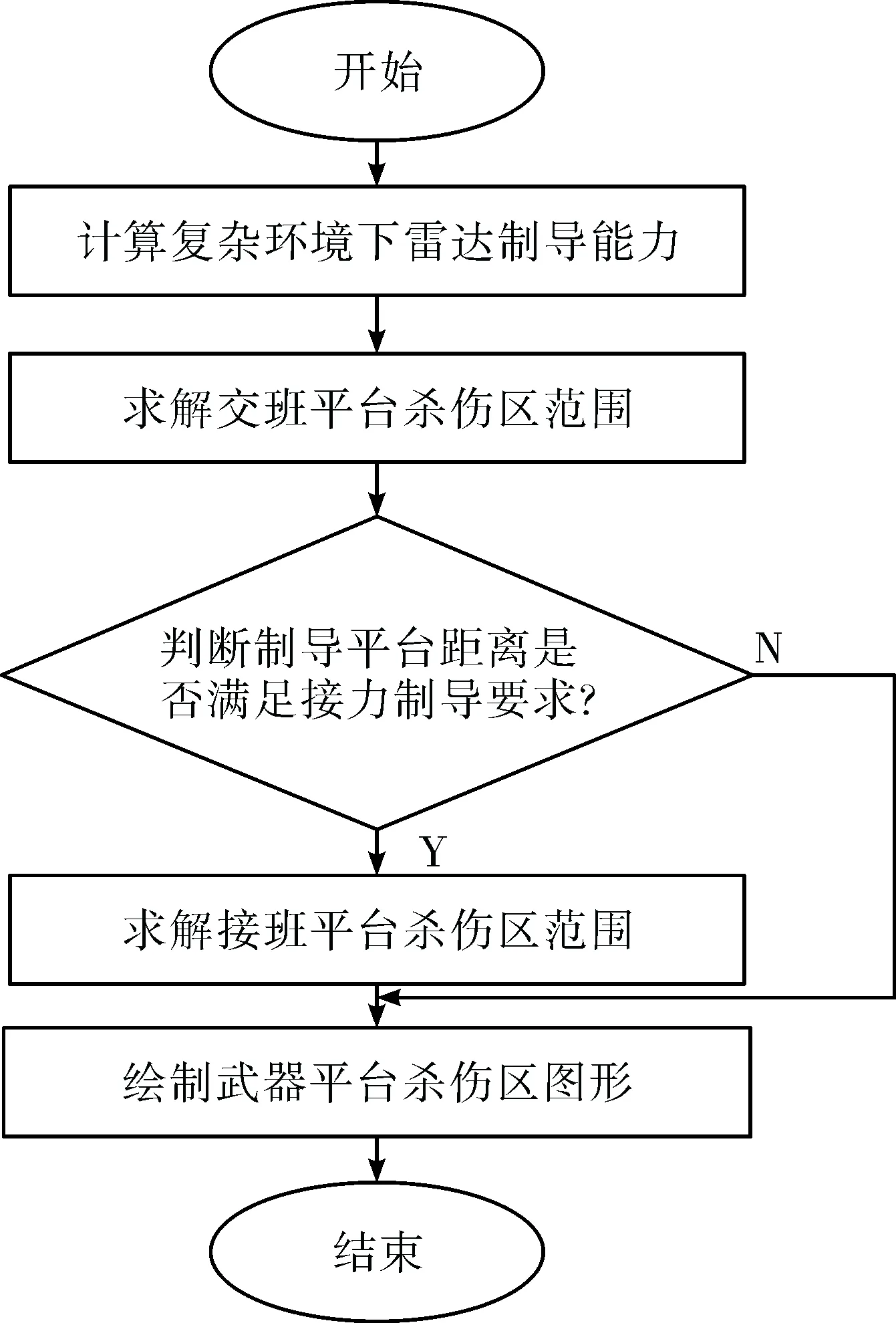
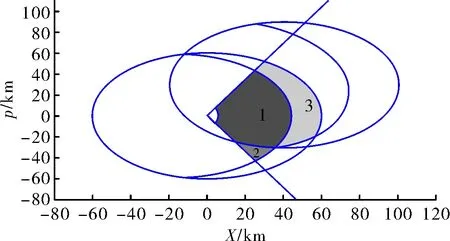
由图3分析可知航路捷径边界点取值必位于制导平台左侧,即满足:x 由此,化简可得航路捷径取值满足以下方程组: (9) 设方程的解为(x1,p1)和 (x2,p2)。可得航路捷径p的取值范围:p1≤p≤p2。联立式(9)和p的取值范围可以准确描述导弹与目标相遇点的连线。 在单个制导平台进行制导情况下,由于制导能力有限,导弹与目标相遇点的连线构成的边界是杀伤区远界的主要约束,故交班平台A的杀伤区基本形状如图3所示区域DHSKFG,杀伤区范围可由式(10)描述: (10) 以发射平台O为圆心,目标来袭平行方向为X轴,建立如图4所示的协同杀伤区模型,发射平台O与接班平台B距离为L,两平台连线与X轴的夹角为α;交班平台A的跟踪制导半径为RA,接班平台B的跟踪制导半径为RB,间距为d,满足接力制导要求;目标在飞至接班平台B最大威力范围C点时,发射平台O发射导弹,经交班平台A进行初始制导后与接班平台B进行制导交接,目标与导弹在最远拦截点D相遇。 图4 接班平台水平杀伤区模型 杀伤区边界分析:由于接班平台B与发射平台O距离较远,杀伤区近界基本不受导弹引入距离dsj限制,主要考虑接班平台B的制导距离限制条件;接班平台B的遭遇点连线方程与交班平台A的计算方法相同;杀伤区的左右侧界仍由最大航路角qmax决定;杀伤区远界不仅受到导弹与目标相遇点的连线边界约束,而且要考虑发射平台O导弹最远射程R约束。 故接班平台B的杀伤区基本形状如图4所示区域DEFGHI, 杀伤区范围可由式(11)描述: (11) 根据上述数学模型和计算原理,制导与发射平台相分离的协同制导水平杀伤区模型的绘制流程如图5所示。 图5 制导与发射分离的协同杀伤区绘制流程图 参数设定:假设发射平台O最大射程R=100 km;交班平台A和接班平台B在复杂环境下的跟踪制导半径RA=RB=60 km;导弹与目标速度比k=3; 导弹的引入距离dsj=5 km;最大航路角qmax=60°;交班平台A与发射平台O距离L=50 km,夹角α=37°;接班平台B与交班平台A距离d=30 km,位于同一水平线上,满足接力制导条件约束。 平台化和制导与发射分离的水平杀伤区仿真如图6所示,区域1、2为制导与发射一体化的水平杀伤区区域,区域1、3为制导与发射分离的水平杀伤区区域。由仿真实例可知:通过制导与发射分离的防空部署,可增加主要防御方向的拦截纵深,扩大了杀伤区范围,但在次要方向会造成一定的杀伤区损失,这就要求在防空部署时根据敌情合理部署两平台的相对位置,使保卫区域尽可能地位于1、3区域。 图6 平台化和制导与发射分离的水平杀伤区 制导与发射分离的协同水平杀伤区仿真如图7所示,区域4、5为交班平台A的水平杀伤区区域,区域5、6为接班平台B的水平杀伤区区域。由仿真可知:通过接力制导,可将杀伤区范围进行扩张,最大程度地发挥导弹的最大射程,但要注意交接班平台位置,保证满足接力交接条件。 图7 制导与发射分离的协同水平杀伤区 文中通过改变航路捷径结合数学逻辑推理得出弹目遭遇点边界,分析了协同制导交接条件及杀伤区边界影响因素,建立了协同水平杀伤区模型。仿真分析表明,制导与发射分离部署能有效增加重要方向拦截范围,接力制导能够有效发挥防空导弹的最大射程。由于影响杀伤区边界的因素极为复杂,当假设条件改变时,还需根据情况进行改进模型。3.2 接班平台水平杀伤区模型
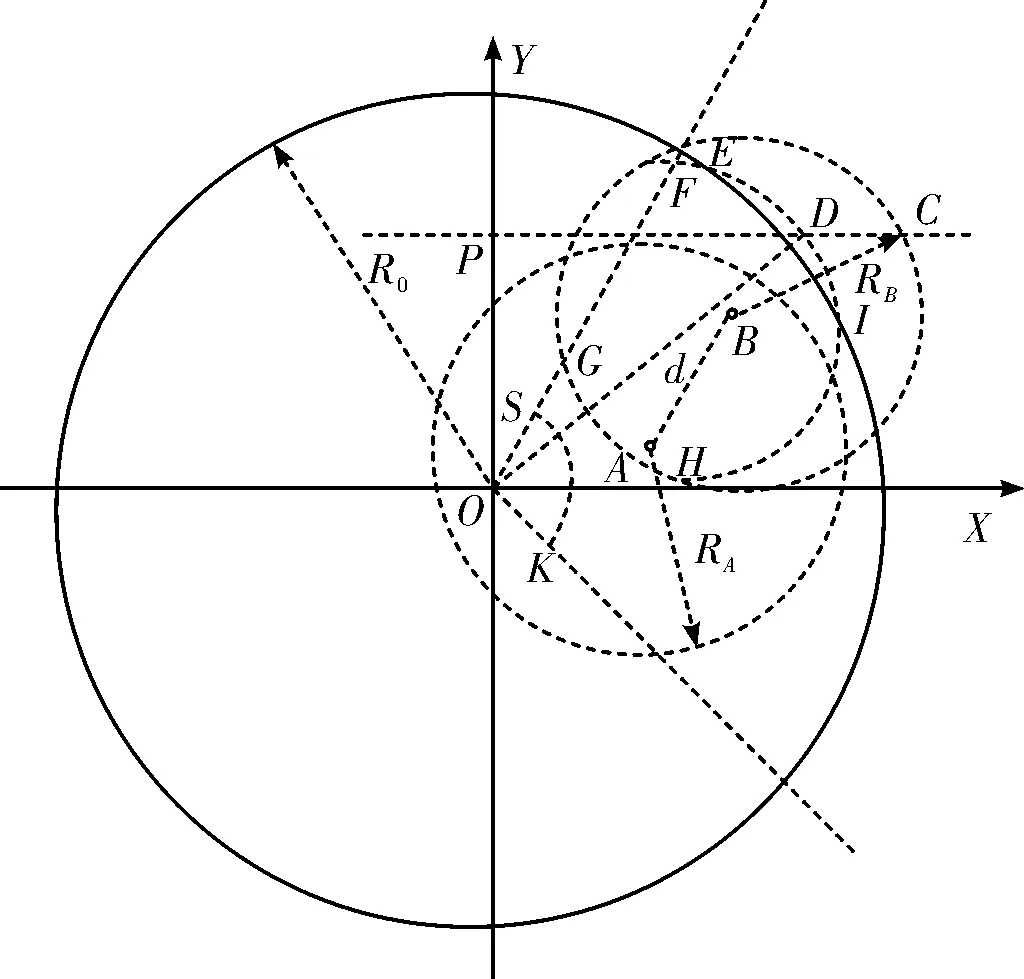
3.3 发射平台综合杀伤区确定
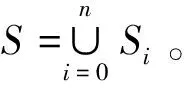
4 仿真校验

5 结束语
