目标做规避机动条件下的三维空空导弹攻击区建模与仿真*

2019-11-13史振庆梁晓龙张佳强任宝祥

弹箭与制导学报 2019年3期

史振庆，梁晓龙，张佳强，刘流，任宝祥

(空军工程大学空管领航学院，西安 710051)

0 引言

空空导弹攻击区对空战态势的评估判断有着重要的作用，能够为我方的作战决策提供关键依据[1]，同时也是空空导弹的重要性能之一[2]。研究目标做规避机动条件下的空空导弹攻击区，更加符合真实的作战需求，对空战具有更高的参考价值。

在提高攻击区的计算速度和精度上，学者们做了大量的工作，并取得了丰硕的成果。文献[3]结合变步长积分，气动系数拟合及最大最小边界快速搜索法，建立弹道模型，得出了一种攻击区的快速求解方法。文献[1]采用曲线拟合的方法获得攻击区的距离函数，得到了较好的结果。文献[4-7]利用神经网络的方法来求解导弹的攻击区，极大地提高了攻击区求解的速度。文献[8]在攻击区求解的基础上，基于攻击区和杀伤概率对空战态势进行评估。文献[9-12]对攻击区的建模与仿真进行了相关研究，得出了可行的求解方法。国外计算攻击区更多地采用快速模拟方法[13-14]，通过解算简化的导弹与目标运动模型来提高攻击区计算速度，以满足机载实时火控解算的要求。上述研究更多的是在二维攻击区中，且目标运动类型较为简单，攻击区求解精度较低[15]。如何准确地对目标做规避机动条件下的三维攻击区进行计算，成为当前必须面对而又亟须解决的问题。

针对上述问题，文中利用三维纯比例导引律，建立了目标受到导弹威胁而做规避机动条件下的三维攻击区的数学模型，并对目标做不同的规避机动时的三维攻击区进行了仿真分析。

1 数学模型

1.1 空空导弹运动模型

在惯性坐标系下，导弹的运动学方程为：

(1)

式中：xm、ym、zm分别为导弹在惯性坐标系下x、y、z三个方向上的坐标；vm、θm、φm分别为导弹的速度、弹道倾角和弹道偏角。

在弹道坐标系下，导弹的三自由度动力学方程模型为：

(2)

模型中：Fx、Fy、Fz分别为除推力外导弹所有外力分别在弹道坐标系各轴上分量的代数和；Px、Py、Pz分别为推力P在弹道坐标系各轴上的分量。由上述动力学方程模型，得导弹的三自由度动力学方程为：

(3)

式中：Mm为导弹质量，P、X分别为导弹所受推力和空气阻力，θm为弹道倾角；nmy、nmz分别为俯仰和偏航方向上导弹的转弯控制过载。

P、Mm随时间变化的方程分别为：

(4)

(5)

阻力X的变化规律方程为：

(6)

式中：Cx为阻力系数，ρ为空气密度，S为导弹特征面积。

1.2 目标做规避机动运动模型

目标做规避机动，可以视为在特定时间内目标作变角速率的圆弧运动的叠加。其模型表示为：

(7)

(8)

式(8)中：x(i)、y(i)为目标第i个点的坐标；vx(i)、vy(i)为目标第i个点的速度；φ(i)为传输矩阵，ωi为转弯速率；T为采样时间。

1.3 导引律模型

纯比例导引律根据与视线旋转角速度的比例关系产生控制加速度[16]。在三维情况下，控制加速度表示为：

(9)

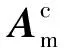
(10)

将式(10)所得俯仰和偏航方向控制加速度用于式(3)得：

(11)

2 攻击区边界搜索方法

2.1 边界搜索约束条件

空空导弹攻击时所受约束条件一般有：

1)导弹可控飞行时间约束。导弹飞行时间超过最大可控飞行时间tc时，导弹失控。

2)最小飞行速度约束。导弹飞行速度小于最小飞行速度，升力不足，飞行失控。

3)高度约束。空空导弹的飞行高度应满足大于200 m，小于20 km。

4)引信解锁时间约束。导弹和目标接近时，剩余时间小于引信解锁时间易脱靶。

2.2 黄金分割搜索方法

为了得到攻击区的边界，需要对导弹周围的目标位置进行搜索，即导弹是否能够命中该位置的目标。

以导弹为中心建立坐标系，分别对攻击区的远界和近界进行搜索。以搜索攻击区远界为例，首先确定目标相对于导弹的方位和攻击区远界的最大初始搜索范围[Rn,Rf]，计算黄金分割搜索点(弹目距离)Rg=Rn+0.618(Rf-Rn)。然后进行导弹与目标的运动仿真，通过弹道仿真限制条件和脱靶量判断导弹是否击中目标。若击中，令Rn=Rg,Rf=Rf；若未击中，令Rn=Rn,Rf=Rg，重新进行新一轮的仿真，直至满足导弹击中目标并且Rg<ε为止，此时，Rg就是所要求的攻击区远界距离。攻击区远界搜索的流程如图1所示。

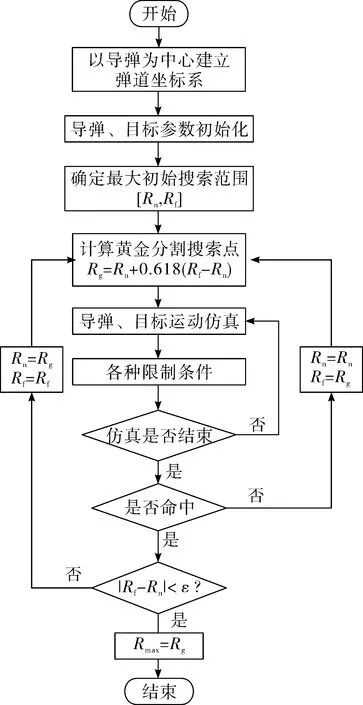
图1 攻击区远界搜索流程图

攻击区近界搜索与远界搜索方法相似，只是在迭代中若导弹击中目标，令Rn=Rn,Rf=Rg；若未击中，令Rn=Rg,Rf=Rf，其他过程与攻击区远界搜索相同。

3 仿真分析

以某型中距空空导弹为例，设弹重为200 kg，发动机工作时间为10 s，最大推力为30 kN，导弹初始速度为400 m/s，初始俯仰角、方位角均为0°，可控飞行时间为70 s，导弹升限为20 km，最低飞行高度为200 m，纯比例导引系数N=3.5。

3.1 目标做置尾机动弹道仿真分析

假设导弹初始高度为5 km，目标初始高度为5 km且保持不变，当弹目距离为20 km时，目标做置尾机动以规避导弹。图2为利用三维纯比例导引律所得的弹道仿真结果。

由图2可以看出，利用三维纯比例导引律所得的仿真结果，弹道较为平滑，导弹在实际飞行过程中较易实现。

图2 三维纯比例导引律弹道轨迹

导弹发射时刻的初始速度、初始高度是影响导弹攻击区的主要因素。为研究其对攻击区的影响规律，分别从导弹命中目标所需时间和导弹能够命中目标的最远距离，来分析导弹初始速度、高度对攻击区的影响。结果如图3、图4所示。

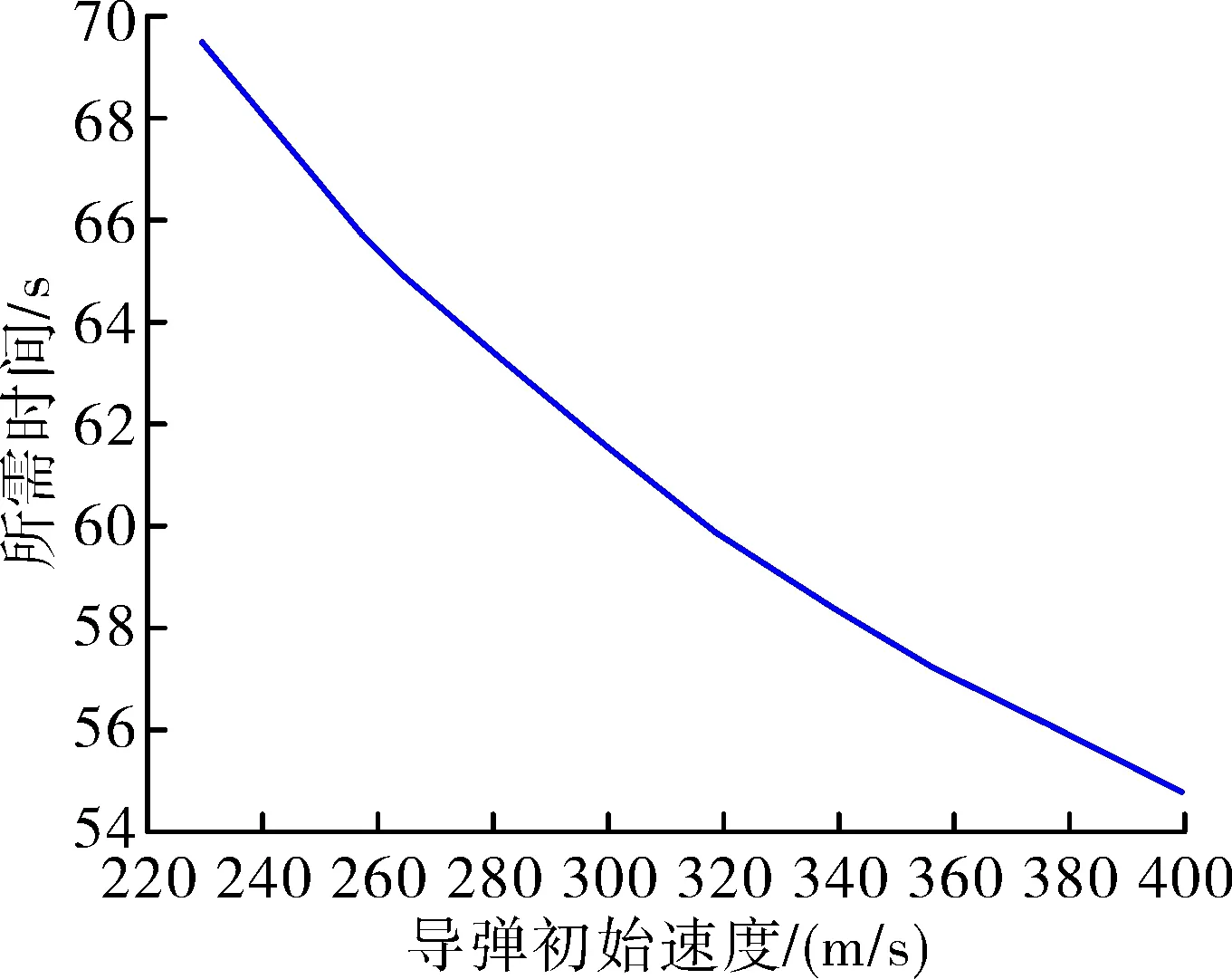
图3 所需时间随导弹初始速度变化图

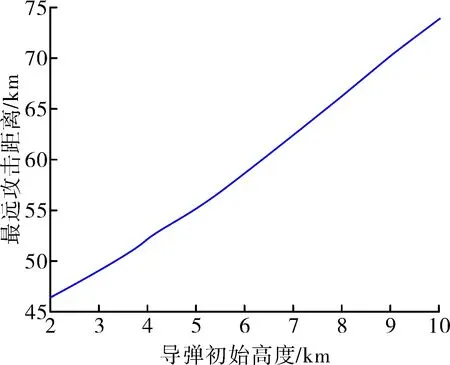
图4 最远攻击距离随导弹初始高度变化图

图3为在导弹和目标初始位置固定，导弹命中目标所需时间和导弹初始速度之间的关系。图3显示，随着导弹初始速度的增大，导弹命中目标所需时间变小。

图4为导弹最远攻击距离随导弹初始高度的变化情况。图4显示，在导弹升限范围内，随着导弹初始高度的增大，导弹最远攻击距离也随之变大。高度越低，空气密度越大，导弹在飞行过程中所受空气阻力越大，攻击区越小。因此选择合适的导弹初始速度和导弹初始高度，对增大攻击区域具有重要作用

3.2 目标做规避机动的三维攻击区仿真分析

假设导弹初始高度为10 km；目标运动初始俯仰角为0°，方位角为90°，飞行过程中高度保持不变。空战对抗中，目标在不同的弹目距离下，感知到导弹威胁而做置尾机动来规避导弹打击的攻击区进行仿真。仿真结果如图5所示，其中，x轴为载机速度方向，y轴为高度，z轴为偏航方向。

图5 弹目距离小于20 km置尾机动攻击区仿真图

图5所得攻击区的空战对抗条件为：导弹与目标开始呈迎头态势，当弹目距离小于20 km时，目标感受到导弹威胁，开始向右后做置尾机动。由图5可以发现，由于目标向右后做置尾机动，导弹右侧攻击区要大于左侧；在高度上，由于空气密度的影响，攻击区最远距离会随着高度的降低而减小。

在空战对抗时，目标做出规避机动的时机是不确定的，目标越早发现导弹威胁，就会越早做出规避机动动作。为研究目标在不同的弹目距离下做规避机动时攻击区的变化，分别对目标不同机动时机下的攻击区进行仿真。为更加清晰地比较不同的规避时机对攻击区的影响，图6展示了攻击区的仿真结果中，导弹和目标呈迎头态势时最大攻击距离的变化情况。

由图6可以发现，当目标不做机动时，在目标来向攻击区最远攻击距离为95 km，这也是攻击区的最远攻击距离；当目标在弹目距离为50 km感知到导弹而做置尾机动时，在目标来向攻击区最远攻击距离为50 km，这也是在目标做置尾机动且导弹能够命中目标的条件下，目标开始做置尾机动时的最远弹目距离，此时导弹攻击区如图7所示，其中，x轴为载机速度方向，y轴为高度，z轴为偏航方向。当目标在弹目距离大于50 km就做置尾机动时，导弹无法命中目标。

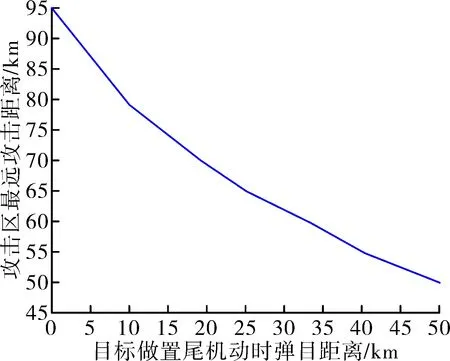
图6 攻击区最远攻击距离随目标做置尾机动时弹目距离变化图

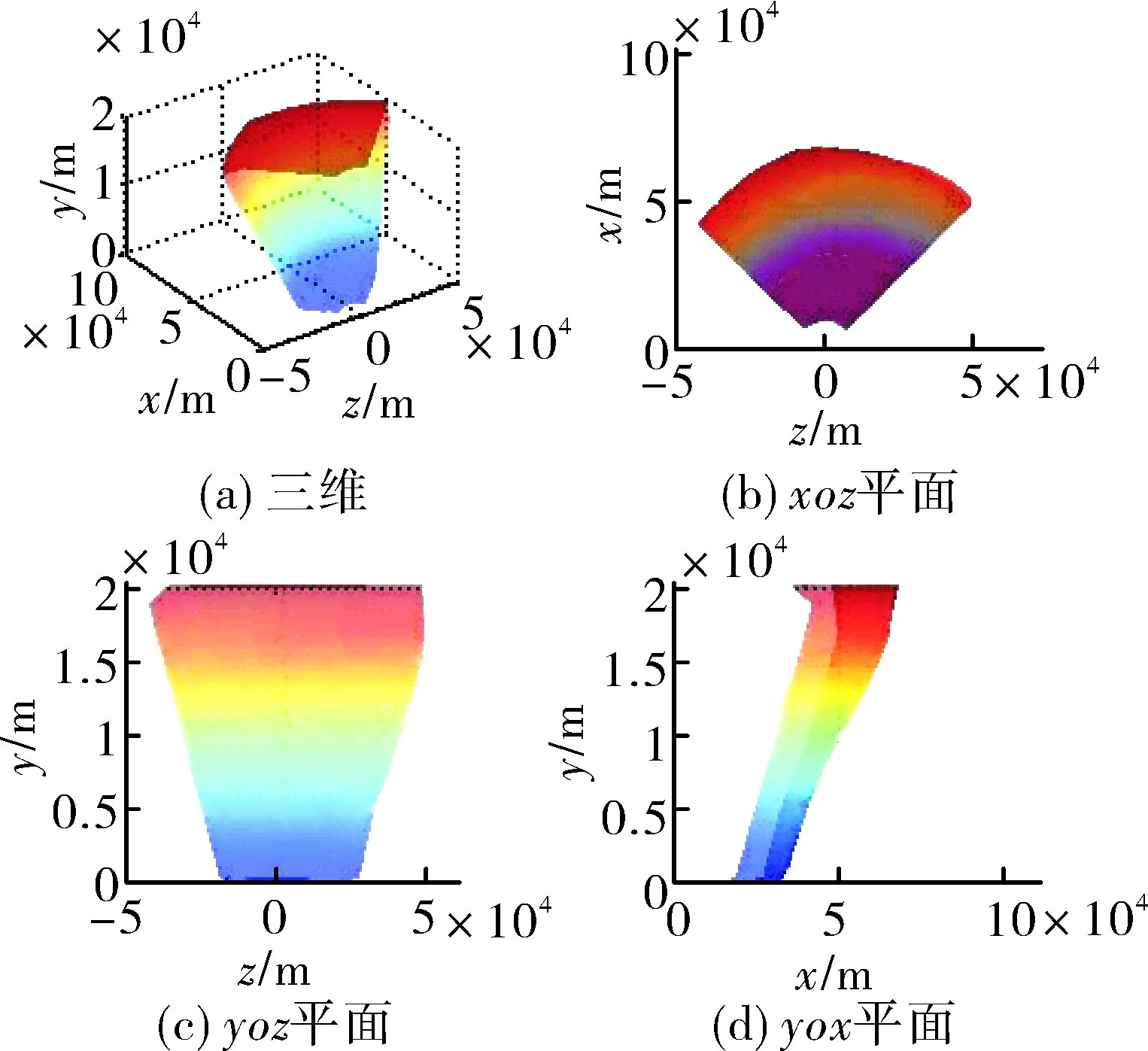
图7 弹目距离小于50 km置尾机动攻击区仿真图

以上关于目标做规避机动条件下的攻击区仿真结果，可以指导超视距空战中的双机构型设计。当目标迎面来袭时，双机可保持以导弹最远攻击距离RG与目标做置尾机动时导弹能够命中目标的最远弹目距离RZ之差为间隔的纵队进攻构型。

前机在距离目标RZ时发射导弹，然后做置尾机动脱离战场，由后机负责制导，此刻后机与目标距离为RG。这可以保证我方前机的安全，且此时若目标未发现导弹，不做机动继续向前飞行，我方导弹即可命中目标；后机在前机发射导弹后与目标距离小于RG，目标在后机导弹的最大攻击范围之内，后机不仅可以为前机提供制导，还可以对目标构成威胁；该纵队构型可以使后机在制导过程中尽量远离目标，保留充足的制导时间，当后机与目标距离为RZ时，后机做置尾机动脱离战场。