具有免疫抑制和双时滞的HIV 感染模型分析
2019-11-12胡志兴
国 会,胡志兴
(北京科技大学数理学院,北京 100083)
艾滋病是由感染HIV 病毒引起的,HIV 病毒对人体的免疫系统有很强的攻击性,至今仍没有有效的药物来治愈这类传染病. 所以,近年来大量的数学模型来定量或定性的分析其传染过程,这对弄清艾滋病的传染机理以及对治疗、控制艾滋病传染具有重要的指导意义. 自Perelson 等人[1]提出经典模型,之后很多学者对模型进行了修改和完善,包括考虑潜伏期,CTL 免疫反应的影响[2-5]. Wang Y 等人又在此基础上考虑了时滞对HIV 病毒传染的影响[6-9],使模型更具有生物学意义. 很多HIV 数学模型都考虑的是饱和发生率,非线性发生率等等. Liao F 等人在此基础上考虑了细胞免疫抑制的HIV 数学模型[10-12], 但是却忽略的细胞内时滞以及CLT 免疫反应时滞对动力学模型的影响.
本文研究了具有双时滞且考虑CLT 免疫细胞抑制作用的HIV 病毒感染的动力学模型:

1 模型系统(1)的分析
系统(1)的初始条件满足:

其中
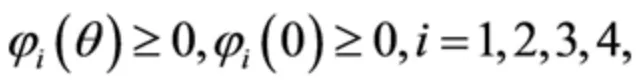

下面讨论解的非负性:由系统(1)我们可以得到


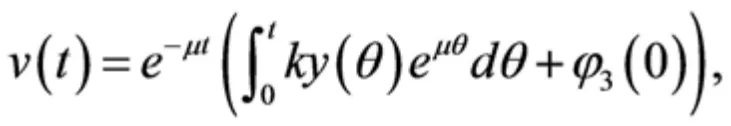
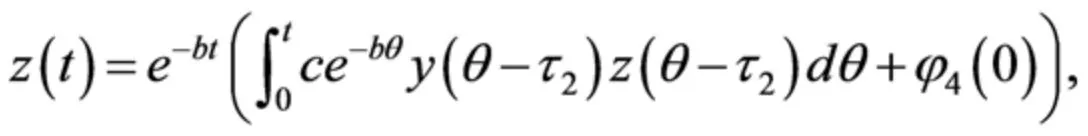


其中


2 平衡点的稳定性

即




即
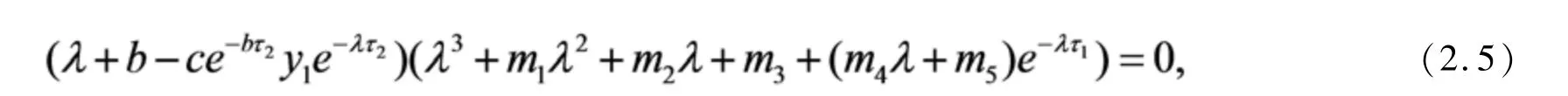
其中




的根.

因此,,




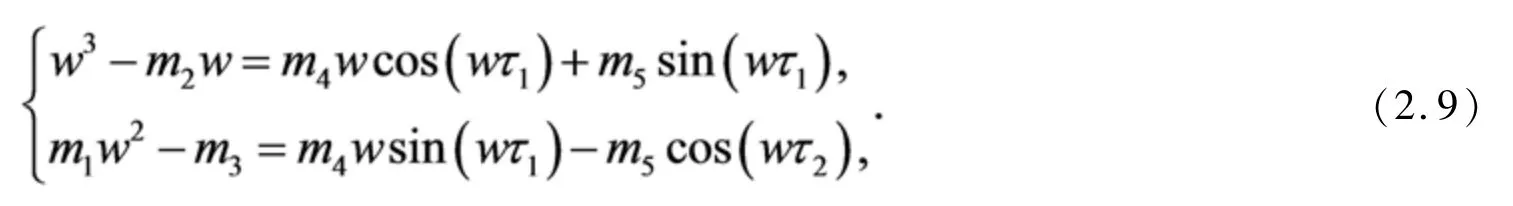


其中



根据文献[13]的命题4.8.1,有如下引理
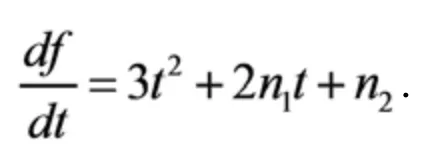
3 内部平衡点的局部稳定性和Hopf 分支

即

其中



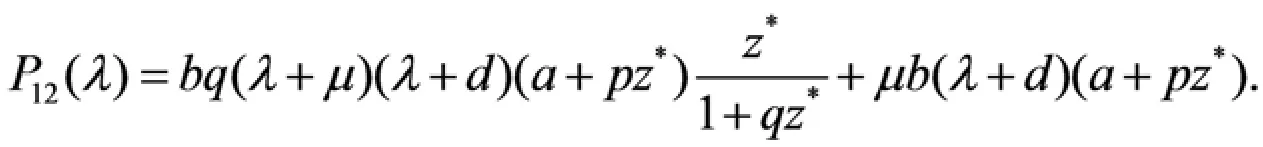
由方程(3.2)得特征方程:

其中

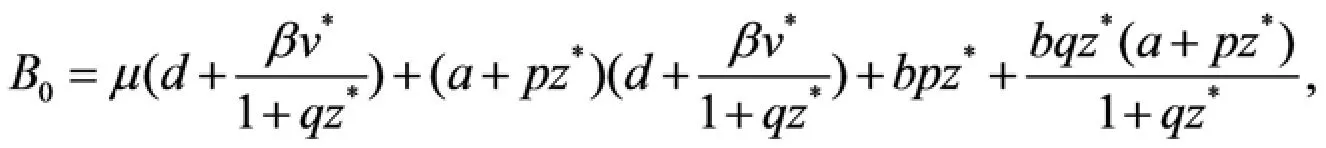


因为



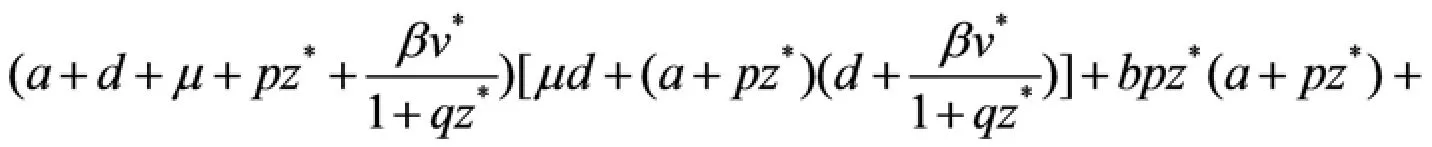

由Routh-hurwitz 判据可知,方程(3.3)仅有负实部的根当且仅当条件()成立. 所以()成立时,内部平衡点是局部渐近稳定的.
由方程(3.3)得特征方程:

其中

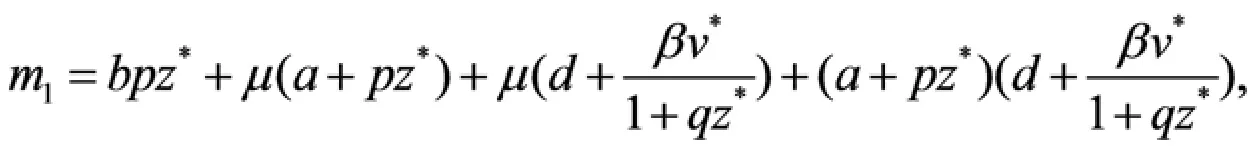





其中


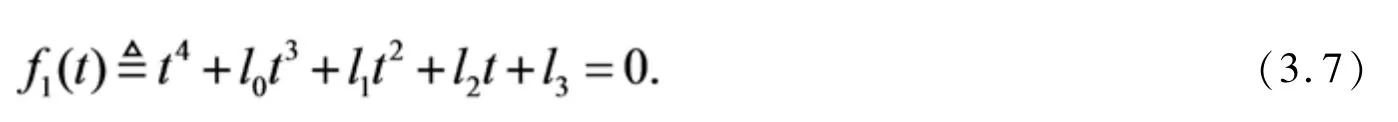
定义

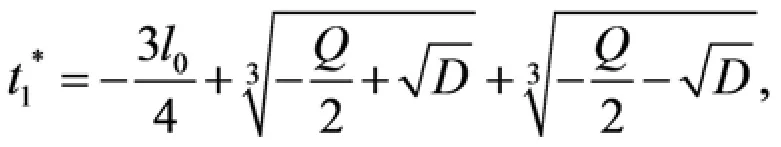

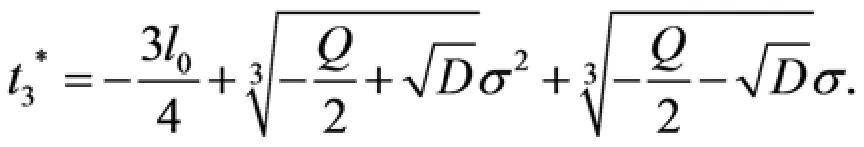
由文献[14 -15],得到下面引理.
引理3.1 如果方程(3.7)满足如下条件.
若方程(3.7)满足任一上述条件,则至少存在一个正实根.
则方程(3.7)无正实根.
不失一般性,我们不妨假设方程(3.7)有四个正实根,分别为然后方程(3.6)的四个正根分别为根据方程(3.5)得到



因此,


由方程(3.2)得特征方程:
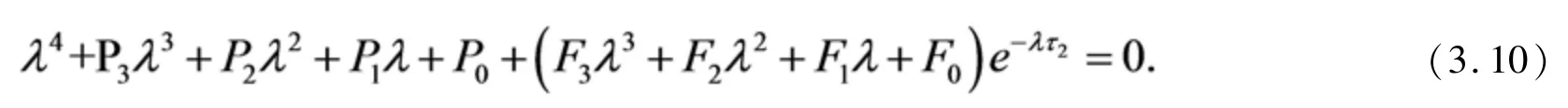
其中


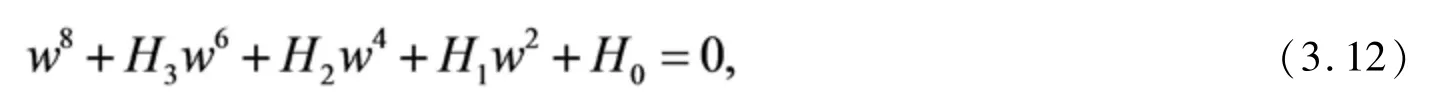
其中



由文献[15]的定理2.1 得到如下引理.
引理3.2 对于方程(3.13)有如下条件:
若方程(3.13)满足任一上述条件,则方程(3.13)至少存在一个正实根.
则方程(3.13)没有正实根.
不失一般性,我们假设方程(3.13)有四个正实根,分别为而且方程(3.12)就有四个正实根
从方程(3.11)我们可以得到:


由方程(3.11)得:

从而




假设方程(3.15)有纯虚根,带入方程(3.15),分离实部和虚部得:

解得:

其中
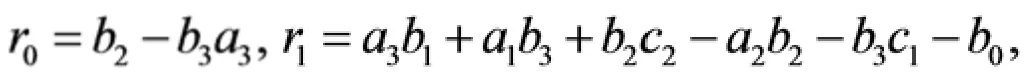


其中
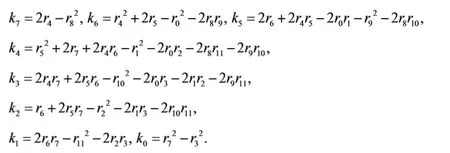

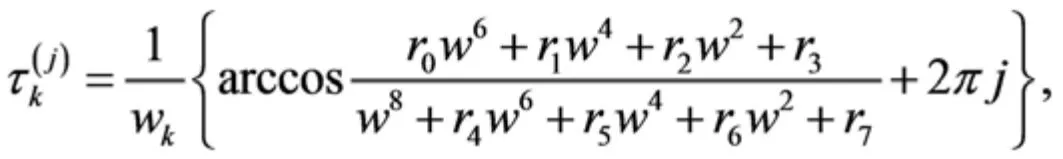

其中


因此
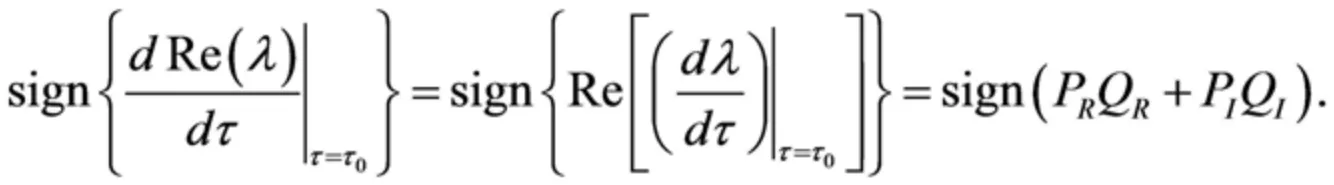
其中


其中
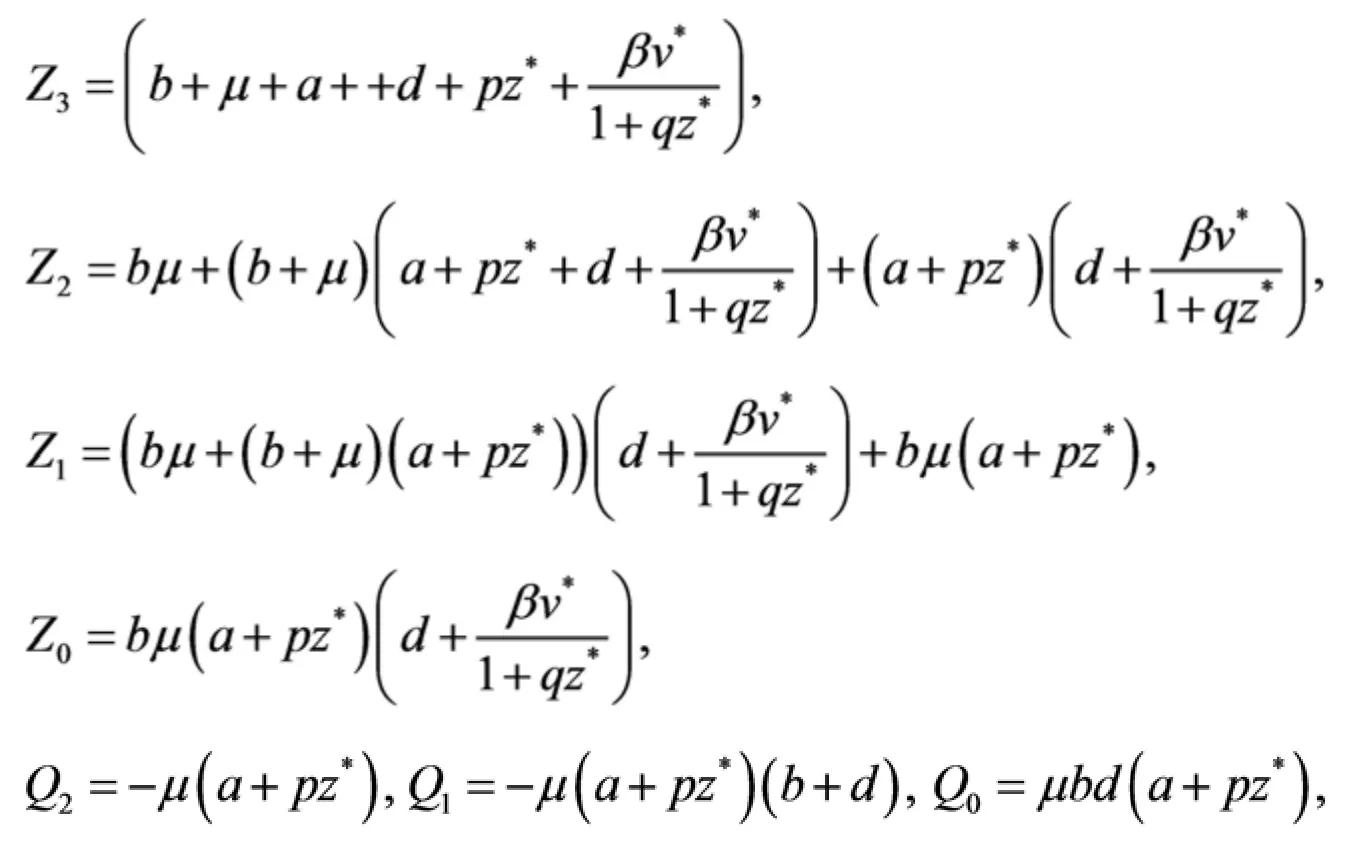


其中


将方程(3.22)中的两个方程平方后相加,得到:

其中

其中


其中
因此,
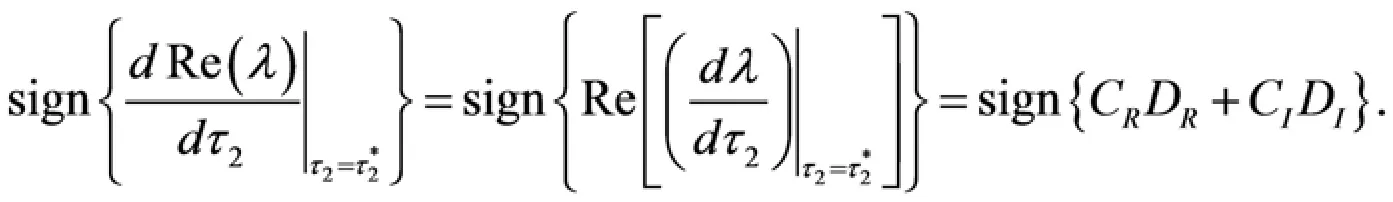
4 数值模拟
在这一部分中,通过MATLAB 对平衡点进行了简单的数值模拟.
对于情形1 选取参数的选取如下所示:

选取初值(9716,0.7961,0.0326,0.7822),计算.当时,所选参数满足情形1,此时内部平衡点是局部渐近稳定的,如图1 所示:

图1 时,渐近稳定Fig.1 is locally asymptotically stable when
在情形2 中选取如下参数:


图2 时系统的相图Fig.2 Phase diagram of the system for
在情形3 中选取参数如下:
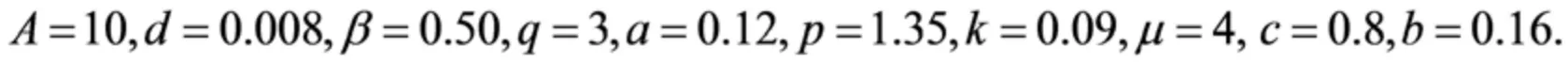

图3 时系统的相图Fig.3 Phase diagram of the system for
在情形4 中选取参数如下:

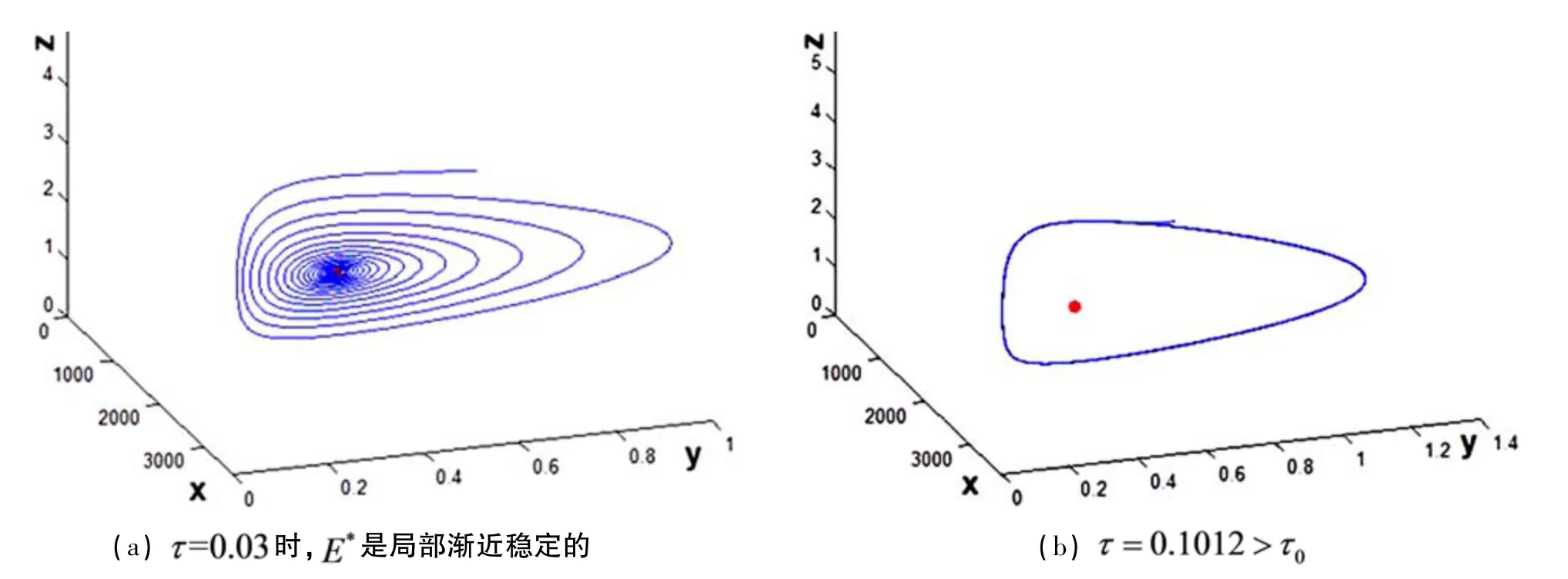
图4 时系统的相图.Fig.4 Phase diagram of the system for .

图5 时系统的相图Fig.5 Phase diagram of the system for
5 结论
本文建立了具有免疫抑制及两时滞的HIV 病毒感染模型. 主要由Routh -Hurwitz 判据等方法证明了两边部平衡点产生影响.将两时滞作为作为分支参数分析了不同情形下内部平衡点Hopf 分支的存在情况,结论表明时滞可能会使正平衡点扰动,进而产生周期解.由于没有临床医学数据,没有具体研究病毒复制的抑制率对免疫细胞浓度的影响.事实上,未来还有更复杂的模型值得考虑,比如考虑细胞的Logistic 增长,空间扩散等.
