线性ADRC 在永磁同步电机DTC 系统的应用研究

汪华章，李明洋，姜承忠

(1.西南民族大学电气信息工程学院，四川 成都 610041；2.威马汽车科技集团有限公司，四川 成都 610100)

与传统的电励磁同步电机相比，永磁同步电机(PMSM)结构简单、运行可靠、损耗小、效率高，因其形状和尺寸的特点，可以灵活多用，在伺服系统中得到广泛的应用[1-2].1985 年德国鲁尔大学Dpenbrock 教授第一次提出了直接转矩控制理论[3]，由于它没有矢量控制复杂，所以很快受到国内外学者的关注[4-7].

直接转矩控制方法实现了磁链和转矩的双闭环控制.在传统DTC 系统中，逆变器的实际开关频率一般达不到要求，使得一个数字控制周期中所选用的有效电压矢量无法与期望的电压矢量一致[8]，通过实验发现，将滑膜控制引入控制系统，能有效解决传统DTC 存在的转矩和磁链脉动较大、逆变器开关频率不恒定等问题.

自抗扰控制是一种新型控制技术，能自动检测并补偿被控对象的内外扰动[9-11].此外，其不依赖被控对象的数学模型的特性，使得其应用中更易实现.在扰动明显影响系统的最终输出前，主动从被控对象的输入/输出信号中提取扰动信息[12]，并及时给出控制信号将扰动消除，具有较强的适用性和鲁棒性.

1 永磁同步电机的直接转矩控制系统方案

设计的永磁同步电机直接转矩控制系统如图1 所示，其中线性ADRC 为系统控制器，结合Super -twisting滑膜控制器以减小直接转矩控制系统的转矩脉动，增加系统的鲁棒性.引入磁链估计环节，对系统的磁链输出进行实时的估计，并及时补偿.

图1 基于线性自抗扰控制的永磁同步电机直接转矩控制系统方案Fig.1 DTC system of PMSM based on LADRC controller

1.1 三相PMSM 直接转矩控制

当三相PMSM 的数学模型实现完全解耦后，电磁转矩方程可写为：

根据式(2)可以看出，三相PMSM 中转矩增量与磁链和转矩角增量的关系，即在一个控制周期中，由于机械时间常数远远大于电气时间常数，其转子位置变化很小.故可通过控制定子磁链迅速改变其转矩角，使转矩快速变化和幅值稳定.

1.2 线性自抗扰控制器设计

控制器的阶数设计依赖于被控对象的阶数，被控对象一般为二阶，所以本文将针对二阶被控对象设计三阶控制器(实际应用中，线性ADRC 比对象高一阶，用于对系统的扰动及噪声进行补偿). 考虑存在非线性系统.其中是外部扰动，是系统的总扰动(包括系统建模不确定性在内的内部扰动和外部扰动之和)，是控制输入，是控制系统输入增益，为系统输出.将作用于开环系统的加速度的实际作用量扩充为一个新的状态变量，记为. 假设可微，并有，且有界.则上述非线性系统可扩张成新的非线性系统如式(3)：

式(3)的状态空间可以表达为：

线性扩张状态观测器是基于状态空间模型的状态观测器，是为了简化参数调试的复杂性，减少需要调节的参数数量，提出的一种设计方法[9，13-14].根据式(4)可以设计扩张状态观测器如式(5)：

传统PID 组合实施控制器的积分环节是为消除常值扰动下的稳态误差，由于ESO 能够实时估计并补偿内、外部扰动，故线性状态误差反馈控制率就简化为PD 组合，舍弃积分调节器，其形式为：

结合工程应用，LADRC 控制器中带宽参数整定为：

自抗扰控制理论的实质就是对系统的扰动实时估计和动态补偿，其控制器对扰动的抑制能力受噪声和采样频率的限制.将自抗扰控制线性化，使得控制器参数减少，工程应用中，为提高对扰动的抑制效果，观测器、控制器带宽参数的选择可以遵循以下几点：1)控制器的带宽要高于系统要求的带宽；2)观测器带宽应该低于采样频率；3)观测器带宽与控制器带宽满足：或.

2 仿真研究

为验证本文所设计的二阶线性ADRC 控制效果，以及理论分析的正确性和转矩调节器设计的合理性，对定子绕组为三角形连接的永磁同步电机在Matlab/Simulink 环境下对系统进行了仿真研究.

在实际应用中，系统与控制器均存在饱和特性，因此须在控制器模型中须引入相应的限幅环节以限制输出.线性扩张观测器(LESO)中参数分别设置为：

线性ADRC 控制器仿真与本文设计的基于线性LADRC 的永磁同步电机DTC 系统仿真如图2、图3 所示：

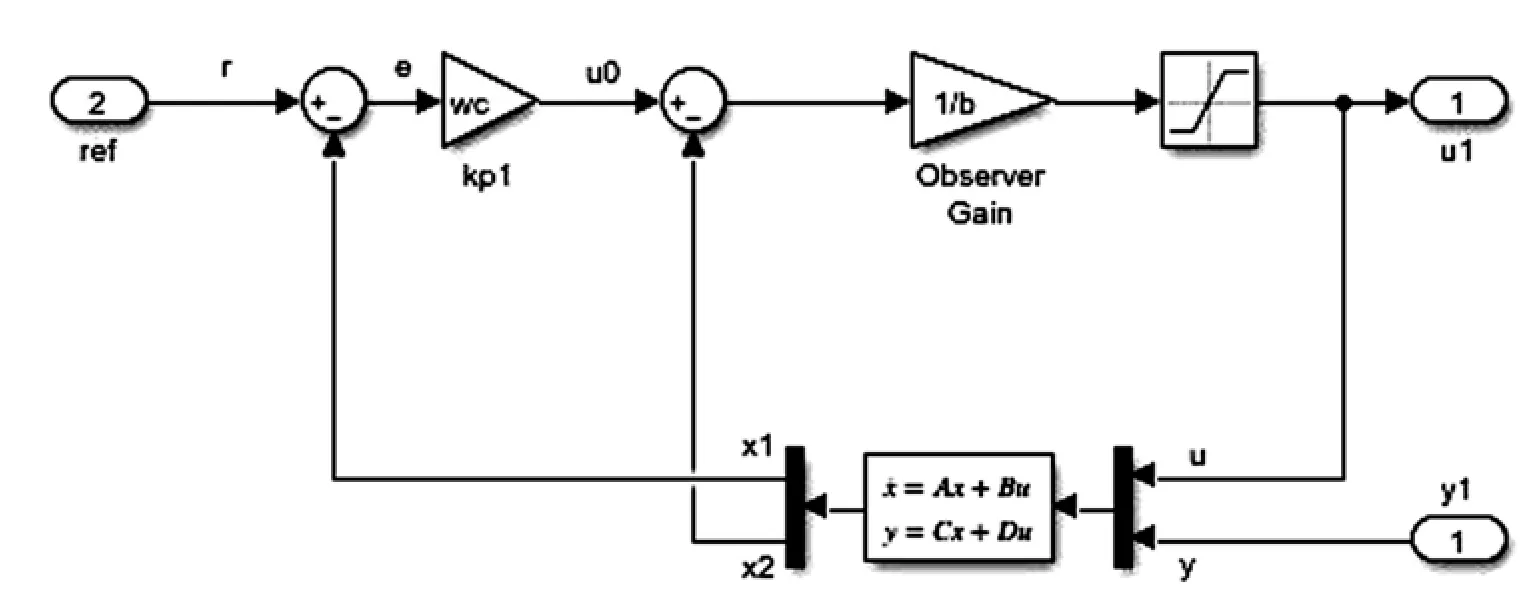
图2 线性ADRC 仿真图Fig. 2 Linear ADRC simulation

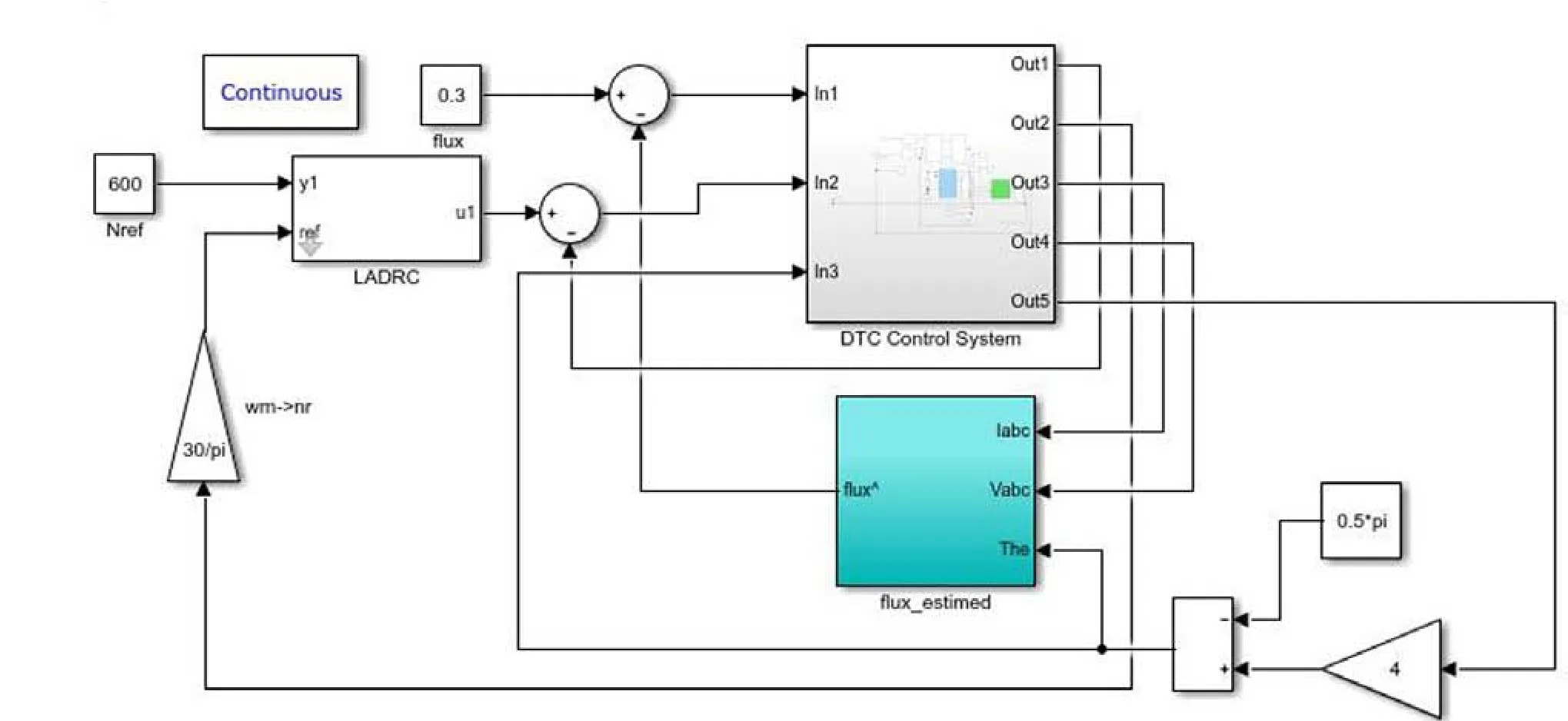
图3 基于线性ADRC 的永磁同步电机DTC 系统仿真图Fig.3 DTC system simulation of PMSM based on linear ADRC

仿真结果如图4、图5 所示.本次实验不增加任何负载，目的在于测试设计的控制系统的响应速度及其达到稳态时的误差.

图4 空载启动电磁转矩图Fig.4 No-load starting torque

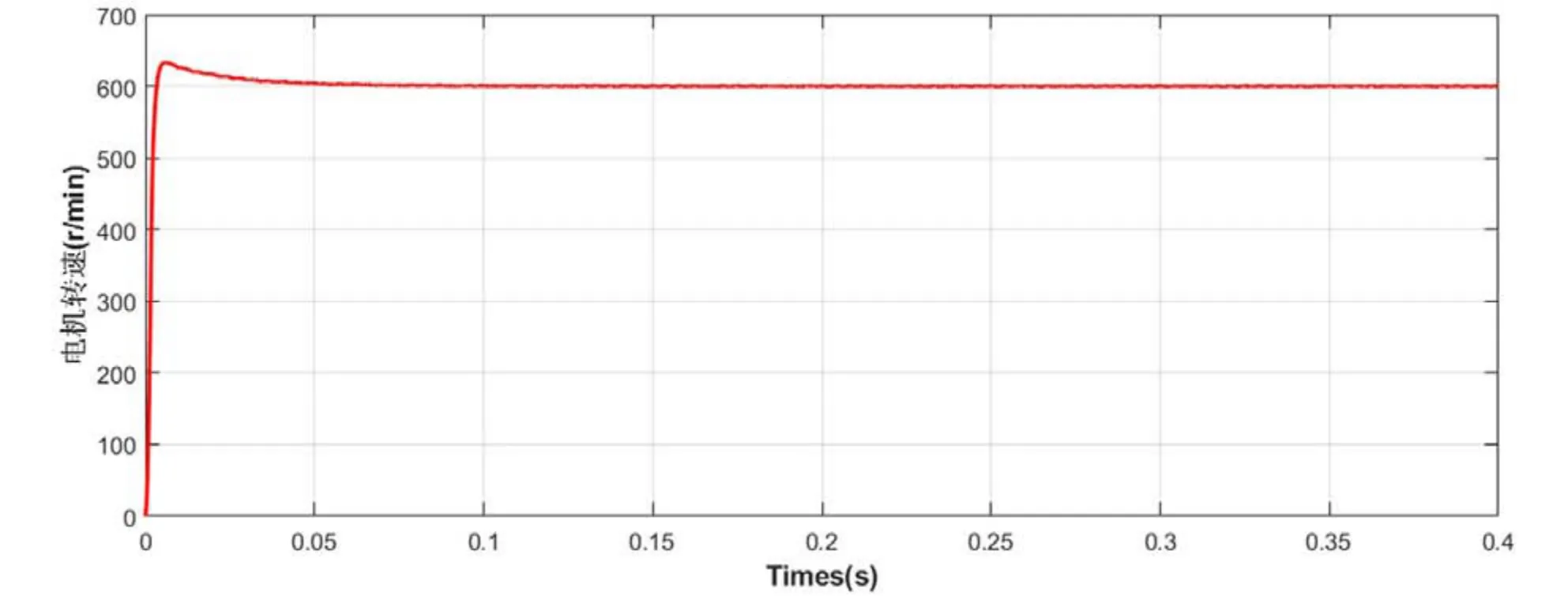
图5 空载启动电机转速Fig.5 No-load starting motor speed

电机在启动的瞬间，电磁转矩有骤增现象，永磁同步电机其特定的结构允许在短时间内有该现象发生；从电机转速随时间的变化曲线可以清楚的看到，系统存在超调现象，并在0.05 s 内达到平稳.根据图4、5 中可以证明本文提出的控制方案合理，并且具有快速的动态响应.

图6、图7 分别为传统DTC 系统、本文控制系统的磁链相位曲线. 图6 中，磁链有一定的环宽，其半径在0.295 Wb处波动，因此磁链脉动较大.但在本文设计的控制系统中，定子磁链圆的环宽明显变窄，磁链脉动减小.

图6 磁链相位变化曲线Fig.6 Flux phase curve

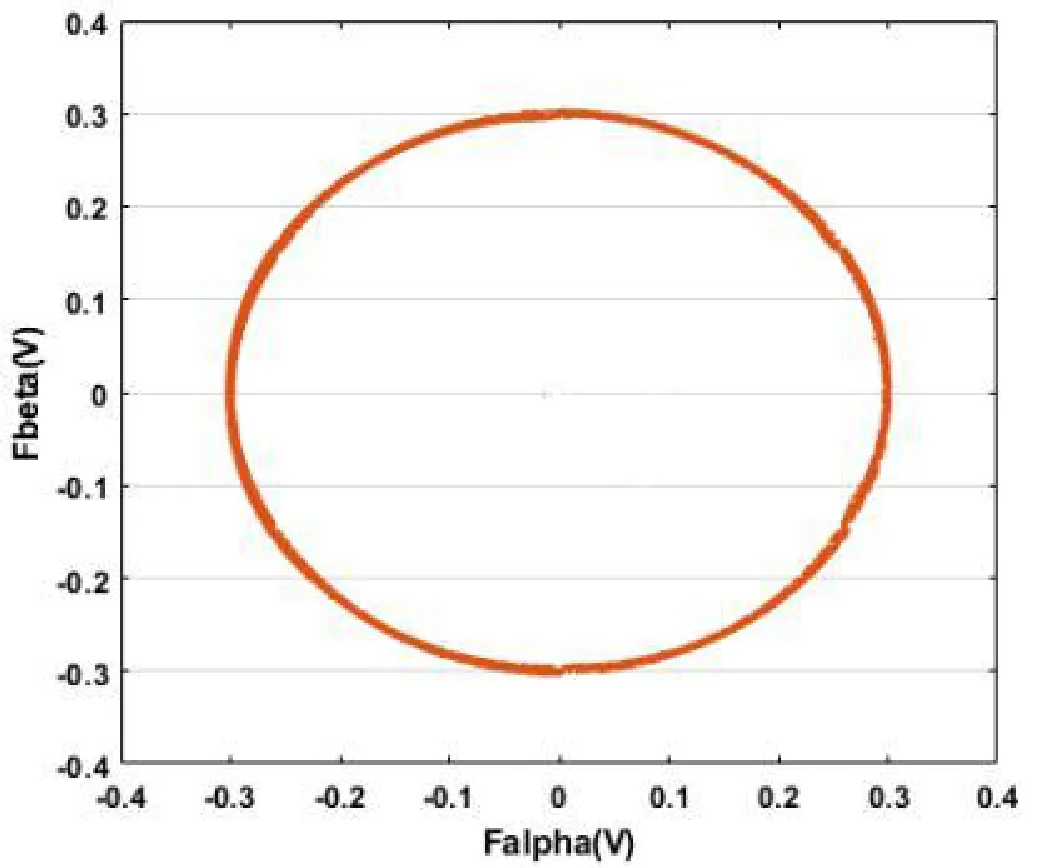
图7 磁链相位变化曲线Fig.7 Flux phase curve

图8 电磁转矩Te变化曲线Fig.8 Curve of torque

图9 三相电流变化曲线Fig.9 Three-phase current change curve

图10 传统DTC 系统中电机转速变化曲线Fig.10 Motor speed change curve in traditional DTC system

图11 线性ADRC 控制器中电机转速变化曲线Fig.11 Motor speed change curve in LADRC controller

在图8 的电磁转矩Te变化曲线可以看出，仿真时在0.2 s 突然给系统添加负载，电磁转矩增加，短时间内回复平稳；图9 为在改仿真条件下，三相电流Iabc的变化曲线，在0.2 s 突然给电机引入负载，电流输出逐渐增大，电机输出扭矩增加，在0.4 -0.5 s 之间就达到稳定，可以说明线性自抗扰控制器在本文设计的系统中对波动图有良好的抑制和消除的作用.图10 为传统DTC 系统中的电机转速变化曲线，图11 为本文设计的基于线性自抗扰控制器的DTC 系统中的电机转速变化曲线，在0.2 s 添加负载后，电机转速降低，在短时间内达到稳态，并且稳态误差为2.5%.

3 结论

本文设计的永磁同步电机直接转矩控制系统，引入自抗扰控制器，弥补了由单一超扭曲滑膜控制带来的系统惯性大，提高了自适应能力，增强了鲁棒性，且设计时不依赖系统的精确模型.在Simulink 环境下进行仿真，由仿真实验结果可以看出，本文设计的永磁同步电机直接转矩控制系统，具有良好的动静态性能.在空载启动时，系统响应速度快，超调量较小，达到稳态时，系统误差也较小.当系统负载变化时，电机在较短的时间内恢复设定值，误差仅为Nref±2.5%.