井中地震数据中值滤波方法研究

王 旭，赵 冲

（西安石油大学，陕西 西安 710065）

在井中地震勘探中，自下而上的上行波、自上而下的下行波甚至包括横波，这些井中地震波场中常见的地震波基本都可以被接收到。与常规地面勘探相比较而言，它拥有较强的识别能力、并且它的精度很高、成像效果很好等特征，能够较好的满足现今地震勘探的较高的精细化要求，并且可以作为对常规地面地震勘探的一个很好的补充。正是由于井中地震技术所具有的这些优点，使得井中地震技术越来越受到青睐。井中地震数据十分复杂，包含非常丰富的波场信息，如想由此得出高质量的成像效果，必须对原始的井中地震数据进行波场分离。波场分离的方法有多种，本文重点探讨中值滤波波场分离技术。

1 中值滤波方法原理

中值滤波技术在数字处理方面的应用是比较早的，并且在地球物理资料数据处理中有着广泛的应用。中值滤波技术可以归结为一类非线性平滑技术，它是以数学当中的排序理论为基础的，又被称为中位数法，它用一个设定好的区域对一系列数据不断地做平滑，把这个区域中的数据排序并找出中间值并输出。主要原理步骤为：

1） 任取一个像素，以该像素为中心点选一个区域（最好正四边形）；

2） 然后对处于该区域中的各个像素的灰度值数据进行排序处理，然后把这个区域内的中间值取出来，用这个值来代替中心点像素灰度。通常将这个区域称之为窗口；

3） 利用中值滤波算法，让滤波窗口在图像中上下左右不断逐点进行移动，对图像作平滑处理，这样就对该图像完成了一次中值滤波处理。

对于一个一维数组（x1，x2，…xn） 来说，将这n 个数据进行排序处理，得到一新的序列（x1≤x2≤…xn），之后对排序的数据进行取中值，见公式（1）：

其中y 称为序列的中值。

实际实现时一般选取长度为L=2n+1 的滤波窗口，其中n 为正整数。将窗口在整个需要处理的数据上来回移动进行处理，中值滤波的输出就表示的是滤波窗口中心处的值用该窗口的中值来取代，表达式见公式（2）：

从定义中看出，因叠加原理已不再适用，由此可知中值滤波技术是一种非线性滤波方法，当滤波窗口的宽度为2n+1 时，在信号序列中其宽度不大于n 的脉冲便会被该方法去除掉。但再标准的中值滤波方法也无法克服其自身的缺点，由于它是对所有数据采取统一的处理方式，这种方法不但改变了噪声信号的值，同时也改变了信号点的值，并使噪声在其领域内进行传播[1-3]。

利用中值滤波进行井中地震波场分离的原理可以表述如下:

在记录的波场中，上、下行波的视速度一正一负的，满足正负符号差异特性，故此在地震记录上，它们表现出的同向轴斜率存在不同之处的，就是这样的特点，让中值滤波方法才能在井中地震波场分离中有了用武之地。它一般有以下的几个步骤：

1） 首先要做的就是将下行波沿着水平方向拉平，我们把这一步称之为时移，它所遵循的原则是将数据按照初始时间校正到相同的时间；2）之后沿水平方向作中值滤波处理，如图，经过处理后水平排齐的下行波振幅得到增强。当然此处我们只要选择了合适的滤波跨度，就能达到增强上行波、削弱下行波进而分离出上行波的目的；3） 接下来要对中值滤波处理后的数据做反向时移，这一步是基于原来的时移时间来做的，这时整个波场就只表现下行波场；4） 最后用原始地震数据与得到的滤波后的数据进行做差，即可得到分离出的上行波场。

2 中值滤波算法实现

对所设计的合成地震数据进行中值滤波处理，所选取的滤波方向为道序方向。为避免窗口选取不合适所带来的边界效应，进行了两次滤波处理。在运用第一个跨度滤波后，由于道数可能不能整除所选用的跨度，因此会存在剩余道数不能被处理，存在余数边界问题。此时，需要对剩余地震道继续进行滤波处理，选择第二个跨度对剩余的所有道进行滤波处理。第一次的滤波跨度（key1）选择是测试选择的滤波窗口，处理效果会存在一些边界效应，还留有一点“尾巴”，这种情况可能的原因之一就是道数与滤波跨度不能整除，基于此，本文中所用到的方法是以剩余地震道数为第二次滤波跨度（key2） 对剩下的地震道再进行了一次性处理。经过两次的中值滤波处理，处理后的效果将会明显改善。在进行完滤波处理之后，需要用原始地震记录与滤波后的地震记录进行做差处理，才会得到包含丰富地层信息的上行波场。图1是中值滤波算法设计的流程图。

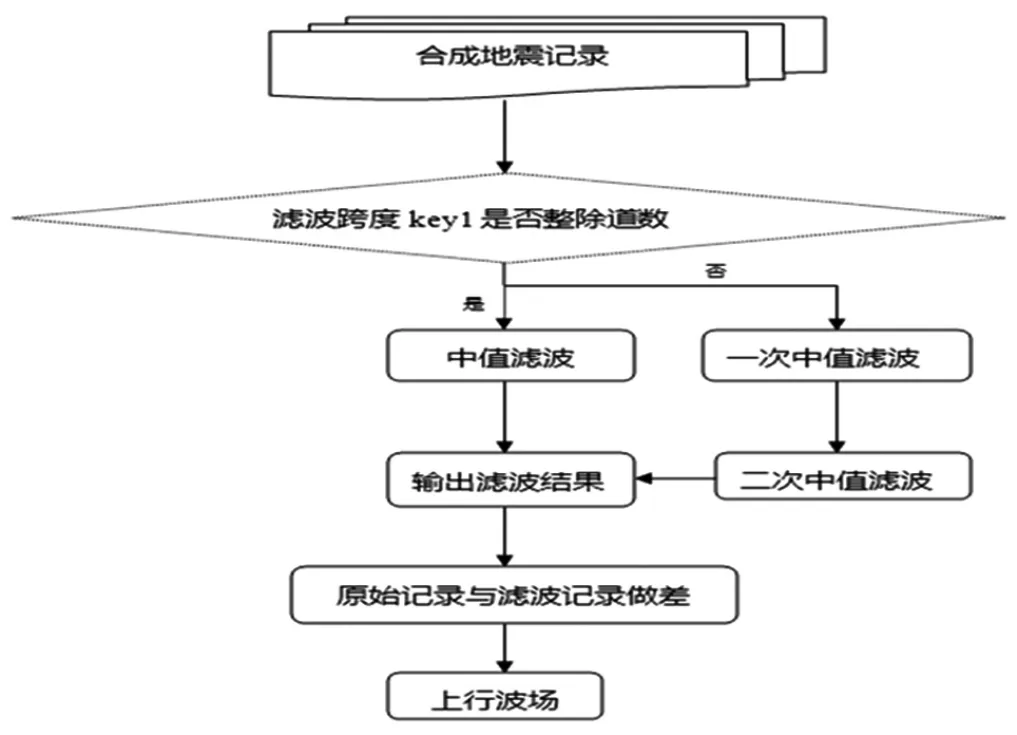
图1 算法流程图

3 算法应用结果对比分析

利用前文所设计的中值滤波算法对几种类型的合成地震数据进行滤波处理，分析其应用后的效果并且讨论了中值滤波方法的跨度选择问题。主要做了以下几个方面的结果分析对比，针对不同类型的合成地震数据的滤波效果进行分析、同一合成地震数据的不同滤波跨度效果的对比分析以及同一地震数据的不同子波长度的最佳滤波跨度选择研究。通过这些比较，可以测试本文所介绍的中值滤波算法的应用效果，理解选择合适的滤波跨度对中值滤波效果的影响和随着子波长度的变化情况，如何才能选择最佳滤波跨度使得中值滤波效果达到最好。最后将本文的算法应用到实际的地震数据进行应用，总结其在实际应用方面的问题。

3.1 理论井中地震数据的波场分离

如图2（a） 所示，理论地震数据的上行波场为两条交叉的倾斜同向轴，最开始还是用初始模型的11 点滤波跨度来进行滤波处理，但处理效果不佳（主要表现为上行波场没有完全滤除干净，仍有一小部分的“剩余波”），经过滤波跨度的改变调试之后，在滤波跨度选择为17 点时，分离效果才有了比较大的改善（见图2 (b)、 (c)）。

3.2 实际地震数据资料测试

为了测试本算法在实际地震记录的应用效果，选取了某工区采用零偏移距井中地震地震数据进行测试。从原始剖面图3 (a) 中以看到，该地区井中地震波场信息丰富，其中上行波、下行波交叠在一起，而且下行波的能量明显强于上行波。

由图3（c） 看出，应用本文的中值滤波方法对实际地震数据进行处理，能够较好的分离出上、下行波，得到了较为理想的效果，较好的保留了有用的波场信息。到的下行波场；c. 波场分离得到的上行波场。

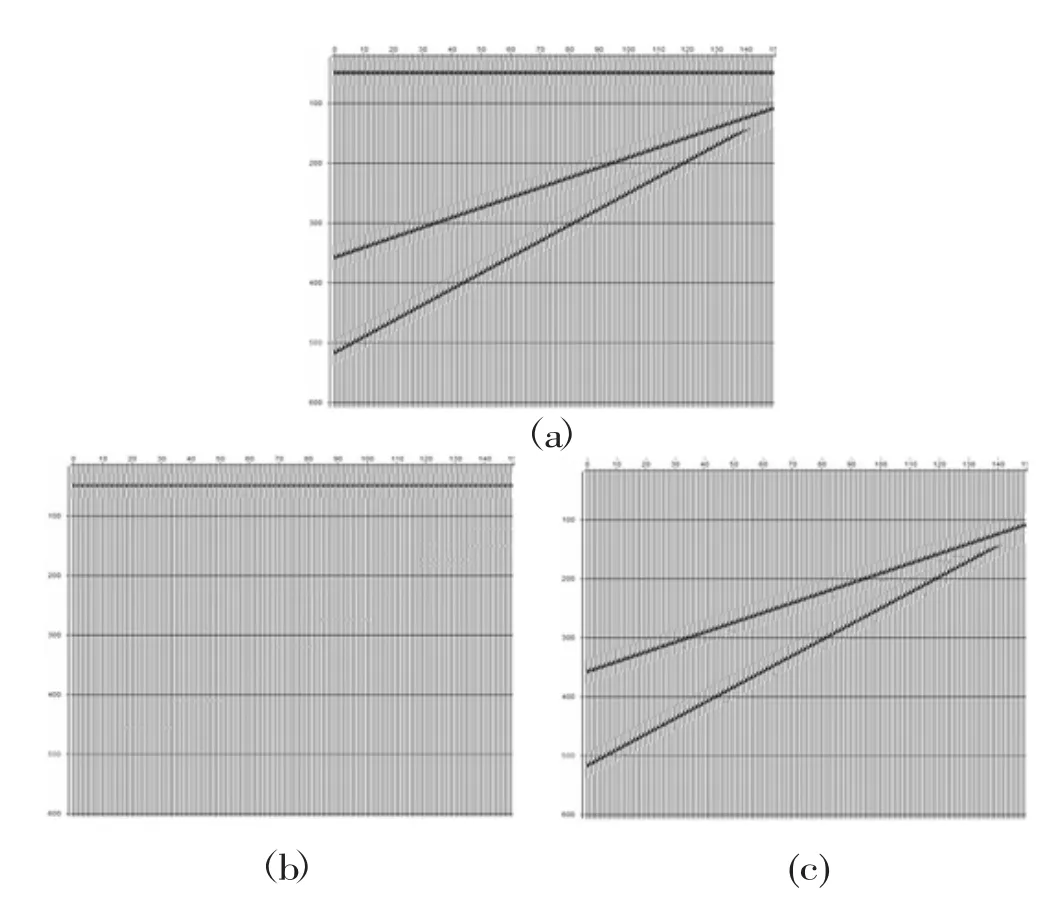
图2 理论地震数据的波场分离

4 结语

通过本文的研究得到了以下的结论：

1） 对于一般的比较简单模型，中值滤波可以取得较好效果，方法较简便易实现效率高，对于简单构造区域是比较适用的；2） 但对于复杂区域，只用中值滤波方法取得的效果往往不是很理想，通常还要结合其他波场分离的方法来对复杂地区的井中地震波场进行处理；3） 中值滤波的效果主要在于滤波跨度的选取，跨度太小，不能达到滤波的要求；而跨度取得太大则会使平滑效应严重，造成部分有效信号被压制掉。因此，滤波跨度的选择是关键，并且通过之前的对比，波场的变化或子波长度的变化都会影响最优跨度的选取，其中子波长度与跨度的选取往往成正比关系。

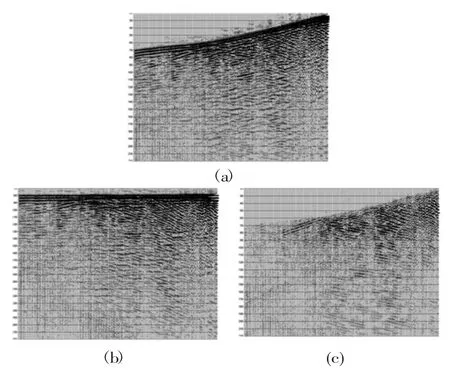
图3 实际地震数据的波场分离