基于修正Z变换法的数字控制系统

杨 栩

（成都师范学院物理与工程技术学院，成都611130）

0 引言

数字控制系统中存在数字部分和连续部分，系统中含有采样信号，而被控对象大多为连续信号，数字控制系统可以等效为一个数字系统，用Z变换法来分析系统，系统输出响应为周期采样点上的输出。采样周期之间的输出信息很难获得，如果要得到更多的输出点信息，一般通过改变采样周期的大小来实现。但是采样周期T不能随意改变，减小T可以获取更多的采样点信号，信号恢复精度越高，但是T过小，会使执行效率下降，增加运算，在工程实践中也不允许T过小，这会给信号恢复和分析带来困难。

修正Z变换法在不改变采样周期T的前提下，通过对系统输出增加一个虚拟延时环节，在采样周期内任意延时，通过修正Z变换法，能得到任意时刻的输出，从而实现信号的连续输出。

1 数字控制系统

在计算机控制系统中，控制系统由数字部分和连续部分构成的混合系统，在系统中有离散采样信号和连续信号，等效为数字部分和连续部分。数字部分表示计算机控制算法，输入和输出皆为离散序列，用D(Z)表示；连续部分等效为连续被控对象和零阶保持器串联构成。计算机控制系统结构框图如图1所示。

图1 数字控制系统结构框图

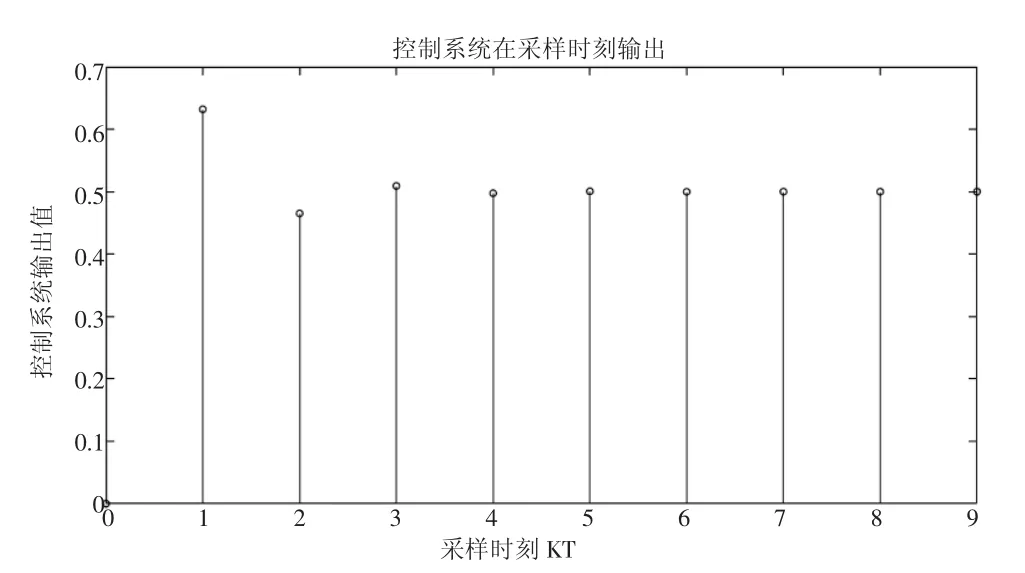
图2 控制系统在采样时刻输出值

系统分析时，只能得到控制系统在采样周期整数倍时刻的输出序列C（k），而被控对象大多是连续部分，实际输出是连续信号。为了能补齐采样点时刻之间的连续输出，可以采用修正Z变换法获得非采样点之间的输出。

2 修正Z变换法

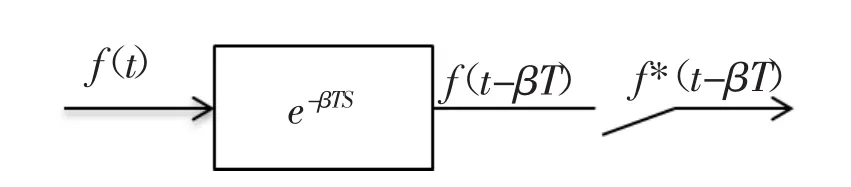
图3 输入信号 f（t）延时 βT（0＜β＜1）

号f（t）的修正Z变换F（Z，m）表达式为式（1）：

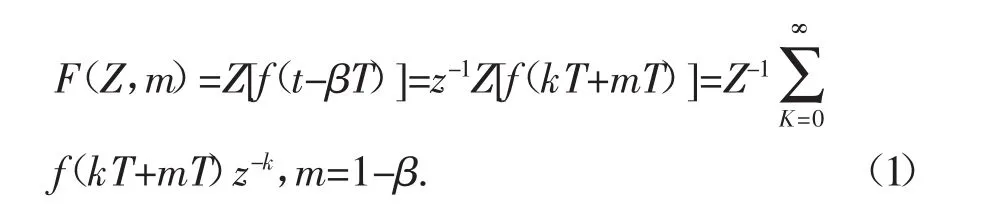
对于用F(S)表示的连续函数，修正Z变换表达式为式（2）：

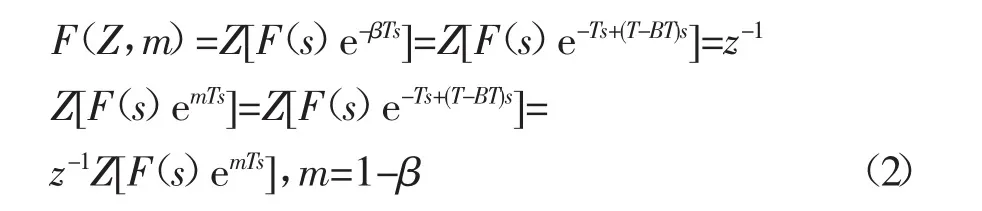
当m=0时，β=1，相当于信号延迟一个采样周期；当m=1时，β=0，若f(0)=0，则修正Z变换为一般Z变换。

3 修正Z变换法在数字控制系统中的应用

系统输出为连续信号，为了统一数字连续部分，可以给输出加一虚拟滞后环节（0＜β＜1），等效为时域的延时环节，计算机控制系统结构框图如图4所示：零阶保持器和连续系统等效为连续系统G(S)。

系统输出为式（3）：

图4 计算机控制系统结构框图

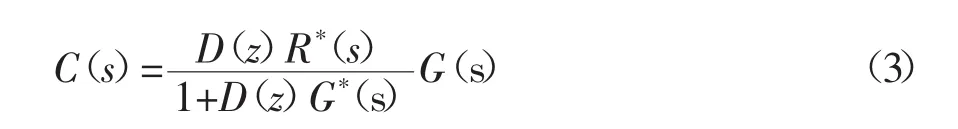
虚拟滞后环节e-βTs（0＜β＜1），Z变换为修正Z变换 C（Z，m）表达式为式 4（m=1-β）。

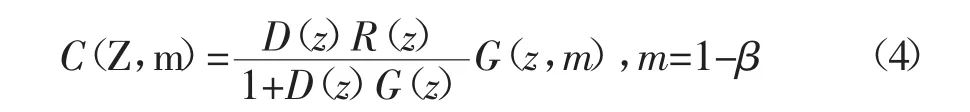
采样系统经过修正Z变换后的系统函数为式（5）

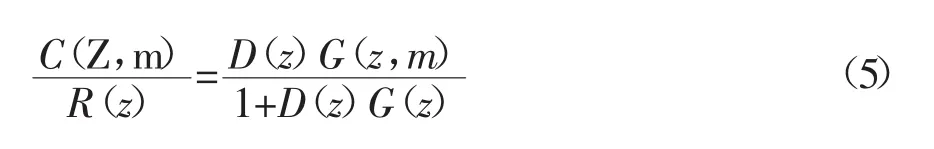
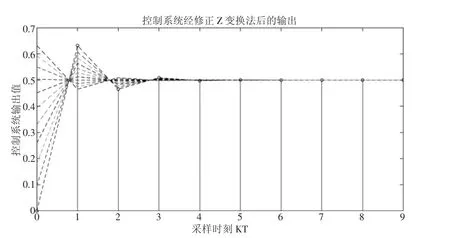
图5 控制系统经修正Z变换法后系统输出值

其中，红色圆圈处值为控制系统在整数倍采样周期时刻的输出值，不同颜色虚线表示控制系统经βT(0≤β≤1)延时后系统输出，通过延迟不同的时间，可以得到非整数倍采样周期时刻的输出信号。当β=1，输出与非修正Z变换输出一致，当β=0，输出恰好为非修正Z变换的下一采样点值，当0＜β＜1时，输出为非整数倍采样周期时刻的值，其值大小介于非修正Z变换的两个采样点值之间，本图中β取值步长为0.1。

为了更直观地观察控制系统非周期整数倍时刻的输出值，对控制系统采用修正Z变换法，延时时间步长取更小的β为0.01，将系统输出值与采样时刻对应，可以获取更多的非周期采样点上的输出值，控制系统经修正Z变换法后系统输出如图6所示。

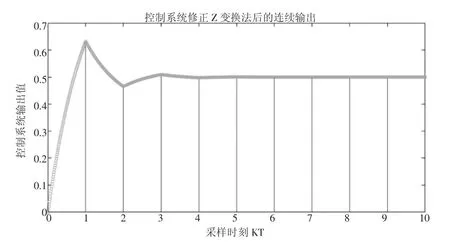
图6 控制系统经修正Z变换法连续输出响应

4 小结

通过仿真图可以看出，系统输出为连续输出，除了采样点处有值外，采样点之间也不失真的还原了连续系统的输出。本方法达到了预期效果。修正Z变换法在不改变采样周期T的前提下，通过对系统输出增加一个虚拟延时环节，能够得到任意时刻的输出，从而实现信号的连续输出。