初中数学教学中有效问题情境的创设

摘 要：问题情境在初中数学教学中发挥着重要的作用，一个良好的问题情境能够在很大程度上提升课堂教学效率。基于此，文章重点结合了一些教学案例，对其问题情境创设方式进行了综合分析，以供参考。

关键词：初中数学;问题情境;方法

中图分类号：G633.6

文章编号：2095-624X（2019）21-0039-02

一、问题情境概述

1.意义

创设问题情境能够较大程度上调动学生的学习积极性，激发其自主学习能力，激活思维，使其掌握学习数学的方法和思维策略，最终将数学知识灵活地运用到实际生活之中。问题情境的创设将原先教师灌输式的教学模式做了改变，它留给学生更多自主学习的空间与时间，使大家从原先的被动学习逐渐转变为主动参与学习，同时促进了创新能力及思维的提升[1]。

2.良好问题情境的判断

通常情况下，好的问题情境可以促进大家对数学原理、概念以及公式和数学思想进一步的理解，同时还能够调动大家的生活经验与一些数学背景，进而有效激发学生对数学学习意义的思考，让大家通过问题情境创设、建立数学模型以及解释与应用活动学会数学知识。所以教师需要有效把握学生的发展情况，并与学生自身的知识基础相互联系起来，并且还要保证不会和新知识形成冲突[2]。

二、创设方法

1.要有具体性和明确性

创设问题情境最根本的一个原则就是给出的问题必须具有非常明确的目的，并且始终与教学目标相关联，同时还要具体，在表达的时候需要简洁清晰。只有让大家理解清楚问题才有可能引导其进行思考并解决问题。

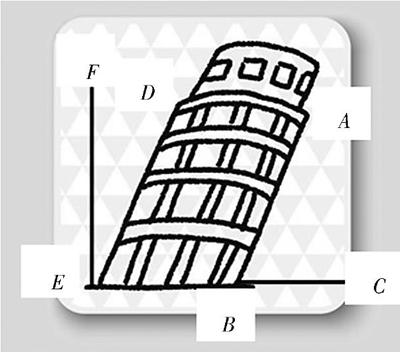
例如，在教关于“余角”概念的时候可以设计出这样的一个情境。将著名的比萨斜塔引入，如下图。图中∠DEF和∠ABC是描述比萨斜塔垂直方向与水平方向的，那么大家想一下∠DEF和∠ABC之间有着什么样的数量关系呢？

2.要具有一定启发性

创设问题情境本身还需要具有一定的启发性，要引导学生进行联想、猜想。另外，启发性的实现必须建立在开放性的基础上。可以是问题开放，可以是条件开放，也可以是结论开放，又或者是解题的策略开放。除此之外，问题还应该具有相应的挑战性，以此激发学生的学习欲望和认知冲突，从而促进学生可以主动积极地进行探究。教师需要在分析教学内容和学生学习状况的前提下，依照其教学目标设计出让学生本身认知与新知识产生矛盾的具有挑战性的问题。

例如，在学习“相似形”的时候，可以给大家先出示两张是同一个底片但是大小不一样的照片，然后再出示一个大小不一样的30°三角尺和国旗上面的五角星等内容。然后向大家提问：这些图形具备什么样的特点？由于本身材料自身具有极大的丰富性，所以大家就能够很快归纳出来其大小不一，但是形状相同的规律。这样不但可以有效引入新课，还能够让大家一下就将相似形的属性掌握清楚。

3.要具有一定合理性

在创设问题情境的时候还必须与实际的客观规律相符合，同时还必须与大家的认知规律相符合，进而有效激发学生学习的兴趣，以促使其能够主动参与到学习之中，做课堂的主体。

例如，在教“同类项”的概念时，可以事先将讲台上或者某一个学生的书桌打乱，然后让大家思考应该要怎样进行整理;或者拿出一副扑克牌抽出一张，让大家思考缺少的那一张应该是哪一张。这样一来大家就会感觉到“归类”本身就是生活中的事物，进而给同类项概念的学习奠定良好的基礎。这种从学生实际生活入手的情境更能够激发学生的学习兴趣，并将生活当中的分类思想引入数学学习之中去。

4.要具有一定发散性

在创设问题情境的时候还应该从不同的角度出发提出问题，让大家可以运用不同的方式去解决问题，进而达到发散思维、开拓思考空间的基本目的。

5.要具有一定真实性

在新课标当中表示学生所学习到的数学内容必须是有意义的，具有挑战性的，同时也是现实的。所以在创设问题情境的时候就需要将大家最熟悉的生活实践当作问题的背景，让大家从中抽象出数量的关系，从而有效解决问题。其情境必须具有一定的真实性，只有保证情境的真实性，构建的知识才会更可靠，最终收到预期效果。

例如，在教“立体图形的展开图”这一节内容的时候，可以设计出这样一个问题情境“在一面墙壁下方有一只壁虎，墙壁上方有一只蚊子，壁虎想要用最快的速度吃掉蚊子，那么应该走哪一条路？”这种趣味性的问题情境不但可以有效激发学生的学习兴趣，还能够激发其探索的欲望。

6.要具有一定层次性

教学的时候还需要将新知识作为核心，促进知识的迁移。同时还应该根据不同层次的学生提出不同层次的问题，从而满足所有学生对于知识的需求。在提问题的时候还需要由浅入深，所有的知识点都必须环环相扣，促进学生主动探索意识的提升，并保障其相应的学习热情，实现教学的有效性。

例如，在教“弧长和扇形面积”这节内容的时候，对其弧长公式可以设计这样的一个情境：圆的周长公式大家还记得吗？然后学生回答“C=2πr”。教师继续提问，360°圆心角所对的弧长应该是多少？这时候学生就会开始思考起来。这时候教师再给学生一定引导，将其分为360等份，那么每一份的圆心角就是多少度？学生回答1°，那么就是将圆分为了360等份的弧。然后继续提问：1°的圆心角所对应的弧长是多少？4°的圆心角所对应的弧长是多少？那么根据这些问题就可以推算出来，最终弧长的公式为圆心角（圆周率）半径/180。

总的来说，在创设问题情境的时候必须以提升课堂教学效率为目的，同时还要因材施教，创设出科学合理的问题情境，进而优化学生的学习方式，进一步培养其创新能力和实践能力。

参考文献：

[1]翟玲.试论问题情境在初中数学课堂教学中的实践研究[J].师道·教研，2017（10）：81.

[2]方友正.巧设问题情境提升初中数学教学有效性[J].新课程导学，2017（20）：81.

作者简介：覃书逸（1978—），男，广西河池人，中学一级教师，本科，研究方向：初中数学教学。