串列三圆柱绕流的时均压力分布与气动力*

杨 群, 刘庆宽, 刘小兵

(1. 石家庄铁道大学土木工程学院 石家庄，050043)(2. 河北省风工程和风能利用工程技术创新中心 石家庄，050043) (3. 石家庄铁道大学风工程研究中心 石家庄，050043)

引 言

圆柱群结构广泛应用于实际工程。由于气动干扰的影响，圆柱群的气动力不同于单圆柱的气动力。由于布置形式简单，双圆柱的气动干扰问题受到了国内外学者的广泛关注[1]。与双圆柱相比，三圆柱绕流的研究文献相对少一些。文献[2-4]分别通过风洞试验对亚临界雷诺数下等边三角形布置三圆柱在不同风向角下的绕流进行了研究。结果发现，在小间距时，与单圆柱相比，三圆柱表面的压力分布有很大的改变。随着风向角的变化，会产生由邻近、剪切层和尾流3种不同机理引起的相互干扰效应。文献[5-6]对等边三角形布置三圆柱的绕流问题进行了数值计算，雷诺数分别为200和100。计算结果表明，较小间距时的干扰很严重，主要表现为邻近效应；较大间距时的干扰主要表现为尾流效应；中等间距时的干扰则表现为邻近效应与尾流效应的共同作用。Igarashi[7]研究了线形布置三圆柱在某一特定间距时的绕流特性，分析了三圆柱的压力分布、气动力及斯托罗哈数随风向角的变化规律。Liu等[8]通过风洞试验分别测试了均匀流场和格栅紊流场下串列三圆柱在不同间距时的气动力系数，并与串列双圆柱的气动力系数进行了对比。研究结果发现，两种流场下的气动力特性差异明显。与串列双圆柱类似，串列三圆柱的气动力也出现了临界间距现象。张力等[9]数值模拟了等间距并列三圆柱的绕流，雷诺数为100，两临近圆柱的中心距与单圆柱直径的比值T/D的变化范围为1.1～5.0。模拟结果发现，尾流模式与T/D密切相关，随着T/D的增大，会出现6种不同的尾流模式。

笔者通过风洞试验在亚临界雷诺数下对串列三圆柱在16个不同间距时的绕流进行了研究，详细分析了各圆柱的压力分布与气动力随间距的变化规律，并与单圆柱和串列双圆柱的压力分布与气动力进行了对比。限于篇幅，本研究主要讨论串列三圆柱绕流的时均压力分布与时均气动力。

1 风洞试验概况

图1 试验模型的尺寸及相对位置(单位：mm)Fig．1 Geometry parameters and relative location of test models (unit：mm)

图2 试验模型的测压孔布置Fig．2 Pressure tap arrangement of test model

采用有机玻璃圆管制作了3个外形一致，表面光滑的圆柱模型。如图1所示，模型的长度H=2 000 mm，横截面的直径D=80 mm。为保证模型在试验过程中不发生振动和变形，在每个模型的中间沿长度方向设置了刚性杆件。如图1和图2所示，在每个模型的中央位置截面等间距地布置了40个测压孔。为方便表示，采用圆周角θ来表示不同位置的测压孔。圆柱表面相对来流的最前端、最下端、最后端和最上端测压孔的圆周角θ分别为0°,90°,180°和270°。

为了与既有结果进行对比验证，首先进行单圆柱模型和不同间距串列双圆柱模型的绕流试验，然后进行不同间距串列三圆柱模型的绕流试验。如图1所示，对于串列双圆柱和串列三圆柱，相邻两圆柱的中心距L与单圆柱的直径D之比L/D分别为1.2,1.4,1.6,1.8,2.0,2.5,3.0,3.5,4.0,4.5,5.0,6.0,7.0,8.0,10.0和12.0。试验流场为均匀流场，背景湍流度小于0.4%。来流风速为6.4 m/s，以单圆柱直径D为特征尺寸定义的雷诺数为3.4×104，属于亚临界雷诺数范围。模型表面不同位置测压孔的风压通过电子压力扫描阀测得。电子压力扫描阀的采样频率为330 Hz，采样时间为30 s。

2 试验结果的可靠性验证

假设圆柱表面某测点处测得的瞬时压力信号的时间序列记为p(i)(i=Δt，2Δt，3Δt，…,NΔt)，其中：N为采样点数；Δt为采样间隔时间)。测点的压力系数定义为

(1)

其中:P∞为远前方来流的静压;U∞为远前方来流的速度；ρ为空气密度。

测点时均压力系数定义为

(2)

测点脉动压力系数定义为

(3)

圆柱的阻力系数和升力系数定义分别为

(4)

(5)

其中：FD(i)和FL(i)分别为各测点压力积分得到的圆柱单位长度上的阻力时程和升力时程。

圆柱的时均阻力系数和时均升力系数定义如下

(6)

(7)

图3给出了不同间距串列双圆柱的时均阻力系数，并与文献[10]的试验结果进行了对比。与本试验类似，文献[10]也是采用刚性模型测压风洞试验的方法来获得串列双圆柱的时均阻力系数。与本试验不同的是，文献[10]试验的雷诺数为2.0×104，双圆柱的中心距L与单圆柱直径D之比L/D的变化范围为1.25～6.00。从图4可以看到，本试验和文献[10]试验得到的串列双圆柱的时均阻力系数无论是具体的数值还是随L/D的变化规律均吻合较好。上下游圆柱的时均阻力系数在L/D=1.2左右时分别约为1.0和-0.5。在1.2≤L/D≤3.5时，随着L/D的增大，上游圆柱呈现出逐渐减小的变化规律，下游圆柱则呈现出先增大后减小的变化规律。在L/D=4.0时，上下游圆柱的时均阻力系数均发生了突升现象。上游圆柱的时均阻力系数由L/D=3.5时的0.75左右突升至1.10左右。下游圆柱的时均阻力系数由L/D=3.5时的-0.15左右突升至0.35左右。在4.0≤L/D≤6.0时，上下游圆柱的时均阻力系数随着L/D的增大变化不明显。以上对比分析验证了本试验结果的可靠性。

图3 本研究串列双圆柱的时均阻力系数与已有结果对比Fig．3 Compare of time averaged drag coefficient of present paper and existing paper for two circular cylinders in tandem arrangement

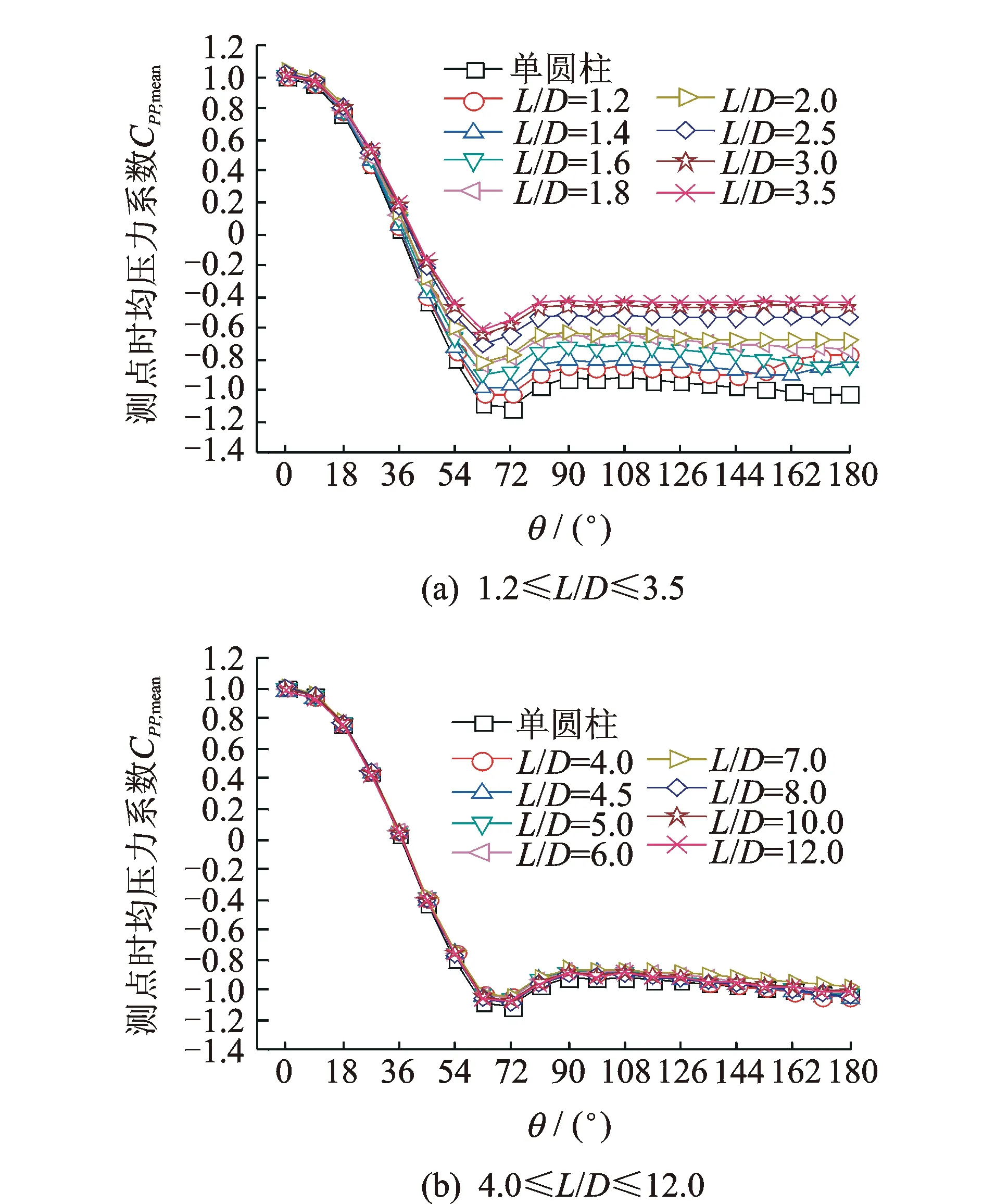
图4 单圆柱与串列上游圆柱各测点的时均压力系数Fig．4 Time averaged tap pressure coefficients of single circular cylinder and forward circular cylinder

图5 单圆柱与串列中游圆柱各测点的时均压力系数Fig．5 Time averaged tap pressure coefficients of single circular cylinder and middle circular cylinder

图6 单圆柱与串列下游圆柱各测点的时均压力系数Fig．6 Time averaged tap pressure coefficients of single circular cylinder and leeward circular cylinder

3 串列三圆柱的时均压力分布

图4～6分别显示了不同间距串列三圆柱的上游圆柱、中游圆柱和下游圆柱各测点的时均压力系数，各图中还给出了单圆柱对应测点的时均压力系数。由于压力分布具有对称性，各图中仅给出了圆周角θ在0～180°范围内各测点的时均压力系数。从图4～6可以清楚地看到，串列三圆柱的绕流存在两个完全不同的流态，两个流态切换的临界间距(L/D)cr为3.5～4.0之间。

从图4可以看到：a.当1.2≤L/D≤3.5时，上游圆柱与单圆柱时均压力系数分布的差异主要体现在60°≤θ≤300°的范围。在此范围内，上游圆柱的时均压力系数为负值，其分布曲线变得相对平坦，在θ=180°位置不再像单圆柱那样有明显的凹陷。随着L/D的增大，上游圆柱的时均负压系数绝对值呈现出逐渐减小的变化趋势。b.当4.0≤L/D≤12.0时，上游圆柱的时均压力系数基本不随L/D的变化而变化，且接近单圆柱的时均压力系数。

从图5,6可以看到，虽然中游圆柱与下游圆柱的时均压力系数具体数值有所差异，但是二者却有着相似的变化规律：a.当1.2≤L/D≤3.5时，两圆柱各位置测点的时均压力系数均为负值，且与单圆柱存在较大的差异。与中游圆柱相比，下游圆柱的时均压力系数更接近单圆柱的时均压力系数。两圆柱的前缘位置测点的负压系数绝对值随着L/D的增大均呈现出逐渐减小的变化规律。中游圆柱其他位置测点的负压系数随着L/D的增大变化不明显。下游圆柱其他位置测点的负压系数绝对值随着L/D的增大基本上呈现出逐渐增大的变化趋势。b.当4.0≤L/D≤12.0时，两圆柱前缘位置测点的时均压力系数基本为正值，且小于单圆柱前缘位置的时均压力系数，L/D越大，偏小幅度越小。两圆柱其他位置测点的时均压力系数为负值，其绝对值小于单圆柱对应位置的负压系数绝对值。测点位置不同，偏小幅度不同。L/D不同，偏小幅度基本不变。与中游圆柱相比，下游圆柱的偏小幅度更大一些。

4 串列三圆柱的时均阻力

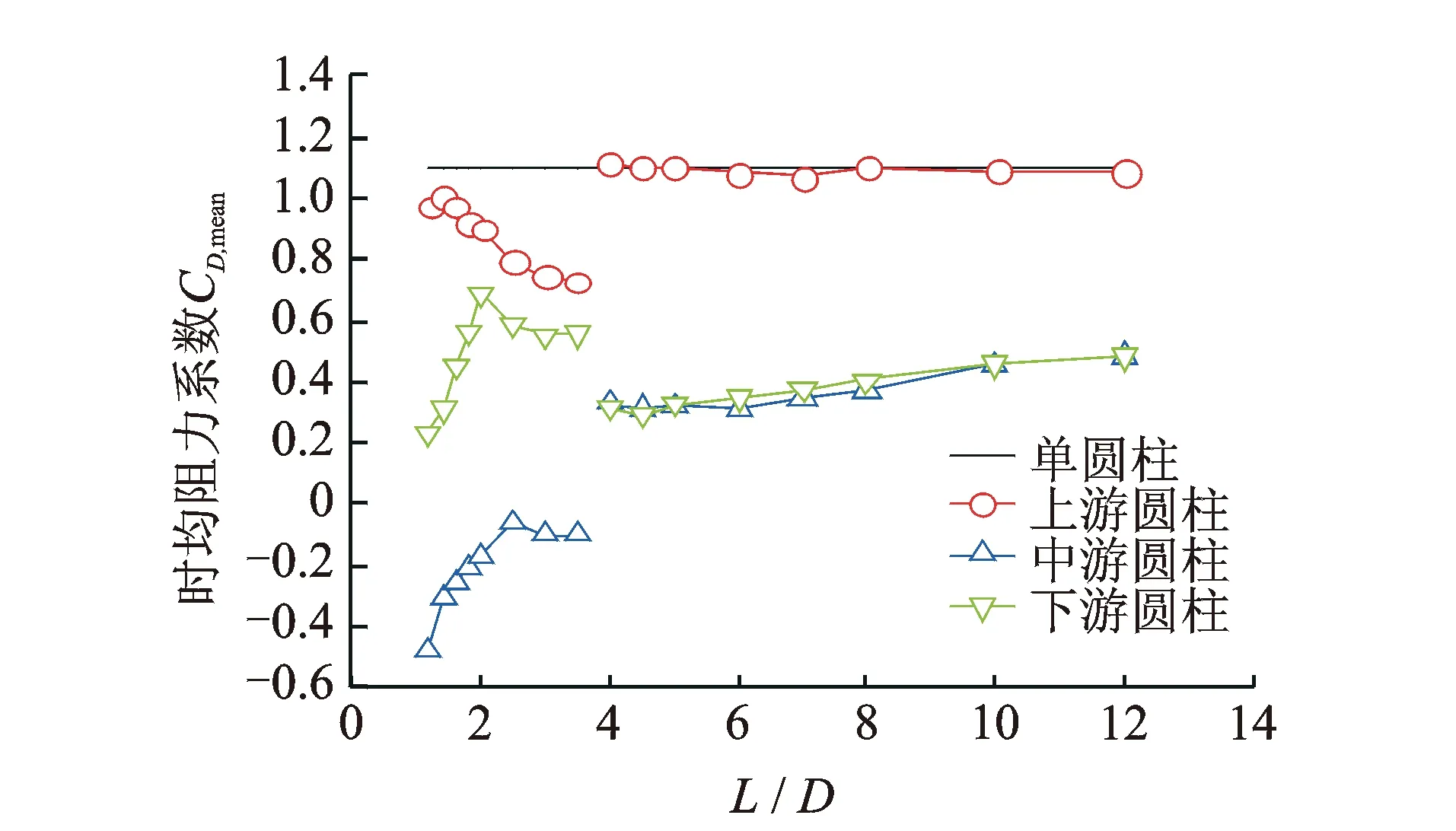
图7 单圆柱与串列三圆柱的时均阻力系数Fig．7 Time averaged drag coefficient of single circular cylinder and three circular cylinders in tandem arrangement

图7显示了串列三圆柱在不同间距下的时均阻力系数，并与单圆柱的时均阻力系数进行了对比。可以看到：a.当1.2≤L/D≤3.5时，上游圆柱的时均阻力系数随着L/D的增大而减小。中游圆柱和下游圆柱的时均阻力系数随着L/D的增大先增大后减小。3个圆柱的时均阻力系数均小于单圆柱的时均阻力系数。上游圆柱的偏小幅度最小，下游圆柱的偏小幅度次之，中游圆柱的偏小幅度最大。中游圆柱的时均阻力系数为负值，表明其受到了与来流方向相反的作用力。b.当L/D=4.0时，随着流态的切换，串列三圆柱的时均阻力系数发生了突变。上游圆柱和中游圆柱的时均阻力系数分别由L/D=3.5时的0.73和-0.10突升至1.11和0.33。下游圆柱的时均阻力系数由L/D为3.5时的0.55突降至0.31。随着L/D的继续增大，上游圆柱的时均阻力系数基本保持不变，且接近单圆柱的时均阻力系数。中游和下游圆柱的时均阻力系数非常接近，且小于单圆柱的时均阻力系数，偏小幅度随着L/D的增大缓慢变小。当L/D=12.0时，中游和下游圆柱的时均阻力系数分别为0.49和0.48，为单圆柱时均阻力系数的44%左右。

以上分析表明：当1.2≤L/D≤3.5时，气动干扰对串列三圆柱时均阻力的影响表现为减小效应，中游圆柱的减小效应最显著，下游圆柱的减小效应次之，上游圆柱的减小效应最不明显；当4.0≤L/D≤12.0时，气动干扰对上游圆柱时均阻力的影响可以忽略，对中游和下游圆柱时均阻力的影响程度相当，且表现为减小效应，这种减小效应随着L/D的增大缓慢减弱，即使当L/D=12.0时也不可忽略。

串列三圆柱时均阻力在临界间距附近的突变与流态的切换密切相关。当L/D=3.5时，从上游圆柱分离的剪切层由于中游和下游圆柱的挤压缺乏发展空间，没有在尾部形成旋涡脱落。上游圆柱和中游圆柱之间的流动很微弱，导致上游圆柱后缘的时均压力与中游圆柱前缘的时均压力非常接近，如图4(a)和5(a)所示。当L/D=4.0时，由于发展空间的变大，中游和下游圆柱的存在不再抑制上游圆柱的旋涡脱落，因此上游圆柱的后缘出现了非常强烈的负压，见图4(b)，而中游圆柱前缘的时均压力系数则由L/D=3.5时的-0.5左右突变为0值附近。以上时均压力的变化在整体上表现为临界间距前后上游和中游圆柱时均阻力的突升。对比图6(a)和图7(b)发现，下游圆柱时均阻力在临界间距前后变化的主要原因在于其后缘负压的变化。下游圆柱后缘的时均压力系数由L/D=3.5时的-0.8左右降低到L/D=4.0时的-0.4左右。这与L/D=4.0时下游圆柱尾部的旋涡脱落强度变弱有关。

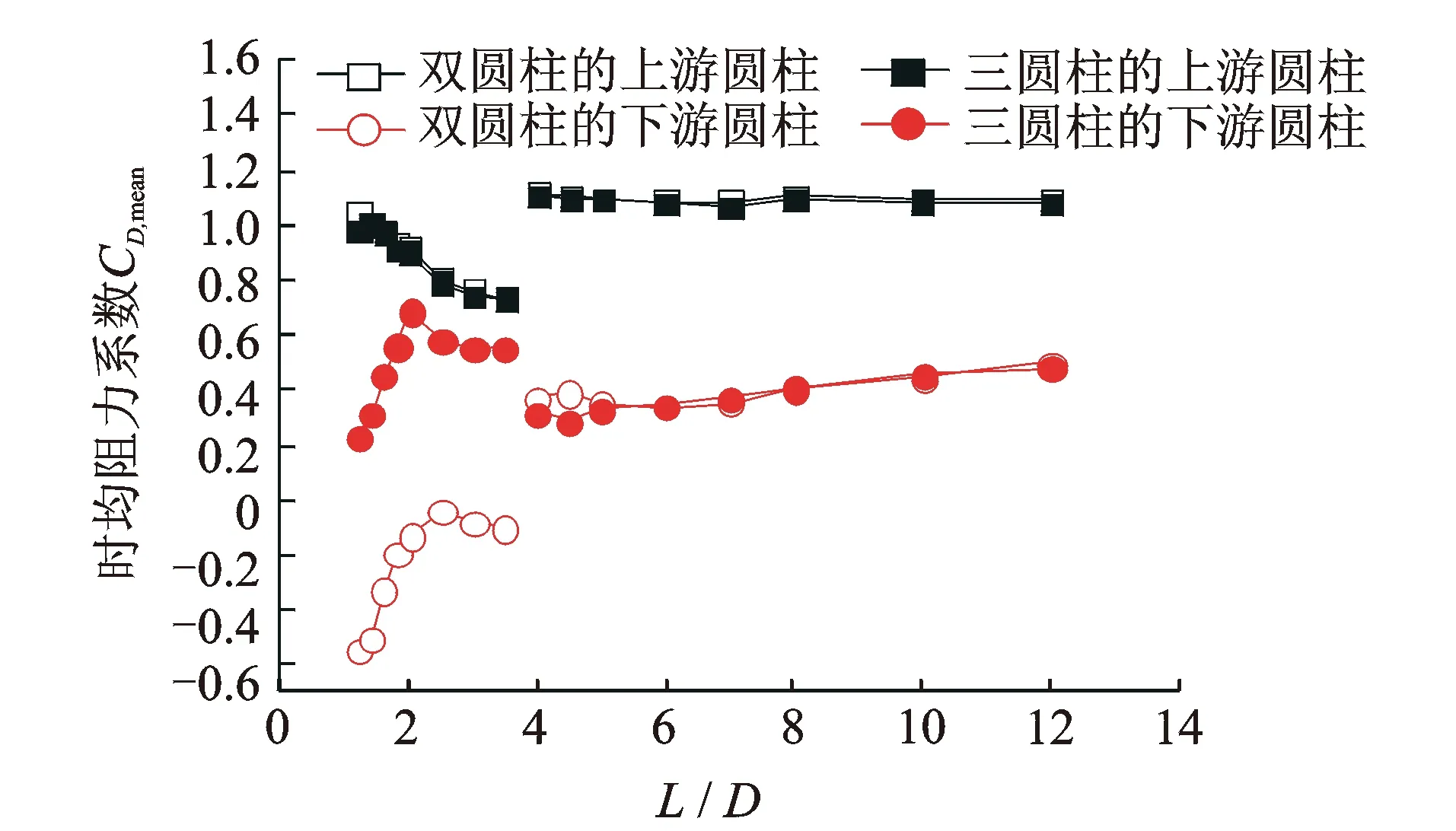
图8 串列三圆柱与串列双圆柱的上下游圆柱的时均阻力系数对比Fig．8 Compare of time averaged drag coefficient of forward and leeward circular cylinders for two and three circular cylinders in tandem arrangement

图8将串列三圆柱的上下游圆柱的时均阻力系数与串列双圆柱的上下游圆柱的时均阻力系数进行了对比。可以看到：a.两种布置方式的上游圆柱的时均阻力系数非常接近，这说明后方干扰圆柱增加对上游圆柱的时均阻力基本没有影响；b.两种布置方式的下游圆柱的时均阻力系数在L/D>(L/D)cr时基本接近，在L/D<(L/D)cr时差别较大，虽然均小于单圆柱的时均阻力系数，但串列三圆柱的下游圆柱的减小幅度更小。这说明前方干扰圆柱的增加对下游圆柱时均阻力的影响在L/D>(L/D)cr时基本可以忽略，在L/D<(L/D)cr时表现为减小效应的变弱。

5 结 论

1) 串列三圆柱的绕流存在两个完全不同的流态。两个流态切换的临界间距(L/D)cr为3.5～4.0之间。串列三圆柱在两个流态下的时均压力分布与时均阻力差异很大。

2) 当L/D<(L/D)cr时，气动干扰对串列三圆柱时均阻力的影响表现为减小效应，中游圆柱的减小效应最显著，下游圆柱的减小效应次之，上游圆柱的减小效应最不明显。当L/D>(L/D)cr时，气动干扰对上游圆柱时均阻力的影响可以忽略，对中游和下游圆柱时均阻力的影响程度相当，且表现为减小效应，这种减小效应随着L/D的增大缓慢减弱，即使当L/D=12.0时也不可忽略。

3) 增加后方干扰圆柱对上游圆柱的时均阻力基本没有影响。增加前方干扰圆柱对下游圆柱时均阻力的影响在L/D>(L/D)cr时基本可以忽略，在L/D<(L/D)cr时表现为减小效应的变弱。