借形助数，活化思维

江芝芬

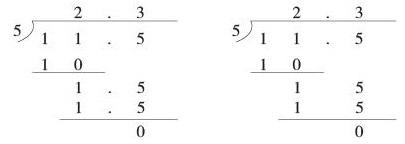
摘 要：借形助数，数及数量关系置于图形及生活的实物模型和现实背景中就能把数及数量关系化抽象为具体、化繁为简，还能发展学生的数感，促进学生理解知识并掌握知识，拓宽学生的思路，活化他们的思维，提升他们的探究兴趣与创造力，文章从四个方面进行阐述。

关键词：借形言数;思维;数感;数量关系;算式;数学语言

一、借形言数，发展数感

什么是数感？简而言之，就是人们对数与数之间关系的理解与感悟。如何发展学生的数感？若能借助图形、实物模型以及实际生活的素材等来丰富学生的感知，就能使抽象的数及数量关系形象化、具体化。

例如，在教学“十万的认识”这课时，十万对四年级学生来说是个较大的数目。如何引导学生通过已学的万以内的知识去类推、去感知，笔者通过小立方体及计数器两种直观模型并联系现实生活来帮助学生理解，发展他们的数感。我们知道这节课的难点就是接近整万数的数法，而数与数之间满十进一的计数单位间的变化对学生来说是较抽象的，为了让这个抽象的计数单位变得直观可见，我们就要引导学生把数数的思维方式“暴露”出来，让他们一万一万地数，并边数边观察小立方体的变化，在他们数到九万时，笔者有意稍作停顿，问学生“再添一万是多少”，让学生思考后自然而然说出“十万”，接着让他们与同桌合作，在计数器上边数边观察，计数器上珠子的变化及“十万”是怎么产生的？这样他们就在操作中直观地理解了“十万”与“万”的十进制关系。“十万的数目究竟有多大呢？”让学生带着问题与好奇到操场，借助熟悉的学校操场的跑道长度（400米）以及想象活动，让他们通过小组合作学习、探究，真切地感悟到生活中“十万”数目的大小：①十万毫米多长？②十万厘米多长？③十万千米多长？学生通过计算得知， 十万毫米等于100米，相当于跑道长度的1/4，十万毫米很短;十万厘米等于1000米，相当于操场跑道长度的2圈半，十万厘米有点长;十万千米相当于操场跑道长度的25万圈，相当于绕地球2.5圈的长度，学生惊叹：“十万千米真的好长呀！”通过结合生活中熟悉的操场的“形”来说“十万”这个数，学生直观地感受到“短、有点长、好长”，从中感悟“十万”这个数在不同的场景中给人的大小、多少的感觉是不一样的。如此，既能让学生印象深刻，发展数感，又能让学生拓宽思路，发展思维。

二、借形溯源，体悟知识

让学生亲身经历知识的产生、发展与形成过程，探清知识的来龙去脉，他们才容易理解与掌握，记忆深刻，從而真正实现有效教学。如在教学“用四舍五入法求小数的近似值”时，笔者听了一些老师的公开课均是直接告知学生“四舍五入法”“是用四舍五入法取小数近似数的时候，看它保留位数的后一位，如果后一位数的最高位数字≤4时，就把尾数去掉;若后一位数的最高位数字≥5时，就把尾数舍去并在保留的这位数上进“1”，然后学生熟记方法，再强化应用，他们认为这是约定俗成的所以就直接告知。课后我问学生“你知道为什么尾数的最高位数≥5，就把尾数舍去并在保留的这位数上进‘1;尾数的最高位数字≤4，就把尾数直接舍去？”学生异口同声地答道：“老师说这是规定的。”

如何让学生“知其然又知其所以然”呢？笔者在自己的班级里做了尝试，以一位小数为例：把0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9在下面的线段图中找出来，并说说它们更接近0还是1？

学生结合线段图很快就明白大于0.5的数更接近1，小于0.5的数更接近0，而居中的0.5人们就把它归为接近1。因此，规定在取近似值时，看保留位数的下一位，如果是0～4的5个数字就直接把尾数舍去，如果是5～9的5个数字就在保留的这位数上加1后再把尾数舍去，这样就刚好5个数字的尾数是舍去，5个数字是进“1”后舍去，这种保留法的误差总和是最小的。所以，为了便于计算，人们就使用四舍五入法。通过在直观的线段图上找数，并结合线段图说清哪些数更接近1与0，学生很容易就理解了“四舍五入”的道理，且在提升其探究能力的同时，使模糊的知识明晰化。

三、借形明理，厘清关系

（一）厘清计算之理

算理是内隐的、抽象的，是计算之根，只有厘清算理才能使计算之树枝繁叶茂。那如何让抽象的算理变得清晰可见？何时“借形助数”方有效？教师在厘清教材的编写意图，了解学生的知识“盲点”后，应创造性地使用教材，灵活地选择有效的“形”。如在教学“小数除以整数”时，笔者放手让学生探究11.5÷5的竖式计算，出现了以下两种算竖式：

我引导学生认真观察，并组织辩论：竖式中的部分积究竟写15还是1.5呢？刚开始绝大多数学生都认为应写1.5，极少部分学生认为是15，至于为什么是15却讲不清楚，这时笔者给他们出示了计数器引导他们借助计数器来说说“你是怎么把11.5平均分成5份的？”借助直观形象的计数器，学生明白了从高位除起，高位上的数不够除，就把它转化成较低位上的数和较低位上的数合起来继续除，个位上11个珠子平均分成5份后还余1，个位上1要化成10个0.1，再和十分位的5个0.1合成15个0.1，15个0.1再继续平均分成5份，说到这里，学生恍然大悟：“应该是写15不写1.5，因为……”学生的顿悟源于他们熟知的计数器这个直观形象模型的启发，借助这个模型学生的思路清晰，学习效率不言而喻，且对后继研究除数是小数的除法的算理铺路搭桥。

（二）厘清数量关系之理

正确分析数量关系是解决数学问题的关键。为促进学生有效分析数量关系、厘清解题思路，帮助学生思考，应引导学生动手画画线段图、简易分析图或想象实物模型等，借助直观形象的“形”把复杂的问题变得简明、形象、易于思考。为提升学生探究兴趣，促进学生思考，拓展学生思维，笔者在新知教学后经常会让学生进行“思维操练”。如学生刚学完假分数时，笔者出示：“如果一个分数分子与分母的和是30，分子加4且分母不变。则这个分数值是1。原来的分数是多少？”刚开始很多学生不知所措，紧皱眉头，不知如何解答，我提醒他们：“当遇到不好解决的问题时，我们经常是怎么解决的？”学生说：“画线段图或举例。”我说：“那就动动手，用线段表示分子、分母，看看会不会有启发。”学生独立思考，然后和同桌交流，相互补充，画出了以下线图：

这时，很多学生惊喜地说：“老师，我明白了！”“你明白了什么？”有的学生迫不及待地跑到黑板前指着线段图说：“先画一条线段表示分子，现在分子加4，分数值是1，什么意思呢？因为分子分母相等的分数是1，那分子加上4这段就和分母这段一样长了。把原来分子分母的和30加上4等于34。它就是分母的2倍，把34除以2得到17，17就是原来的分母，把分母17减4得13就是原来的分子，所以原来分数是十七分之十三。”

通过简易的线段图把看似复杂的数量关系理得条分缕析，学生的思维从不知所措的迷茫到“柳暗花明”時的惊喜皆源于直观形象的线段图。

四、借形解式，化繁为简

很多复杂的算式，如果按四则运算法则计算，难而且繁杂，且容易出错，若能善用图形，巧用图形，就能将复杂的算式巧妙地转化为很简单的式子，而且使算式变得具体形象，更能激发学生的探究欲望。学完通分后，我出示了一道拓展题。如++ +，由于受思维的定势作用，学生看到题目纷纷作答，大部分学生用通分的方法计算，少部分学生化成小数计算，我问：“还有其他方法吗？”学生默然，于是笔者出示 ，启发学生思考：“答案就藏在这个长方形里，看谁的眼睛最亮？”很多学生半信半疑，笔者又接着说：“你能把这个算式中的分数在这个长方形中找出来吗？”一石激起千层浪，学生们有的动手画，有的与同桌一起讨论，最终有学生得出下面的线段图：

此时，有学生兴奋地喊道：“1- = 。”然后笔者让他们结合图形讲清道理。之后，又让学生在算式后增加了 +，让他们观察、计算，并说说有什么发现。掌握了方法后，他们说：“老师，照这样规律不管再增加几个分数，结果都是用‘1减最后一个分数”“那最后结果会等于1吗？”“只能无限接近1，不可能等于1”……学生们都惊叹：“图形真的很神奇！居然能帮我们把这么复杂的算式变得这么简单易懂。”

其实，在数与代数领域，图形的功用远远不止这些，诸如数的大小比较、运算定律的解释、问题解决等，都可以借助图形或实物模型来引导学生进行思考，能够让学生在理解与掌握知识、提升学习力的同时，提升学习数学的素养，让数学知识变得更有生命力与魅力。

参考文献：

[1]陈红霞.以形助数，化难为易——试谈数形结合思想在小学数学教学中的应用[J].湖北教育（教育教学版），2010（3）：17-18.

[2]毕娉婷.数学教学中数形结合思想的应用分析[J].教育现代化，2017（15）：134-135.