变教材“要求”为学生“需求”
——“整数除以分数”教学实践与思考
2019-11-05程进生
程进生
“分数除法”是苏教版六年级上册的内容。其教学分成三个层次,分别是分数除以整数、整数除以分数和一个数除以分数,螺旋上升。“整数除以分数”有承上启下的作用。
一、课前思考
与人教版对比,两者推导“整数除以分数”计算方法的思路不同。人教版(六上第31页)通过抽象“推理”出计算方法,如例2中解决“小明小时走了2km,小明平均每小时走多少km”这个问题,教材是这样说明的,即“先求小时走的千米数,也就是求2的即再求3个小时走的千米数,即进而整理得出推理过程较为抽象,有“教了也不懂(为什么乘除数的倒数),不如不教”的尴尬。苏教版(六上第44、45页)为避免类似的尴尬,强调了直观化,借助直观形式“看出”计算方法,例2中先画图分橙子写结果,接着就出现“从上面的结果可以看出从上面的结果可以看出的结语,这是拿形式说方法,并未深入到算理的实质。
如果对算理理解都有困难,学生还能自己探索出教材中呈现的推导方法吗?笔者以为,实际教学中,不妨给学生一个开放的空间,让其自由地思考、自主地探索计算方法,变教材的“要求”为学生探索的“需求”,而不只是囿于教材中出现的唯一推导方法。
为了发现学生探索时的着“火”点,笔者进行了学情前测。前测题目:4个同样大的橙子分给小朋友。①如果每人分个,可以分给几人?②如果每人分个,可以分给几人?③每人分个呢?把你的想法表达出来。
前测(45人参与)结果是:九成多的学生能得出问题①②的正确结果,能得出问题③的结果的人数不足三成。解题方法各异,其中画图法运用得最多,把分数转化成小数直接计算的次之,运用商不变规律计算的有3人,而用“颠倒除数相乘”直接计算的有5人。访谈后得知,“颠倒除数相乘”法,有的是自己看书知道的,有的是父母告诉的,至于原因说不明白。
从调查中知道,学生对整数除以分数并不是一无所知,他们有自己的思考和想法,直观模型是多数学生的“脚手架”,“联系转化”可以成为抽象推理教学的突破口。于是变教材“要求”为学生“需求”的教学路径清晰了。
二、教学实践
(一)展示作品,顺应学生思维“需求”
【教学片段呈现】
师:同学们课前已经解决过了,老师现在把你们当中的一些想法展示出来(如图1)。
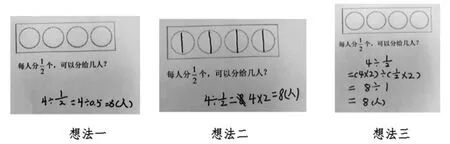
图1
师:为什么用除法来列式?
师:对,“求一个数里有几个另一个数”用除法计算,这个除数可以是整数,也可以是分数。分数除法和整数除法的意义是相通的。
师:观察一下这三种做法,你看明白了哪种?(留足时间给学生思考)
师:这是个不错的策略,把分数除法转化成小数来计算,对这个策略你们有什么疑问?
师:这是个问题,说明转化成小数去计算有它的局限性。
生:第二种方法是用画图来想到的。通过看图,我们知道每个橙子能分给两个人,所以4个橙子就能分给4×2个小朋友。
生:第三种方法,是把分数转化成了我们学过的整数来除的,这有点像我们学习小数除法时用到的策略——把除数是小数的转化成除数是整数的来计算。
师:是运用了什么规律来把分数除数转化成整数来计算的呢?
生:被除数和除数同时乘2。哦,对了,是商不变的规律。
师:这里是同时乘2,那么同时乘3或同时乘其他整数可以吗?
生:同时乘2除数就变成了1,如果同时乘3,除数还是分数,如果同时乘4也行,除数也是变成了整数2,也能算出来。
师:那么同时乘哪个数计算时会更简单呢?
生:同时乘2更简单,因为除数乘2后变成1,当然计算会更简单。
【思考】“平均分东西”的情境帮助学生沟通了分数除法和整数除法的意义。展示来自不同学生的解题策略,既满足了他们的表现欲,更让不同水平的学生在数学思考中都有所收获。在多样化的算法中,有直观计算的“合情”,也有抽象运算的“合理”,体现了学生的“转化”思想。由学生的本真思维切入教学,效果较为理想。
(二)放手迁移,顺应经验内化,提升“需求”
【教学片段呈现】
师:课前没有思考出来的同学,现在再做做看。
生:我用了两种方法,第一种是画图法,一眼就可看出分成了12份,也就是每个橙子可以分成3份,所以4×3=12(教师顺势板书式子)。第二种是把被除数和除数都同时乘以3,变成12÷1=12。(如图2)

图2
生:这道题不能把分数转化成小数来计算了。第二种把除数转变为1,好简单!好像所有的分数除数都可以变为1。
师:对,那分数除数怎么能变为1呢?
生:乘积是1的两个分数互为倒数,所以只要乘除数的倒数就行了。我知道前面我们为什么要学习倒数了!
师:你的想法很有意义。我们可以利用商不变的规律,把分数除数变成1再除,除数变成1只要乘它的倒数就可以了。
师:用商不变的规律去计算一下,再用画图进行验证,看看结果对不对?
教师展示学生的画图验证(如图3)。
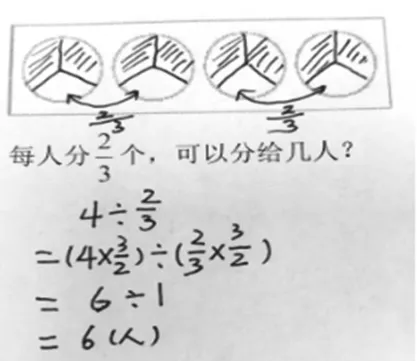
图3
师:画图的验证结果和我们用商不变规律计算的结果是一样的。
师:同学们观察一下黑板上的几个算式(见图4),它们的除数都变成了1,因此除得的结果只要看被除数怎样变化就可以了。老师把除数这一部分变化过程擦去,你们再观察、对比一下每个算式的前后变化,你有什么想说的?
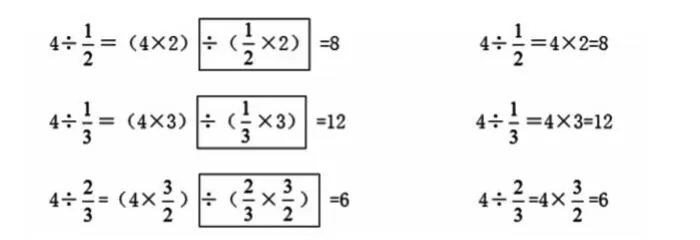
图4
生:被除数和除数同时乘除数的倒数,只要用被除数乘除数的倒数就可以了,因为这时候除数已经变成了1,而任何数除以1都等于它本身,除数1可以省略不写。
生:对,计算分数除法不需要同时乘倒数,可以省略一步,只需要把被除数乘除数的倒数就行了。
师:重要的话说三遍,谁还愿意再说三遍?(同桌互相说,师板书:整数除以分数,等于整数乘这个分数的倒数)
师:我们探讨了分数除法——整数除以分数,我们利用“商不变规律”进行了转化,这不仅适用于我们学过的整数、小数除法,也同样适用于今天学习的分数除法。在利用“商不变的规律”的过程中,我们通过优化算式,使分数除法转化成分数乘法,计算变得简单。可见,很多知识都是相通的!
【思考】放手让学生充分利用上一个环节中获得的计算经验,自主探索除数是和的除法。亲历了转化的过程,学生知道把分数转化成小数计算的局限性,意识到除数转化为“1”是一个好办法,并在此基础上通过观察、归纳等活动,逐渐明白“除以一个分数,等于乘这个分数的倒数”的方法实际上是应用商不变规律的优化形式。如此,学生不仅体会到数学知识之间的联系,而且能积累探索计算方法的经验,发展数学思维能力。
(三)引导联想,看学生思维拓展“需求”
【教学片段呈现】
师:通过今天的学习,你还有哪些疑问?
生:把除法转变为乘法来计算,我还是第一次见到,算是开了眼界了。那小数除法能不能转化成乘法来计算?
师:这是个不错的问题!课后几个人在一起研究研究,如果能转化为乘法来计算,方法简捷吗?
生:分数除法除了“颠倒除数相乘”这个方法外,还有没有其他的算法?
师:“颠倒除数相乘”这个说法很好,也很简洁!人们在解决一个问题时,往往能想出很多办法,分数除法的方法也有多种。在我国古代,还有在古巴比伦等国,都出现过其他的算法,有兴趣的同学可以在课下搜索。随着历史的发展,人们最终都喜欢用“颠倒除数相乘”法,因为它简单易行!
【思考】对算理的真实理解,激起了学生的联想,使学生把学习的触角延伸到数学研究的深处,拓展至“分数除法计算”的发展史。教师的“因为它简单易行”,让学生初步明白:计算方法虽不唯一,但“颠倒除数相乘”的计算法则是数学概括性和简洁性的选择,也是提高运算效率的必然选择。
三、课后反思
本节课的教学,用直观形式和抽象推理互为表征、相辅相成,有利于学生对算理的理解,提高了思维的含金量。变教材“要求”为学生“需求”是本节课取得较好效果的关键。
(一)突破教材,让学生“自嗨”
教材是通过直观模型来帮助学生理解算理的。但很多学生并没有如教材所要求的明白算理,只是被动接受算法。教材的要求与学生的“最近发展区”往往是有偏差的,故在教学中,不如放手让学生先“自嗨”,教师见机了解学情。奥苏伯尔曾说过:“影响学习的最重要因素是学生已经知道了什么,我们应当根据学生的已有知识状况进行教学。”因此基于学情而突破教材的课就未必不是好课。
(二)寻找有故事的作品,调控学生的“自嗨”
在学生“自嗨”探索解决问题时,他们已不是坐着板凳看课本剧的“吃瓜群众”,他们会积极地投入进去,调动以往经验,努力思考问题解决的办法。前测作业纸里,虽没有出现与教材里一致的“规定”范式,但多数解题的背后,是有故事的,都蕴含着一个合情或合理的算理。从画图到转化成小数计算,再到运用商不变规律,教师只是顺应学生本真的思维适时“点火”,恰当调控。
(三)依照作品算理,建立知识间的联系
学生“自嗨”的作品中,看似“法”不同,但“理”是关联的。由于学生涉“知”不深,教师需要引导他们比照各“法”,帮助建立知识间的联系,使学生清晰地感受到“转化”策略的魅力,深刻理解“商不变规律”的适用性,达到真正意义上的理解。
