解题中的替换推理

郜舒竹

“替换（Substitution）”是人们经常性开展的活动，比如物品的以旧换新，是将旧物用新物替换。再比如购物，是用所需物品替换货币，使得物品出现或增加，货币消失或减少。数学解题过程中，替换也是经常使用的做法，挖掘其背后的想法，使得替换成为一种推理形式，对于提高解题教学的质量十分有益。

一、什么是替换推理

“替换”指的是人的一种行为或做法，将原有对象改变为一个新的对象，在数学中也叫作“代换”。比如对于一般的圆面积公式πr2，此时半径是用一般的字母r表示，表达的是任意一个圆的半径与面积都具有这样的关系。如果已知一个特殊的圆半径为5厘米，为了求出这个圆的面积，就需要将公式中的r，替换为具体的数字“5”，圆面积公式就成为“52π”。其中出现了用数字“5”替换字母“r”的做法。

替换的做法，在数学解题中应用极其广泛。①注释：比如对于不定积分∫2xsin(x2)dx的计算，就需要用新变量u替换x2，将不定积分∫2xsin(x2)dx变为∫sinudu。其特点是替换对象与被替换对象具有某种“守恒（Conservation）”的关系，也就是形式上发生了变化，甚至因变化所导致的差异很大，但某种数量或性质是不变的，或者是有规律地变化的。比如用分数替换虽然形式上二者不同，但分数值是相同的。替换作为一种做法，其中必然隐藏着人的想法，这样的想法往往反映为对如下问题的思考：

● 谁需要被替换？

● 谁来替换？

● 为什么能够替换？

● 为何替换？

● 替换后什么变了？什么没变？等等。

对这些问题的思考，自然就会出现从判断到判断的推理，也就使得替换过程成为了思维的推理过程。不妨把这样的推理过程叫作“替换推理（Substitutive Reasoning）”。替换推理不仅在针对算式的计算中应用广泛，而且在许多问题的解决中也有效。

二、替换中的守恒

20世纪美国数学家、航海家，纽约州汉密尔顿学院教授，查尔斯·斯坦利·奥吉尔威(Charles Stanley Ogilvy：1913—2000)，在其所著《数学之旅（Excursions in Mathematics）》中，曾提出一个著名的红酒问题：

两个大小、形状完全相同的杯子A和B，A中有半杯红酒，B中有半杯水，二者容量相同。如果将A杯中少量红酒倒入B杯水中搅匀，此时B杯中就成为红酒与水的混合溶液。再将B杯中同样多的溶液倒回A杯。这时两杯都成为红酒和水的混合溶液，而且容量相同。也就是A杯红酒中有水，B杯水中有酒。那么A杯酒中的水，与B杯水中的酒，哪一个更多？[1]

有观点认为此时B杯水中的酒，要比A杯酒中的水多，因为第一次从A杯倒入B杯是纯酒，而第二次倒回时是酒和水的混合溶液。①致谢：2019年9月21日，在日本创价大学教育学院的国际高峰论坛后的酒会中，本题出示给与会学者以及创价大学学生，引起极大兴趣和热烈讨论。许多观点源于这次轻松、愉悦的讨论。特别感谢创价大学教育学部学部长铃木将史教授所给出的深入浅出的解释。

其实如果运用替换推理，很自然可以想到，B杯水中的酒与A杯酒中的水，实质是相互替换的关系。水中的酒与酒中的水相互替换，二者自然应当是相同的（见图1）。

图1 酒、水替换示意图

图1中左图下边白色部分表示A杯酒中的水，右图上边阴影部分表示B杯水中的酒。二者容量应当是相同的。可以用具体数据的计算验证这个结论。假定开始两杯中各自的红酒和水容量分别为2升，第一次将A杯中1升酒倒入B杯，那么B杯溶液中红酒与水的关系为1∶2。

替换是为了变化，而变化过程中往往存在着不变，能够识别这种变化过程中不变的因素，在数学与科学问题的思考中，叫作“守恒（Conservation）”。事实上，也就是发现规律的能力，是解题教学中需要特别关注的内容。

三、替换中的变化

替换过程中不仅要关注守恒，也要关注替换所引起的协同变化及其规律。比如对于鸡兔同笼问题：假设共有35个头，94只脚，求鸡和兔各有多少只？这一问题的解法很多[2]，诸多做法可以总结为表1中的八种。

表1 鸡兔同笼问题解法列举

根据表中所列出的八种第一步做法和想法，都可以推理出问题答案。所有做法都会运用到鸡和兔相互替换的思考过程。

以表1中序号8做法“35÷2=17.5”为例，这时头脑中出现了不符合实际的虚拟情境（Non-real Context），鸡和兔各有17.5只。虚拟情境下鸡和兔的总脚数为：(4+2)× 17.5=105（只），比实际脚数94多出了105-94=11（只），之所以多出11只脚，说明虚拟情境中的兔只数比实际多了，此时就需要将若干只兔替换为鸡，使得鸡只数增加，兔只数减少。每一只兔替换为一只鸡，头数不变（守恒），脚数发生了变化，减少2（见图2）。

图2 鸡替换兔示意图

一共需要减少11只脚，因此用鸡替换兔的只数为：11÷2=5.5（只）。也就是在虚拟情境中，应当用5.5只鸡替换5.5只兔，使得鸡只数增加5.5只，兔只数减少5.5只。得到实际情境中鸡只数为17.5+5.5=23（只），兔只数为17.5-5.5=12（只）。

这一推理过程可以概括为，通过对总头数取半（Halving）得到虚拟情境，而后通过鸡和兔相互替换，将虚拟情境转变为真实情境。替换过程中的关键是在头数守恒的基础上，把握脚数的变化规律。

四、思维中的替换

美国20世纪著名的数学游戏大师马丁·加德纳（Martin Gardner，1914—2010），曾经发表过一个行车过程中的“速度问题”：

某人驾车从A地去B地办事，计划全程平均速度为每小时60千米，可以按时赶到。因为路况问题，行驶至半途时发现，前半程行驶速度只有每小时30千米。为了按时赶到，他决定后半程加速行驶。那么后半程速度为多少时，才能使得全程平均速度为每小时60千米？[3]

在这一问题的思考中容易出现的一个误解，是运用“盈亏互补”的想法，因为前半程每小时30千米，比计划速度每小时60千米减少了30千米，因此后半程速度就需要在60的基础上增加30，使得速度为每小时90千米，就可以按时赶到。

如果运用平均速度等于“总距离÷总时间”进行检验，可以发现这个结论并不正确。假设全程距离为“1”，那么前半程和后半程距离分别为0.5，所用时间分别为小时和小时。全程平均速度为：

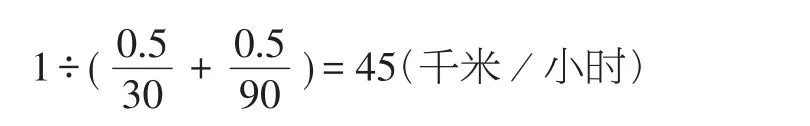
结果并不等于60。事实上，如果采用替换推理，将速度这个思考对象替换为时间，问题就会变得异常简单。

如果把问题稍微改变一下：前半程速度的每小时30千米，改变为每小时50千米。那么后半程提速到多少，能够按时赶到？

可以采用与前面类似的推理过程，将针对速度的思考，替换为对时间的思考。前半程速度为每小时50千米，是计划速度每小时60千米的那么前半程实际所用时间是计划时间的也就是倍，占用了后半程的时间。因此后半程时间只能是计划时间的运用速度与时间的反比例关系，立刻知道后半程速度应当是计划速度的倍，能够使得全程平均速度为每小时60千米，因此后半程速度应当是60的倍，即每小时千米。

这样思维对象的替换，实质是利用两个量之间的协变关系，将针对一个量的思考，替换为针对另一个量的思考。前面问题中就是将针对速度的思考，替换为针对时间的思考。

五、错误的替换

值得注意的是，任何替换的做法都是有条件的。在某条件下可行并且有效的替换，在另外的条件下可能是不可行或者无效的。

如果想将分数基本性质继承到指数运算中，就需要增加新的条件。再比如，对于长度的度量有下面的关系：

● 1米等于10分米

● 1分米等于10厘米

● 1米等于100厘米

不当的替换，会出现错误的结论：

这个推理过程，表面看每一步的计算都是正确的，得到的是“1米=1厘米”的悖论，原因是将“100厘米”替换为“10厘米×10厘米”是不可行的。100厘米表示一维线性的长度，可以写为“10×10厘米”，即1米等于10厘米的10倍。而“10厘米×10厘米”表示二维平面的面积，意义是“100平方厘米”或“0.01平方米”。因此“10×10厘米”与“10厘米 ×10厘米”本质上是不一样的，不具备守恒的关系。类似的错误替换还可以得到“1百元=1元”的悖论：

综上，替换作为数学解题中常用的做法，其中蕴含着的守恒、变化规律以及可行性等诸多想法，使其成为一种思维中的推理形式。教学中让学生有机会经历这样的推理，无疑对于彰显解题的育人功能会有所裨益。