步枪弹对带软硬复合防护明胶靶标的侵彻机制研究

韩瑞国，金永喜，卢海涛，王舒，王建中

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081；2.中国兵器工业第208研究所 瞬态冲击技术重点实验室，北京 102202)

0 引言

现代战争中，各国普遍为士兵配备防护装备以防御枪弹、高速破片等投射物的威胁。根据构成防护装备的材料性质可以将单兵防护装备分为软防护、硬防护以及软硬复合防护，其中由陶瓷复合插板和软防护组成的软硬复合防护主要用于防御高速步枪弹的威胁。软硬复合防护中陶瓷复合插板的主要作用是使弹体破碎、镦粗变形从而消耗弹头能量，而软防护则使弹头的撞击能量分布到更大的作用范围内，减轻对有生目标的伤害。尽管软硬复合防护能够有效阻止步枪弹的穿透，但高速冲击过程中通过防护传递的能量仍会对防护后的有生目标造成钝性损伤，严重时会致人重伤或死亡[1-2]。开展步枪弹对软硬复合防护下模拟靶标的非穿透性钝性损伤机制研究，对防弹衣结构改进设计、枪弹结构优化以及防护后钝性损伤的诊断治疗具有一定的指导作用。

弹道明胶(质量分数10%、温度4 ℃)是一种浅黄色透明介质，与有生目标的肌肉具有相似的力学性能，能够采用高速摄影记录靶标的动态响应，同时具有性能稳定、试验数据一致性好、便于埋设测试设备(如压力传感器)等优点，因此常用于模拟有生目标的肌肉组织[3]。目前，考虑到有生目标机体的特殊性和结构的复杂性、试验操作简易程度以及数据一致性等因素的影响，国内外普遍采用带防护的明胶靶标来开展防护后钝性损伤研究[3-6]。Cronin等[7]对明胶内的压力波双峰值现象进行了数值模拟，并分析了在Kevlar防弹衣防护下肋骨受到钝性冲击的动态响应。Roberts等[8-9]构建了手枪弹侵彻带软防护人体躯干的有限元模型，徐诚等[10]和Ma等[11]建立了步枪弹侵彻带软硬复合防护人体胸廓模拟靶标的有限元模型，分别对手枪弹与步枪弹非穿透防护时人体上躯干靶标的动态响应过程进行了数值模拟，模拟结果的各参数量级与试验结果相当。Wen等[12]研究了7.62 mm步枪弹侵彻软硬复合防护下明胶靶标的瞬态响应过程，数值模拟结果与试验结果的大小和变化趋势一致；罗少敏等[13]和Luo等[14-15]研究了手枪弹和步枪弹非贯穿作用下防护后明胶靶内的瞬态响应，获得了防护后明胶靶标内峰值压力和空腔膨胀的响应特征。Rafaels等[16]采用人体胸廓模拟靶标和数字图像相关方法，对枪弹撞击软质和硬质防护的背面动态变形行为进行了试验研究，确定了软质和硬质防护产生相似背面变形的弹道条件。孙非等[17]模拟了7.62 mm手枪弹作用下软质防弹衣后明胶靶标的动态响应，分析了手枪弹非穿透钝击作用力学机理。唐刘建等[18-19]研究了手枪弹冲击软防护下人体上躯干模拟靶标的防护变形和典型器官处的动态压力响应规律。然而目前的研究工作并未全面阐明步枪弹对防护后明胶靶标的钝性作用机制，尤其是多种动力学响应的定量关系。基于此，本文采用数值模拟与试验验证相结合的方法，深入研究了某步枪弹对带软硬复合防护明胶靶标的非穿透性侵彻作用过程，建立了数值模拟模型，计算获得了弹- 靶相互作用过程中多种力学响应的定量关系，为防护后钝性损伤机制研究、枪弹结构改进以及单兵防护结构设计优化提供了参考。

1 数值模型与试验验证

1.1 研究对象

本文研究了某步枪弹对带软硬复合防护明胶靶标的高速撞击过程，该步枪弹由覆铜钢弹头壳、铅套和钢芯组成，如图1(a)所示。试验中弹头撞击靶标的速度为(880±8)m/s，入射角度接近0°，因而在数值模拟模型中设定弹头着靶的速度为880 m/s，入射角度为0°. 模拟靶标由陶瓷复合插板、超高分子量聚乙烯(UHMWPE)软防护和明胶靶标组成，如图1(b)所示，其中陶瓷复合插板由厚度为7 mm的99.5%Al2O3陶瓷和厚度为11 mm的UHMWPE背板组成，整体尺寸为300 mm×250 mm×18 mm；软防护由46层UHMWPE无纬布按0°和90°的方向正交重叠构成，总厚度为9.2 mm，整体尺寸为300 mm×300 mm×9.2 mm. 明胶靶标采用质量分数10%、温度4 ℃的明胶，尺寸为300 mm×300 mm×300 mm.

图1 步枪弹示意图与带软硬复合防护的明胶靶标Fig.1 Rifle bullet and gelatin target with soft/rigid composite armor

1.2 有限元模型

1.2.1 步枪弹有限元模型

在有限元分析软件ANSYS前处理模块中，采用8节点六面体实体单元Solid164划分步枪弹的网格，其中，弹头壳圆弧部划分为8段，圆弧部与圆柱部交界面处由3个单元过渡为2个单元；细化钢芯前端的网格，网格尺寸大小从头部向尾部逐渐增大，如图2所示。

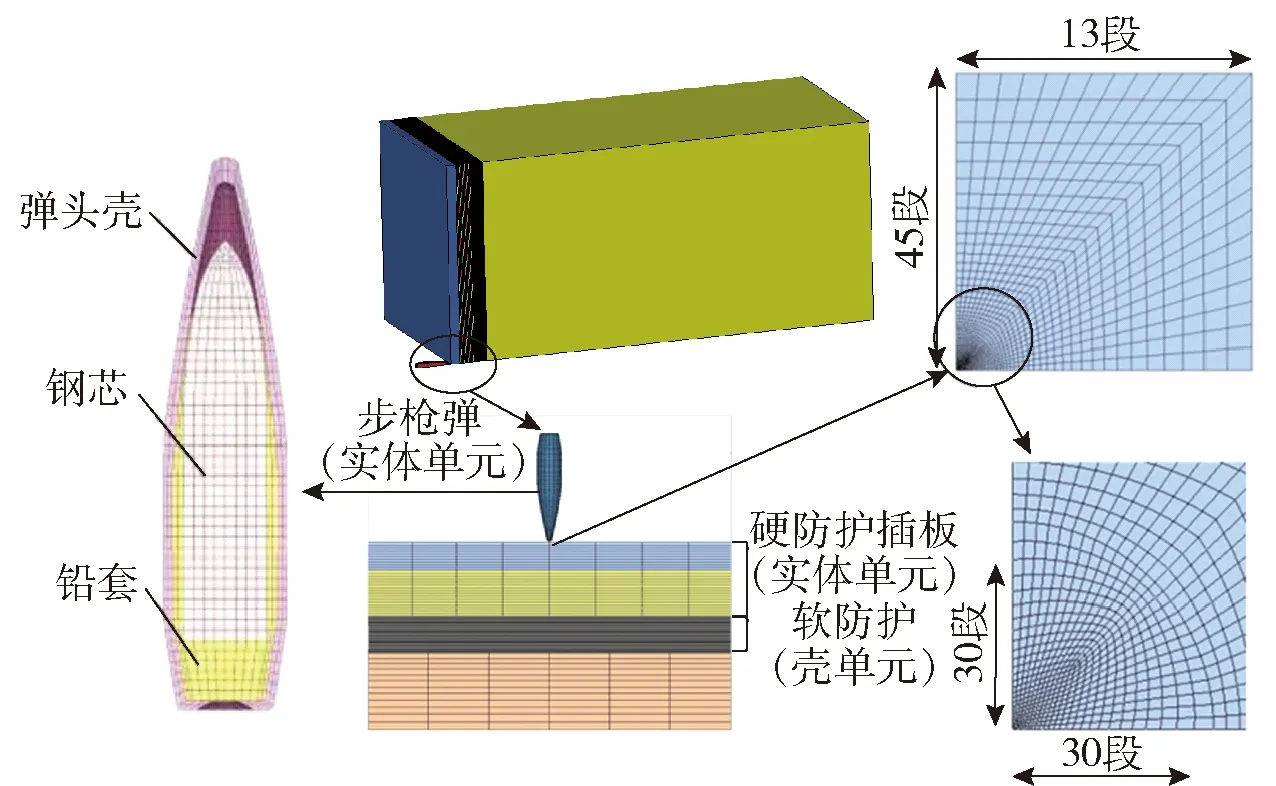
图2 步枪弹侵彻带软硬复合防护明胶靶标的有限元模型Fig.2 FE model of rifle bullet penetrating into the gelatin target with soft/rigid composite armor

侵彻过程中钢芯、铅套与弹头壳的动态力学行为采用Johnson-Cook模型结合Gruneisen状态方程[12-13]来描述，材料参数根据文献[12-13]来确定，如表1所示。

表1 钢芯、铅套和弹头壳的材料参数

注：ρ为材料密度，G为材料剪切模量，a、b、c、n、m和d为Johnson-Cook本构模型中的材料常数，Tm为材料熔点，Tr为环境温度。

1.2.2 软硬复合防护有限元模型

步枪弹高速撞击带软硬复合防护的明胶靶标时，软硬复合防护的材料变形与破坏主要发生在弹着点周围，远离弹着点的区域没有明显变形破坏。为兼顾计算效率与计算精度，将软硬复合防护在弹着点周围区域的网格细化：陶瓷板、背板和软防护在以弹着点为中心的5倍半径区域划分30段，之后向外划分逐渐稀疏，划分15段，外侧均划分13段；采用实体单元Solid164划分陶瓷板和UHMWPE背板的网格，选择壳单元Shell163划分软防护的网格。

采用Johnson-Holmquist模型来描述陶瓷的动态力学行为[12]，主要的材料参数根据文献[12]进行赋值，如表2所示。UHMWPE背板和软防护的动态力学行为由Mat_Composite_Failure_Option_Model材料模型来描述，该模型包含了8种失效模式，背板和软防护的材料参数根据文献[12-13]来确定，分别如表3和表4所示。

表2 陶瓷材料参数

注：A、B、C、M、N、D1和D2为Johnson-Holmquist为本构模型中的材料常数，T为材料拉伸强度，HEL为雨果尼奥弹性极限，pHEL为雨果尼奥弹性极限下的压力，K1为材料体积模量，K2和K3为材料常数。

表3 UHMWPE背板材料参数

表4 软防护材料参数

>1.2.3 明胶有限元模型

由于高速侵彻过程具有瞬时性与局部性，明胶受压力波传播和软防护变形挤压作用，动态冲击响应集中在弹着点周围5倍弹径范围内，表现为明胶的半椭球形凹陷变形，而其余区域没有明显变形。采用实体单元Solid164对明胶进行网格划分时，在弹着点附近的区域细化网格，周边较疏，同时沿着弹道方向(z轴正方向)，网格不断变疏。采用弹塑性流体动力材料模型和线性多项式状态方程来描述明胶的动态力学行为，并根据文献[12-13]来确定明胶的材料参数，如表5所示。

表5 明胶材料参数

注：E为材料弹性模量，σs为材料屈服极限，C0、C1、C2和C3为材料常数。

1.2.4 弹- 靶接触模型

在数值模拟模型中，边界条件的设置与试验一致，整体采用单点积分，明胶块设置沙漏控制。选择自动面面接触Contact_Automatic_Surface_to_Surface算法描述弹头壳、铅套与钢芯3部分之间的相互作用，采用面面侵蚀接触Contact_Eroding_Surface_to_Surface算法来处理弹头与复合靶标各种材料(陶瓷复合插板、软防护和明胶靶标)的接触关系，陶瓷板与背板之间的接触设置为固连失效接触，背板与软防护及软防护与明胶靶标之间的接触均设置为自动面面接触Contact_ Automatic_Surface_to_Surface. 数值模拟模型中没有考虑背板层与层之间的胶粘材料，在背板内设置自动单面接触Contact_ Automatic_Surface_to_Surface算法来处理背板层与层之间的相互作用关系。

1.3 试验验证

弹道射击试验布置如图3所示，试验中采用弹道枪发射步枪弹，枪口距复合靶标迎弹面的距离为25 m，枪弹垂直撞击带软硬复合防护的明胶靶标，步枪弹着靶速度采用西安工业大学生产的XGK-2002型高灵敏度光幕靶来测量。在明胶靶标内距离迎弹面40 mm位置处埋设4个美国PCB压电有限公司生产的ICP-113B22型压力传感器，用于测量明胶靶内压力，传感器布置在半径为25 mm的圆周上，呈正方形分布，射击瞄准点为传感器布置中心位置。采用美国约克科技公司生产的Phantom V710高速相机来记录弹- 靶相互作用过程，相机放置在带软硬复合防护明胶靶标的侧面，并通过Phantom图像控制处理软件来测量明胶的凹陷变形情况，拍摄帧频为25 000帧/s.

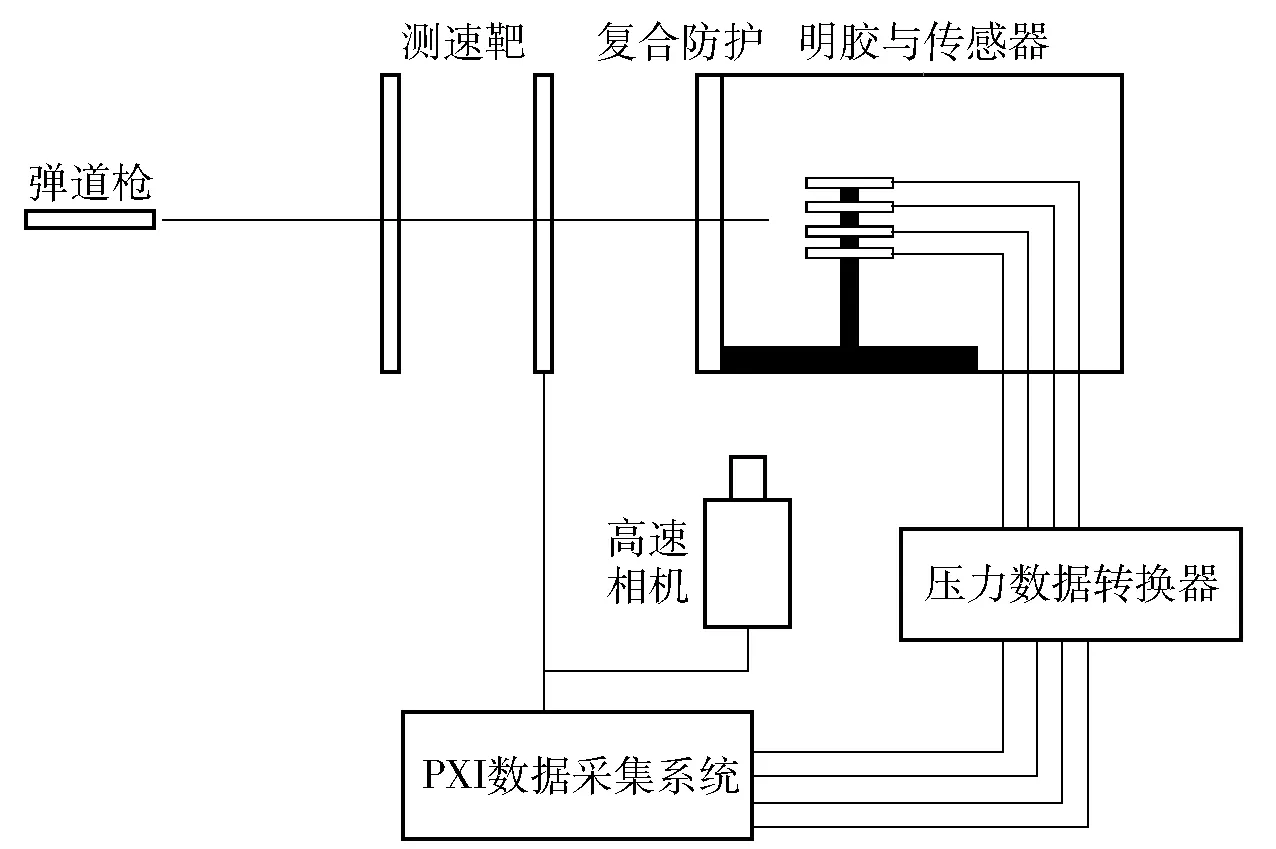
图3 弹道试验示意图Fig.3 Ballistic experimental setup

数值模拟与试验结果都表明软硬复合防护有效阻止了步枪弹的穿透：步枪弹穿过陶瓷板后继续侵彻UHMWPE背板，最终停留在背板内。弹头在侵彻过程中受到陶瓷板的阻挡，头部镦粗变形，最后呈现明显的蘑菇头形状，如图4所示，数值模拟得到的弹头形状与试验结果基本一致。表6给出了数值模拟获得的典型参数与试验结果的对比，数值模拟结果中的弹头剩余长度、穿透深度以及明胶中测点的压力峰值与试验结果误差均小于10%，表明所建立的数值模拟模型具有较好的准确性和可信度，能够有效地模拟该步枪弹对带软硬复合防护明胶靶标的侵彻作用过程以及弹头、防护和明胶靶标的动态响应。

图4 数值模拟与试验的残余弹形对比Fig.4 Comparison of simulated and experimental results

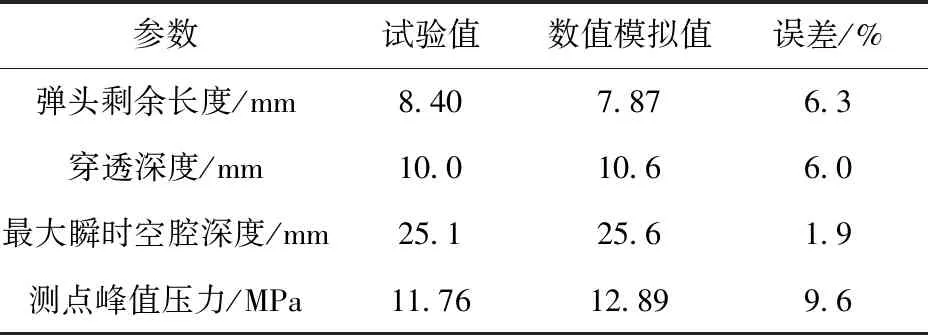
参数试验值数值模拟值误差/%弹头剩余长度/mm8.407.876.3穿透深度/mm10.010.66.0最大瞬时空腔深度/mm25.125.61.9测点峰值压力/MPa11.7612.899.6

2 数值模拟结果与分析

2.1 能量传递分析

创伤弹道学研究表明，能量传递是造成目标损伤的主要因素，因而首先分析弹头对带软硬复合防护明胶靶标的侵彻过程中，弹头、明胶以及软防护能量的变化情况，结果分别如图5和图6所示。在步枪弹侵彻陶瓷复合插板的过程中，步枪弹的动能有一段明显的下降过程，由10 μs时的1 581 J快速下降到35 μs时的476 J；同时，有一部分能量开始传递到软防护和明胶中。由于压力波传播和软防护变形挤压的双重作用，明胶弹着点附近区域开始发生显著压缩变形。从图6中可以发现明胶中的能量最大时为22.3 J，软防护中的能量最大时为28 J，而步枪弹弹头的初始能量为1 652 J，传递到明胶的能量最大时仅占弹头初始动能的1.3%，表明放置在明胶靶标前面的陶瓷复合插板和UHMWPE软防护对步枪弹的侵彻有着明显的防护效果，大大减少了传递至明胶靶标的能量。

图5 弹头动能变化情况Fig.5 Kinetic energy variation of bullet

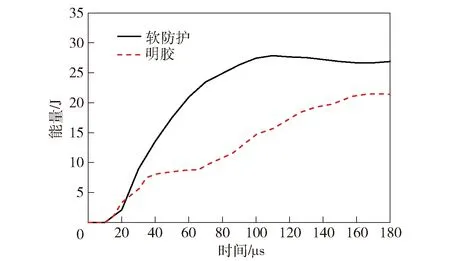
图6 明胶与软防护能量变化Fig.6 Variation of energy transmitted to gelatin and soft armor

在图5中选取了tA、tB两个明显的能量变化特征点，其中tB点为弹头与UHMWPE背板接触时刻，约为35 μs. 对弹头能量在tA、tB两点之间的数据进行拟合，得到在这一阶段中能量变化的解析式为

Eb=2 029-43t，

(1)

式中：Eb为弹头动能(J)；t为在陶瓷面板内的运动时刻，5 μs≤t≤35 μs.

从(1)式中可以发现，弹头在侵彻陶瓷板的过程中其能量随时间变化呈线性衰减，利用该解析式可以估算弹头在侵彻陶瓷板时任意时刻的剩余能量。

进一步分析弹头能量随侵彻深度的变化情况，如图7所示，弹头对陶瓷复合插板的侵彻深度为10.6 mm，而陶瓷板的厚度为7 mm，表明弹头对陶瓷复合插板的侵彻以陶瓷板为主。在弹头侵彻陶瓷板的最初阶段，弹头头部的锥头部分完成了对陶瓷板的开坑，弹头进入陶瓷板内，此时弹头直径基本不变，弹头速度下降较少，能量消耗也较小；随着弹头对陶瓷复合插板侵彻深度的增加，弹头的圆锥段逐渐破碎侵蚀，弹头形状开始发生改变，质量逐渐减少；弹头镦粗变形，与陶瓷复合插板的接触面积变大，侵彻速度明显下降，弹头动能消耗也逐渐增大。从图7可以看出：弹头侵入一定深度后，侵彻单位厚度陶瓷消耗的能量一定；弹头的大部分动能消耗在侵彻陶瓷板过程中，侵彻陶瓷板结束时，弹头剩余的动能约为476 J，与弹头初始动能相比，弹头的动能减小了约71.2%，减少的能量主要以弹体塑性变形、侵蚀与发热，陶瓷裂纹形成与扩展、飞溅以及UHMWPE背板变形等方式消耗了；随后弹头继续侵彻UHMWPE背板，直至侵彻深度最大时，弹头速度衰减为0 m/s，在这一阶段，剩余的弹头动能主要由UHMWPE背板塑性变形吸收；此外，弹头进一步镦粗变形，还有一小部分能量继续传递至软防护和明胶靶标。

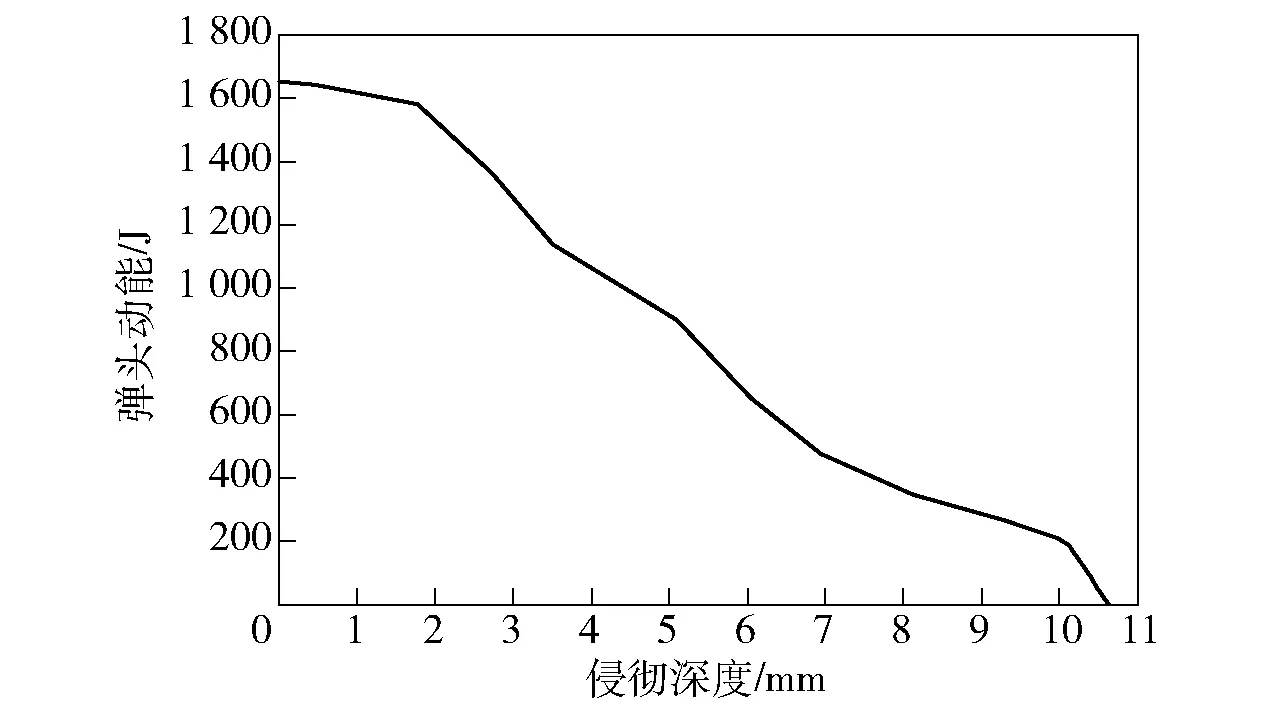
图7 弹头动能随侵彻深度的变化情况Fig.7 Bullet kinetic energy vs. penetration depth

2.2 明胶靶标瞬时空腔响应分析

试验与数值模拟结果都显示在明胶靶标上出现了瞬时空腔，在0～1 500 μs时，试验和数值模拟的明胶瞬时空腔凹陷深度随时间变化对比结果如表7所示，结果表明瞬时空腔深度在约1 500 μs时达到最大值。在步枪弹高速撞击作用下，软硬复合防护发生快速变形，并挤压弹着点下的明胶，使得明胶开始发生压缩变形，并逐渐发展为形状近似于半椭球形的瞬时空腔。随着弹头对陶瓷复合插板侵彻深度的不断增加，防护的凹陷变形不断增大，传递至明胶的能量也逐渐增加，明胶内瞬时空腔的凹陷深度也逐渐增大：在500 μs时，瞬时空腔的凹陷深度为17.8 mm；在1 500 μs时，凹陷深度为25.6 mm；此外，数值模拟结果表明明胶瞬时空腔的膨胀速度最大可达35.7 m/s. 如表7所示，可以发现数值模拟的明胶瞬时空腔凹陷深度与试验结果具有很好的一致性。

表7 数值模拟与试验结果的明胶空腔凹陷深度对比

明胶中等效应力随时间变化的分布情况如图8所示，可以看出明胶中的等效应力作用区域形状为一半球状，球心位于弹着点，与瞬时空腔形状类似。最大等效应力界面始终位于瞬时空腔的边缘区域，且距弹着点越远，应力越小。

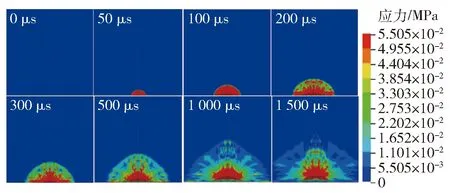
图8 明胶靶标内等效应力演化过程Fig.8 Evolution of Von Mises equivalent stress in gelatin

2.3 明胶靶标压力场分析

数值模拟结果表明明胶内的压力场变化与等效应力变化相似，都以弹着点为球心，以球面波的形式向外传播，如图9所示。最开始时，明胶弹着点处的峰值压力最大，随着时间的推移，压力波的传播范围逐渐增大，当压力波传播至明胶的自由界面时发生反射，反射的压力波与原先向外传播的压力波相互干涉。根据压力从弹着点传递到不同距离位置处的距离差Δs除以相应的时间差Δt可以获得压力波在明胶中的传播速度v，即v=Δs/Δt，数值模拟计算得到的压力波传播速度约为1 450 m/s，试验中测得的传播速度约为1 470 m/s，二者基本一致。

图9 典型时刻明胶靶标压力场分布云图Fig.9 Distribution of pressure field in the gelatin target at typical time

明胶中压力测量位置处的压力随时间变化曲线的数值模拟和试验结果如图10所示，由于压力波传播和防护材料的快速变形挤压作用，约47 μs时，明胶内的压力迅速增大，到约57 μs时，数值模拟得到的峰值压力达到12.89 MPa，试验中测得的峰值压力为11.76 MPa，二者误差小于10%，表明数值模拟结果与试验吻合得较好。此外，与Luo等[15]研究发现的明胶内压力双峰值现象相似，在步枪弹高速撞击带软硬防护明胶靶标过程中，随着弹头侵彻撞击UHMWPE背板，压力曲线中出现了第2个峰值压力(6.74 MPa)，与第1个峰值压力间的时间间隔约为15 μs.

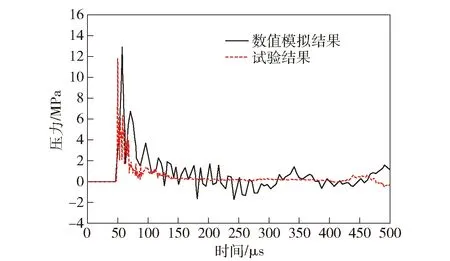
图10 明胶靶标内测压位置处的压力曲线Fig.10 Curves of pressure in gelatin at the measured location

2.4 软硬复合防护破坏过程与弹- 靶侵彻作用分析

2.4.1 防护层应力变化与破坏特性

弹头高速撞击陶瓷复合插板时，在陶瓷板内产生了压力波，压力波沿靶标的横向和纵向传播，陶瓷板上弹着点及其周围区域开始出现裂纹并逐渐扩展，如图11(a)所示。当压力波传播至陶瓷板与UHMWPE背板界面处时，由于这两种材料的波阻抗差异较大，在界面处会反射形成拉伸波，拉伸波的传播方向与弹体前进方向正好相反。受压缩的陶瓷材料会产生膨胀，由于陶瓷的抗拉强度较低，反射的拉伸波使界面处的陶瓷开始产生裂纹、损伤，在弹头撞击陶瓷板后约10 μs时，陶瓷锥基本形成，该时间与Reijer[20]提出的陶瓷锥形成时间计算方法得到的计算结果基本一致。

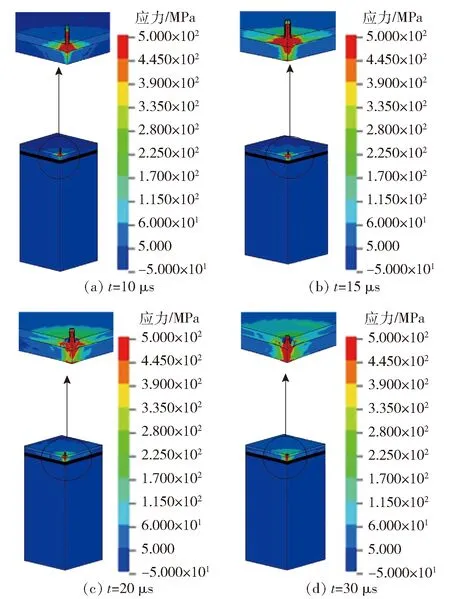
图11 撞击区域应力分布云图Fig.11 Stress in the impacted zone

由陶瓷复合插板与软防护组成的软硬复合防护的抗弹机理主要体现在“碎”与“阻”：高硬度、高强度陶瓷板使得弹头破碎、镦粗，从而使弹头侵蚀、速度下降；而软防护则进一步阻挡弹头的侵彻，同时把载荷分散到更大的接触面积上，减小对有生目标机体造成钝性损伤。陶瓷复合插板在阻止弹头侵彻和消耗能量方面起主要作用，弹头在侵彻软硬复合防护的过程中伴随着界面驻留、弹头破碎与变形、UHMWPE背板变形、软防护变形以及明胶靶内的瞬时空腔等现象。在弹头侵彻陶瓷板的过程中，陶瓷板在拉应力和压应力的反复作用下开始出现裂纹，并逐步扩展、破碎及飞溅。图12为陶瓷锥演化过程中应变变化的数值模拟结果，从中可以发现，在陶瓷锥的中心区域和边缘区域由于分别受到压力波和拉伸波的作用，相应地出现了负应变和正应变，且陶瓷板内超过失效应变的陶瓷材料区域与陶瓷锥形状基本相似。此外，从图11和图12中还可以看出，当弹头开始侵彻背板时，背板和软防护开始发生变形，在软防护快速撞击下，明胶也逐渐发生凹陷变形，形成空腔，弹头对陶瓷复合插板的侵彻过程结束后，明胶靶标发生长时间的膨胀- 收缩以消耗传递至明胶内的能量。

图12 陶瓷锥演化过程中的应变变化Fig.12 Strain variation during the evolution of ceramic cone

2.4.2 弹头运动变化特性

在侵彻软硬复合防护的过程中，弹头速度和加速度随时间变化的曲线如图13所示，从中可以发现侵彻过程中：步枪弹速度首先快速下降，然后逐渐减少至0 m/s；而加速度绝对值则在0～20 μs阶段内快速增大，随后略微衰减、经历了第2个加速度峰值，而后在50～110 μs内逐渐衰减趋于0 m/s2. 根据弹头在侵彻过程中不同时刻的位置与形态，分别在加速度和速度曲线上选取4个特征点：在加速度曲线上，A1点为弹头运动初始时刻，B1点为加速度绝对值最大时刻，C1点为弹头头部与背板层接触面积最大时刻，加速度曲线出现了第2个峰值特征点，D1点是加速度衰减为0 m/s2的时刻；在速度曲线上，A2点为弹头运动初始时刻，B2点为与B1点相同的时刻，C2点为弹头头部基本穿过陶瓷板开始接触背板层的时刻(C1和C2为不同时刻)，与图5中tB点时刻一致，D2点为弹头速度为0 m/s的时刻。根据弹头加速度绝对值的衰减变化过程，可以将该步枪弹侵彻带软硬复合防护明胶靶标过程分成3个阶段：

1)陶瓷层内开坑阶段(A1B1段)。当高速运动的弹头头部开始侵彻陶瓷板时，由于防弹陶瓷材料具有很高的硬度和抗压强度，在弹头上产生很大的动态载荷，弹体的加速度绝对值迅速增大，弹头壳与铅套材料向外流动、发生变形和质量侵蚀，钢芯也开始镦粗。同时，在弹头的高速撞击下，陶瓷板内开始出现裂纹，当弹头头部弧形段侵彻进入陶瓷板时，弹头加速度的绝对值达到最大，在开坑过程中，弹坑直径大于弹头直径。

2)陶瓷层内稳定侵彻阶段(B1C1段)。陶瓷板由于冲击破碎，对弹头的阻力减小，后期以摩擦力为主。在此过程中，弹头的圆柱部逐渐穿透陶瓷锥，不断嵌入陶瓷层内，同时受到背板阻力和破碎陶瓷材料的摩擦作用，加速度绝对值逐渐减小，进入稳定侵彻阶段。在C2点时刻，弹头头部开始接触背板层，弹体受到的阻力再次增大，至C1点弹头加速度绝对值达到第2个峰值，弹头镦粗形态基本形成，头部镦粗直径达到最大，弹头完成了在背板层内的开坑。

3)背板侵彻阶段(C1D1段)。C1点为弹头头部与背板层接触面积最大时刻，加速度曲线出现第2个拐点，弹头头部部分嵌入UHMWPE背板，此时主要受到背板的阻力作用，加速度绝对值逐渐减小，直至减小为0 m/s2. 弹头的残余动能主要由UHMWPE背板变形吸收，背板的鼓包量逐渐增大直至弹头停留在背板内。

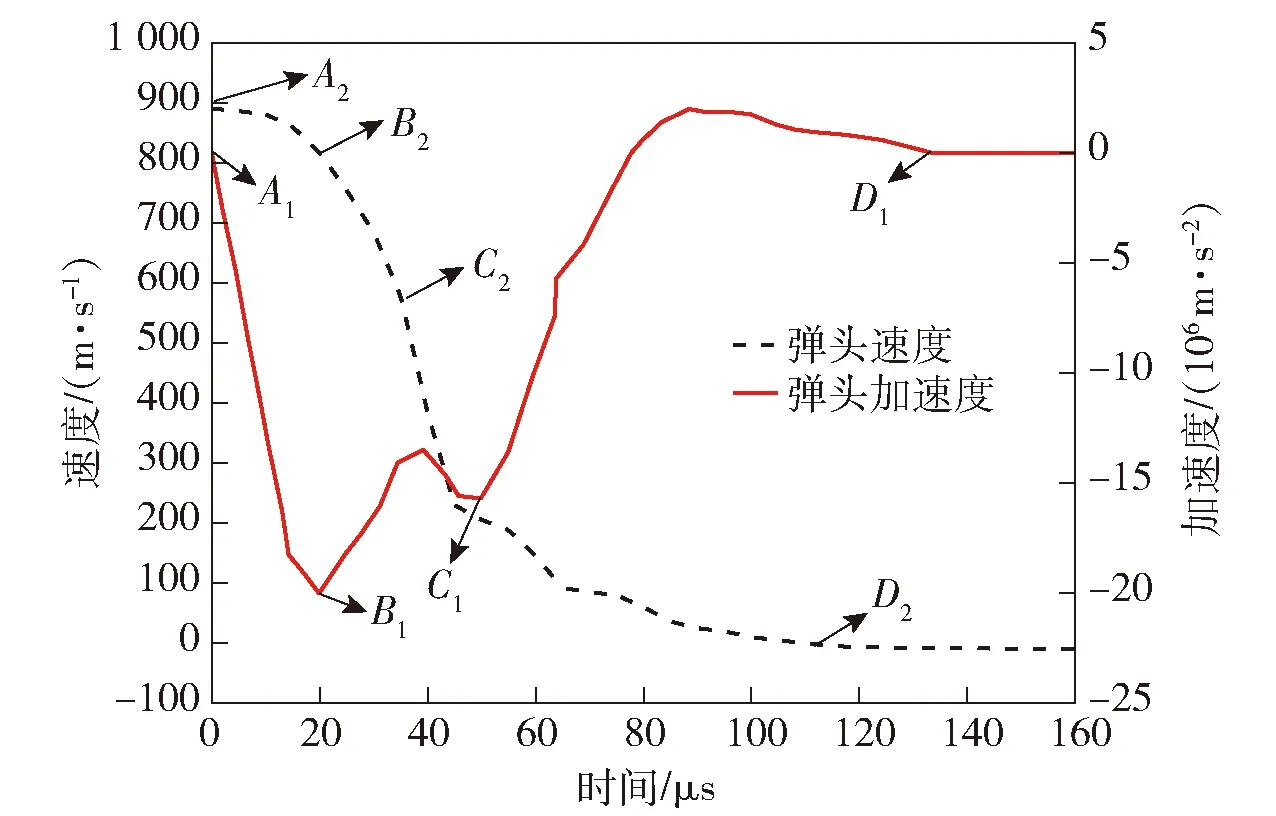
图13 步枪弹速度和加速度变化曲线Fig.13 Curves of bullet velocity and acceleration

在侵彻软硬复合防护的过程中，弹头发生界面驻留、材料流动、质量侵蚀和钢芯镦粗等现象。结合图12和图13可以发现：弹头变形过程主要发生在侵彻过程的前40 μs，在界面驻留阶段，弹头头部材料向外流动，发生磨损和质量侵蚀，弹头开始镦粗变形，与陶瓷板的相互作用面积逐渐增大；在侵彻UHMWPE背板的过程中，随着钢芯的进一步镦粗和侵蚀，对背板的侵彻速度逐渐下降。比较速度曲线中的A2C2段与C2D2段，可以发现A2C2段斜率较大，即在侵彻的前35 μs内，弹头速度降较大，表明陶瓷的阻挡对于弹头动能的降低起主要作用。

3 结论

1)本文建立了某步枪弹侵彻软硬复合防护下明胶靶标的数值模拟模型，该模型数值计算结果与试验结果在弹头剩余长度、穿透深度以及明胶内峰值压力等典型参数的误差均小于10%，验证了数值模拟模型的准确性和合理性。

2)在弹头侵彻复合靶标的过程中，弹体的大部分动能(约71.2%)消耗在侵彻陶瓷板阶段；侵彻结束时，弹头没有穿透UHMWPE背板，对陶瓷复合插板的最大侵彻深度为10.6 mm；传递至明胶的能量最大时仅为弹头初始动能的1.3%，表明陶瓷复合插板和UHMWPE软防护对步枪弹的侵彻有着明显的防护效果，可以有效减少传递至明胶的能量。

3)带软硬复合防护明胶靶标受步枪弹高速撞击后，由于防护材料的快速变形压缩作用，弹着点周围的明胶开始出现变形，形成类似于半椭球形的瞬时空腔，该空腔随时间推移逐渐膨胀，瞬时空腔最大凹陷深度为25.6 mm，最大膨胀速度为35.7 m/s.

4)该步枪弹高速撞击软硬复合防护下明胶靶标的过程中，明胶内的等效应力范围呈现半球形，球心位于弹着点，最大等效应力一直处于明胶凹陷变形的边界处，且距离弹着点越远，等效应力越小。压力场的演化过程与等效应力情况相似，撞击初始时，明胶内弹着点处的峰值压力最大，而后峰值压力大小随着传播距离的增大而不断减小。

5)在侵彻复合靶标过程中，弹头速度最初有一段显著的下降过程，而后逐渐减少至0 m/s；在0～20 μs时，加速度绝对值迅速增大，而后在50～110 μs时逐渐衰减趋于0 m/s2. 陶瓷板的破坏区域集中在弹着点附近，拉应力和压应力的反复作用是陶瓷板发生破坏的主要原因。