C形一体电枢的结构设计及接触压力分析

范薇，苏子舟，范天峰，张涛，张洪海，刘勇

(西北机电工程研究所，陕西 咸阳 712099)

0 引言

电磁炮是一种新概念武器，主要包括电磁轨道炮和电磁线圈炮[1-3]。轨道炮使用的C形一体电枢结构，其设计前提是保证发射过程中电枢与轨道(以下简称枢轨)之间保持良好的金属—金属接触，避免发生转捩。枢轨之间接触面大小和位置的分布以及二者之间接触压力的大小均是导致转捩的重要因素，接触面与接触压力的大小都与电枢的结构有关[4-8]。因此，研究枢轨之间电接触特性，对合理设计电枢结构、提高电磁轨道炮发射效率以及抑制轨道烧蚀、转捩，均有着重要意义。

电磁轨道炮枢轨间的滑动电接触受多种因素影响，如接触压力、电枢运动速度、脉冲电流等。原则上枢轨接触面越大越好[9-11]。然而，由于在速度趋肤的影响下电流容易向电枢尾翼集中，引起尾翼烧蚀；且由于电枢运动过程中的振动和应力变形等原因，使得电枢仅部分表面与轨道接触。因此，应考虑从枢轨有效接触面设计的角度对电枢结构进行优化设计。

通过研究发射初始阶段电枢与轨道接触压力来保证枢轨良好的接触，是C形电枢设计的另一个重要方面[12]。发射初期过盈配合所提供的接触压力能否满足发射需求，通常用Marshall的“安克法则”(“1 g/1 A”)来判断，即要顺利通过1 kA电流而不发生起弧，至少必须提供10 N的接触压力挤压轨道。在脉冲电流未建立起来之前，接触压力主要由过盈配合产生的机械预压力提供；电流建立起来之后，电磁力占主导地位[13-15]。实际发射过程中，轨道受力是瞬态变化的，且电枢侧面与轨道表面不可能完全接触，如果枢轨结构设计不合理，则可能会导致枢轨之间接触压力不足的情况。因此，枢轨间接触压力设计应在考虑发射组件瞬态受力状态的情况下对“安克法则”进行修正优化，形成“安克法则”瞬态应用方法，且基于轨道优化试验平台计算枢轨接触压力并进行试验[4-8]。

本文主要针对方口径电磁轨道炮，基于关键参数设计，首先提出了电枢设计需要满足枢轨接触面设计，通过使用Ansoft软件高频涡流场计算枢轨电磁场特性，研究了不同接触面大小和位置对电枢电磁受力和电流密度的影响规律，获得了枢轨接触面大小与接触范围。其次从发射起始段电枢与轨道的接触状态出发，通过使用ANSYS软件模拟发射起始段电枢与轨道的装配情形，在电磁轨道发射器几何尺寸不变的情形下，运用“安克法则”瞬态应用方法计算分析了瞬态条件下不同接触面的接触压力。计算结果表明该方法能够有效地模拟枢轨接触压力瞬态变化特性。该方法设计的电枢在多次发射试验[16-18]中，轨道起始阶段没有烧蚀引起的刨坑，实现了较好的起始段电接触性能。通过试验数据得出的接触压力与仿真结果基本一致，验证了“安克法则”瞬态应用方法的准确性。

1 C形电枢的关键结构参数设计

轨道炮发射过程中，电枢受到的洛伦兹力方向为电流密度J×磁场B，在平面上可以分解为电磁推力Fe和电磁压力Ne两个分量。由于轨道产生的磁场B实际上由电流密度J的分布决定，电枢的总体受力情况取决于电流密度J的分布，而J的分布与电枢几何结构有密切的关系。图1给出了一类C形电枢的结构示意图。图1中：P为电枢与轨道内表面接触的切点；O为参考线OP的起始点；Re为电枢头部的外半径；Rn为电枢头部的内半径，且其内弧段同时与参考线OP及电枢的内部直边相切；Ls为电枢尾翼长度；d为电枢尾翼厚度；φ为电枢尾翼夹角；j为流经电枢的电流密度。

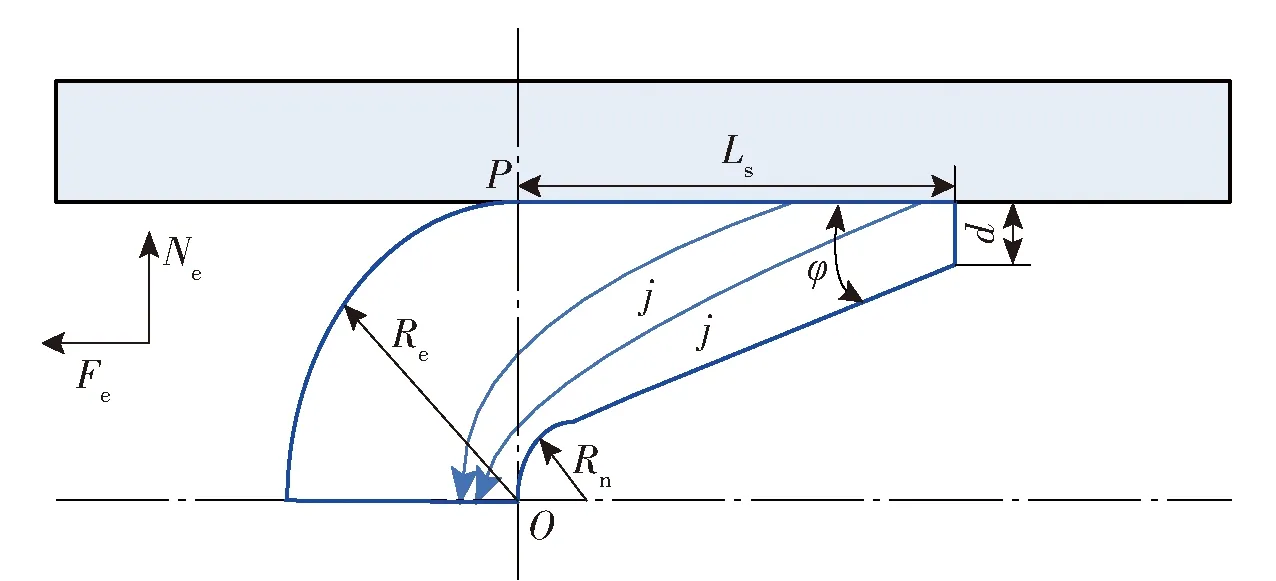
图1 电枢结构尺寸示意图Fig.1 Schematic diagram of armature structure

如图2所示，由于电枢在膛内运动的时间很短(<10 ms)，在电流趋肤(含速度趋肤)效应的影响下，电流密度在O点的临域内最大，越靠近电枢头部外围，电流密度的分布越小，因此电枢头部外侧所受的电磁力远小于电枢尾翼附近处的电磁力。对于此类电枢的设计问题就转化为d、Ls及Rn的选取问题。

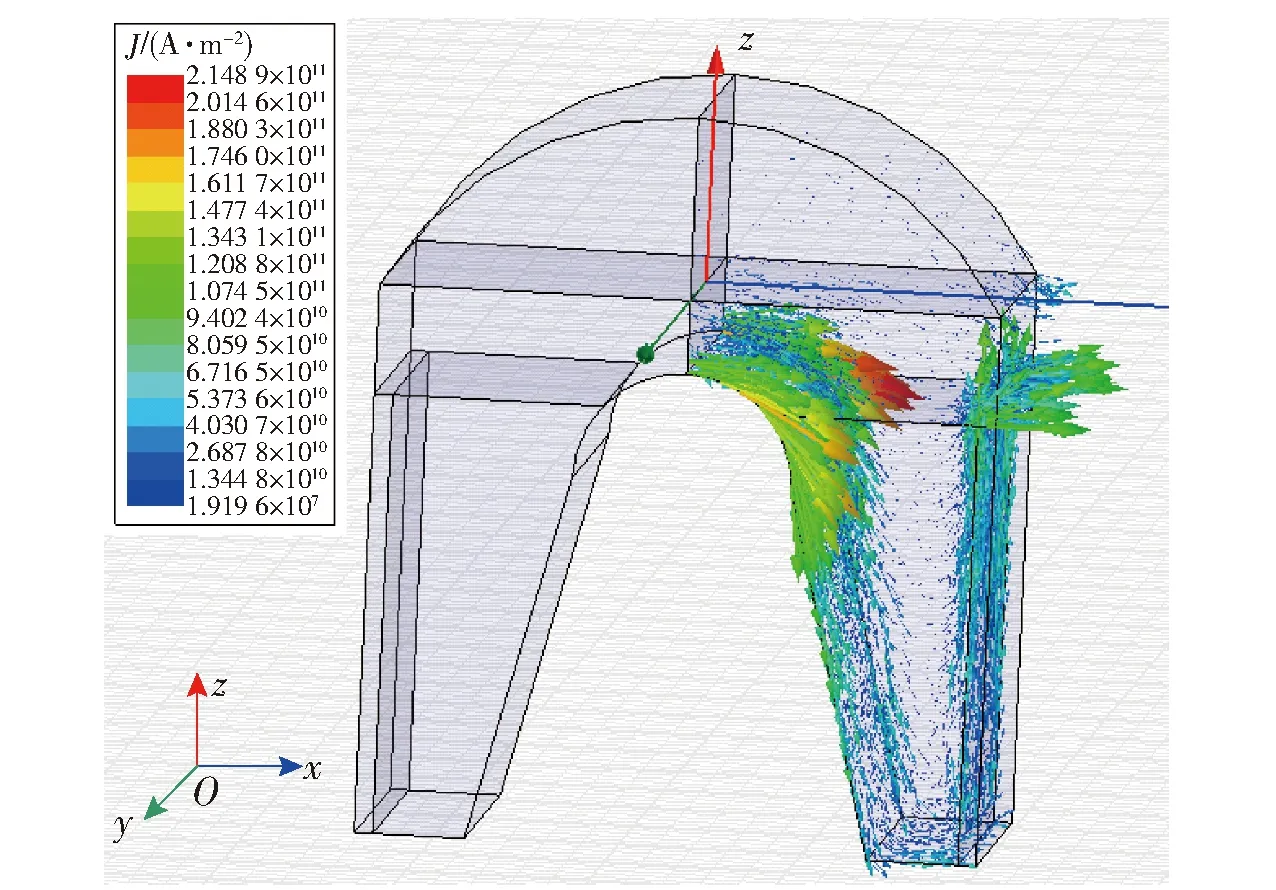
图2 电枢电流密度分布云图Fig.2 Nephogram of armature current density distribution

通过前期对电枢关键参数的电磁场计算分析的研究可知，内圆半径Rn和电枢尾翼厚度d对电磁推力和压力的影响都不大。因此，在电枢设计时，只需要保证尾翼载流能力即可。基于该结论，可从枢轨接触面的角度，通过计算分析电枢的电磁特性及接触压力来优化电枢结构。

2 仿真计算

2.1 计算模型

2.1.1 枢轨接触电枢分块计算模型

在Ansoft仿真软件中建立的电枢分块模型(由于对称性，只计算1/2模型)如图3所示，将电枢与轨道接触部分材料定义为铝，将电枢与轨道接触但不导电薄层部分材料定义为空气，使其在几何上与轨道接触但电气上不接触。轨道、外壳及金属板材料为铜，电枢材料为铝。

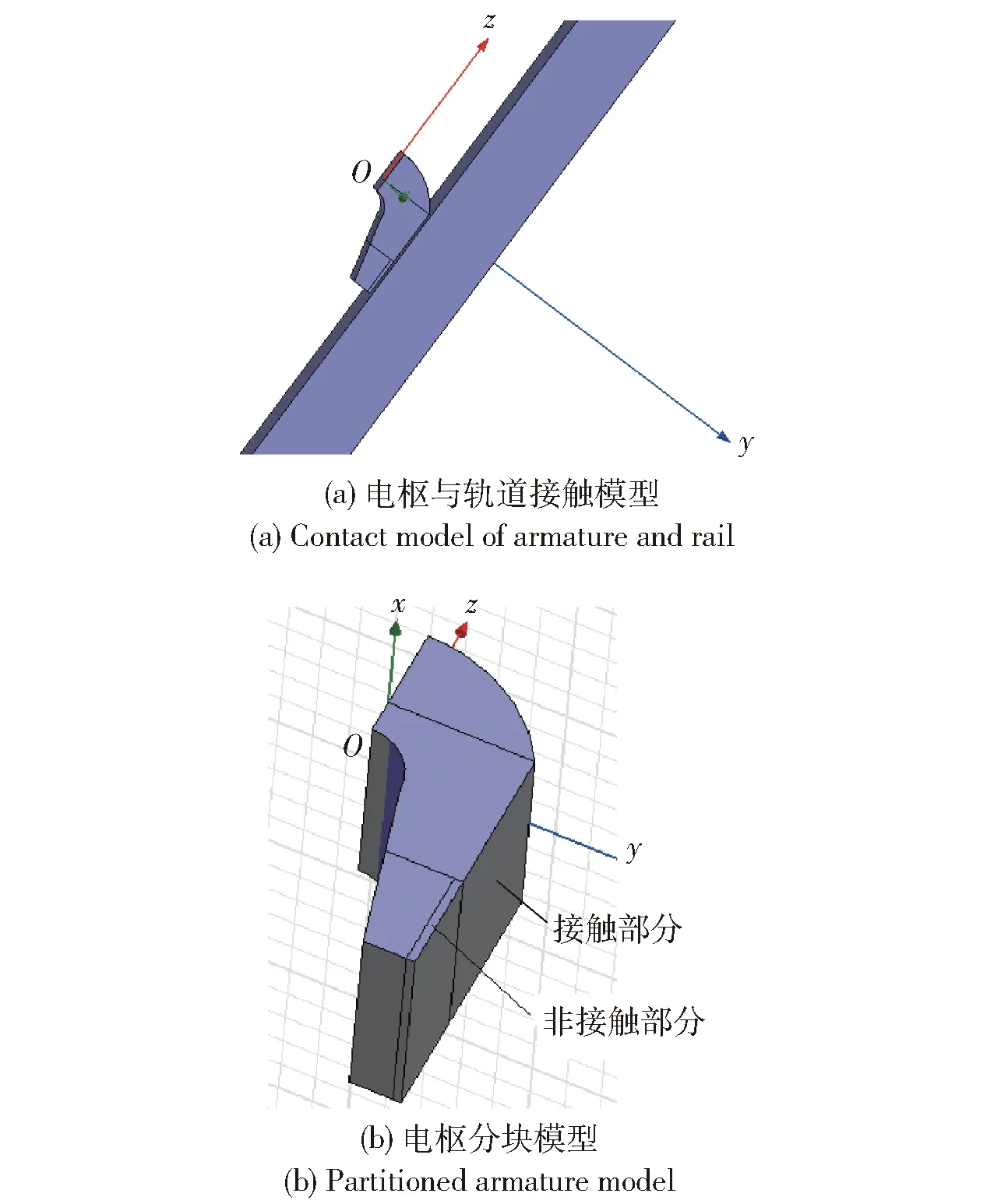
图3 电枢分块与轨道接触模型Fig.3 Contact model of armature and rail

2.1.2 枢轨接触压力计算模型

基于轨道优化试验平台，在ANSYS Workbench软件平台建立枢轨接触压力计算模型，如图4所示。由于结构的对称性，为减小计算规模，建立1/2枢轨接触模型，轨道长取100 mm. 假设电枢与轨道接触为无摩擦，瞬态电流激励如图5所示，图5中0～t0表示电枢运动起始阶段，t0时刻为0.3 ms.

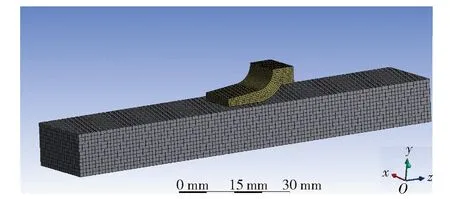
图4 电枢与轨道接触压力计算模型Fig.4 Calculation model of contact force between armature and rail

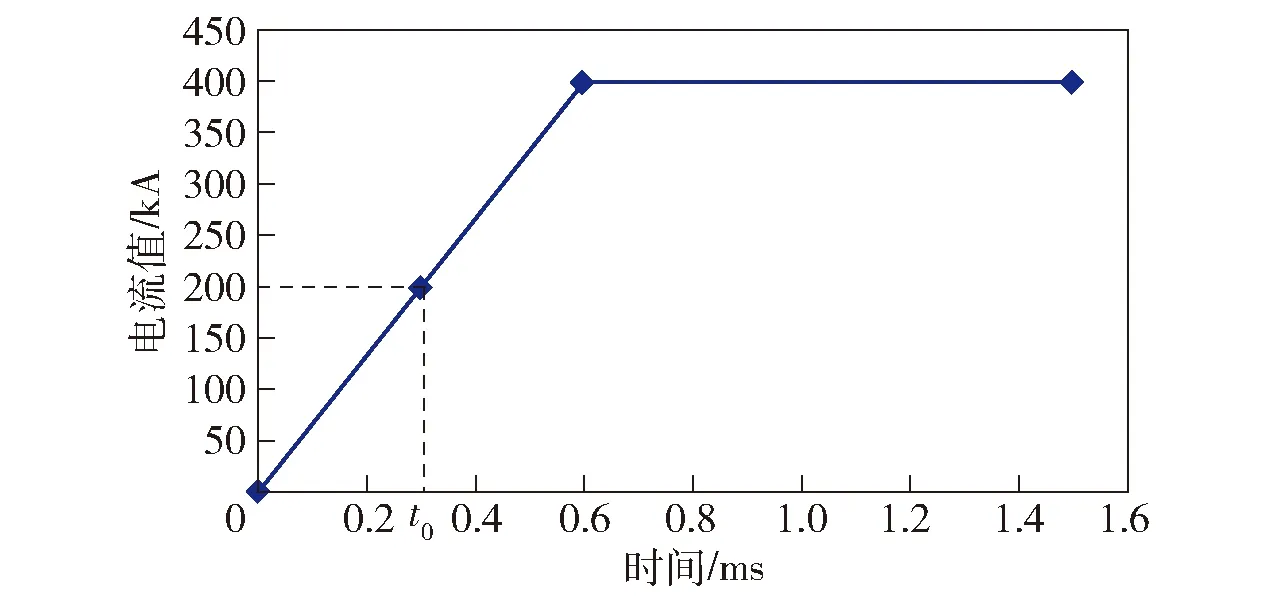
图5 电流激励曲线Fig.5 Current excitation curve

2.2 枢轨接触面对电枢电磁特性的影响分析

电枢与轨道接触面位置和大小对电枢所受电磁推力和电磁压力有很大的影响。为分析其影响规律，将电枢进行分块建模，电枢分块模型如图3(b)所示。假设电枢与轨道接触长度为Lc，其他部分与轨道不接触，电枢与轨道接触比为Lc/Ls.

2.2.1 电磁场计算原理及边界条件

由于电枢运动产生了涡流效应，选用高频涡流场作为仿真平台，等效模拟电枢运动引起的电流集肤效应下电枢轨道接触面大小与位置对电枢电流密度分布、电磁压力与电磁推力的影响规律。

2.2.2 仿真计算

使用Ansoft软件的高频涡流场平台，加载图5所示电流曲线峰值400 kA、频率200 Hz的电流激励，计算接触面分别从头部开始、从尾部开始、从中部开始3种接触情况下，随着Lc/Ls从小(电枢与轨道接触比为2%)到大(电枢与轨道接触比为100%)，电枢最大电流密度分布与电枢电磁受力，结果如图6～图8所示。图7中：电磁推力为电枢整体在z轴方向(加速度方向)的电磁力；图8中，电磁压力为1/2电枢在y轴方向的电磁力。

图6 电枢电流密度的最大值曲线Fig.6 Maximum current density of armature

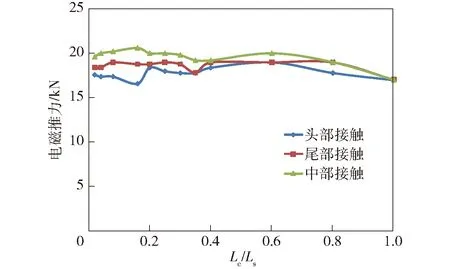
图7 电枢电磁推力曲线Fig.7 Armature electromagnetic thrust curves

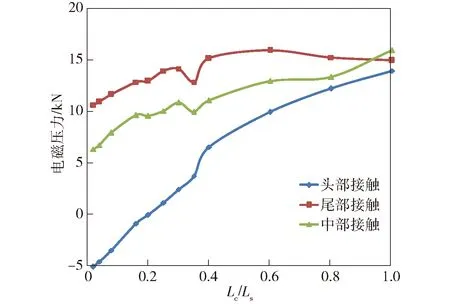
图8 电枢电磁压力曲线Fig.8 Armature electromagnetic pressure curves

从图6中可以看出，从限制电枢电流密度最大值的角度考虑，靠近尾部接触下的电流密度值最小。3种接触情况下，枢轨接触面在30%(Lc/Ls为0.3)以后均呈下降趋势，大于接触面40%以后呈现平稳状态，因此靠近电枢尾部30%～40%接触范围为有效接触。

从图7中可以看出：3种接触情况在枢轨40%接触面下的电磁推力曲线交于同一点，大于60%接触面时电磁推力减小，因此电枢与轨道有效接触面积小于电枢侧面积的60%条件下，可提高电磁推力；尾部接触与中部接触的电磁推力曲线基本一致，相差不大；头部接触下的电磁推力值最小。

从图8中可以看出，尾部接触的电磁压力最大。头部接触下电磁压力在接触比小于20%处出现负值，这是因为接触面过于靠近头部，使得电流密度反向分布，造成电磁压力方向。

综合上述分析可知，枢轨最佳接触状态为电枢与轨道接触面位置为靠近电枢后半部分，且大小为30%～60%.

2.3 电磁发射起始段枢轨接触压力计算与分析

2.3.1 传统接触压力计算方法—“安克法则”

目前，对于枢轨接触压力的计算准则是“安克法则”，即每通过100 kA电流至少须提供1 kN的接触压力。初始接触压力Nc由机械接触压力Nc1和电磁接触压力Nc2两部分组成。传统计算初始机械预应力过程有如下假设：

1)机械预压力Nme不随时间变化，全部转为接触压力Nc1；

2)电枢电磁压力Nem全部转为接触压力Nc2；

3)枢轨接触压力Nc只需满足“安克法则”，无最小值限制。

此设计过程可以描述为：找到一个枢轨结构设计，使得

Nc-Nag≥0，

(1)

Nc=Nc1+Nc2，

(2)

Nc1=Nme，

(3)

Nc2=Nem，

(4)

式中：Nag为“安克法则”等效力。

由(1)式可以看出，“安克法则”的计算准则是枢轨接触压力Nc曲线要在“安克法则”等效力Nag之上，这样才能避免枢轨接触失效。由(3)式、(4)式可以看出，机械预压力是定值，电磁压力全部用于电磁接触压力，忽略了轨道瞬态受力，且电枢侧面与轨道内表面可能没有充分接触，因此运用该方法设计的电枢可能会导致枢轨接触失效。

2.3.2 “安克法则”瞬态应用方法

本文在计算一体化电枢初始接触压力时，考虑对“安克法则”进行修正优化，将机械预压力Nme及电枢电磁压力Nem考虑为瞬态变量，即分别为Nme(t)与Nem(t). 这样电枢与轨道的过盈设计可描述为：找到一个枢轨结构设计，使得

Nc-Nag≥0，

(5)

Nc=Nc1+Nc2，

(6)

Nc1=Nme(t)，

(7)

Nc2=Nem(t)，

(8)

(9)

式中：K为电磁压力与枢轨电磁接触压力的比值。

修正后计算方法的核心是考虑枢轨瞬态受力情况下，使接触压力Nc随时间变化曲线位于“安克法则”等效力Nag线之上。

2.3.3 “安克法则”瞬态应用方法的接触压力计算

基于轨道炮优化试验平台，应用“安克法则”瞬态应用方法计算分析电磁发射起始阶段的枢轨接触压力变化趋势，验证修正后的“安克法则”瞬态应用方法能够有效地模拟枢轨接触压力瞬态变化特性。

2.3.3.1 瞬态机械预应力Nme(t)计算

在发射过程中，轨道随时间向外扩张，枢轨过盈量减小，导致预压力随时间减小，从而使得枢轨间的接触压力呈现瞬态变化特性。为保证电枢与轨道的初始接触良好，电枢与轨道需过盈配合。一般电枢与轨道单边过盈量在0.3 mm以内，与上升沿轨道扩张量在可比范围内。对于确定电枢而言，当轨道扩张量等于或超过电枢单边过盈量时，机械预压力完全失效，等于0 N.

在ANSYS Workbench平台建立的枢轨接触计算模型见图4. 以图5所示的瞬态电流曲线中0～t0(0～0.3 ms)时刻的电流对枢轨接触压力进行电磁场与结构场耦合仿真计算，所得的轨道扩张量随时间变化曲线如图9所示。由图9可见，在电流上升沿轨道扩张量逐渐增大，0.3 ms时达到0.1 mm. 轨道扩张量与枢轨过盈量密切相关，对于枢轨单边过盈量为0.3 mm的电枢而言，枢轨过盈量随时间变化曲线如图10所示。由图10可见，在0.3 mm时刻，电枢过盈量为0.19 mm，即在初始阶段，接触压力主要由枢轨过盈配合产生的机械预压力提供。结合枢轨过盈量与机械预压力曲线，获得机械预压力随时间变化曲线，如图11所示。

图9 轨道扩张量随时间变化曲线Fig.9 Curve of expansion quantity of rail over time

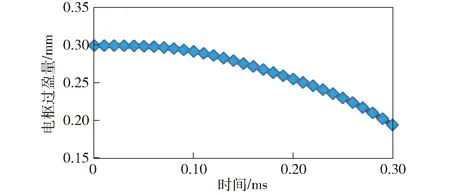
图10 电枢过盈量随时间变化曲线Fig.10 Curve of interference of armature over time

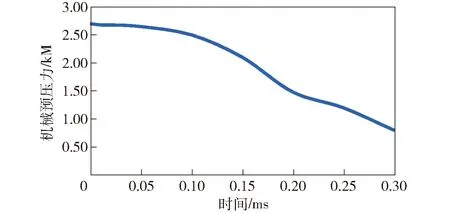
图11 机械预压力随时间变化曲线Fig.11 Curve of mechanical pre-pressure over time

从图11中可以看出，电枢轨道间机械预压力随时间从初始机械预压力逐渐减小直至800 N，远远大于0 N，因此可以保证电枢与轨道间的可靠接触。

2.3.3.2 不同接触面枢轨电磁接触压力、接触压力计算

发射起始段，电枢侧面与轨道内表面可能没有充分接触，由于电枢与轨道的动态受力状态，该接触表面也是瞬态变化的，定义电枢相对接触表面积：A=枢轨接触面积/电枢侧面积。

此外，电磁压力不能完全转化为枢轨之间的接触压力，其间存在一个转换系数如(9)式所示。

以轨道炮优化试验平台为例，电枢轨道接触模型如图4所示，加载图5中t0时刻即0.3 ms内的电流激励。计算当A分别取值为30%、50%、100%时枢轨的接触压力。首先在电磁场中计算电枢的电磁压力Nem；其次在ANSYS Workbench 平台中将电枢电磁压力求解结果作为计算输入与结构场进行耦合，计算枢轨电磁接触压力Nc2以及接触压力Nc.K的取值如图12所示，不同接触面的接触压力曲线如图13所示。

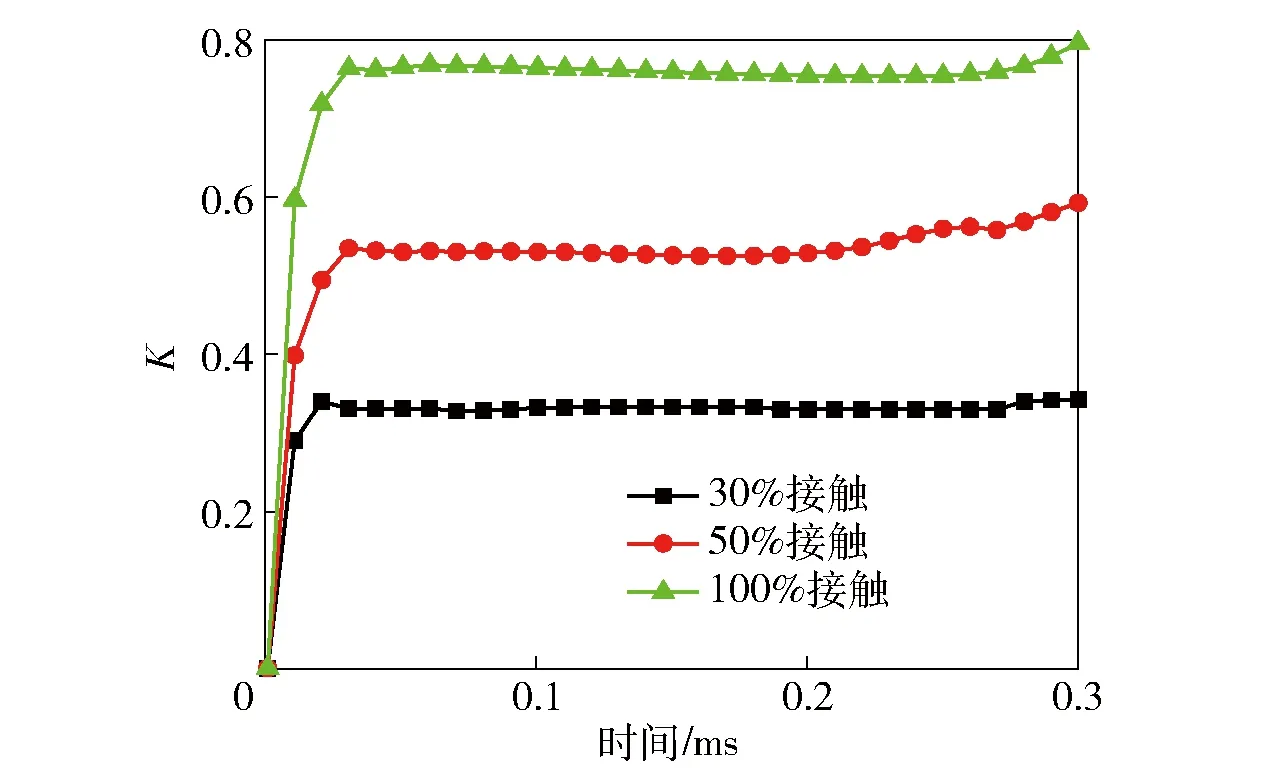
图12 电磁压力与电磁接触压力比值曲线Fig.12 Ratio of electromagnetic pressure to electromagnetic contact pressure

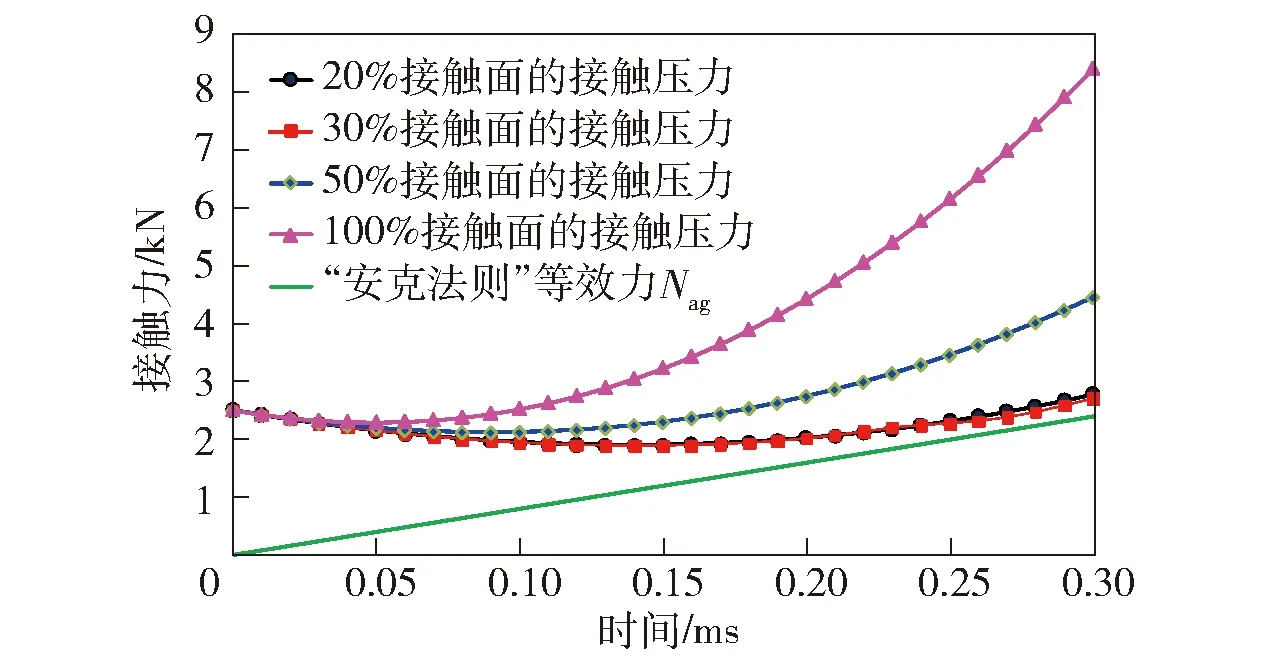
图13 接触压力曲线Fig.13 Contact force curves

由图12可知，K曲线在快速上升，并迅速稳定于0.75、0.54和0.33. 在电枢与轨道全接触情况下，电枢的电磁压力也只有75%作用在接触压力上。文献[2]中得到的结论是：“理论与试验结果较一致，表明电流通过电枢两翼接触面上压强较大的主要范围为其后半部分，且压强较大区域占电枢接触面长度的比例变化不大，约为1/2”。因此结合文献[2]中的计算结论，可得出枢轨良好接触的面积约占侧面积的30%～50%. 按A=30%计算，K的取值约为0.33.

从图13中可以看出，应用修正后的接触压力计算方法，随着枢轨接触面的增大，接触压力曲线均在Nag线之上，表明该方法能够有效地模拟电磁发射初期的枢轨接触压力。

3 发射试验验证

通过影响电磁发射起始阶段枢轨电接触性能的重要因素“枢轨接触面与接触压力”的计算与分析可知，枢轨良好的接触面约占侧面积的30%. 因此，选取A=30%接触的电枢，在小口径轨道炮优化平台进行多发试验，验证应用“安克法则”瞬态应用方法设计的电枢结构能够更好地实现起始段电接触性能。

3.1 轨道起始段损伤形貌表征枢轨接触状态

基于电磁轨道优化试验平台，选取不同结构的电枢(见图14)进行5发试验，试验条件如表1所示。试验中电枢尾翼后半部接触30%，多发试验后轨道起始段损伤形貌如图15所示。

图14 试验中使用的C形电枢Fig.14 C-shaped armatures for experiment

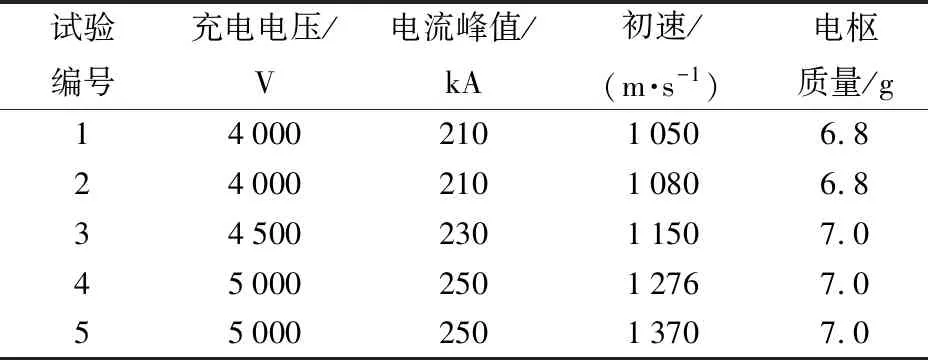
试验编号充电电压/V电流峰值/kA初速/(m·s-1)电枢质量/g1400021010506.82400021010806.83450023011507.04500025012767.05500025013707.0

图15 轨道起始段损伤形貌Fig.15 Damage morphology of initial section of rail

从图15中可见，应用该方法设计的30%接触的电枢在发射试验中，轨道起始阶段没有烧蚀引起的刨坑，实现了较好的起始段电接触性能。

3.2 优化试验平台的接触压力方法验证

选取第1发试验后的轨道扩张量数据，结合电枢过盈量可得出机械预压力，基于电枢的加速度、电流曲线、轨道的电感梯度可获得枢轨电磁接触压力。根据上述试验数据可得出起始段枢轨接触压力随时间变化曲线如图16所示，图17所示为枢轨30%接触条件下枢轨接触压力仿真计算结果。

图16 枢轨接触压力试验曲线Fig.16 Experimental curves of contact force

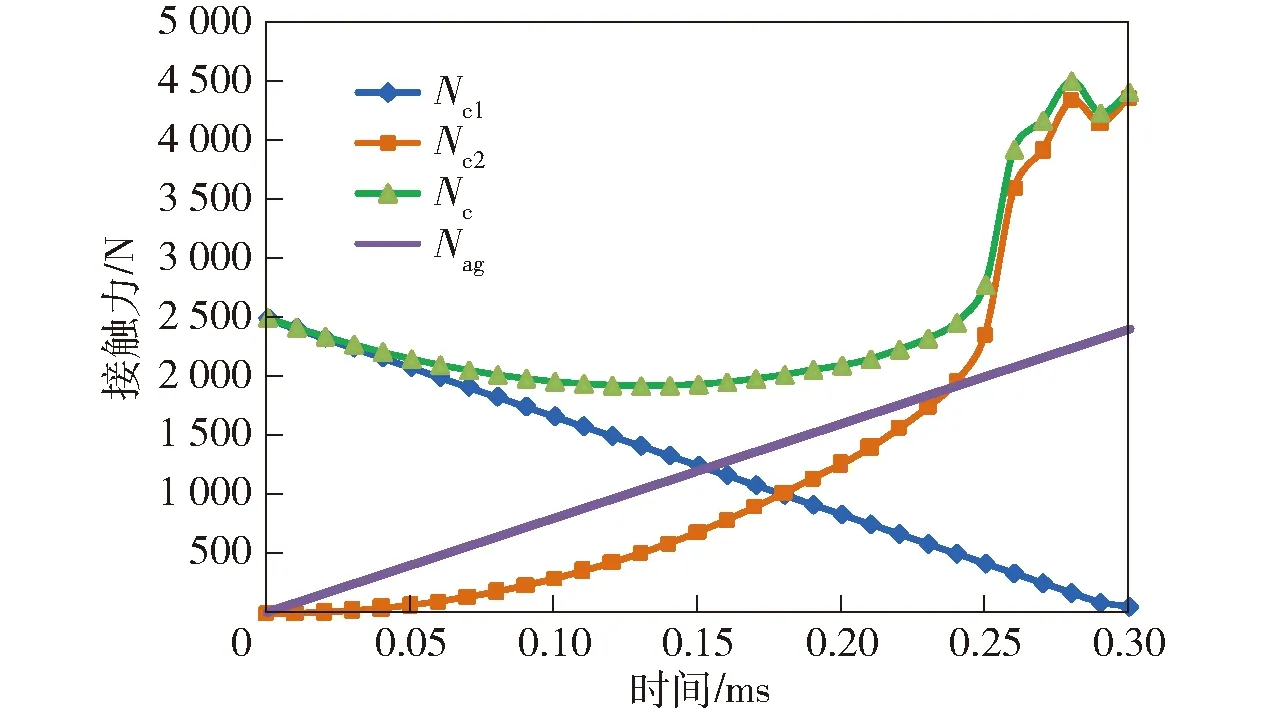
图17 枢轨接触压力仿真曲线Fig.17 Calculating curves of contact force

对比图16和图17可以看出，接触压力曲线变化趋势基本一致，均在“安克法则”等效力Nag线之上。表明“安克法则”瞬态应用方法能够较准确地模拟发射初始段枢轨之间的接触压力。

综上所述，通过调整枢轨接触面对电枢结构设计有着重要作用。采用“安克法则”瞬态应用方法计算枢轨接触压力，避免了枢轨失效的现象，有望实现更好的起始段电接触性能。

4 结论

本文利用电枢与轨道接触模型，从枢轨接触面和接触压力两方面对C型一体电枢结构进行了优化设计。研究了电枢接触面对电枢电磁特性的影响规律，提出了接触压力瞬态应用方法并进行了计算与试验验证，获得了枢轨接触压力曲线。得到主要结论如下：

1)枢轨接触面对电枢电磁特性影响较大，即在初始阶段电流通过电枢两翼接触面的主要范围为后半部分，为了保证电枢与轨道接触良好，电枢与轨道接触面位置为靠近电枢后半部分，且大小为30%～60%.

2)应用“安克法则”瞬态应用方法设计的电枢在发射起始段的接触压力曲线Nag之上，且与通过试验数据获得的接触压力曲线趋势基本一致，验证了该方法能够有效地模拟电磁发射初期的枢轨接触压力。

3)通过多发试验证明，基于“安克法则”瞬态方法设计的30%接触电枢，在多发试验后轨道起始段没有烧蚀引起的刨坑，实现了较好的起始段电接触性能。以上结论可供未来电枢设计参考。

本文的计算将电枢与轨道系统设置为相对静止，在高频涡流场中等效速度趋肤进行有限元计算极大地简化了运算，同时也使其对发射过程中的参考价值受到了一些影响。下一步的研究重点是计算电枢在动态条件下枢轨滑动电性能的研究。