固定鸭舵双旋弹动态稳定性分析
2019-11-05马国梁蔡红明常思江
马国梁,蔡红明,常思江
(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.南京理工大学 机械工程学院,江苏 南京 210094)
0 引言
常规弹药制导化的改造过程中,从总体设计角度出发,需要综合考虑作战性能和制造成本。弹道修正弹通过对常规弹药进行改进,加装弹道修正组件,在保证低成本的同时提高命中精度,受到国内外相关领域研究者的重视,先后出现了阻力修正弹、脉冲修正弹以及鸭舵修正弹[1]。随着鸭舵控制机构微型化技术的进步,鸭舵修正弹由于控制效率较高逐渐成为弹道修正弹的首选方案。双旋弹是近年来出现的一种新型弹道修正弹,由弹道修正组件和主弹体两部分组成,中间采用滚动轴承联接,在弹道飞行过程中,两部分以不同转速绕弹体纵轴旋转,其动力学特性分析[2]、导引及控制设计[3-4]得到国内外相关领域研究者的重视。
双旋弹修正机构往往安装在原来常规弹药的引信部位,考虑到尺寸及成本的严格限制,前体鸭舵往往是固定的,没有可动的舵面[5],只能与整个弹道修正引信(CCF)一起绕弹体纵轴旋转,因此可称为固定鸭舵双旋弹。Costello等[6]研究了双旋弹线性理论,考虑了前体、后体的相互作用力和力矩,分析了双旋弹的飞行稳定性。法德圣路易斯研究所对双旋弹风洞测试、动力学特性、飞行稳定性进行了长期研究[7-10]。王志刚等[11]采用多体动力学的凯恩方法建立了双旋火箭弹的动力学模型。许诺等利用角运动方程分析了固定鸭舵双旋弹的动力学特性[12],进一步研究了固定鸭舵双旋弹的动力学分岔特性[13],并基于周期平均概念提出了一种双旋弹的弹道修正控制方法[14]。郭致远等[15]结合电机执行机构的特性,进一步研究了固定鸭舵双旋火箭弹的周期控制策略。王钰等[16]采用等效控制力方法分析了双旋弹在侧向控制力作用下的弹丸落点位置变化规律。常思江等[17]对双旋弹鸭舵周期干扰引起的强迫运动进行了研究。Chang等论述了鸭舵控制和重力作用下双旋弹的动态响应[18],并分析了双旋弹的转速特性[19]。Liu等[20]研究了在固定鸭舵控制力作用下的弹道摆动问题。
双旋弹研制过程中,飞行稳定性是应该首要解决的理论问题。文献[21]针对舵偏角可调节情况分析了双旋弹的飞行稳定性,文献[6]的稳定性分析方法适用于前体自由旋转、不考虑鸭舵受控的情形,而文献[12,22]在分析双旋弹稳定性时假定CCF匀速旋转或者固定不动。从工程实际情况来看,考虑到控制律设计的多样性,在整个弹道飞行控制过程中,CCF的控制滚转角变化可能是任意时变的,这就需要应用条件更宽泛的稳定性分析方法。
通过分析固定鸭舵双旋弹的结构特点,本文将前体舵面滚转角看作控制输入量,研究滚转角任意变化时的飞行稳定性问题。根据固定鸭舵双旋弹的力方程组和力矩方程组得出角运动状态方程,选取二次Lyapunov函数分析角运动状态矩阵的稳定性。利用复数平方根计算方法得出了稳定因子的表达式,并结合界实引理提出了绝对稳定H∞范数的概念。研究结果表明:固定鸭舵双旋弹动态稳定的充分条件是同时满足稳定因子约束和绝对稳定H∞范数约束。最后分别通过仿真示例验证了固定鸭舵双旋弹动态稳定性判据的有效性。
1 动力学建模
1.1 前提假设
固定鸭舵双旋弹的CCF主要集中在引信部位,如图1所示。后体高速旋转时,前体舵面如果不加任何锁定力矩,仍会由于轴承摩擦力矩的影响以一定转速旋转。前体有两对舵面:舵面1和舵面3为减旋舵面,设计时有一定导转角,产生的导转力矩方向与轴承摩擦力矩方向相反,以降低后体高速转动对前体的影响;舵面2和舵面4为鸭舵,用于产生舵面升力,与制导弹药常见的舵面机构不同,舵面2和舵面4的舵偏角是固定的,即所谓的固定鸭舵,只能改变整个前体组件的控制滚转角,使得鸭舵升力方向发生变化,以改变飞行弹道。为便于分析,只考虑影响较大的气动力与力矩,通过气动计算及实验分析可以对气动系数进行估计。
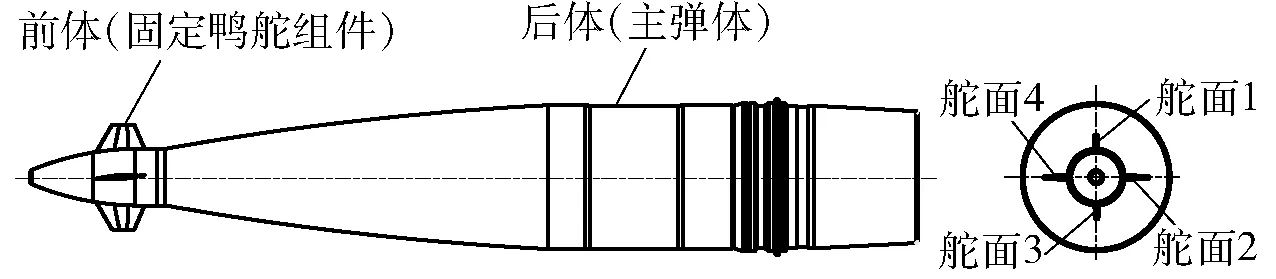
图1 固定鸭舵双旋弹Fig.1 Fixed canard dual-spin projectile
1.2 坐标系定义
1.2.1 地面发射坐标系
地面发射坐标系与地球表面固连,坐标原点定义在炮口断面中心,x轴沿水平线指向射击方向,y轴在水平面内,垂直射击面向右(由弹底部前视),z轴按右手法则定义指向下方。为简化研究,将地面发射坐标系近似为惯性坐标系。
1.2.2 弹体固定面坐标系

1.2.3 前体坐标系
坐标原点O位于全弹质心。xb轴与弹体纵轴重合指向弹头,yb轴垂直于前体纵向对称面指向右侧,zb轴按右手法则定义指向下方。前体坐标系由BFP坐标系旋转滚转角φF得到,根据固定鸭舵双旋弹的特点,φF看作是控制量。
1.3 气动力及气动力矩
为简化问题,结合双旋弹气动外形特点,主要考虑影响较大的气动力和气动力矩。忽略马格努斯力,对于舵面部分,只考虑舵面引起的升力和俯仰力矩。
1.3.1 阻力

1.3.2 弹体升力
弹体升力向量表示为
(1)
式中:xu为弹体纵轴方向上的单位向量;i为飞行速度方向上的单位向量;CLα为弹体升力系数。
1.3.3 舵面升力
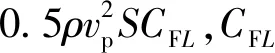
1.3.4 弹体俯仰力矩
外弹道学中习惯称为静力矩或者翻转力矩,弹体俯仰力矩向量为
(2)
式中:d为参考长度,这里取弹的直径为参考长度;CMα为弹体俯仰力矩系数。
1.3.5 俯仰阻尼力矩
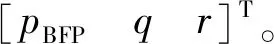
(3)
式中:CMq为俯仰阻尼力矩系数。
俯仰阻尼力矩在外弹道学中习惯称为赤道阻尼力矩。
1.3.6 弹体滚转阻尼力矩
滚转阻尼力矩在外弹道学中习惯称为极阻尼力矩,滚转阻尼力矩方向指向弹体纵轴,大小为
(4)
式中:p为弹体转速;Clp为滚转阻尼力矩系数。
1.3.7 马格努斯力矩
马格努斯力矩向量方向指向弹体纵轴,表示为
(5)
式中:CMpα为马格努斯力矩系数。
1.3.8 舵面俯仰力矩
1.4 其他力和其他力矩
整个弹丸在飞行过程中质量不变,忽略重力常数随弹道高度的变化,认为弹丸飞行过程中受到恒定的重力作用。
研究固定鸭舵双旋弹的角运动变化规律时,前体和后体相互作用的摩擦力矩客观存在,而且根据轴承结构的特点,摩擦力矩主要包括黏滞摩擦力矩和滚动摩擦力矩。本文将前体舵面滚转角φF看作控制量,重点讨论固定鸭舵双旋弹的飞行稳定性问题,因此暂不分析摩擦力矩的具体影响。
1.5 动力学模型
固定鸭舵双旋弹的动力学模型不同于传统的6自由度外弹道模型,一些学者在研究双旋弹动力学特性时,常常将弹丸前体和后体的转速都看作独立运动变量,相对于传统的6自由度外弹道模型增加了1个前体转速变量,因此建立的是7自由度外弹道模型[6,17]。由于固定鸭舵双旋弹的舵偏角固定,对弹道进行修正时只能通过改变前体滚转角φF来实现,在此情况下前体转速不再是独立运动变量,受到滚转角控制量φF的限制。本文主要研究固定鸭舵双旋弹前体受控条件下的飞行稳定性,因此没有采用文献[6,17]的7自由度模型,而是采用文献[9]得到的固定鸭舵双旋弹6自由度模型。根据BFP坐标系的定义可以得出pBFP=-rtanθ,由牛顿第二定律,经推导可得双旋弹力学方程组为
(6)
(7)
(8)
式中:u、v、w为飞行速度向量在BFP坐标系中的3轴分量;m为全弹质量;g为重力加速度常数。 进一步根据动量矩定理,经推导可得双旋弹力矩方程组为
(9)
(10)
(11)
式中:Ix为轴向转动惯量;Iy为横向转动惯量。
2 稳定性分析
2.1 线性化状态方程
根据BFP坐标系的3轴速度分量计算弹体攻角α和侧滑角β,有以下关系式成立:
u=vpcosαcosβ,
(12)
v=vpsinβ,
(13)
w=vpsinαcosβ.
(14)
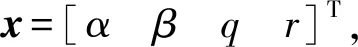
αF≈αcosφF+βsinφF.
(15)
将(12)式~(15)式代入力方程组和力矩方程组,进行线性化处理,将得到以x为变量的状态方程,其中气动系数CFL0、CFM0出现在状态方程的非齐次项中。考虑到动态稳定性讨论问题的特点,只保留状态方程的齐次项,得到固定鸭舵双旋弹角运动状态空间模型为
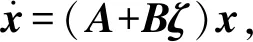
(16)
式中:A=

可以看出,角运动状态矩阵可以分解为两项相加的形式,一项为A,另一项为Bζ.A只与弹体部分的气动系数及弹道运动参数有关,而弹体部分气动系数与原来无控弹的气动系数数值接近,因此为便于叙述,将A称为无控状态矩阵。B与前体鸭舵的气动导数有关,ζ与前体鸭舵的滚转角数值有关,相应地将Bζ称为有控状态矩阵。
2.2 固定鸭舵双旋弹绝对稳定性判据
在固定鸭舵双旋弹的研制过程中,需要根据弹道偏差改变前体舵面滚转角φF,即控制量φF将是变化的。如果固定鸭舵双旋弹在φF任意变化时都是绝对稳定的,将会给φF的控制律设计带来很大方便,为此提出固定鸭舵双旋弹绝对稳定性判据,表述如下:
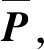
(17)
式中:I为维数适当的单位矩阵。
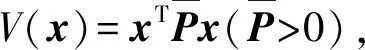
(18)
由于始终满足
(19)
展开(19)式,整理可得
(20)
计算可知
则有
(21)
由定理1可以看出,固定鸭舵双旋弹的动态稳定性问题可以通过求解一个Riccati不等式(17)式来判别。根据Schur引理[23],(17)式等价于如下矩阵不等式成立:
(22)
对定理1的结果可以作进一步转化,为此引入由Scherer改进的界实引理[24]:
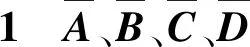
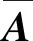
(23)
式中:s为Laplace算子。
(24)
定理2对于固定鸭舵双旋弹,若飞行状态矩阵A是稳定的且‖(sI-A)-1B‖∞<1,则在前体舵面控制滚转角φF任意变化的情况下,固定鸭舵双旋弹都绝对是动态稳定的。
根据飞行力学理论可知,当增大前体鸭舵的升力系数导数时,对应的俯仰力矩导数会相应增大,而由B矩阵的表达式可知,这会使‖(sI-A)-1B‖∞的数值增大,就越不容易满足绝对稳定判据,对飞行稳定性带来不利影响。
2.3 稳定因子和绝对稳定H∞范数
由定理2可知,固定鸭舵双旋弹的绝对稳定条件要求A是稳定阵‖(sI-A)-1B‖∞<1,根据线性系统稳定性理论可知,如果状态矩阵A的所有特征根具有负实部,则A是稳定的。
通过符号化求解,可得A的4个特征根为
(25)
(26)
(27)
(28)
式中:a=4M+H2-P2+4T(T-H);b=2P(2T-H+2K)。
根据复数的平方根计算方法[25],可以进一步对特征根的形式进行整理:当b≥0时,4个特征根可以表示为如下两对共轭复根:
(29)
(30)
当b<0时,4个特征根可以表示为如下两对共轭复根:
(31)
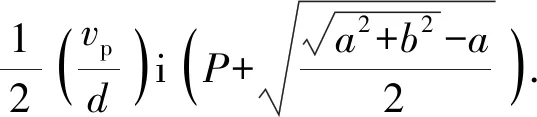
(32)
两对共轭复根的实部取值也不同,分别为
(33)
(34)
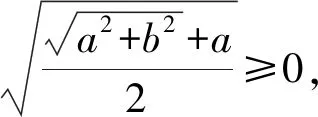
定理3在前体舵面控制滚转角φF任意变化的情况下,固定鸭舵双旋弹绝对动态稳定的条件为:
1) 稳定因子λs<0;
2)绝对稳定H∞范数满足Sa<1.
定理3可用于判断具有固定鸭舵结构的尾翼稳定弹或者旋转稳定弹。固定鸭舵双旋弹的绝对稳定条件在形式上比无控弹稳定条件更加保守,无控状态矩阵A稳定不一定能保证固定鸭舵双旋弹的绝对稳定性,而固定鸭舵双旋弹如果是绝对动态稳定的,则无控状态矩阵A一定是稳定的。
3 仿真分析
采用某固定鸭舵155 mm榴弹的有关数据进行外弹道仿真分析,仿真用到的物理参数如表1所示,气动力系数如表2所示,气动力矩系数如表3所示。

表1 物理参数
仿真初始条件为:初速930 m/s,初始转速1 885 rad/s,俯仰角初值θ0=45°,其余状态初值为0,采用炮兵标准气象条件进行仿真计算。
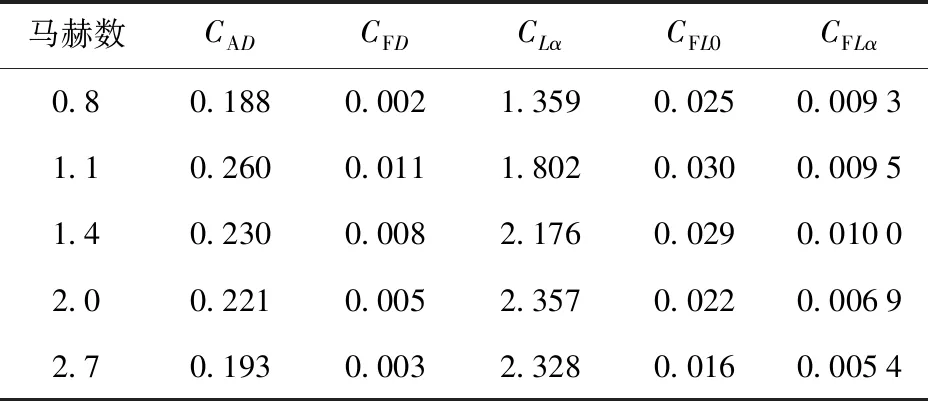
表2 气动力系数
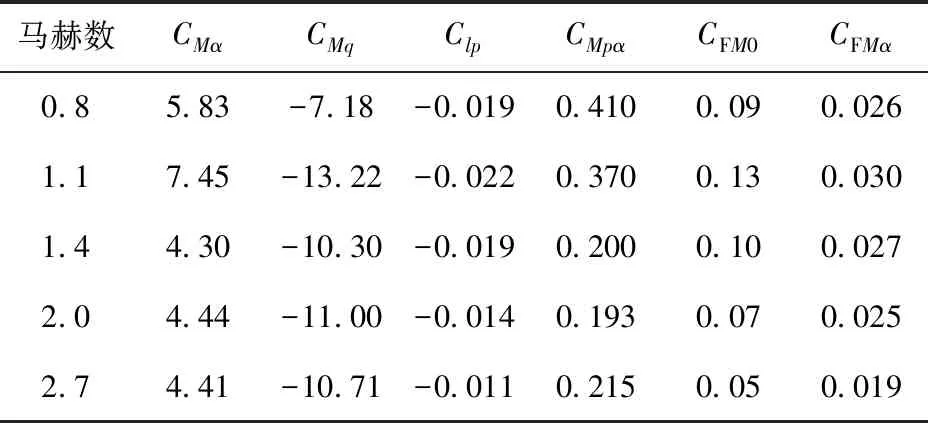
表3 气动力矩系数
为了验证绝对稳定性分析方法的有效性,生成前体鸭舵控制滚转角的随机指令曲线如图2所示。外弹道仿真计算表明,全弹道稳定因子λs的变化曲线如图3所示,可以看出始终满足λs<0,意味着无控状态矩阵A是稳定的。全弹道的绝对稳定H∞范数Sa变化曲线如图4所示,可以看出始终满足Sa<1. 同时满足λs<0及Sa<1,意味着固定鸭舵双旋弹在控制滚转角φF任意变化情况下都是绝对动态稳定的。
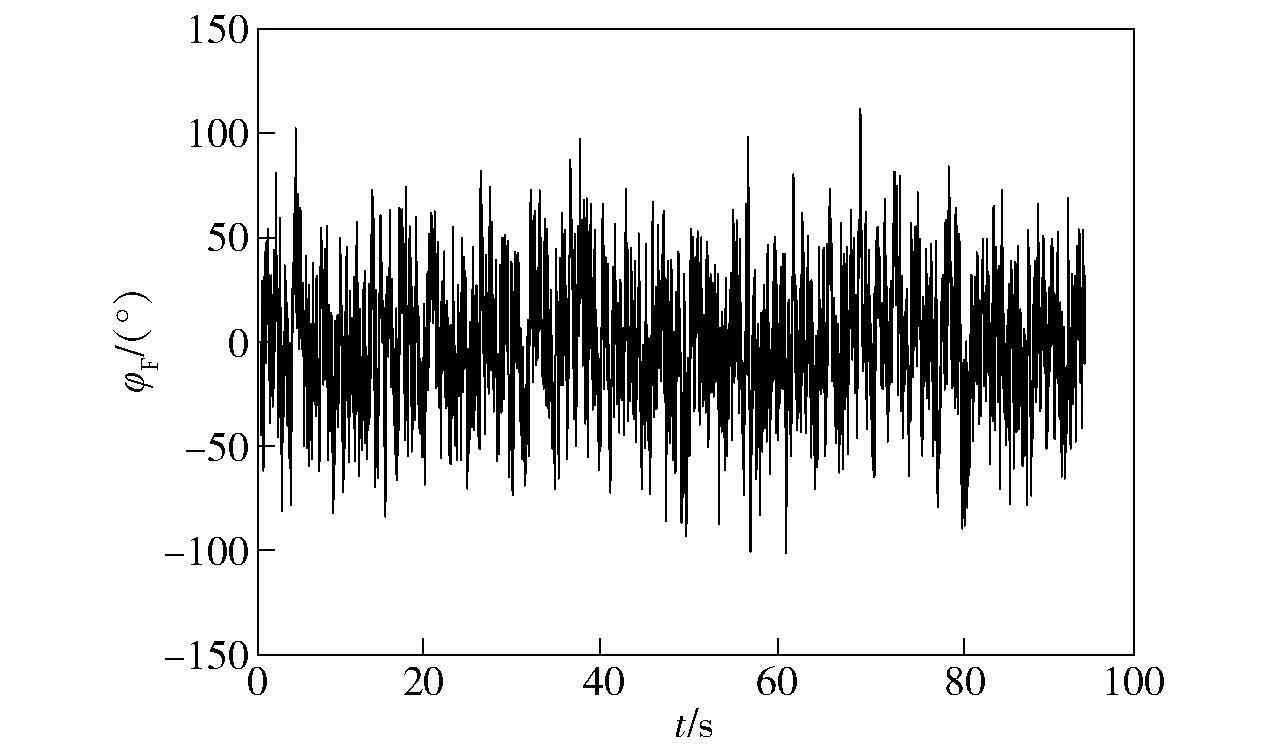
图2 鸭舵滚转角曲线Fig.2 Curve of canard roll angle

图3 稳定因子曲线Fig.3 Curve of stability factor
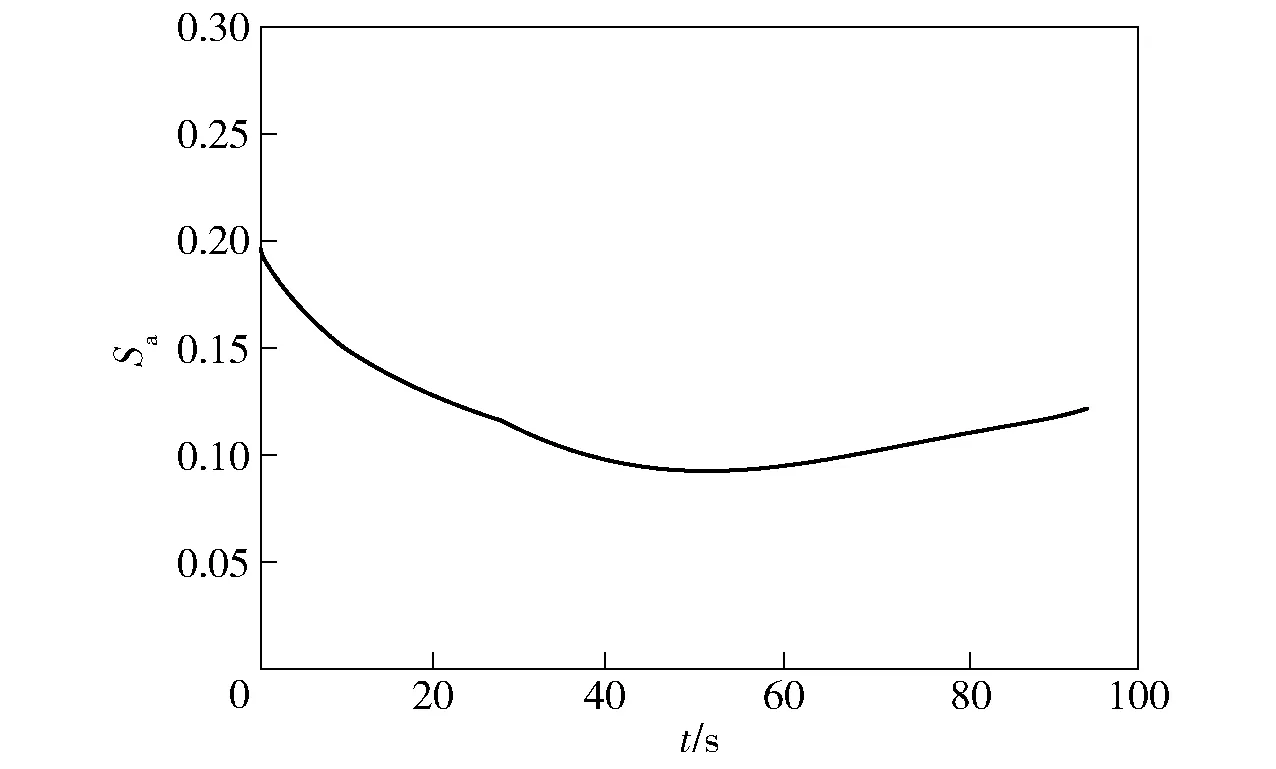
图4 绝对稳定H∞范数曲线Fig.4 Curve of H∞ norm of absolute stability
绘制出固定鸭舵双旋弹的攻角侧滑角变化曲线如图5所示,可见在固定鸭舵控制滚转角随机变化的作用下,弹丸始终是动态稳定的。
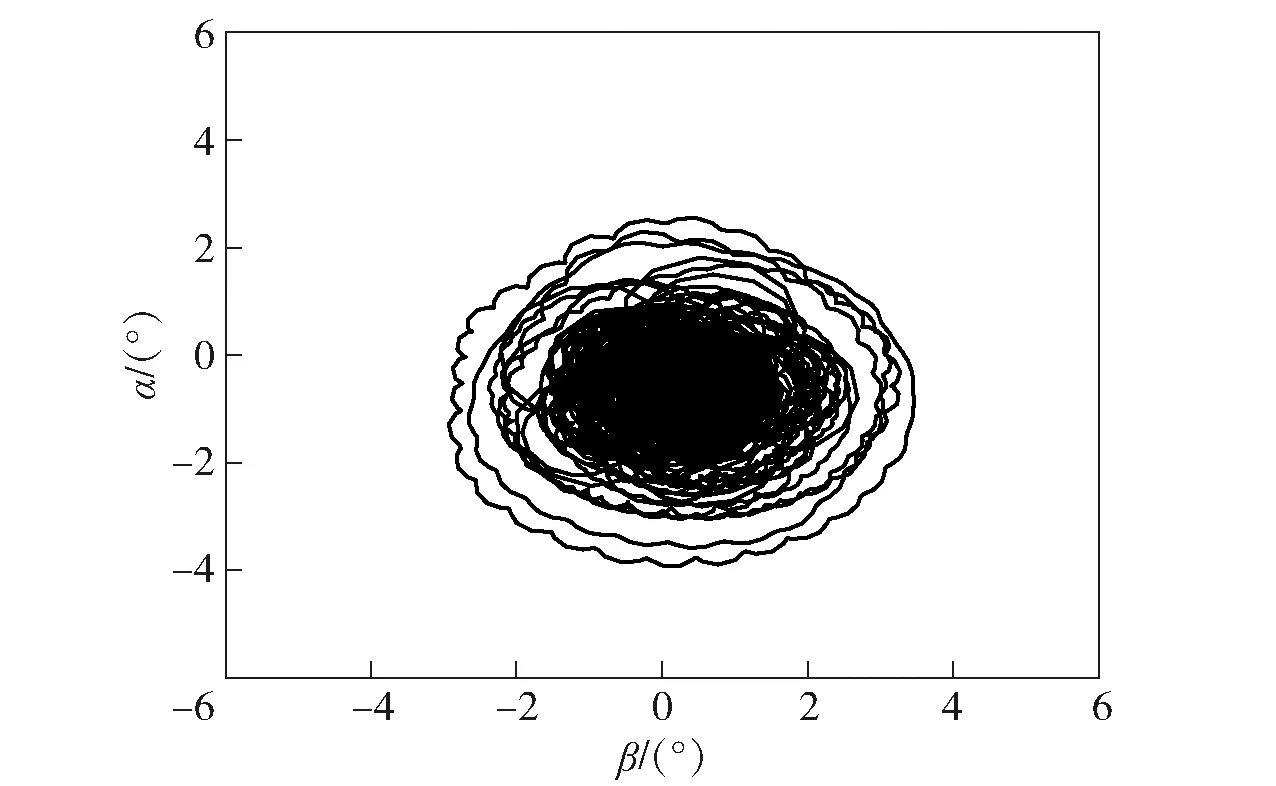
图5 固定鸭舵双旋弹攻角- 侧滑角曲线Fig.5 Attack angle-slide angle curve of fixed canard dual-spin projectile
靶场的多次试验结果表明,该双旋弹在鸭舵滚转角固定(φF为0°、90°、180°、-90°)和变化情况下,飞行过程都是动态稳定的,也进一步验证了以上分析结论。
4 结论
本文建立了固定鸭舵双旋弹在前体滚转角控制作用下的6自由度外弹道模型,研究了滚转角控制量任意变化时的动态稳定性问题。采用状态空间模型及Lyaounov方法进行分析,最终给出了固定鸭舵双旋弹的绝对稳定判据。所得主要结论如下:
1) 在固定鸭舵控制滚转角任意时变的条件下,固定鸭舵双旋弹的绝对稳定问题可以通过判断1个Riccati形式的线性矩阵不等式是否成立来解决。
2) 要想充分保证固定鸭舵双旋弹的动态稳定性,需要同时满足稳定因子约束和绝对稳定H∞范数约束。
3) 固定鸭舵的升力系数导数数值增大时,会更不容易满足绝对稳定判据。
4) 本文的绝对稳定性判据适用于鸭舵滚转角任意时变的所有情况,鸭舵滚转角保持常值时仍可使用,不过会有一定保守性。鸭舵的气动系数CFL0、CFM0虽然没有影响动态稳定性,但对追随稳定性会产生影响,这都有待进一步研究。
