推力和阻力作用下柔性自旋飞行器稳定性分析

潘成龙，荣吉利，徐天富，项大林

(1.北京理工大学 宇航学院，北京 100081； 2.中国兵器工业集团航空弹药研究院，黑龙江 哈尔滨 150030；3.北京宇航系统工程研究所，北京 100076)

0 引言

大长径比自旋飞行器在飞行中，受到空气动力、发动机推力、控制力等作用，会发生弹体弹性变形和振动，影响飞行器稳定性和飞行性能。高速度和高机动，使得自旋飞行器在推力作用下的稳定性问题日益突出。在研究自旋飞行器时，一般采用梁模型，很多学者对推力作用下的梁模型进行了研究。Beal[1]采用均匀梁模型，在定常推力和脉动推力作用下，分析了推力和长径比对系统振动频率和系统稳定性的影响。Wu[2]采用限元方法，分析了带有集中质量的非均匀梁模型，结果表明集中质量对临界推力值和动稳定域有相当大的影响，随动推力作用使原刚体模态转变成为最小的非零频率。宋健[3]在推力和阻力作用下建立横向运动方程，得到了均匀截面飞行器临界推力的解析解。文献[4-5]采用非均匀梁模型，分析了随动推力对颤振临界速度、稳定性及模态振型的影响。张雷等[6]考虑气动耦合项，对推力作用下细长导弹的横向弯曲振动进行了数学建模，讨论了由气动弹性引起的振动模态频率以及临界推力的变化情况。Wu等[7]采用1阶活塞理论计算气动力，分析了柔性弹箭的颤振特性。全景阁等[8]使用有限元方法分析了大长细比导弹在轴向载荷作用下的结构刚度特性。

以上研究都是基于Euler梁理论，与Euler梁相比，Timoshenko梁考虑了转动惯量和剪切效应。陈红永等[9]通过解析法和微分求积法(DQM)求解了梁的振动特性，分析了轴向压力和运动效应以及轴向力导数和运动加速度对梁固有特性的影响，并对临界载荷、临界速度等的影响因素进行了比较研究。陈强等[10]基于动力刚度矩阵法分析了轴向变速运动弯曲梁固有频率随着弯曲梁轴向运动速度、加速度、轴向受力、边界条件的变化规律。王乐等[11]采用分离变量法求解了自由边界轴力作用下Timoshenko梁的自由振动方程。

考虑自旋时，飞行器稳定性也会受到影响。Zhu等[12]采用Timoshenko旋转梁理论，建立弯曲、扭转、轴向三维耦合非线性动力学方程，分析了变推力作用下系统质量偏心因素对自旋飞行器系统动力特性的影响。荣吉利等[13-15]将转子动力学应用于外弹道学，采用有限单元法建立了随动推力作用下柔性自旋飞行器横向振动方程，分析了转速和推力对系统稳定性的影响。Xu等[16]基于Timoshenko梁模型，研究了随动推力对柔性自旋飞行器气动弹性稳定性的影响。文献[13-16]采用的是平均轴系，在该坐标系下系统的动量为0 kg·m/s，动量矩为0 kg·m2/s，然而其限制条件很难在真实情况满足[17]，针对这些不足，郭东等[17]提出瞬态坐标系，陈尔康等[18]将瞬态坐标系应用于旋转导弹动力学建模。

本文将自旋飞行器简化为Timoshenko旋转梁，考虑陀螺效应和剪切效应，运用转子动力学和有限元思想，采用假设模态法和Lagrange方程，在瞬态坐标系下推导出推力和阻力作用下柔性自旋飞行器横向振动方程。分别从转速、推力和阻力3个方面分析了柔性自旋飞行器在轴向力作用下的稳定性，为柔性自旋飞行器研究提供了理论参考。

1 柔性弹箭动力学方程

1.1 动能、势能和外力功

针对平均轴系法存在的不足，瞬态坐标法具有固定的坐标轴指向，能够描述弹性变形对质心位置的影响，同时不同物理量能够在同一坐标系中描述。

如图1所示，建立准弹体坐标系Oxyz、瞬态坐标系Obxbybzb和微元坐标系O′ξηζ. 准弹体坐标系原点O位于未变形飞行器质心，瞬态坐标系原点Ob位于飞行器质心，两坐标系坐标轴指向相同。忽略轴向变形，图1中：R为轴段微元在瞬态坐标系下的位置矢量，R′为轴段微元在准弹体坐标系下的位置矢量，x0为轴段微元在准弹体坐标系下的轴向位置矢量，ΔC为飞行器质心的位置矢量，u为轴段微元中心相对准弹体坐标系的弹性变形矢量，P为随动推力，Ω为自旋转速。

图1 弹体模型图Fig.1 Flight vehicle model

在准弹体坐标系下，R′和ΔC的表达式为

R′=x0+u，

(1)

(2)

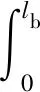
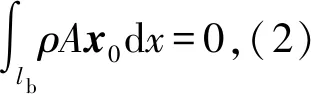
(3)

则

(4)

由(4)式知，轴段微元位置矢量在准弹体坐标系和瞬态坐标系下，相差矢量ΔC.

在准弹体坐标系下，x0和u分别为

(5)

(6)

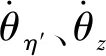
图2 坐标系转换Fig.2 Transformational relation between the coordinate systems

准弹体坐标系Oxyz和微元坐标系O′ξηζ绕3个坐标系的转换矩阵为

(7)

在微元坐标系下，轴段微元角速度[19]表示为

(8)

系统的动能可以表示为

(9)

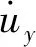
由于弹性变形为小变形，近似取cosθη′≈1和sinθη′≈θη′≈θy，将(8)式代入(9)式，得

(10)

考虑剪切影响，系统的弹性势能为

(11)

式中：EI为弯曲刚度；κGA为剪切刚度；上标符号“′”表示变量对x的偏导数。

随动推力作的功[13]为

(12)

式中：上标符号“‴”表示变量对x的3阶偏导数；PN为轴向力，

(13)

随动推力非保守部分作的虚功为

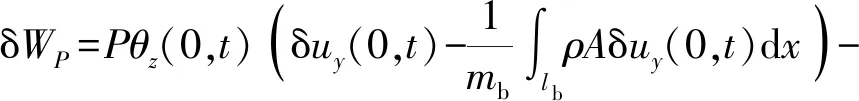
(14)

飞行器的轴向气动力主要有头部、尾部和底部波阻、侧面摩擦阻力等，这里将轴向气动力简化成头部集中阻力，集中阻力非保守部分作的虚功为[19]

δWFD=FDθy(xD,t)δuz(xD,t)-

(15)

式中：xD为头部集中阻力作用位置。

1.2 振动方程

用有限元方法，将弹体模型沿轴向进行离散，划分为n个梁单元。采用Timoshenko梁单元对横向位移和转角插值，即

(16)

式中：Φ和Ψ分别为位移和转角插值函数矩阵；ηy和ηz分别为y轴方向和z轴方向的广义坐标。

非保守系统Lagrange方程的形式为

(17)

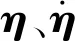
(18)

式中：M、G和K分别为系统的质量矩阵、回转矩阵和弹性刚度矩阵；KPN为轴向力保守部分得到的刚度矩阵；KP和KFD分别推力和阻力非保守部分得到的刚度矩阵；Qy和Qz分别为y轴方向和z轴方向的广义力。矩阵和向量中的元素分别为

(19)

(20)

(21)

(22)

(23)

(24)

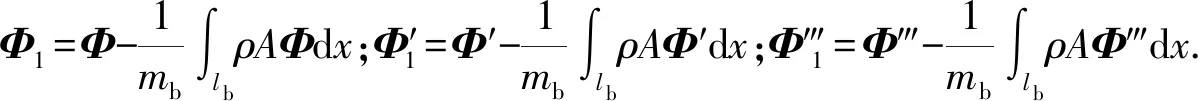
2 稳定性分析

将(18)式简化为

(25)

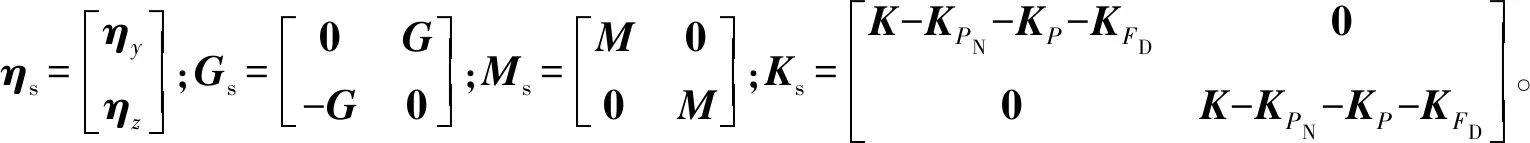
将(25)式写成状态方程形式：

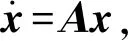
(26)

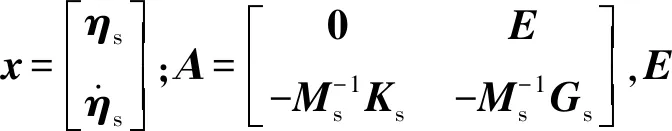
采用文献[5,7]中的方法，根据李雅普诺夫稳定性理论，来判断系统的稳定性。将系统稳定性分析转化为求解状态方程中矩阵Α的特征值问题。λi为非对称矩阵Α特征值，是复数，进动频率ωi=Im (λi)，模态阻尼为λi实部，i为阶数。

对参数无量纲化[15,19]：

(27)

式中：ω为系统基频。

以长径比为25.3的等截面细长回转梁模型作为仿真模型，整体分为5段，推力作用在轴段1的左端，初始时刻相关参数如表1所示，表中l为轴段长度。

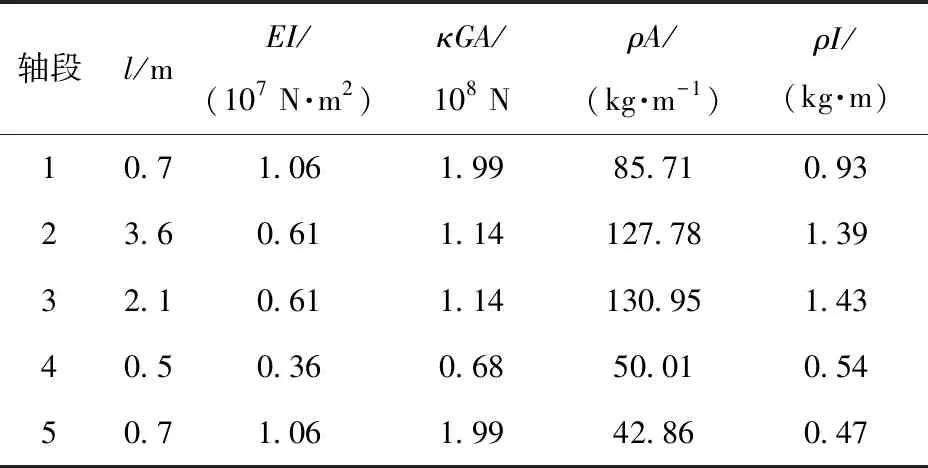
表1 梁轴模型参数

2.1 平均轴系下稳定性分析

图3 不同阻力下特征值Fig.3 Variation of eigenvalue with thrust under different drag loads

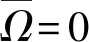
图4所示为转速对飞行器稳定性影响。由图4(a)知，α=0.2下，考虑旋转时，由于陀螺效应影响，正、反进动频率(由于反进动频率为负，这里取反进动绝对值进行分析)呈分离趋势，1阶反进动频率与刚体模态频率在P=0.8Pcr0时合并，P=1.0Pcr0时分离，1阶反进动频率增大并与2阶正进动频率合并，1阶正进动频率与2阶反进动频率在P=0.94Pcr0时合并。

图4 不同转速和不同阻力特征值变化Fig.4 Variation of eigenvalue with thrust under different drag loads and spinning speeds

由图4(b)知，在(0.8Pcr0，1.0Pcr0)区间，虚部为正数，发生动态失稳，临界推力降低，失稳区域变大，引起刚性运动和弹性振动耦合振动。

当α=1.0时，由图4(c)和图4(d)知，1阶反进动频率与刚体模态频率发生耦合，2阶正进动频率逐渐减小，在(0.43Pcr0，0.76Pcr0)区间，模态频率变为非零，静态失稳变成动态失稳，静态失稳推力变为动态失稳推力，失稳区域变大。

图5所示为阻力变化对临界推力的影响，图中Pcr为临界推力。由图5可见，随着阻力的增大，临界推力先缓慢变小，直线下降后逐渐变小。不考虑转速时，随阻力增大先发生动态失稳，在α1点，动态失稳变为静态失稳，动态临界推力变为静态失稳推力；考虑转速时，随转速增大，临界推力逐渐减小，当α>0.6时，转速对临界推力影响很小，转速使刚体模态频率与1阶反进动频率在α2和α3点合并，发生动态失稳。

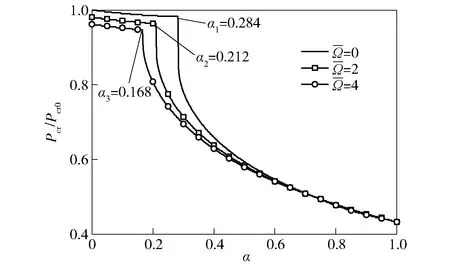
图5 临界推力变化Fig.5 Changing curves of critical thrust

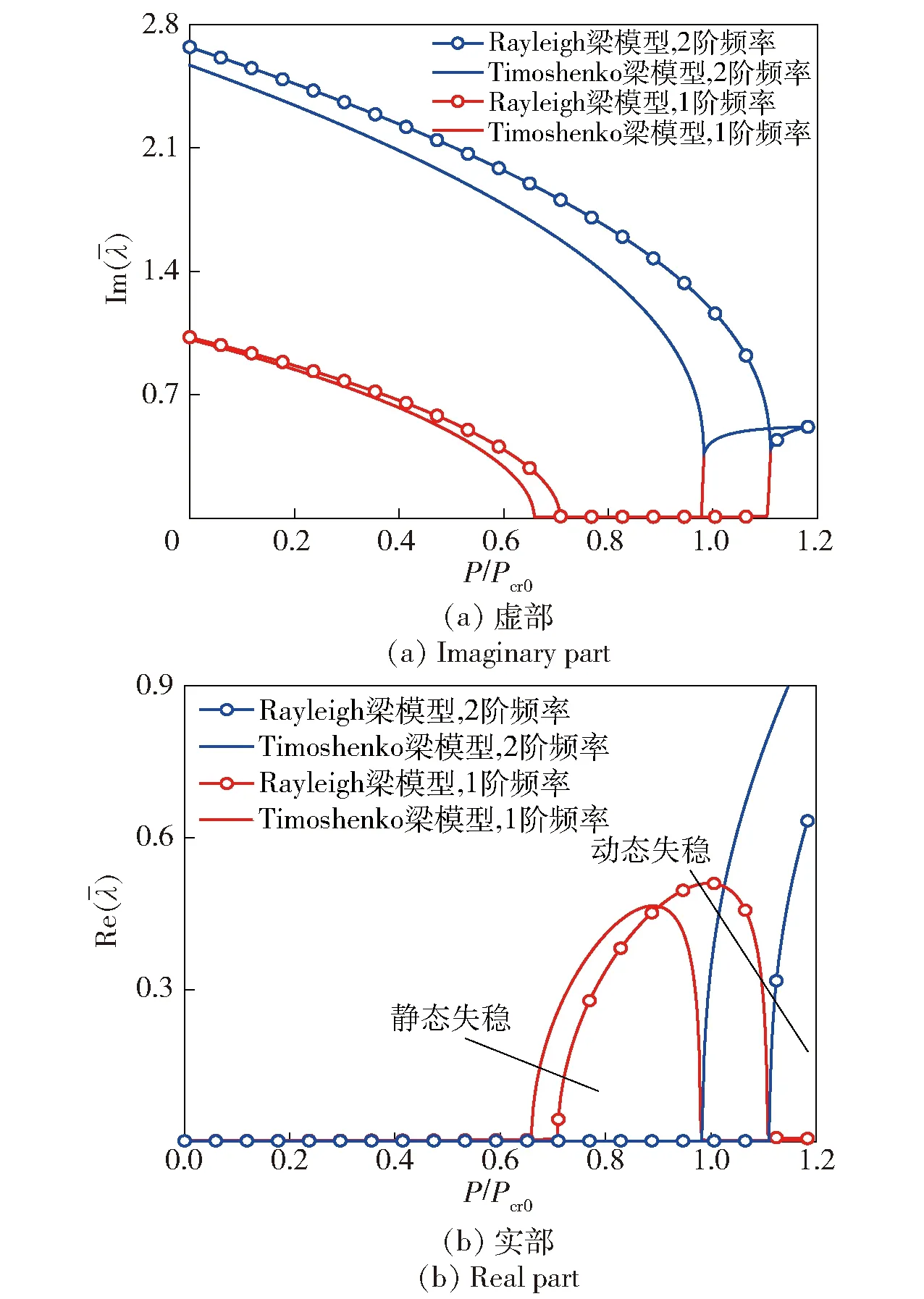
图6 不同梁模型特征值变化Fig.6 Variation of eigenvalue with thrust for different beams

图6所示为推力和阻力作用下不同梁模型稳定性的影响。将Timoshenko和Rayleigh梁模型在α=0.4时作对比分析，Timoshenko梁频率和静态失稳推力小于Rayleigh梁模型，对比1阶频率，剪切效应对2阶频率影响更大，剪切效应降低系统的稳定性。

当α=0和α=1.0时，计算3种均匀梁模型的临界推力，结果如表2所示。对比表2中的数据发现，转动惯量和剪切效应对临界推力都有影响，与转动惯量相比，剪切效应对临界推力影响更大。

2.2 平均轴系和瞬态坐标系模型对比

图7所示为转速对飞行器稳定性影响。由图7可见，与平均轴系模型相同，自旋转速能够使1阶、2阶正反进动频率呈分离趋势，对刚体模态频率影响不大。

表2 临界推力

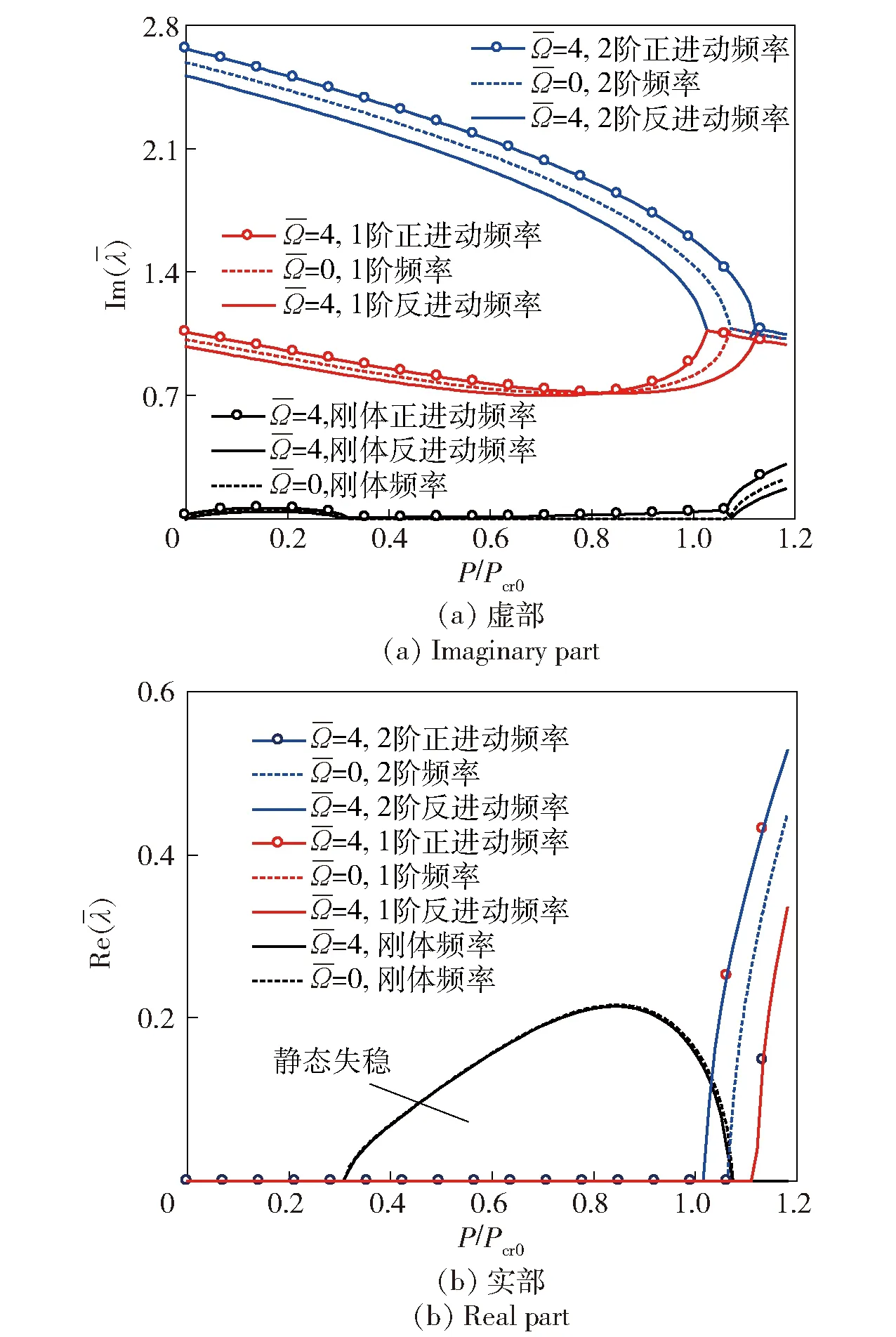
图7 瞬态坐标系中不用转速特征值变化Fig.7 Variation of eigenvalue with thrust in the transient coordinate system at different spinning speeds

将平均轴系模型和瞬态坐标系模型进行仿真，结果如图8～图10所示。

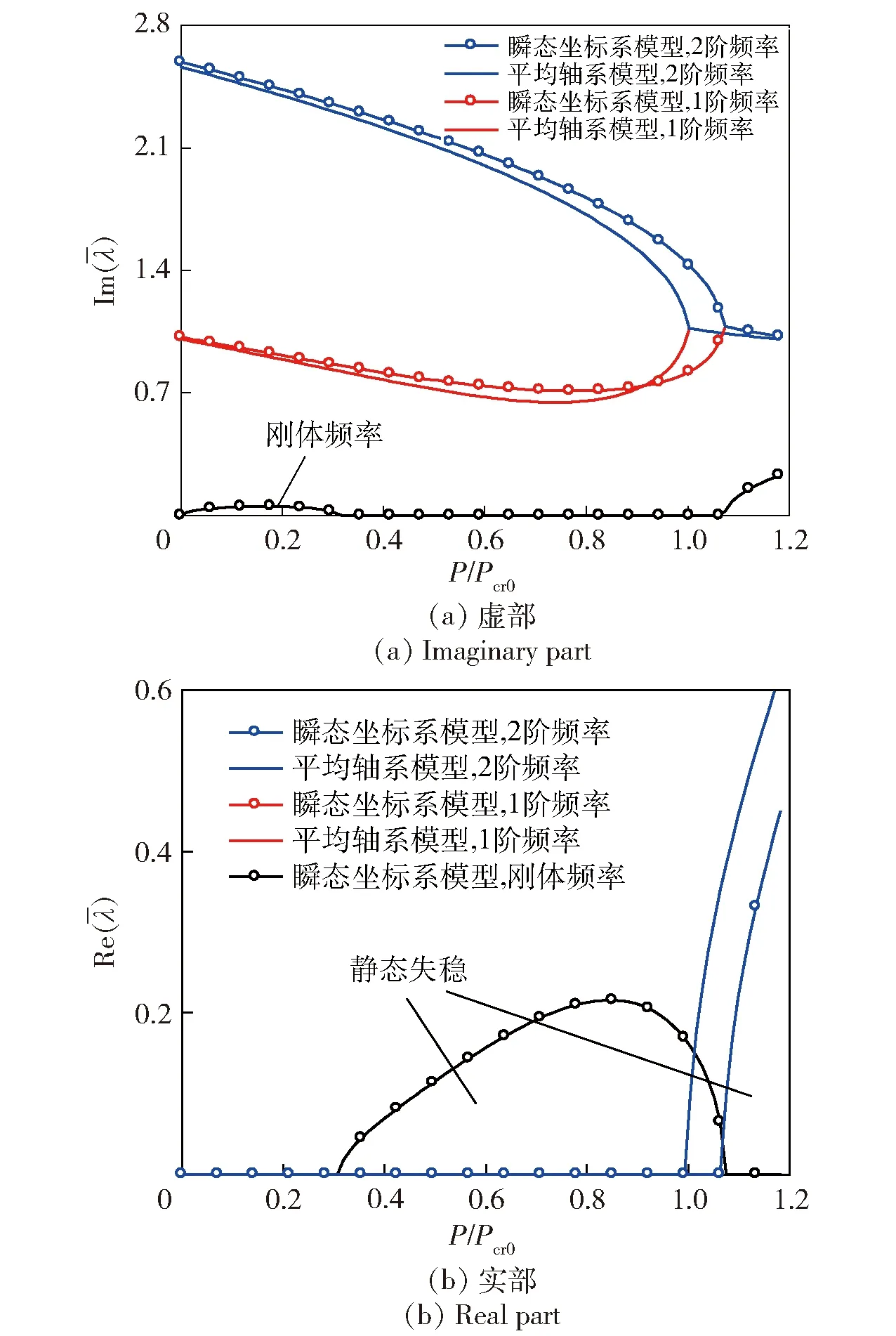
图8 不同坐标系模型特征值变化Fig.8 Variation of eigenvalue with thrust in different coordinate systems

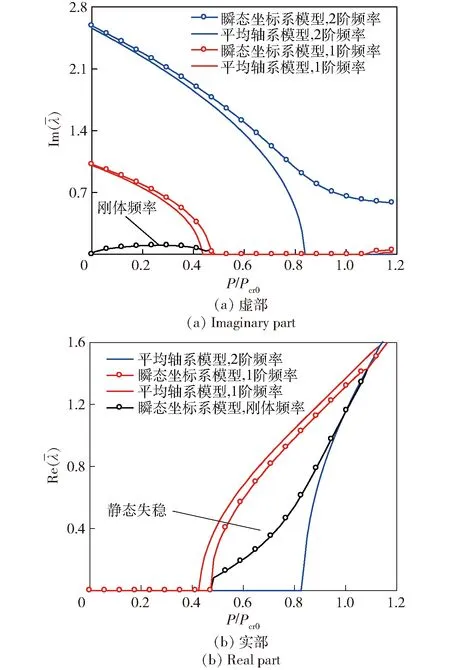
图9 阻力作用下不同坐标系模型特征值变化Fig.9 Variation of eigenvalue with thrust in different coordinate systems under drag load

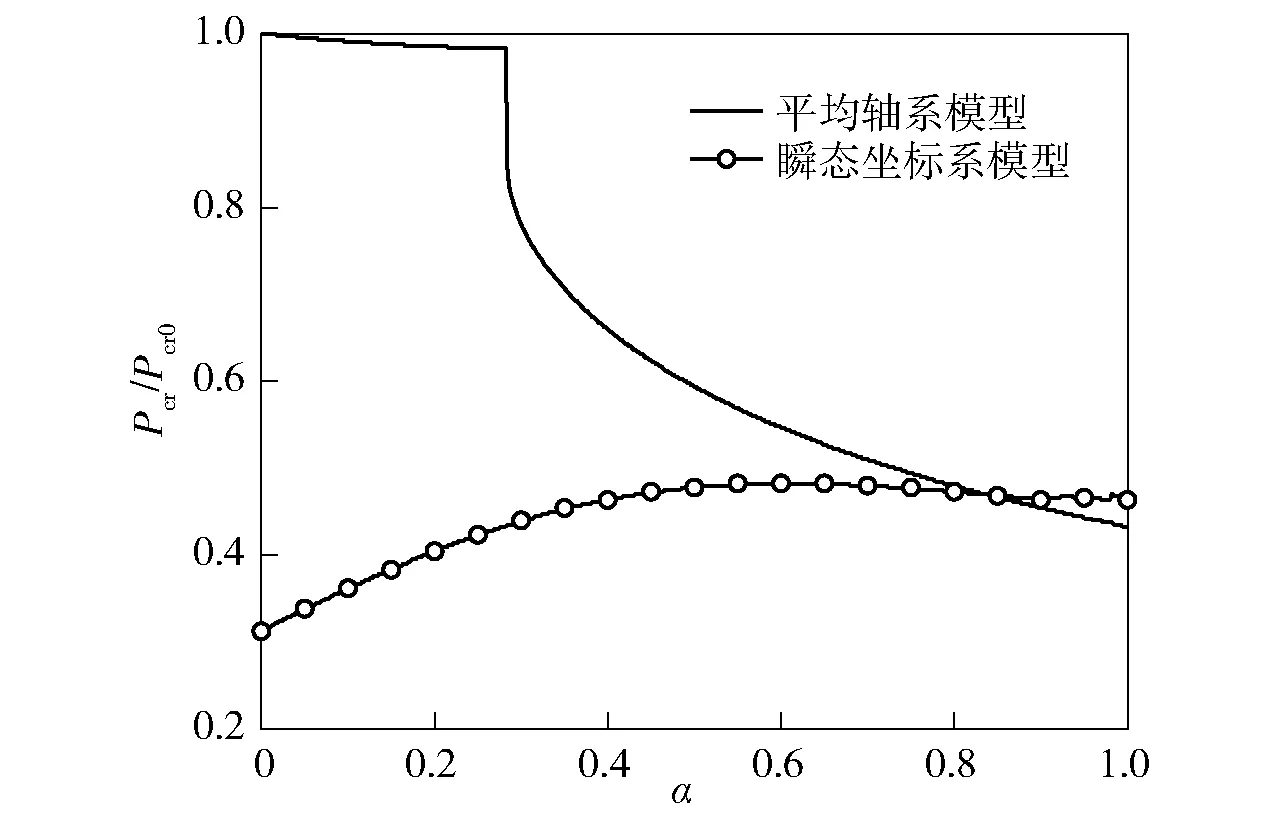
图10 不同模型临界推力变化Fig.10 Variation curves of critical thrust for different models

图8所示为转速和阻力为0时飞行器的稳定性，可见瞬态坐标系模型产生刚体模态，发生静态失稳，临界推力为0.31Pcr0，与平均轴系模型相比，稳定性降低。

图9所示为转速0 rad/s、α=1.0时飞行器的稳定性，可见考虑阻力时，随着推力增大，瞬态坐标系模型2阶频率不为0，刚体模态频率和1阶模态频率合并，临界推力为0.47Pcr0，与平均轴系模型相比，稳定性升高。

图10所示为不同模型阻力变化对临界推力的影响。由图10可见，随着阻力的增大，瞬态坐标系模型临界推力逐渐增大，当α=0.45时，临界推力基本不变；当α>0.81时，瞬态坐标系模型临界推力大于平均轴系模型。

由图8～图10可知：阻力较小时，瞬态坐标系模型稳定性由刚体模态决定，随着阻力增大，稳定性由刚体模态和1阶弹性模态的耦合模态决定；平均轴系模型稳定性先由1阶和2阶弹性模态耦合模态决定，随着阻力增大，稳定性由1阶模态决定。

3 结论

本文采用Timoshenko梁模型，考虑陀螺效应和剪切效应，运用转子动力学和有限元方法思想，建立推力作用下柔性自旋飞行器横向振动方程，分析了阻力、转速对柔性自旋飞行器稳定性影响。主要得到以下结论：

1)在平均轴系下：①头部集中阻力能够降低系统稳定性，不考虑转速时，使1阶频率趋于0，发生静态失稳，阻力增大，可以使2阶频率趋于0；考虑转速时，自旋能够使1阶反进动频率与刚体模态频率在合并，发生动态失稳，失稳区域变大。②阻力能够使临界推力和临界转速降低，转速使静态失稳变为动态失稳。③转动惯量和剪切效应对稳定性都有影响，与转动惯量相比，剪切效应影响更大，特别是对2阶频率影响。

2)在瞬态坐标系下：推力作用产生刚体模态，系统稳定性主要由刚体模态决定，阻力作用能提高系统稳定性；自旋转速不改变失稳区域。