不同迎角下脊形前体绕流数值模拟研究

陈 浩，袁先旭，毕 林，华如豪，司芳芳，唐志共，傅亚陆，*

(1. 空气动力学国家重点实验室，绵阳 621000；2. 中国空气动力研究与发展中心，绵阳 621000)

0 引 言

新一代高机动飞行器研发过程中，更高的战技性能需求也给空气动力学研究提出了许多新的挑战。例如，国际上的第五代战斗机[1-2]有许多区别于以往战机的重要技术特点，其中最重要的有隐身(Stealth)、超声速巡航(Supersonic Cruise)、超机动飞行性能(Supermaneuverability)和短距起降性能(Short takeoff and landing)，统称为“4S”能力。“4S”性能的实现不仅需要高性能的推力矢量技术，还需要优良的气动布局以及对大迎角状态下前体涡演化的理解和控制。

目前，先进战斗机如F-22和F-35均采用脊形前体，以降低可探测性和实现良好的超声速性能。脊形前体的脊形边缘能吸收雷达波，有效减少雷达散射截面积（RCS），同时，脊形前体高度混合外形也有利于超高速飞行。此外，由于脊形前体的背风流场的涡结构很强[3]，且较稳定，与机翼前缘涡相互干扰，常常能够延迟机翼的完全失速[4]，增加最大升力，并能在有侧滑时提供稳定的滚转力矩，因此提高了飞机的横向稳定性。著名的Su-27飞机的“眼镜蛇”机动就是利用上述原理提升的横向/方向稳定性来扩大其大迎角性能，度过机翼失速[5]。此外，稳定的涡流场也能提高飞机平飞和大迎角飞行时的横向/方向稳定性[6]。

1963年，脊形前体首次用在洛克希德A-12侦察机（Lockheed A-12）上，后续逐步推广应用于YF-12直升机、D-21无人侦察机和SR-71侦察机[7]。尽管国外对脊形前体的静态气动特性已开展了大量研究工作，并应用于工程实际，但由于风洞试验和数值模拟方法等研究手段的局限，对其大迎角状态下流动演化机理和影响的研究尚不充分，而深入了解脊形前体大迎角气动特性，对于工程应用和学科发展而言，均有明确的研究需求。

本文瞄准上述需求，针对脊形前体大迎角湍流大分离流动特点，开展基于DES类RANS/LES湍流数值模拟方法的应用研究，并以此为基础，重点研究了横截面形状、迎角等参数对脊形前体的大迎角气动特性和空间涡流场结构演化的影响规律，为更好地了解其动态特性和进行先进高机动飞行器设计提供参考。

1 数值模拟方法

在脊形前体涡流场以及前体涡与翼型涡干扰的复杂流场中，存在湍流脉动、流动分离等，它们在流场中占据重要位置，直接影响到流场涡结构的形成、演化、破碎与脱落等。

1.1 湍流方程和模型

一般曲线坐标系下，湍流方程可以写作统一的形式：

式中：Φ为湍流变量（如k、ω、v等），F、G、H为对流通量，Fv、Gv、Hv为黏性通量，S p、S D、D分 别为生成项、破坏项和扩散项。

由于本文研究的飞机前体大迎角分离流动的复杂性，综合目前各种湍流方法的优缺点，确保模拟结果能准确地反映气动力非线性特性，本文采用混合RANS/LES方法中的IDDES方法[8-10]，该方法结合了DDES和WMLES方法[8]，可有效解决DES方法中存在的对数层不匹配[8]的问题，同时可节省计算量，并且在包含壁面的复杂流动问题上，能得到比DDES更好的结果。相对于通常的LES和（D）DES，IDDES采用了新的亚格子尺度[10]，其与网格大小和壁面距离皆有关，可实现湍流求解模型的转换。该模型引入混合函数[10]来修正由于RANS和LES交界面相互作用而损耗过多的雷诺应力，提高模型保真度。近年来，很多学者对于该方法进行研究、应用和发展，并取得了大量成果[11-13]。

1.2 数值离散

迎风型NND格式以其形式简单，计算量小，且数值耗散较小，稳定性较好等优势，得到了广泛的应用。本文数值模拟中对无黏项的空间离散都采用迎风型NND格式[14]。

式中，下标i代表网格单元中心位置，i±1/2代表单元界面位置。

对于方程（2），界面无黏通量为：

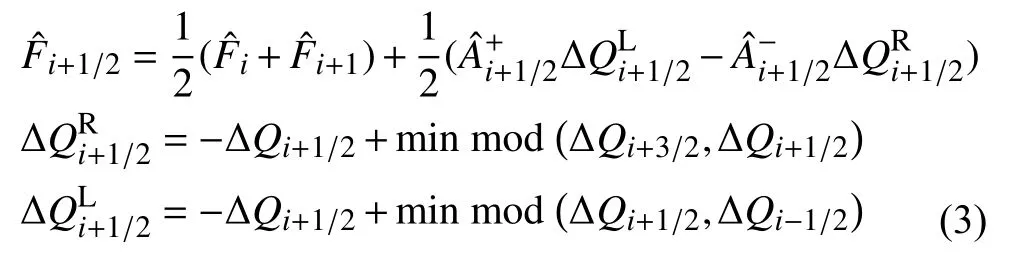
其他方向的无黏通量也是类似的表述。

可以看出，本文采用的空间离散格式为二阶精度。对于具有旋涡、分离等特征的复杂流动问题，采用混合算法或高精度格式可以改善格式耗散特性[15]，并在放宽网格尺度要求的情况下获得高精度的数值解。NND格式本身属于耗散格式相对较小的TVD格式，本文在保证网格量的前提下开展研究，且网格尺度满足该格式对于流动拓扑形态的捕捉[16]。张涵信院士团队曾基于该格式开展了复杂流动问题的模拟，取得了较好的效果[16]。本文将在后续工作中进行高精度格式应用的对比研究。

采用迎风型NND能获得较高的间断分辨率，但也会由于其采用的通量格式而可能带来非物理解。例如，当其通量Jacobi矩阵的特征值很小时，会违反熵条件，产生非物理解，这时需要引入熵修正。本文采用的是Harten熵修正，其表达式为：

一般0.05＜δ＜0.25，在Ma≤ 0.8时，不采用熵修正，即δ= 0；在Ma＞ 0.8时采用熵修正，δ= 0.1。本文计算中Ma= 0.4，未采用熵修正。

为了保证非定常的时间计算精度，同时又具有较高的计算效率，时间推进采用Jameson提出的双时间步[17-19]方法。对于本文发展的DES类混合湍流模型和匹配的非定常算法，课题组成员已经通过典型算例进行了考核和验证[20-21]，确保本文数值方法的有效性和可靠性。

2 计算外形、网格和条件

2.1 计算外形

本文基于某圆形横截面的前体，分别设计了不同脊形角和高宽比的四个脊形前体模型，表1给出了不同外形的参数。选用的脊形前体模型是参考Hall的实验模型数据[22]，最大半宽bmax为38.1 mm，全长为L= 133.35 mm。图1给出了实验模型外形数据和本文根据数据点拟合出来的前体横截面模型的对比。模型宽b、高h与体长x的关系式为：

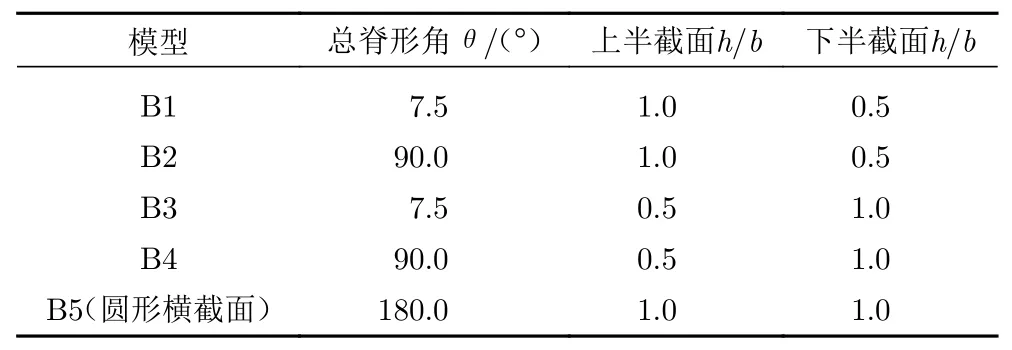
表1 脊形前体计算外形Table 1 Shape parameters of ridged precursors studied

图1 脊形前体计算模型横截面与风洞实验模型数据的比较Fig. 1 Comparison of the cross section between models used in the computation and in the wind tunnel experiment

图2给出了三个前体的整体外形图，因为B3和B4外形分别是B1和B2外形上下翻转得到的，所以不再给出整体外形图以及计算网格示意图。

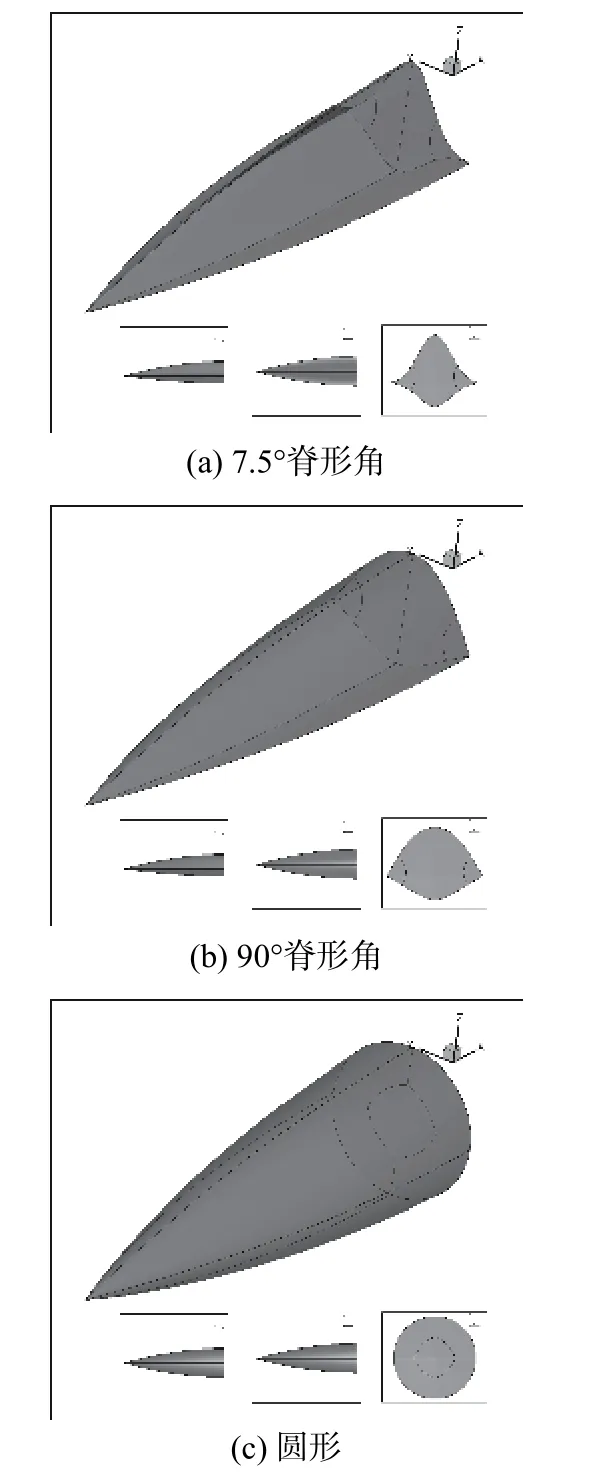
图2 不同前体计算模型Fig. 2 Different models for the forebody

2.2 计算网格

首先考察网格疏密度对计算结果的影响。选取B1前体，分别生成三套不同规模的网格，如表2所示，计算网格均为C-H型，因此仅给出G2计算网格，如图3所示。

表2 不同网格规模Table 2 Different grid sizes

图3 B1模型的计算网格Fig. 3 Computation mesh of the B1 model

取来流马赫数Ma= 0.4，参考面积Sref= 5 086.35 mm2，参考长度Lref= 38.1 mm，单位雷诺数Re/Lref= 9.3×106/m，T∞= 300 K，迎角为30°，湍流模型为SA模型。

从图4中可以看出，三种网格的模拟结果基本一致，因此，在一定网格规模以上，网格大小对气动力系数的影响很小，但稀网格耗时最短，且收敛快。由于IDDES对网格质量要求较高，为了后续计算中能给出较为准确的空间涡结构图，满足IDDES模拟需求，且综合考虑计算效率，以下计算均选用G2网格。其他脊形前体模型的网格生成也参照G2网格的规模。圆形前体的计算网格为O型，网格规模为800万。

图4 气动力系数收敛曲线Fig. 4 Convergence curves for aerodynamic coefficients

2.3 计算条件

本文主要比较静态不同迎角下脊形前体（B1～B5模型）的气动特性和空间旋涡流场。取海拔0 km的大气参数，参考长度Lref= 38.1 mm，单位雷诺数Re/Lref= 9.3×106/m，俯仰力矩中心点Xm= 80.01 mm。取来流马赫数Ma= 0.4，迎角分别为α= 6°、10°、20°、30°、40°、50°、60°、70°，侧滑角为0°。

3 数值结果

3.1 气动力特性

从图5中马赫数为0.4时不同截面前体气动力系数随迎角的变化可以看出，在所考察的迎角范围内，脊形前体的升力系数都明显高于圆形横截面前体B5的升力系数。脊形角为7.5°的B1模型的升力系数极大值出现在40°迎角附近，而脊形角为90°的B2模型和脊形角为180°的B5模型的升力系数极大值出现在50°迎角附近，这表明在脊形角较小时，产生的涡升力较大。α＞ 20°时，随着迎角增加，B1模型CD最大，B5模型CD最小，这表明脊形角越小，相应的阻力系数越大。

B1、B2和B5模型的升阻比对比结果表明，在α＜30°时，脊形角越小，升阻比越大。随着迎角增大，脊形角对模型升阻比影响减小。对比B1、B3和其分别上下翻转后的B2、B4模型可以看出，B1和B3模型K差别很小，B2和B4模型K差别很小，这表明，在考察的迎角范围内，h/b变化对模型的升阻比影响很小。

对比图5（d）中俯仰力矩系数B1、B2和B5可以看出，中到大迎角时，随着脊形角减小，Cm值增大，脊形前体纵向稳定性降低。对比B1、B3和B2、B4可以看出，中小迎角时，上半截面h/b小的脊形前体纵向稳定性较差，随着迎角增加到40° ＜α＜ 60°之间，上半截面h/b较大的脊形前体纵向稳定性较差。

3.2 空间流场结构

图6为不同迎角时用压力着色的Q等值面。图中压力值为无量纲量（当地压强与来流压强的比值）。图7～图9为大迎角时各轴向位置截面物面压力系数周向分布，其采用的是时均处理。图7为各前体在大迎角时在x/L= 1.0截面处截面流线分布。

图5 不同前体气动力系数随迎角变化(Ma = 0.4)Fig. 5 Aerodynamic coefficients variation with the angle of attack for different forebodies (Ma = 0.4)

图6 不同迎角和模型用压力着色的涡量图(Q = 0.003，Ma = 0.4；B1～B5：不同计算模型)Fig. 6 Vorticity iso-surfaces coloured by the pressure at different attack angles(Q = 0.003, Ma = 0.4; B1～B5: Different computation models)

从图6（a）可以看出，具有尖锐脊形前缘（脊形角7.5°）的B1模型，在迎角6°时，自由来流在脊形前缘分离，形成自由剪切层，自由剪切层向上卷起，在前缘附近形成集中的主涡。在迎角10°～30°时，前体主涡Q等值面涡条变得更明显，背风面负压增大，主涡强度增加，其位置向上向内移动，并相继形成了二次涡和三次涡。在迎角40°时，主涡破裂位置移到前体底部以前，升力系数达到最大值。在迎角50°时，主涡破裂位置已前移到距前体头部前半体长以内，轴向位置x/L= 0.7以后背风展向压力第一第二压力极小值已消失，分别表征二次涡和三次涡已破裂。在迎角60°～70°时，主涡在前体头部附近即发生破裂，背风面压力分布基本呈平坦形状，表明背风区流场基本处于完全破裂的大分离状态。

图7 迎角40°时不同截面物面压力系数分布(Ma = 0.4)Fig. 7 Pressure coefficient distributions of different sections at 40° angle of attack (Ma = 0.4)

图8 迎角50°时不同截面物面压力系数分布(Ma = 0.4)Fig. 8 Pressure coefficient distributions of different sections at 50° angle of attack (Ma = 0.4)

图9 迎角60°时不同截面物面压力系数分布(Ma = 0.4)Fig. 9 Pressure coefficient distributions of different sections at 60° angle of attack (Ma = 0.4)

从图7～图9几个轴向位置周向压力分布和图10中轴向x/L= 1.0处截面流线图可见，B1模型的绕流流场保持较好的对称性，仅在迎角大于50°后有轻微的非对称，表明其横侧向气动力很小。

从图6（b）可以看出，对于脊形角为90°的B2模型，在迎角6°时，在较钝脊形前缘的附近形成集中的主涡，与B1模型相似。在迎角10°～20°时，相对于B1主涡，其Q等值面涡条较细，紧贴脊形前缘。在迎角30°时，B2模型的主涡涡条有旋拧现象，破裂不明显，在空间流线可见二次涡和三次涡的位置。在迎角40°时，B2模型的主涡开始在前体底部附近发生破裂。在迎角50°时，B2模型的主涡破裂位置已前移到距前体头部，二次涡和三次涡出现破裂，其升力系数在此迎角达到最大值，相比B1模型要高。在迎角60°～70°时，B2模型的主涡在前体头部附近发生破裂。背风面压力分布基本呈平坦趋势，表明背风区流场基本处于完全破裂的大分离状态，其量值与B1模型的大致相当。

从图7～图9周向压力分布和图11轴向x/L= 1.0处截面流线图可见，B2模型的绕流流场在迎角小于50°前保持较好的对称性，在迎角大于60°后有非对称出现，相比B1模型较明显，进而产生一定横侧向气动力。对比B1模型，相同迎角下，脊形角小时前体主涡强度更大，但较强主涡破裂的临界迎角较小。

图6（c）对应的是B3模型，其与B1具有相同尖锐脊形前缘（脊形角7.5°），但其上下高宽比较大（h/b= 1）。在迎角10°～30°时，B3模型的前体主涡演化与B1模型的类似，三次涡相对不明显。在迎角40°时，B3模型的主涡破裂位置更靠前，二次涡破裂位置更靠后，其升力系数也在此迎角达到最大值。在迎角50°时，B3模型的前体主涡破裂位置和B1模型相近。在迎角60°～70°时，B3模型的前体主涡在前体头部附近即发生破裂。背风面压力分布基本呈平坦形状，其量值与B1模型相比略高。

从图7～图9轴向位置周向压力分布和图12轴向x/L= 1.0处截面流线图可见，B3模型的绕流流场也保持较好的对称性。可以看出，在相同迎角下，上下高宽比较小时，前体主涡强度更大，但较强主涡破裂的临界迎角较小，二次涡破裂延迟。原因是当上高宽比大于下高宽比时，上体对左右涡干扰的隔离作用更强，相对地可以推迟主涡破裂。

图6（d）对应的是圆形截面前体B5模型的流场结构演化。在迎角6°时，可见有前体主涡形成的迹象。在迎角10°时，B5模型的前体主涡最弱，继续向底部延伸。在迎角20°时，模型的底部附近可见较细的集中主涡涡条。在迎角30°时，B5模型的前体主涡涡条变得由头部至底部清晰可见，相对B1模型的较细，未见破裂。迎角40°时，B5模型的前体主涡涡条有旋拧现象，破裂不明显。迎角50°时，B5模型的前体主涡开始在前体前半部发生破裂。迎角60°～70°时，B5模型的前体主涡在前体头部附近即发生破裂。背风面压力分布基本呈平坦形状，其量值与脊形前体模型相比略高。从轴向位置周向压力分布和轴向x/L= 1.0处截面流线图13可见，B5模型的绕流流场也保持较好的对称性。

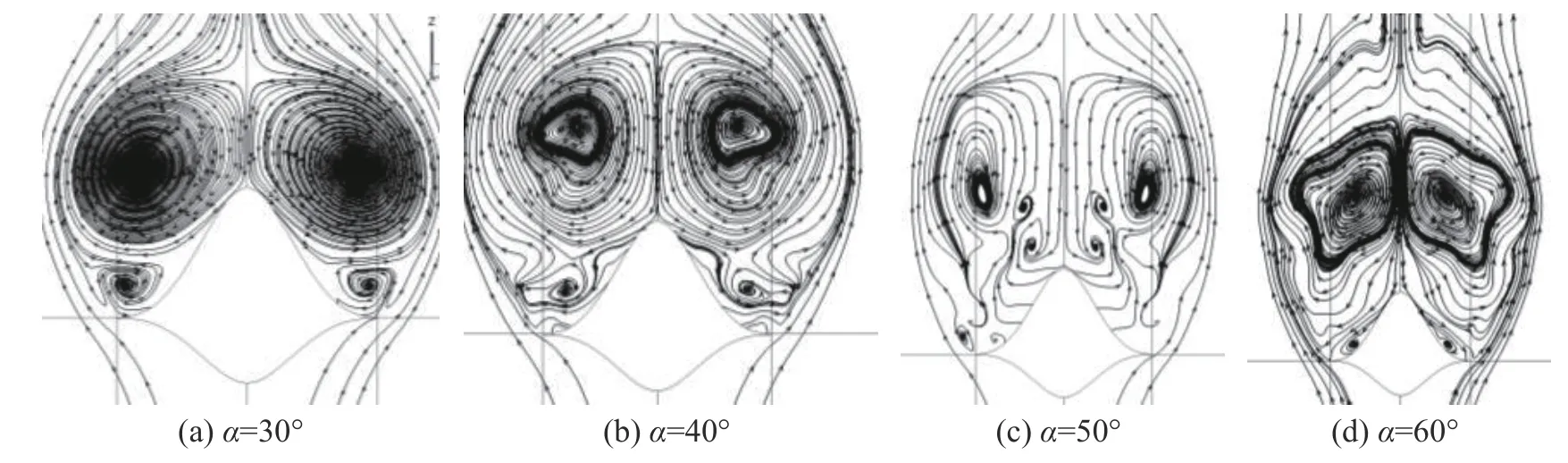
图10 前体x/L = 1.0截面处流线分布(B1, Ma = 0.4)Fig. 10 Streamline distributions at the section x/L = 1.0 (B1，Ma = 0.4)

图11 前体x/L = 1.0截面处流线分布(B2, Ma = 0.4)Fig. 11 Streamline distributions at the section x/L = 1.0 (B2, Ma = 0.4)

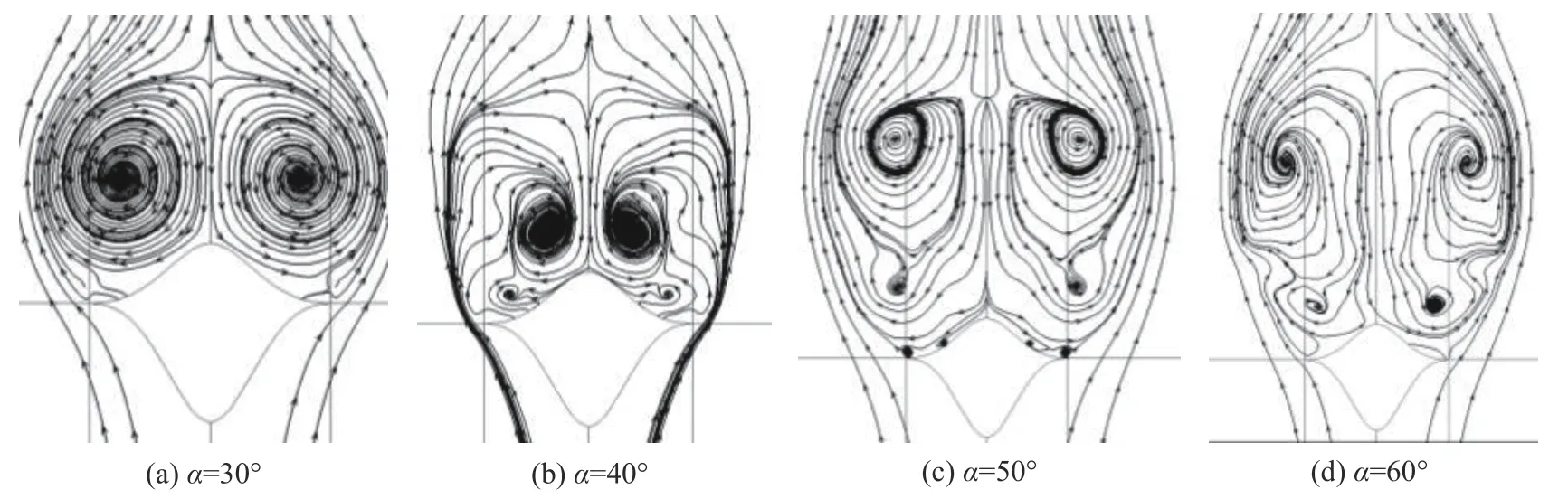
图12 前体x/L=1.0截面处流线分布(B3，Ma = 0.4)Fig. 12 Streamline distributions at the section x/L = 1.0 (B3, Ma = 0.4)

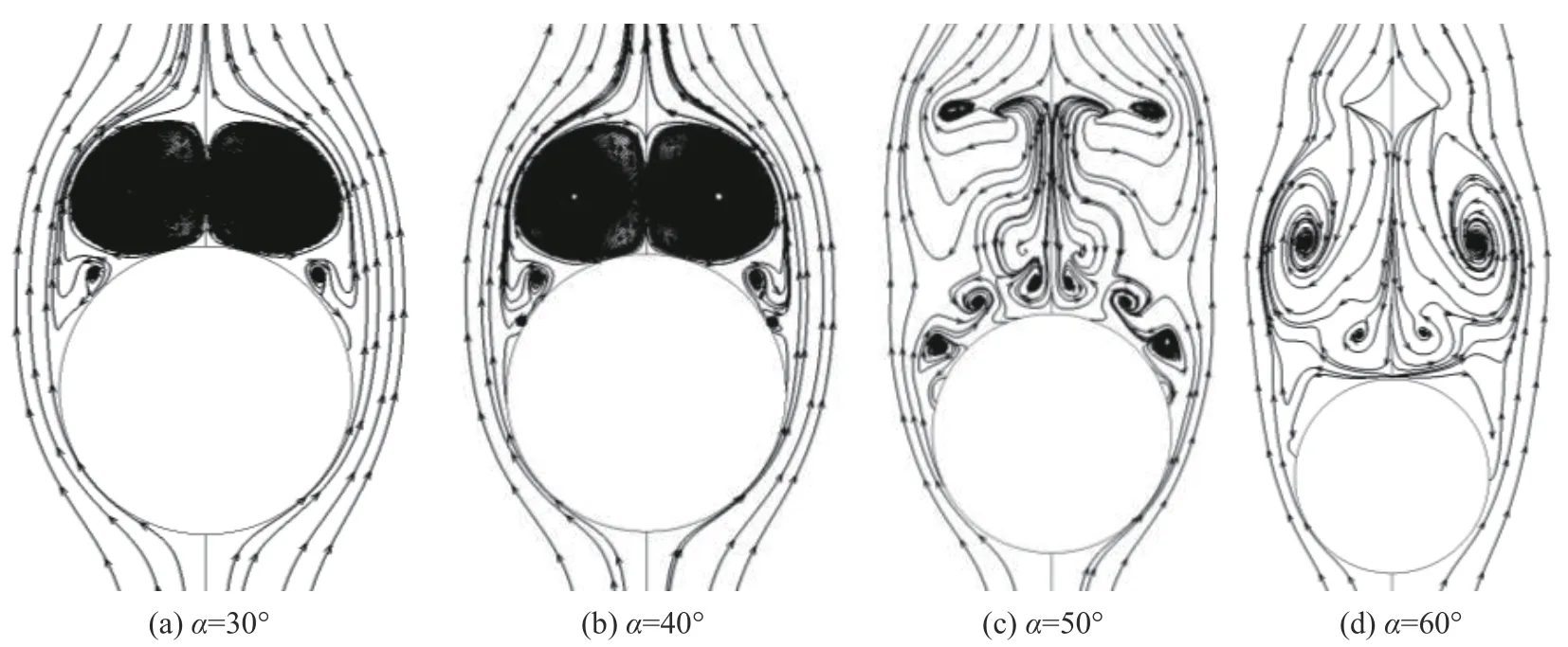
图13 前体x/L=1.0截面处流线分布(B5，Ma = 0.4)Fig. 13 Streamline distributions at the section x/L = 1.0 (B5, Ma = 0.4)

通过上述不同横截面前体在不同来流参数下气动特性的对比，以及气动力特性规律与空间涡结构关联的分析，主要有以下几点结论：

1）迎角变化时，较小脊形角外形的前体主涡强度较大，前体涡产生和破裂的临界迎角较小。在迎角较小时，脊形角越小，较强的前体涡产生的升力越大，升阻比越高；随着迎角进一步增加，不同脊形角的前体涡均破裂，升阻特性趋于一致。在小迎角时，脊形角越小，前体涡升力越大，诱导抬头力矩，因而纵向稳定性变差；在大迎角时，前体涡完全破裂，纵向稳定性改善。与圆形横截面前体相比，脊形前体主涡尽管破裂提前，但相继产生较强的二次涡和三次涡，使得主涡破裂后升力减小平缓，失速特性明显优于圆形截面前体。

2）迎角变化时，对于相同脊形角的前体，上半截面高宽比（h/b）越小，前体主涡强度越大，前体涡破裂临界迎角减小。在迎角较小时，上半截面高宽比小的脊形前体的前体涡虽较强，但二次涡较弱，因而涡升力仅略大，而迎风阻力面积也增大，阻力略增，故升阻比相当。随着迎角进一步增加，上半截面高宽比小的脊形前体，由于左右涡的相互干扰更强，主涡提前破裂，但二次涡破裂延迟，因而升力系数减小，但涡诱导阻力也相应减小，故升阻比仍然相当。此外，迎角较小时，上半截面h/b小的脊形前体，由于涡升力更大，诱导的抬头力矩也更大，因而纵向稳定性变差。随着迎角增加，上半截面h/b小的脊形前体涡提前破裂，涡升力下降，诱导的抬头力矩也减小，故纵向稳定性有所改善。

4 总 结

本文针对脊形前体飞行器大迎角湍流大分离流动计算的困难，采用DES类混合湍流模型，以及与之匹配的非定常算法，开展脊形前体在不同迎角下的静态绕流数值模拟研究，对五种不同横截面形状的前体，数值研究了不同迎角下背风涡流场结构和气动力特性，分析了不同脊形角和上下半截面h/b不同时对前体气动力系数和空间涡结构的影响，主要得到如下结论：

1）随着迎角的增大，前体主涡经历了从形成到增强再到破裂的演化过程，气动升力系数也随之先升高后减小。涡破裂位置和最大升力系数对应的迎角与脊形前体形状有关。

2）脊形角越小，前体涡越强，涡升力越大，产生前体主涡、二次涡、三次涡的临界迎角就越小，前体涡产生和破裂的临界迎角越小。

3）脊形前体不同横截面形状对涡演化的影响规律表现为：相同脊形角的前体，上下高宽比越小，前体主涡强度越大，前体涡破裂临界迎角越小。

4）与圆形横截面前体相比，脊形前体有着较平缓的升力减小趋势，即具备更好的失速特性。并且，脊形前体涡形态较为稳定，对阵风扰动的抵抗能力强，相应地，横航向气动特性会更优良。