非结构嵌套网格中的一种改进型径向基函数插值方法
2019-11-05靳晨晖王刚陈鑫周豪
靳晨晖,王刚,陈鑫,周豪
(西北工业大学 航空学院,西安 710072)
0 引 言
嵌套网格技术在航空航天领域有着广泛的应用,针对一些复杂的几何构型,使用嵌套网格技术可以分区生成网格,减少网格生成的难度。对于飞机副油箱分离[1],座舱盖分离/座椅弹射[2],多级火箭助推器分离[3]等多体分离问题,不同物面间的相对位置会发生变化,同时伴有强烈的非定常效应。常规研究方法如风洞和飞行实验常带有一定的局限性,使用嵌套网格技术进行非定常计算可以对这些过程进行精确数值模拟。
在嵌套网格算法中,一般通过插值实现嵌套区域的流场信息传递,尤其是在解决带有动边界的问题,嵌套区域的网格在每个非定常步内都需要更新,插值模板也需要重新选取。因此,使用正确的插值方法是保证计算结果准确的关键。按照插值方法的不同可分为守恒型插值与非守恒型插值。对于守恒型插值而言,网格尺度对其插值精度的影响较小,但插值过程十分复杂;而非守恒型插值的实现则较为简单,但需要控制嵌套区域网格的匹配程度,否则会损失计算精度。为了减少非守恒型插值过程中的精度损失,一般需要从两方面入手:一方面要改善嵌套插值区域网格匹配程度,如在网格生成时,需要对背景网格中有相对运动的区域进行局部加密,同时使用高效的嵌套装配算法[4]划分嵌套区域,以此来保证物面运动的整个过程中插值单元与贡献单元的匹配程度。另一方面需要研究不同插值方法的插值效果,C.Mastin等[5]研究了双线性、三线性插值方法在嵌套区域的插值效果;田书玲等[6]研究了一种基于Lagrange插值的非结构嵌套网格插值方法;周乃春等[7]使用了逆向距离权方法对嵌套区域进行插值;黄宇等[8]使用了具有二阶精度的插值方法,有效降低了由于在嵌套区域进行插值而引入的误差。仅仅增加嵌套区域的网格量有时也难以达到较好的精度,网格量增加会导致仿真周期成倍增加,占用过多计算资源;同时,线性插值方法在处理复杂问题时的精度相对较低,选择合适的插值方法对于处理不同的问题至关重要。
径向基函数插值方法因其存储十分方便和数据结构相对简单的特点,在近二十年内迅猛发展。研究者们在不同的领域对径向基函数的应用进行大量研究,如R.Franke[9]发现对散乱的数据进行拟合时,使用径向基函数进行插值的精度要高于其他插值方法;林言中等[10]将径向基函数插值方法应用于网格变形技术中的界面数据传递,对AGARD 445.6机翼颤振问题进行非定常计算;刘溢浪等[11]提出一种增量形式的RBF插值方法,并将其应用于有限体积方法的流场重构中;Wang G等[12-13]在RBF网格变形技术的基础上,提出将拉普拉斯光顺与网格变形相结合,有效改善了变形后的网格质量。但是,径向基函数插值半径的选取带有一定的经验性,传统径向基函数前述插值半径选取不合适会严重影响插值的精度与效率。
为了解决嵌套区域的插值精度问题,本文对不同插值函数进行研究,同时采用一种改进的非结构嵌套网格径向基函数(RBF)插值方法。在嵌套网格流场信息传递的过程中,除了使用线性插值(LINE)和以距离倒数作为权重插值(WA)两种传统插值方法,还对逆二次径向基函数(IQ)和Wendland’s C2径向基函数(C2)的插值效果进行研究。针对嵌套边界区域出现的数值奇性现象,通过控制径向基函数的作用半径来调整插值矩阵条件数的方式进行改善。
1 非结构嵌套网格求解技术
1.1 控制方程
为便于对固壁边界的六自由度运动进行描述,采用ALE(Arbitrary Lagrangeian-Eulerian)方法对流动控制方程进行描述。ALE方法允许计算网格的进行刚体运动和变形,通过在流动控制方程中加入网格运动速度,将流体力学中的Lagrange方法和Euler方法进行统一描述。使用ALE方法描述的三维非定常雷诺平均Navier-Stokes方程(URANS)的积分形式为
(1)
式中:Ω为控制体;∂Ω为控制体单元边界;Q为守恒变量,Q=[ρρuρvρwρE]T,其中ρ为流体密度,u、v、w分别为旋转弹在体轴系下三个轴向的运动速度E为总内能;n为控制体单元边界上沿外法线方向的分量;F(Q)和G(Q)分别为N-S方程中的无粘通量项和有粘通量项。
对于式(1),使用格心有限体积法(FVM)进行空间离散后,得到半离散形式为
(2)
(3)
式中:R为计算残差;S为网格单元的面积;n为时间步;Vgrid为网格进行刚体运动的速度。为了保证足够的时间精度,使用二阶向后的欧拉隐式方法[14]求解式(2),如式(4)所示
(4)
式中:Δt为时间步长;上标n为真实时间迭代的步数。直接求解式(4)较为复杂,一般采用伪时间迭代的方法对其进行求解,为此在方程的左端加入一个守恒变量对虚拟时间τ的导数,从而方程的解可以等价为求解一个关于虚拟时间τ的一阶常微分方程组在虚拟时间τ趋近无穷时的渐进解:
(5)
(6)

由于式(5)的精度与伪时间迭代方法无关,因此,伪时间迭代过程可以使用一些加速收敛方法来提高流场的计算效率。具体方法可以参照文献[15-16]。采用改进的LU-SGS[17]算法对式(5)进行向后的欧拉隐式时间迭代,同时使用基于OpenMP并行算法来提高计算的效率。
1.2 嵌套区域划分与贡献单元查找
嵌套网格装配技术的两个核心问题是如何确定嵌套边界和如何查找贡献单元。确定嵌套边界也叫 “挖洞”,当计算网格量较大时,会显著增加预处理的时间,因此高效并且合理地划分出嵌套区域将是嵌套网格装配技术的关键。本文在嵌套区域划分时采取的策略是根据壁面距离来确定嵌套边界区域,同时计算子网格到自身物面和其他物面的最短距离,通过比较到不同物面的最短距离来确定嵌套边界,相比于传统的枚举法,有效减少了前处理时间。节点属性判定如图1所示,i点是属于A网格的网格节点,在求解距离时,距离A网格更近,则i点的属性标记为激活的状态;而j点距离B网格更近,则j点的属性标记为非激活的状态。

图1 节点属性判定示意图Fig.1 Schematic diagram of node attribute determination
当确定了嵌套边界后,需要在嵌套区域查找贡献单元。对于复杂模型来讲,网格量较大,查找贡献单元往往要花费较多时间,因此如何快速的查找到贡献单元是提高嵌套效率的关键。本文根据文献[4]采用了一种基于非结构嵌套网格的“蛇形查找方法”(如图2所示),在空间中以近乎最佳路径的方式查找到了贡献单元,有效缩短了查找贡献单元的时间与距离。假设要寻找i点的贡献单元,该方法的具体实现过程如下:
(1) 在空间中赋予i点一个初始的出发单元,这里假设是1号网格单元;
(2) 连接当前的出发单元的网格格心和i点,判断其穿过当前出发单元的哪一条边(三维为面);
(3) 若穿过某一边(面),则将该边(面)的另一侧单元当做出发单元,循环第二步;
(4) 若没有穿过当前的出发单元所有的边(面),则当前的出发单元就是i点的贡献单元,结束查找。

图2 蛇形查找示意图Fig.2 Schematic diagram of snake search
通过以上步骤,嵌套区域的网格装配完毕。在进行流场计算时,网格实际被划分为三个区域,分别是计算区域、关闭区域和嵌套插值区域。在计算区域,进行正常的CFD求解,当接触到边界时,面外侧位于嵌套区域的网格信息由贡献单元插值得到;在关闭区域,只计算网格单元体积和网格单元面积等预处理操作;在嵌套插值区域,在每个伪时间迭代结束后进行插值,嵌套插值区域的网格不进行计算,而是被当作嵌套边界来处理,这类边界具有插值后获得的流场信息。
1.3 插值方法简介
流场信息的插值传递方法较多,本文主要考察了线性插值、距离倒数权重插值两种传统插值方法,以及逆二次径向基函数、Wendland’s C2径向基函数插值方法。由于线性插值结构较为简单,此处不再赘述,下面重点对其余三种插值方法进行简要介绍。
以距离倒数作为权重来进行插值的原理是:对待插值点附近点进行加权平均,其中权重的大小与需要插值的点与相邻点之间的距离密切相关,与距离呈反比,因此也叫做距离反比插值方法。其具体形式为
(7)
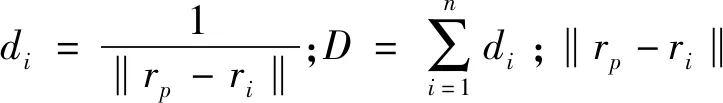
本文所使用的径向基函数的基本形式为
(8)
式中:下标i为支撑点;r为该点的位置矢量;N为网格节点的总数;φ(‖rp-ri‖)为所采用的基函数的形式;ωi为与第i个支撑点相关的权重系数。径向基函数大致可分为以下三类:全局型(Global)径向基函数、局部型(Local)径向基函数、紧支型(Compact)径向基函数,这里简单介绍一下本文所使用的全局型/局部型(IQ)与紧支型(C2)两种径向基函数。
(1) 逆二次径向基函数方法
(9)
在对嵌套区域的P点进行流场信息传递时,根据之前查找得到的贡献单元,将贡献单元以及它的相邻单元一起作为径向基函数的插值模版构建径向基函数的系数矩阵。插值模版示意图如图3所示,i网格是P的贡献单元,则使用i、j、k、l四个网格构建径向基函数系数矩阵。

图3 插值模版示意图Fig.3 Interpolation template schematic diagram
为了选取比较光滑的模版值,在选取模版时,每个物理量减去他们的平均值,最后再加上被减去的值。将各个点的流场信息做差后的ΔZ带入到RBF插值函数之中,得到的线性方程组如下:
ΦW=ΔZ
(10)
(11)
W=[ωi,ωj,ωk,ωl]T
(12)
式中:‖ri-rj‖为欧式距离,即每个基网格格心之间的距离,求解方程后得到每个基网格的权重系数ωi,将需要插值的节点P坐标rP带入到径向基函数中就可以重构出该点的值。
(2) Wendland’s C2型径向基函数
基本形式如下所示:
(13)

插值半径的选取对于径向基函数插值方法的效率有着很重大的影响。较大的插值半径会扩大物面插值的影响域,与此同时,也会使得基矩阵的维度增加并引起计算量的增加。选择较小的插值半径可以减小矩阵维度,降低计算量。
1.4 改进的径向基函数插值策略
径向基函数插值精度高,灵活性很强,使用不同类型的插值函数的插值效果也有所差异。对于同一个径向基函数,选取不同的参数d也会得到不同的插值效果。本文所使用的C2径向基函数,作用半径d的初始值为插值模版中格心和P点(嵌套区域需要进行插值的点)的最大距离的50倍。矩阵的条件数不仅是判断矩阵病态与否的一种度量,也可以表示矩阵计算对误差的敏感度强弱,条件数越大,数值稳定性越差。对于C2径向基函数的系数矩阵Φ,取二范数后的条件数可以表示为:
(14)
为了改善在一些网格上的条件数过大的情况,本文采用了一种基于控制条件数的径向基函数插值算法,通过人为的改变C2径向基函数的作用半径d来调整插值矩阵的条件数,从而在条件数过大的插值模版上进行有效的控制,有效改善了由于条件数过大使得稳定性较差以及出现数值奇性的现象。具体实施的步骤为:当流场求解开始时,人为输入一个期望达到的条件数,当使用径向基函数插值进行流场信息传递时,每次迭代对贡献单元插值矩阵的插值半径自动乘以0.9,计算所有贡献单元插值矩阵的条件数,不满足要求则返回上一步继续缩小插值矩阵半径,直到所有贡献单元插值矩阵的条件数都满足要求。
2 计算结果与分析
2.1 插值精度分析
为了分析本文所使用的插值函数进行解析的精度,使用解析函数作为插值精度验证算例。该函数的数学形式为:
(15)
嵌套网格组装过程示意图如图4所示,圆心在(0,0)处,半径为1。

(a) 嵌套组装前网格

(b) 嵌套完成后网格图4 嵌套网格组装过程示意图Fig.4 Diagram of overset grid assembly process

使用线性插值,以距离倒数作为权重插值,逆二次径向基函数插值、Wendland’s C2径向基函数插值四种不同的方法进行插值,四种插值方法的误差统计如表1所示。

表1 四种插值方式在嵌套区域的误差统计Table 1 Error statistics of four interpolation modes in nest area
从表1可以看出:使用C2径向基函数进行插值具有较小的误差,得到的结果和解析解最为接近。在整个插值的区域内,C2径向基函数插值的平均绝对误差仅为0.007 254 9%,而IQ径向基函数插值为0.036 369%,距离反比函数插值(WA)为0.197 52%,线性插值(LINE)为2.361 2%,说明使用C2径向基函数进行插值具有更高的计算精度,本文将优先选择使用C2径向基函数插值进行流场信息传递。
2.2 MD30P/30N多段翼流场数值模拟
当直接使用C2径向基函数用于嵌套网格插值过程中时,在某些点可能存在数值原因引起的振荡或插值误差过大的点。以MD30P/30N多段翼为例,计算马赫数Ma=0.2,雷诺数Re=9.0×106,迎角α=8.010 9°,湍流模型选择Spalart-Allmaras(SA)。围绕前缘缝翼、主翼、后缘襟翼分别生成计算网格,其中前缘缝翼网格量约为6万,后缘襟翼网格量约为11万,主翼网格量约为22万。三套网格按照之前距离判定的准则自动进行网格嵌套组装。三套网格均按照预期完成组装示意图如图5所示。

图5 MD30P/30N嵌套网格组装示意图Fig.5 Assembly schematic of MD30P/30N overset grid
未采用控制条件数与采用控制条件数后的C2径向基函数插值得到的流场图如图6所示。从流场计算结果来看,直接使用C2函数进行插值得到了图6(a)所示的结果,可以看出:在嵌套区域存在有数值奇性。根据之前提出的条件数控制策略,对于不同的插值模板,通过调整他们的插值半径来控制条件数。经过条件数控制为10,即cond=10时,得到了图6(b)所示的计算结果,整个流场的求解更加光滑,消除了之前出现的数值奇性现象。

(a) 未采用控制条件数

(b) 采用控制条件数图6 MD30P/30N流场计算压力分布云图Fig.6 Pressure distribution cloud diagram of MD30P/30N flow field
MD30P/30N表面Cp分布与实验对比示意图如图7所示,可以看出,当直接使用C2径向基函数插值进行流场信息传递时,表面Cp分布在主翼上表面与后缘襟翼下表面与实验数据差别较大,当采取条件数控制策略的C2径向基函数插值策略将矩阵条件数控制在10后,所得到的翼型表面Cp分布与实验数据吻合度较高,说明该插值方法能够很好地解决直接使用C2径向基函数插值带来的数值奇性问题,且计算精度较高。MD30P/30N残差收敛历程对比示意图如图8所示,当条件数控制在10时,残差下降的速率较快,说明采取条件数控制策略的C2径向基函数插值策略能有效改善残差的收敛效果。

图7 MD30P/30N表面Cp分布示意图Fig.7 Schematic diagram of MD30P/30N surface Cp distribution

图8 MD30P/30N残差收敛历程对比示意图Fig.8 Comparison diagram of MD30P/30N residual convergence process
2.3 AEDC外挂物投放标模验证
AEDC标准外挂物分离模型的计算参数[18-19]如图9所示。计算马赫数Ma=0.95,雷诺数Re=7.874×106,迎角α=0°,湍流模型选择Spalart-Allmaras(SA)。围绕机翼和外挂物分别生成计算网格,网格总数约450万,两套网格按照之前的距离判定的准则自动进行网格嵌套组装。

图9 标准外挂物分离模型的计算参数Fig.9 The calculation parameters of standard separation model
为了考察使用控制条件数策略的C2径向基函数的插值效果,将插值矩阵的条件数控制在100,即cond=100时,如图10所示。从流场计算结果来看,可以看出:未采用控制条件数时,在嵌套区域的边界上,出现了数值奇性,这些异常导致在尾迹区出现了和周围显著不同的区域;当采用控制条件数后,尾迹区流场过渡的更加光滑和连续,这说明采用条件数控制策略的插值方法可以有效消除嵌套边界区域出现的数值奇性的问题。
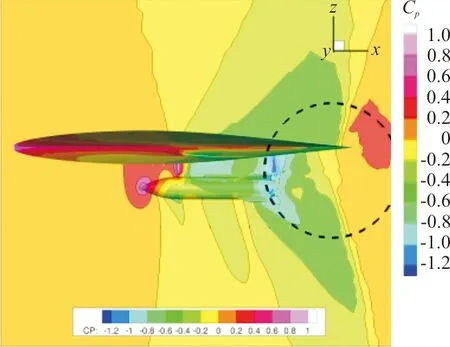
(a) 无条件数控制的z-x截面

(b) 采用条件数控制的z-x截面

(c) 无条件数控制的x-y截面

(d) 采用条件数控制的x-y截面图10 外挂物截面流场对比示意图Fig.10 Flow field comparison diagram of the cross section
外挂物表面Cp分布与实验值对比示意图如图11所示,可以看出:直接使用C2径向基函数和未使用控制条件数策略的C2径向基函数进行插值得到的外挂物周向Cp分布均与实验值较为吻合,当加入控制插值矩阵条件数后,外挂物在弹尾处的Cp分布与实验值吻合度更高一些。

(a) 外挂物两侧表面Cp分布

(b) 外挂物上下表面Cp分布图11 外挂物表面Cp分布与实验对比示意图Fig.11 Schematic diagram of Cp distribution on the surface of the plug-in and comparison with the experiment
AEDC外挂物残差收敛历程对比曲线如图12所示,可以看出:未采用控制条件数时,残差收敛的历程波动较为剧烈;采用控制插值矩阵条件数后,残差收敛效果较好,呈现不断下降的趋势,说明采用条件数控制策略的C2径向基函数插值策略能提高残差收敛的效果。

图12 残差收敛历程对比Fig.12 Comparison of residual convergence process
非定常数值模拟得到的外挂物质心处的位移Xg、Yg、Zg与实验值的对比结果如图13所示,可以看出:采用控制条件数策略的C2径向基函数插方法数值模拟得到的水平位移Xg整体与实验吻合度更高一些。两种不同的插值方式得到外挂物沿竖直方向的位移与实验结果吻合较好。
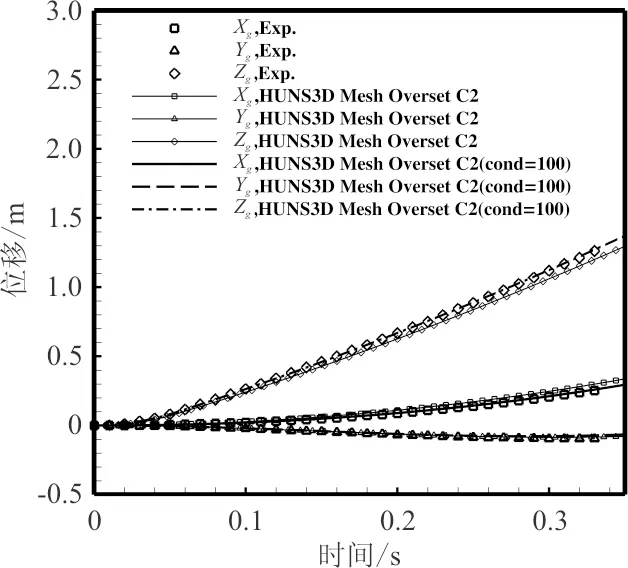
图13 质心位移与实验值的对比图Fig.13 Comparison diagram of center of mass displacement and experimental value
外挂物分离过程中的姿态角变化曲线如图14所示。

图14 姿态角与实验值的对比图Fig.14 Comparison diagram of attitude angle and experimental value
从图14可以看出:使用控制条件数策略的C2径向基函数进行插值得到的俯仰角θ变化曲线在分离中后期与实验吻合更好一些,而偏航角ψ与滚转角φ使用两种插值方法数值模拟得到的结果较为接近,均与实验结果吻合度较高。同时可以看出弹射力矩与气动力的共同作用,使得外挂物的俯仰角θ会呈现先增加后减小的趋势;外挂物受到三角翼下洗与侧洗的影响,偏航角也会逐渐增加。
3 结 论
(1) 使用解析函数作为插值模板,对线性插值、距离倒数作为权重插值,逆二次径向基函数插值、Wendland’s C2径向基函数插值四种不同的嵌套网格插值方法的精度进行验证。计算结果表明C2径向基函数的插值精度较高,同时收敛较快。
(2) 改进后的C2径向基函数插值方法能够有效消除嵌套插值区域数值奇性,同时计算收敛的速率更快,鲁棒性较好。
