一种归一化的代理模型精度指标
2019-11-05张碧辉岳良明王军
张碧辉,岳良明,王军
(1.中国航天空气动力技术研究院 彩虹无人机科技有限公司,北京 100074) (2.中国航天空气动力技术研究院 第二研究所,北京 100074)
0 引 言
代理模型(Surrogate Model或Metamodel)是指通过有限数据,逆向定义一个关于一系列设计变量的连续函数[1]。以代理模型代替原数值分析模型或物理试验,具有使计算量大幅减小但又保证准确度的特点,适用于任何“改变输入反复调用计算模型”的领域[2]。
代理模型种类众多,常见的包括:多项式插值(Polynomial Regression)、径向基函数(Radial Basis Functions)、支持向量机(Support Vector Machine)、神经网络(Neural Network)、克里金法(Kriging)等。Wang Liping等[3]和Jin Ruichen等[4]对以上各种代理模型方法进行了较全面的介绍。
作为一种低成本近似技术,代理模型应具有足够的精度,因此如何衡量代理模型精度成为一项必要的研究工作。常见的代理模型精度检验指标名目繁多,不同文献所采用的指标各异。常见指标有:标准残差值SR[5]、误差平方R2[4]、均方根误差RMSE[6-7]、正则化均方根误差NRMSE[8]、相对最大绝对误差RMAE[6-9]、相对平均绝对误差RAAE[6]、代理模型接受率MAS[9]、平均百分比误差APE[10]等。
总结以上各种指标,计算过程中普遍采用:
(1) 函数真值与模型预测值之差的绝对值;
(2) 先求出函数真值与模型预测值的差值,再计算该差值与函数真值的比值;
(3) 先求出函数真值与模型预测值的差值,再计算该差值与函数真值标准差的比值。
在代理模型的应用中,通常在选定一种模型后,对多种数据分别进行拟合。例如,飞行器气动参数的研究,需要对升阻力系数、俯仰力矩系数等一系列气动参数进行建模,但是对于具有不同单位制、不同数值的两种数据,以上代理模型精度指标无法将二者进行横向比较:
(1) 飞行器的阻力系数数值都小于1,而力矩系数数值可能达到上百,第一类方法显然不可取;
(2) 某些气动参数数值分布在0的附近,会导致第二类方法得到的指标值失真;
(3) 采用第三种方法,模型精度会受到函数真值分布情况的影响。一般情况下,样本点越分散越能够包含更多函数信息,则模型越准确。但是认为模型准确度与样本点的标准差成反比是不合理的。
为了解决以上问题,实现对代理模型不同种类拟合数据的横向对比,本文提出归一化绝对误差均值(Mean Normalized Absolute Error,简称MNAE)来表征模型准确度,并通过某飞行器算例的计算结果,以证明该指标的有效性。
1 归一化绝对误差均值
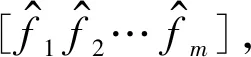
(1)
根据代理模型预测数据的性质,当真实函数值同时为正或同时为负时,取:
(2)
当真实函数值既有正数又有负数时(即跨越0时),取:
(3)
于是,任意函数真实值的归一化为
(4)
任意函数模型预测值的归一化为
(5)
代理模型的准确度,定义为归一化后真实值与归一化预测值差值的绝对值的均值:
(6)
MNAE值越小,说明代理模型预测精度越高。MNAE值的定义,重点在于归一化计算的上下界如何确定。对于样本函数值“同时在零点一侧”和“分布区间跨越零点”两种情况,分别选择不同的方法计算上下界。本文将上下界的区间设定的足够大,以使得所有样本点函数值归一化之后都落在(0,1)区间。
2 算 例
本节算例为某型战术导弹。导弹弹体为圆柱形,弹头为圆锥型,弹翼采用常规式纵向布局、“X”型周向布局,主翼、尾翼均采用双弧型对称翼型,尾翼为全动舵面。其主要尺寸如图1所示。
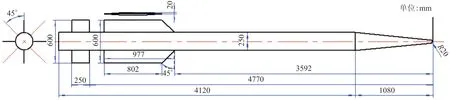
图1 导弹主要几何尺寸示意图Fig.1 Dimensions of the missile example
导弹的外形设计参数确定后,调用Missile Datcom[11]计算不同飞行状态下的气动数据,得到代理模型样本点。
表征不同飞行状态的代理模型设计变量包括:攻角、侧滑角、速度、高度、飞行器重心位置,其取值范围如表1所示。

表1 设计变量及取值范围Table 1 Design variables and range
根据飞行器仿真程序的需求,气动数据共有11种,如表2所示。
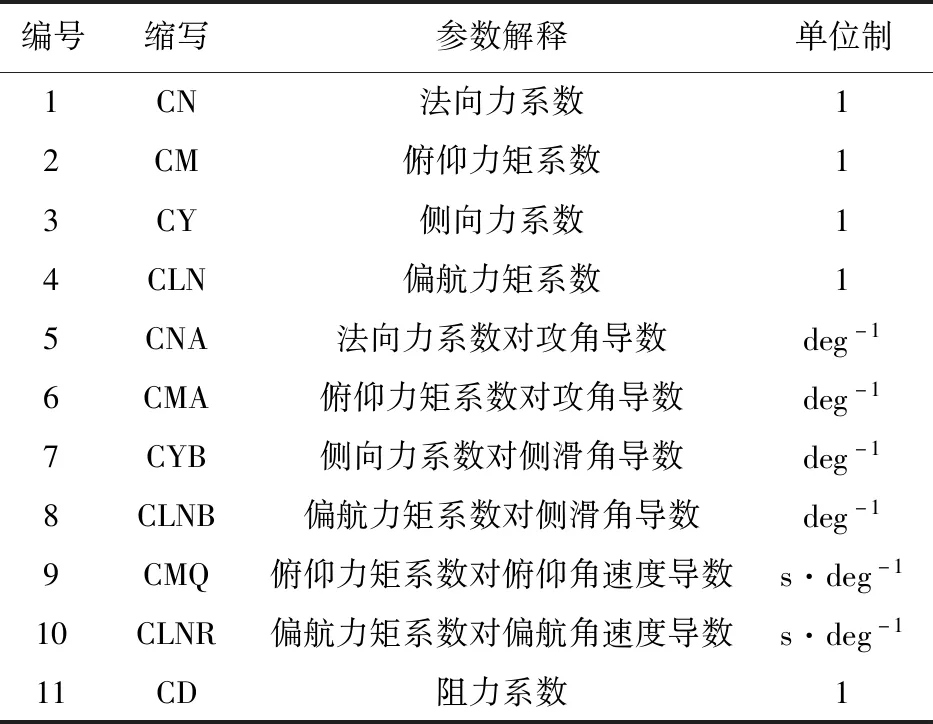
表2 气动数据明细Table 2 Explanations of aerodynamic coefficients
3 Kriging模型及相关方法
Kriging模型的思想[12]是由南非工程师D.G.Krige于1951年提出的,之后发展成为一种地质统计学插值方法。1989年,J.Sacks等[13]将Kriging理论进一步推广到确定性计算机实验领域,并给出了一种较实用的Kriging算法。此后该方法在众多研究领域得到发展和应用。Kriging模型的基本思路详见文献[14]。Kriging模型在各种代理模型方法中建模工作相对复杂,但其拟合能力较强,在飞行器气动参数拟合领域得到广泛应用[15-17]。
实验设计是建立代理模型的必要准备工作,它的主要内容是:在设计变量空间内合理地布置有限的样本点,使其能够获得尽可能多的函数信息。常见的实验设计方法包括:拉丁超立方(Latin Hypercube)、正交表(Orthogonal Array)、蒙特卡洛法(Monte Carlo)等[18]。
对于飞行器气动性能这类复杂问题,响应函数在设计空间上的分布特性通常难以把握。本文在初次建立代理模型时选择较少样本数量,建立气动函数的粗略分布规律;基于初始样本得到的代理模型,通过一系列加点方法加入新的样本点,进而迭代修正代理模型。
根据文献[19],本文Kriging模型建模过程中每次添加:函数极小值点,与现有样本距离之和最大点,预测方差最大点,改进期望值取不同系数所得到的5个最大值点。共计8个样本点。
以上各极值求解均选用遗传算法进行优化求解。
根据文献[20],气动数据代理模型中总存在着一些“奇异点”,它们的真实值与代理模型预测值之间的误差很大,且不会随着样本点的增加而有所改善。剔除与“主流”数据点响应趋势不相符的“奇异点”能显著改善模型精度。本文在每一轮加点的同时,同样采用遗传算法求解出模型检验指标最差的3个点,将其从样本点中剔除。
综上,先增加8个样本点再删除3个样本点,一次样本更新后样本点数增加5个。
除了确定模型精度指标之外,计算模型精度的策略主要分两种:加点验证方法和交叉验证方法。加点验证方法简单直观,但却不能充分利用全部样本点来构建代理模型。交叉验证方法的基本思想可以简单描述如下:首先将样本点集S随机分成样本数目大致相等的m个样本点子集,在验证代理模型精度时,将其中的任一个样本点子集作为待验证的数据,其余的m-1个用于构建接受检验的代理模型,这样可以得到该子集对应的验证误差;当遍历m次,所有样本点子集都充当了验证数据后,就可以得到所有子集的精度指标。本文采用交叉验证方法进行代理模型精度检验。
综上所述,本文Kriging代理模型的建模、加点、检验方法流程如图2所示。

图2 代理模型建模流程Fig.2 Modelling process of the surrogate
4 计算结果
为了验证代理模型精度指标的准确性,将MNAE值与相关性图进行比较。
相关性图以最直观的方式表达代理模型的准确度:它的横坐标为一组输入数据的真实函数值,纵坐标为相同数据经过代理模型得到的预测值。相关性图中数据点的分布越接近y=x这条直线,说明代理模型预测得越准确。相关性图的局限性在于其分布情况只能通过目视观察,而不能给出定量的指标。
根据第3节所述方法,得到各气动参数70样本点Kriging模型的相关性图,如图3~图13所示。根据使用经验,阻力系数CD的Kriging模型选择二阶回归项与Gauss相关函数,其他气动参数统一选择一阶回归项与Exp相关函数。考虑个别气动系数集中分布在距离零点较远处,为了准确表达Kriging模型预测精度,各参数相关性图均包含零点。
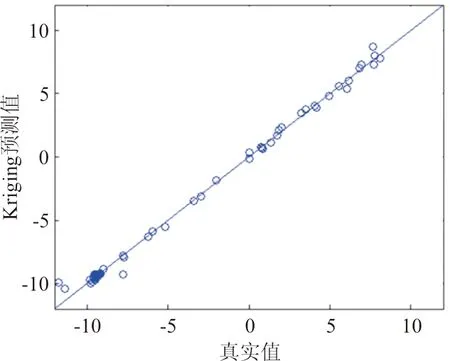
图3 CN系数相关性图Fig.3 Regression plot of CN

图4 CM系数相关性图Fig.4 Regression plot of CM

图5 CY系数相关性图Fig.5 Regression plot of CY

图6 CLN系数相关性图Fig.6 Regression plot of CLN
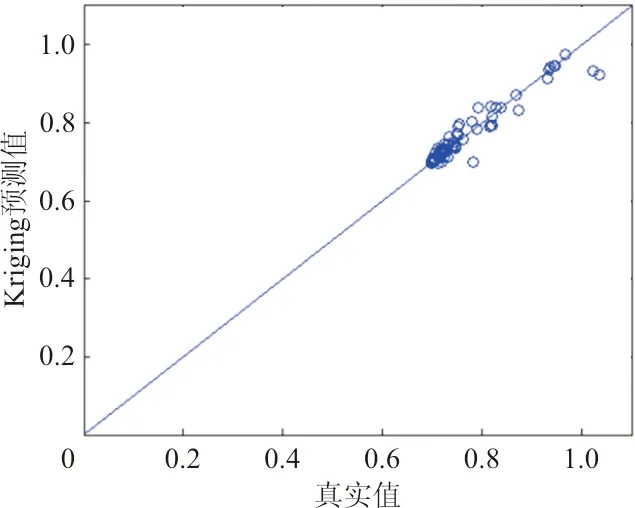
图7 CNA系数相关性图Fig.7 Regression plot of CNA
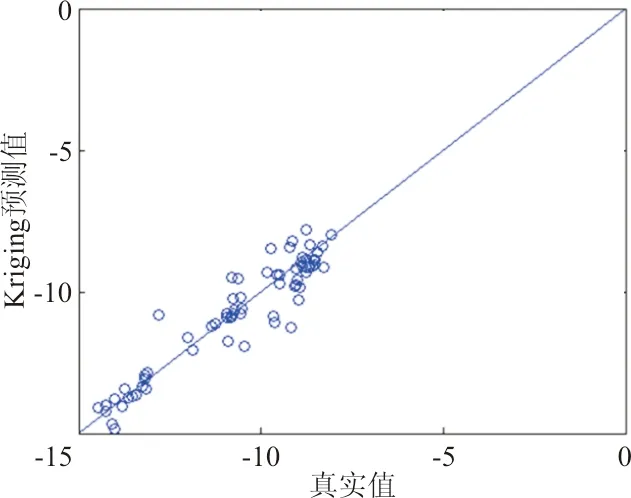
图8 CMA系数相关性图Fig.8 Regression plot of CMA
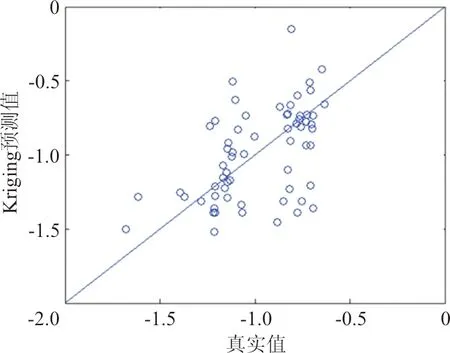
图9 CYB系数相关性图Fig.9 Regression plot of CYB
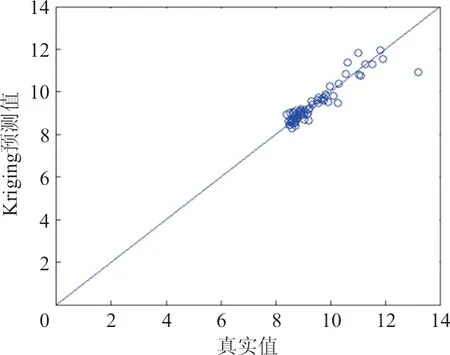
图10 CLNB系数相关性图Fig.10 Regression plot of CLNB
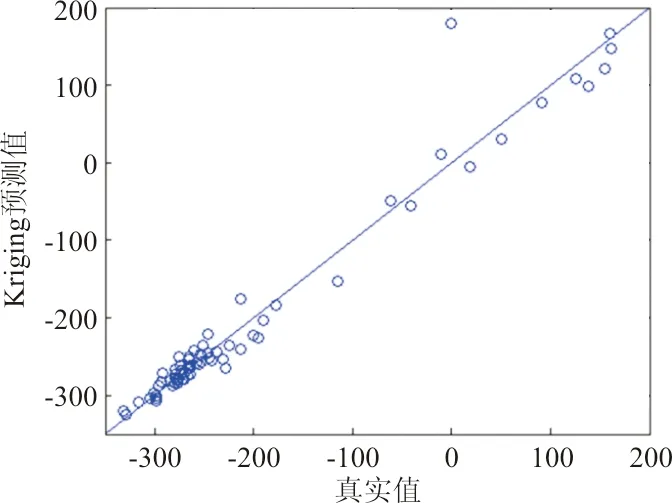
图11 CMQ系数相关性图Fig.11 Regression plot of CMQ
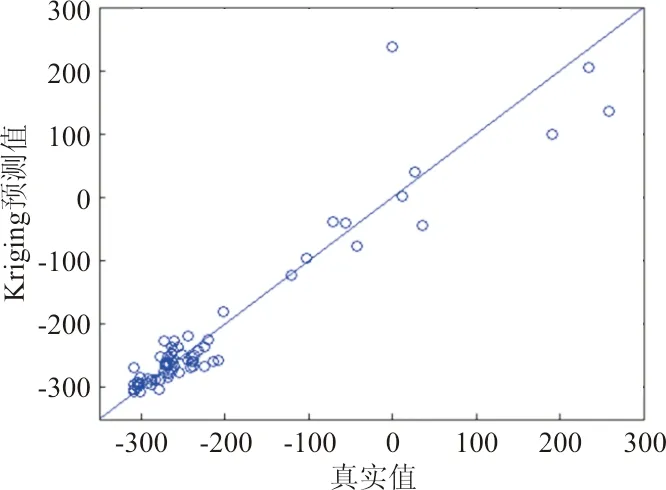
图12 CLNR系数相关性图Fig.12 Regression plot of CLNR

图13 CD系数相关性图Fig.13 Regression plot of CD
不同气动系数分布规律不同,拟合难度不同,所得到的Kriging预测准确度自然也不同。对比图3~图13,按图中数据点与直线y=x接近程度将各系数分类,结果如下:
预测准确的系数:CY、CD、CM、CN、CLN、CNA
预测较准确的系数:CLNB、CMA、CMQ、CLNR
预测不准确的系数:CYB
将各系数的MNAE值按照从小到大排列,结果如表3所示。
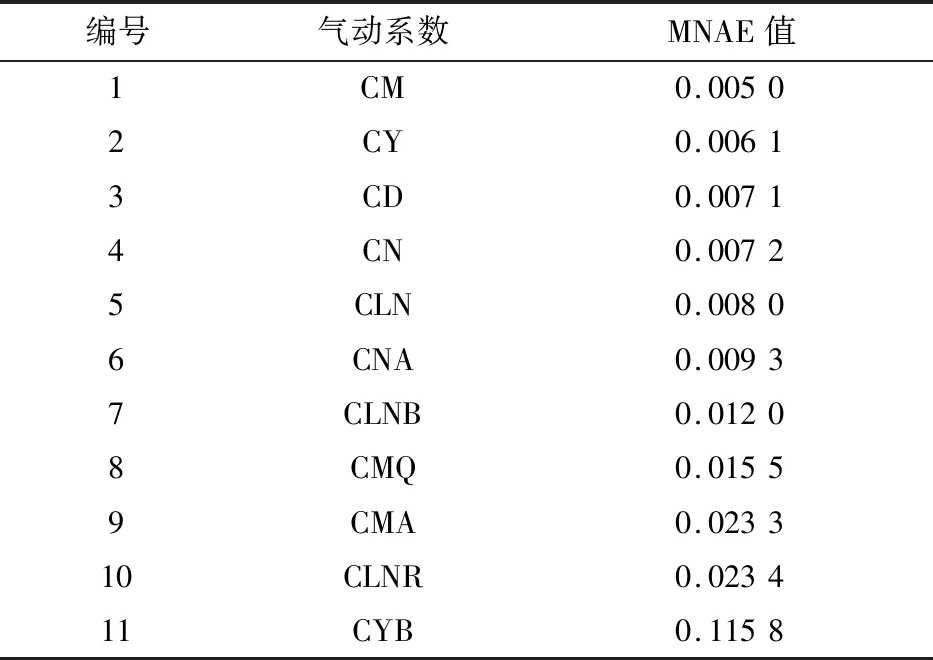
表3 各系数MNAE值列表Table 3 MNAE value of aerodynamic coefficients
由相关性图得到各系数预测准确等级,将其与MNAE值进行比较,可以发现二者一致。表明在横向比较不同类型数据时,MNAE值能够较好地表征代理模型的准确度。
5 结 论
基于算例对11种气动参数的计算结果,通过对MNAE值与相关性图的比较,验证了本文提出的精度指标不仅能够有效表征代理模型的准确度,而且可以对不同类型的数据进行横向对比。
