CFD技术在目标电磁特性计算中的应用

2019-11-05许勇黄勇孙俊峰

航空工程进展 2019年5期

许勇，黄勇，孙俊峰

(中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000)

0 引言

复杂外形目标的电磁散射具有复杂散射机理，通常包括镜面散射、边缘绕射、爬行波、表面波、几何非连续结构散射等复杂电磁现象，准确模拟非常复杂和困难。另一方面，发展快速高效、精度高的军用复杂外形飞行器的电磁散射计算方法为气动/隐身优化设计所迫切需要。传统的高频渐进方法和部件分解法等虽有方法通用、快捷，易于目标建模和能捕获主要散射特征的优点，但也有计算误差较大的缺点。目前国内外发展的电磁散射数值方法主要包括两类：一类是求解电流积分方程，典型的例如多层快多极子(MLFMA)方法[1-4]；另一类是求解微分方程的FDTD方法[5-7]以及有限元(FEM)方法。积分方程方法采用格林函数避免电磁波在空间传播的耗散、色散误差，但会带来稠密的耦合系数矩阵；微分方程方法直接计算电磁场，涉及场的时空计算、传播和累积误差，但也有适用问题广，易于编程的优点。

电磁学麦克斯韦方程组和流体力学无粘流欧拉方程都是有实特征值的双曲型偏微分方程组，相同的数学特性允许采用同样的偏微分数值算法。时域有限体积法(FVTD)[8-11]广泛应用于CFD工程中，该方法采用贴体曲线坐标系，避免了传统FDTD[5]中笛卡尔网格带来的阶梯效应误差，不同于FDTD二阶中心差分格式和利用电磁场量时/空错置来提供人工粘性，FVTD利用迎风格式和一定网格密度来降低数值计算中的耗散和色散误差，其计算机存储与未知量数目同数量级，此时间推进方法能相容地模拟散射、多重散射、孔穿透、腔激励等复杂现象而不需特殊处理。国外，在前期导电体电磁场计算的基础上，FVTD目前主要发展在应用层面，例如集成电路设计，FVTD和高频混合方法计算电大目标电磁散射。D.K.Firsov等[12]研究了FVTD和积分方程(IE)结合节省计算空间和网格量；A.Chatterjee[13]研究了代数多重网格技术和FVTD方法结合来有效模拟线性电磁波传播及保证高阶空间离散精度。国内，前期主要的FVTD研究工作侧重于完全导电体电磁散射计算和多学科优化应用[14-16]。2014年，聂在平等[17]提出：超电大目标、介质/导体混合结构、腔体以及多尺度电磁散射问题面临工程挑战，目前基于CFD的电磁解算器仍有所欠缺。

为此，本文扩展FVTD方法在目标电磁散射问题中的应用，首先，发展宽带信号入射电磁波FVTD方法，在一个非定常过程计算多个频率电磁散射；然后，发展特殊通量计算方法计算介质/金属目标电磁散射问题；最后，发展并行FVTD方法数值计算电大尺寸目标电磁散射问题。

1 数值方法

任何电磁问题的电磁场解都满足如下时变麦克斯韦方程组：

(1)

(2)

(3)

(4)

式中：B为磁感应强度矢量；H为磁场强度；D为电位移矢量；E为电场强度矢量；J为自由电流密度；ρ为自由电荷密度。

无源情况下，例如在自由空间中，J=0，ρ=0。

时变麦克斯韦方程组在直角坐标系下的守恒形式为

(5)

其中，

对于复杂外形物体，经坐标变换：

得到曲线坐标系下的麦克斯韦方程组守恒形式为

(6)

其中，

(7)

式中：V为坐标变换的雅可比矩阵行列式值。

有限体积法的特点是能保持整个网格空间的通量守恒，对守恒方程(6)在每个网格单元作时间、空间积分，可以得到方程的数值离散化形式：

(8)

有限体积法的空间精度体现在能否精确模拟原变量Q在网格单元分界面处的状态变量，以得到相应精确的分界面流通量F。流通量的计算采用Steger-Warming分裂，也可通过求分界面处的黎曼(Riemann)解等方法得到。

(9)

式(9)中的单元边界左右流通量可统一写为

(10)

(11)

式中：k=ξ,η,ζ；S,S-为相似矩阵；Λ+,Λ-分别为正负特征值构成的对角矩阵；QL,QR分别为分界面处左右状态变量，可采用MUSCL格式得到最高三阶精度。

(12)

(13)

完全导电壁面反射边界条件，由电磁理论为

(14)

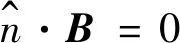
(15)

式中：E,B为总场。

式(14)～式(15)是不完备的，未提供电场垂直表面、磁场切向于表面信息，补充近似边界条件：

(16)

(17)

本文借鉴CFD中固壁边界处理方式，发展了三种可行的完全导电体(PEC)边界条件，分别是1、2阶外插边界条件以及虚拟像点方式，虚拟像点方式有通用性，有利于数据交换和并行通信。

截断网格外边界采用辐射边界条件或吸收边界条件，以降低边界反射回波带来的畸变。本文采用相容条件：

(18)

时间计算方面采用与常微分方程相似的龙格-库塔方法：

Qn+k/m=Qn-λαkR(Qn+(k-1)/m) (k=1,m)

(19)

其中，

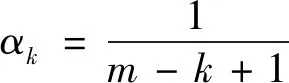
式中：m为龙格-库塔法的步数，本文中m=4；R为方程的残差。

2 电磁散射特性计算

2.1 宽带脉冲电磁波入射

时域方法的一个重要优点是在宽带脉冲电磁波入射情况下，利用非定常计算和傅里叶变换，在一个计算状态中可以获得多个频率目标电磁散射特性。

入射信号采用高斯脉冲：

(20)

频谱强度由对应的非周期信号傅里叶变换计算：

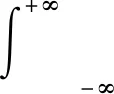
(21)

本文实际计算中从5倍半周期Tm信号，即5×Tm开始，整个网格密度由待求最高频(最短波长)决定，如此低频信号网格密度自然满足精度要求，停止计算条件为积分面上最大电磁场幅度小于-18 dB。

以高斯型宽带脉冲电磁波入射情况下的金属球雷达散射截面计算为例，网格为49×121×61。输入电磁信号如图1所示，频谱分布如图2所示，金属球宽带信号电磁散射中电磁场时间历程和3个频率对应双站RCS分布如图3所示，可以看出：与对应解析解吻合很好。

图1 入射高斯型脉冲电磁波信号Fig.1 Incident electromagnetic wave of Gaussian pulse

图2 频谱分布Fig.2 Spectrum of frequency domain

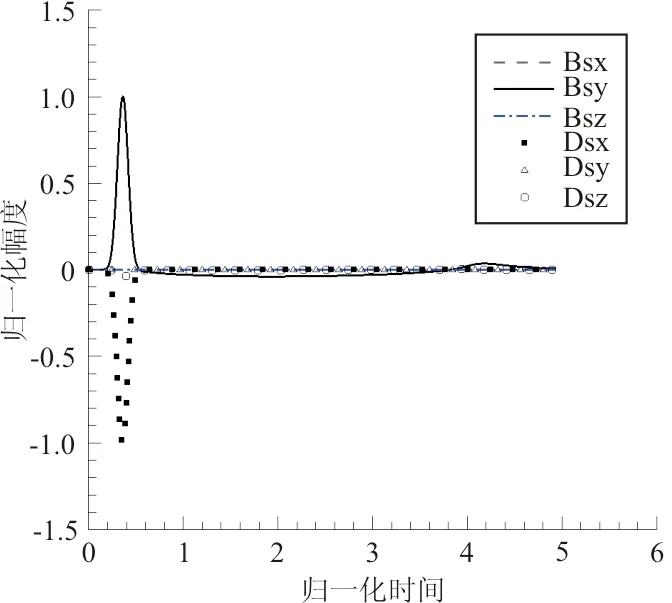
(a) 脉冲散射场时间历程

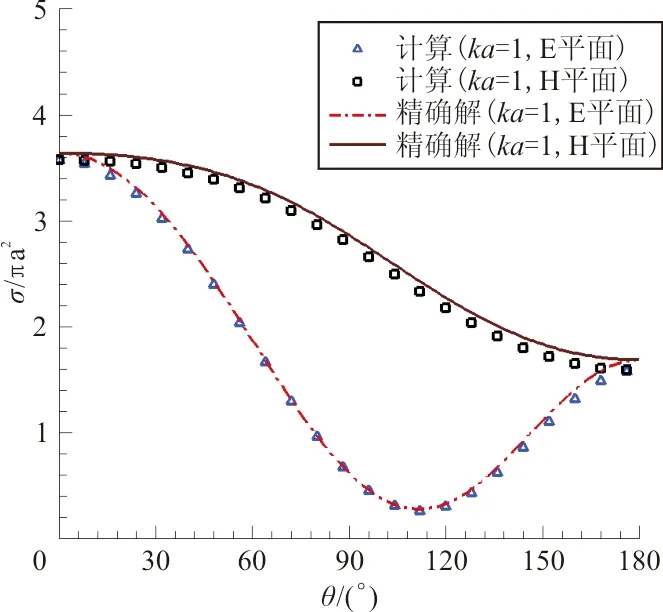
(b) ka=1

(d) ka=10图3 宽带脉冲波入射金属球雷达截面(RCS)计算Fig.3 Bistatic RCS profiles of incident wideband signal with different frequency

2.2 介质/金属目标电磁散射计算

介质通常指不同于自由空间，其普遍形式是具有复数型介电常数和磁化率，实部引起电磁波折射，虚部引发电磁波耗散。采用散射电磁场守恒形式，电导率和磁导率分别为：σe=ωεi，σm=ωμi。利用介质电磁参数间断处电位移矢量、磁感应强度切向分量连续插值和构建通量。

(22)

(23)

一类不同磁化率介质覆盖金属球的双站RCS计算结果如图4所示。计算条件：ka=6.28，介质厚度：d=λd/30 。

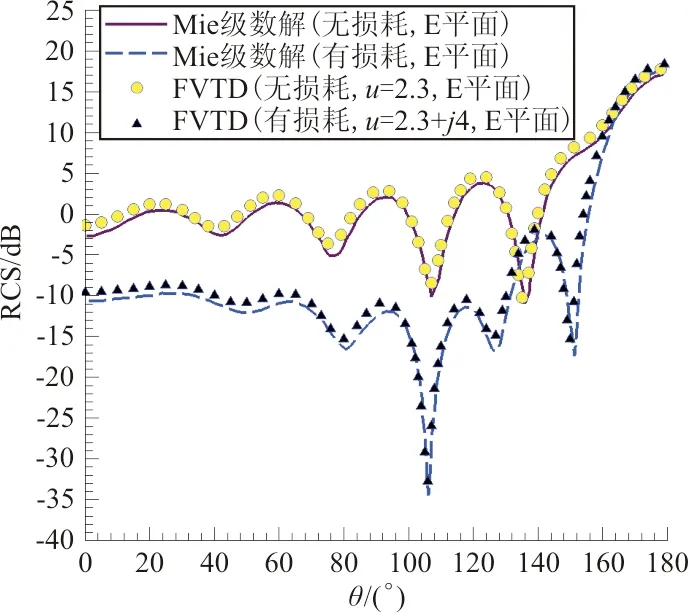
(a) E平面

从图4可以看出：介质虚部引发电磁能量耗散，相应降低散射电磁波能量，从而带来RCS降低，这也是等离子体隐身机理的验证。

2.3 电大尺寸金属目标电磁散射计算

FVTD方法直接求解麦克斯韦方程组，是全波数值方法，适用于从低频到高频全范围，但由于空间网格数量与频率平方成正比，对每个波长如取大于15个网格点情况下，战斗机X波段网格数量达到数十亿规模。对超电大尺寸目标必须辅以并行算法，因涉及电磁波在三维计算空间传播，其完全导电体电磁散射计算效率比不上多层快多极子方法(MLFMA)。

高频电大尺寸目标电磁散射问题中，三维空间网格的大幅增长使得计算量十分庞大，并行计算势在必行，因此构建多进程并行平台，包括：①网格多进程分割和负载平衡，②程序并行化处理，采用MPI接口进行通信。文献[11]详细介绍了该并行解算器的验证和相关细节。本文验证计算算例为美国EMCC标模。归一化表面诱导电流等值线云图如图5所示，显示电磁反射强度区域分布，截断锥台单站RCS计算与测量比较如图6所示。高度200 mm,底部直径200、100 mm,计算频率7 GHz,平行极化，计算验证FVTD模拟边缘绕射和爬行波的能力。使用多块结构网格，包含257万网格点，采用100个进程，由于并行FVTD程序结构同于CFD解算器，其并行效率亦同于CFD中并行有限体积法流场解算器。