一种新型乘波体设计方法研究
2019-11-05陈立立郭正邓小龙侯中喜汪文凯
陈立立,郭正,邓小龙,侯中喜,汪文凯
(国防科技大学 空天科学学院,长沙 410073)
0 引 言
近年来,高超声速飞行器因其杰出性能备受各国重视。吻切锥乘波体是一种非常重要的高超声速飞行器设计构型[1]。传统的吻切锥乘波体在给定上表面出口型线(Flow Capture Curve,简称FCC)和下表面激波出口型线(Inlet Capture Curve,简称ICC)后,其构型就确定了。对于乘波体而言,升阻比和容积率是两个相互制约的因素,如何设计出既具有较高升阻比又能保持较高容积效率的乘波体,一直是重要的研究方向[2]。
目前,高超声速飞行器设计主要基于乘波体概念,设计方法包括:楔导法、锥导法、楔锥法和吻切锥方法等。国内外已对乘波体构型的设计进行了诸多探索,例如,王发民等[3]采用纵向对接乘波体方法设计了宽速域乘波飞行器,兼顾低速和高速性能;李永洲等[4]提出了一种可同时控制前后缘型线的乘波体设计方法,使得后缘出口流场均匀,有利于与进气道进行匹配;许少华等[5]采用正交试验方法对圆锥半顶角、底部基线形状等参数进行分析,研究了锥导乘波体设计参数的敏感性;张翠娥[6]研究了锥导乘波体的设计,并对激波角、半展角、长宽比和膨胀角等参数对升阻比和容积率的影响进行了分析,得出当激波角为11.5°左右时乘波体的升阻比达到最大;C.E.Cockrell Jr等[7]研究了平面翼乘波体和弯曲翼乘波体的气动性能,研究表明乘波体是突破升阻比屏障的重要手段;M.J.Lewis等[8-9]采用吻切锥乘波体设计飞行器前体,使得发动机入口获得更均匀的流场;P.E.Rodi[10]通过吻切锥方法,设定乘波体前缘后掠角度产生新的乘波体布局,利用前缘产生的涡增大背风面的负压,来提高整体的升阻比;季廷炜等[11]建立了乘波构型的设计代理模型,并基于该模型进行了性能分析和优化;K.Cui等[12]提出了高压捕获翼构型,并说明这类飞行器具有较高的升阻比和容积率;S.B.Li等[13]提出了一种变马赫数宽速域乘波体设计方法;A.Ueno等[14]在对基准模型进行风洞试验的基础上,提出了改进高超声速飞行器底部构型而减少阻力的方法,该方法建议乘波体底部截面应该被修改为凹面型以达到减阻的目的;L.L.Chen等[15]基于吻切理论设计了变激波角乘波体,通过改变激波角分布研究了变激波角乘波体容积率和稳定性的变化规律;丁峰[16]首次提出“全乘波”气动设计理论,提出了基于任意超声速轴对称基准流场的通用型乘波体设计方法,并针对新型冯卡门乘波体进行了详细分析。
虽然国内外研究人员已对乘波体构型的设计进行了系统且相对全面的研究,但是乘波体固有的容积率和气动性能之间的矛盾仍然存在,如何设计出既有较高容积率又有较高升阻比的乘波体飞行器依然是研究难点。本文在对圆锥流场进行详细分析的基础上,提出一种释放部分几何约束的乘波体设计方法。该方法通过引入一条新的设计曲线来实现不同乘波体构型参数的调整,以期拓宽乘波体的设计空间,使乘波体的容积率和升阻比可以在一定范围内有效控制。
1 基准流场求解
在高超声速圆锥绕流中,激波前后的流场满足Taylor-Maccoll控制方程[17],采用临界声速无量纲化的表达式(式(1))和四阶龙哥库塔(Runge-Kutta)求解流场。
(1)
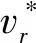
(2)
(3)
则
(4)
(5)
式中:γ为比热比;R为气体常数;T为静温;Tt为总温。
2 新型乘波体设计方法
新型乘波体设计示意图如图1所示,给定出口激波型线(ICC)和上表面出口型线(FCC),建立FCC和ICC的一一对应关系,根据不同切面处的激波半径设计得到相应的激波圆心,这些激波圆心形成一条激波圆心曲线(Curve of Center of Shock,简称COC)(或者提前给定COC曲线,激波半径所在直线与COC曲线的交点就是当地激波圆心),近似认为这些平面就是当地吻切面,然后基于吻切锥设计方法得到一个新型乘波体构型。
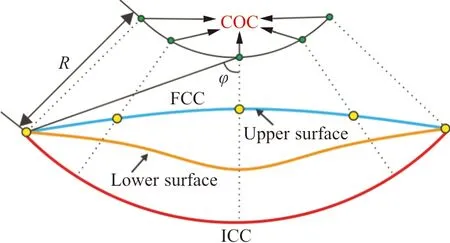
图1 新型乘波体设计示意图Fig.1 Schematic illustration of novel waverider
通过与传统曲率圆心相比,本文定义新的圆心相当于改变了同一锥型流激波上流线的位置。根据锥型流特点,当激波面上的流线起始点靠近圆锥原点时,在相同的流向距离上,流线扩张角更大,对应更大的当地出口厚度,从而可以改变乘波体的容积。基于相同的圆锥流场,采用流线追踪方法计算3个从不同径向半径前缘点出发的流线的差异,如图2所示,可以看出:半径越小对应的出口流线偏转度越大。
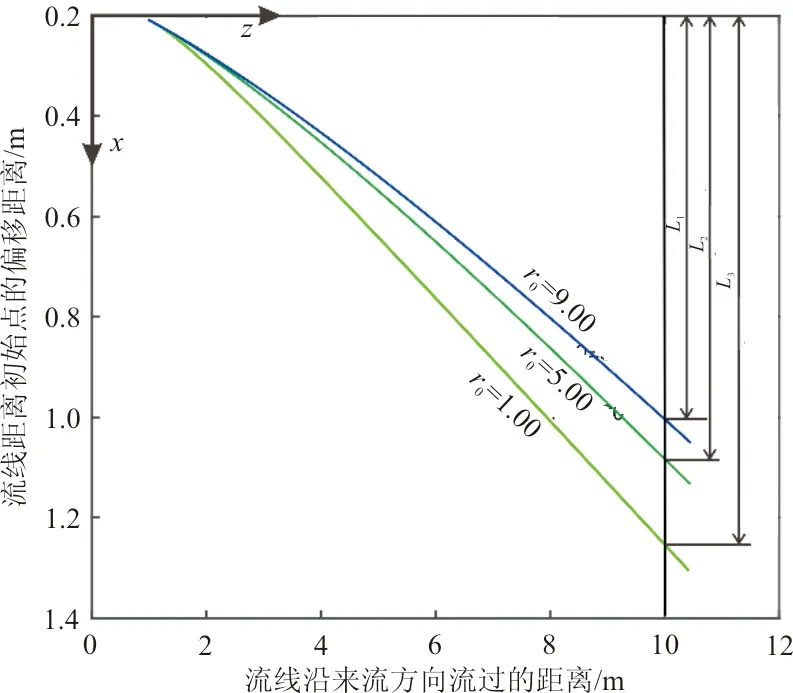
图2 前缘点径向距离对流线的影响Fig.2 Streamlines difference by different radial distance of leading points
对应于设计乘波体时,如图3所示,从A点出发的流线,当地激波半径不同时,在相同的流向上乘波体出口厚度不同,r2>r0>r1,对应CF>CE>CD。
图3 圆锥流线示意图Fig.3 Schematic illustration of conical streamlines
本文采用该方法分别设计四种乘波体:传统吻切锥乘波体、激波半径减小乘波体、激波半径加长乘波体和激波曲线为直线的乘波体,分别命名为W1、W2、W3和W4,如图4所示。
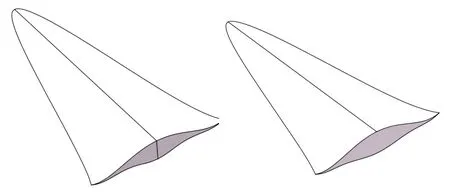
(a) W1 (b) W2
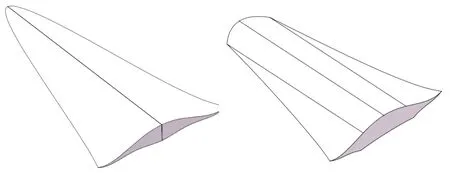
(c) W3 (d) W4
图4 不同设计方法得到的乘波体构型
Fig.4 Waverider configurations by different design methods
四种设计方法如图5所示。

(a) 吻切锥乘波体设计

(b) 激波半径减小乘波体设计
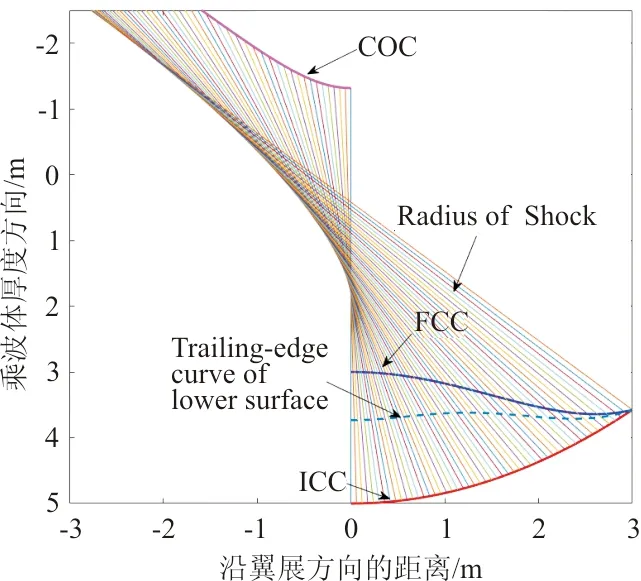
(c) 激波半径加长乘波体设计
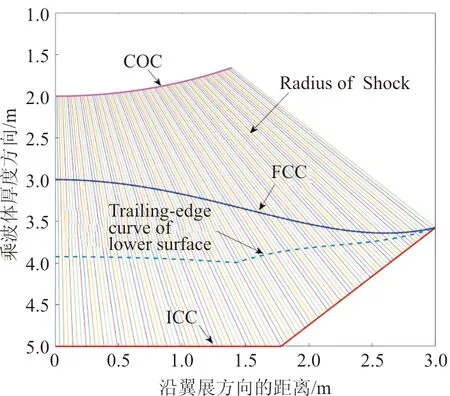
(d) 直线激波曲线乘波体设计图5 不同乘波体设计示意图Fig.5 Design schematic of different waveriders
四种乘波体的几何参数特征如表1所示,可以看出:当出口激波半径被加长时,会导致乘波体的容积和容积率降低,出口激波半径被减小则对应更大的容积和容积效率。
本文容积率的定义为
式中:V为乘波体的体积;Sp为乘波体的水平投影面积。

表1 不同乘波体的几何设计参数Table 1 Geometric parameters of different waveriders
3 数值方法和验证
SSTk-ω湍流模型是在Menter提出的标准k-ω湍流模型的基础上发展起来的,该模型结合了k-ε和k-ω湍流模型的优点,在近壁面附面层采用k-ω湍流模型,由于k-ω模型对逆压梯度敏感,能够模拟较大分离运动;在附面层外面的流场中,使用k-ε湍流模型,能够有效地避免k-ω模型对自由来流敏感的缺点。因此,SSTk-ω模型能够较好地模拟中等分离流动。其控制方程为
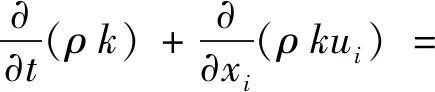
(6)
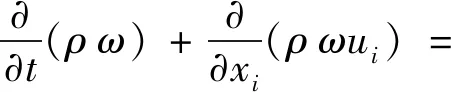
(7)
湍流粘性系数μt通过k和ω来计算:
(8)
式(6)~式(8)中其他参数的具体含义可参考ANSYS FLUENT帮助文档[18]。
N.Takashima等[19]利用MAXWARP(Maryland Axisymmetric Waverider Program)代码进行乘波体设计,得到一个优化的乘波体构型,并采用CFL3D对该乘波体进行数值分析,证明了MAXWARP在优化乘波体构型设计中的优越性。本文采用文献[19]中给出的前缘曲线生成锥导乘波体构型,并对本文的设计方法进行验证。文献[19]中乘波体的长度为60 m,飞行马赫数为6,飞行高度为30 km,基于乘波体长度的雷诺数为1.294×108。第一层网格厚度为0.000 01 m,基于单位长度雷诺数的y+小于5。
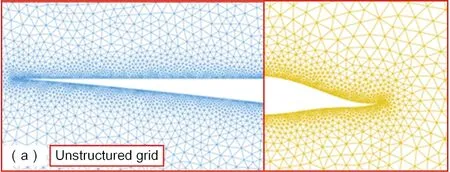
本文验证乘波体的计算区域和网格示意图如图6所示,分为结构网格和非结构混合网格进行对比验证。
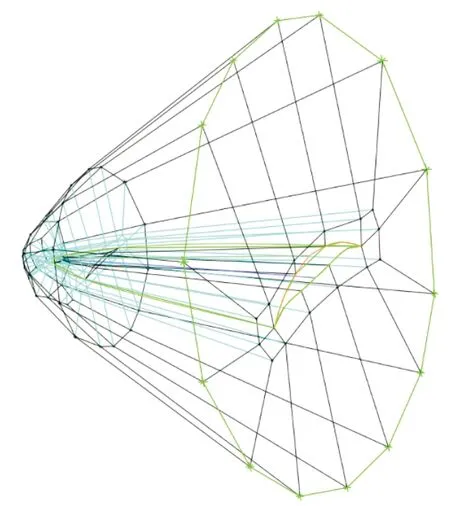
(a) 计算域与结构网格拓扑

(b) 结构网格
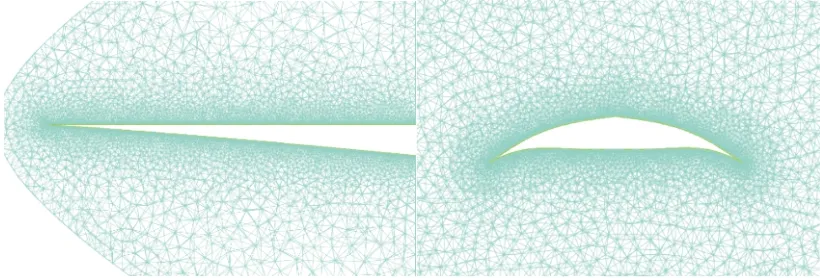
(c) 非结构混合网格图6 乘波体构型与计算网格Fig.6 Waverider geometry and computed grid
粘性条件下的网格收敛性分析如表2所示,本文计算结果均不考虑底阻对气动性能的影响,可以看出:在本文选择的网格规模内,不同网格计算结果差异性很小,为了保证精度同时提高计算效率,选择中等规模的网格进行分析。

表2 网格收敛性分析Table 2 Grid independency analysis
不同计算方法和网格对计算结果的影响如表3所示,可以看出:与文献[19]结果对比,本文采用结构和非结构混合网格都能得到较好的计算结果。
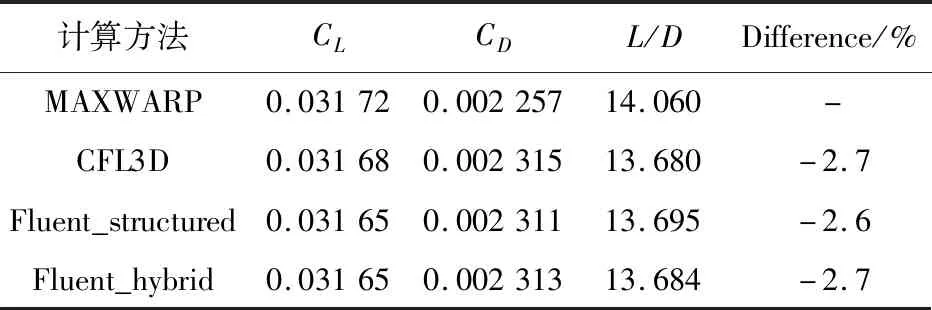
表3 不同计算方法的无粘结果对比Table 3 Inviscid results of different computational methods
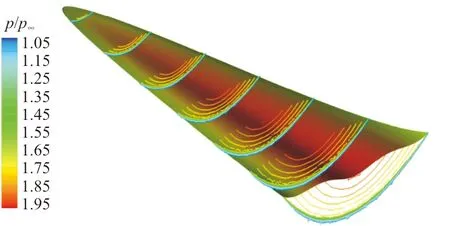
MAXWARP和Fluent计算的出口压力云图对比如图7所示,可以看出:Fluent计算结果与文献[19]结果吻合较好。

图7 本文计算与文献[19]中压力云图对比Fig.7 Pressure contour contrast between results in this paper and results from reference[19]
4 结果分析
针对设计的四种乘波体分别进行无粘和粘性数值分析,无粘计算采用非结构网格,粘性计算采用非结构混合网格。计算马赫数为6,飞行高度为30 km,来流压强为1 200 Pa,来流温度为226.5 K。采用半模型进行计算,总网格量约为200万,第一层网格厚度为0.000 01 m,基于单位长度雷诺数的y+小于5。为了更好地捕捉激波面,在无粘计算中采用自适应网格技术,计算网格如图8所示。采用压力远场和压力出口边界条件,壁面选择无滑移绝热壁面边界条件。
(a) 非结构网格

(b) 非结构混合网格

(c) 自适应网格图8 乘波体计算网格图Fig.8 Schematic diagram of the waverider computed grid
设计状态下的无粘计算结果如表4所示。
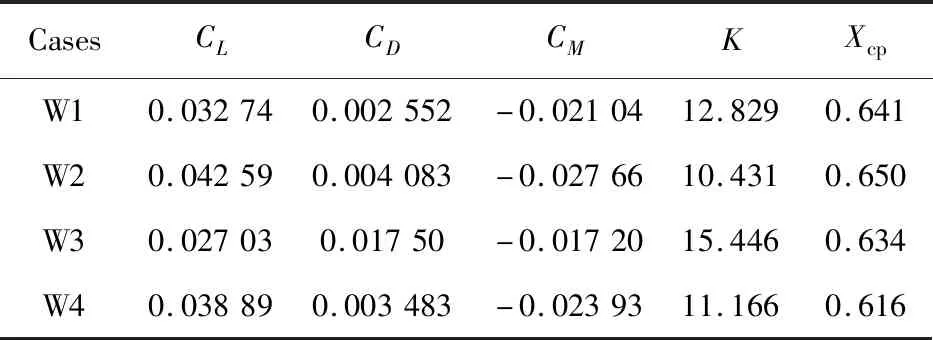
表4 设计状态无粘计算结果Table 4 Inviscid results of different waveriders
从表4可以看出:无粘条件下,W3具有最大的升阻比,达到了15.446;W2升阻比是最小的,为10.431,原因是W2的容积率是其中最大的;四种乘波体的升力系数和阻力系数也表现出明显的差异,压心的位置差异性不大,基本都是在0.63左右,因此设计状态下乘波体气动性能与设计参数的关联性很大。
设计状态下的粘性计算结果如表5所示,可以看出:四种乘波体的粘性升阻比非常接近,压心位置也基本一致;粘性升力系数与无粘基本一致,阻力系数出现明显增加;值得注意的是,虽然无粘升阻比差异很大,但是粘性升阻比差异很小;W2相比于W1,容积率增加了14.58%,升阻比只减小了4.59%。因此,从容积特性和气动性能总体来看,本文的设计方法较传统的吻切锥乘波体拥有更大的自由度,可以调节乘波体的容积效率,同时能够保持较好的乘波特性。

表5 设计状态粘性计算结果Table 5 Viscous results of different waveriders
四种乘波体在无粘条件下的截面压力等值线云图如图9所示,可以看出:在设计状态,四种乘波体都能较好地将高压区域限制在乘波体下表面,表现出很好的乘波特点。
(a) W1

(b) W2
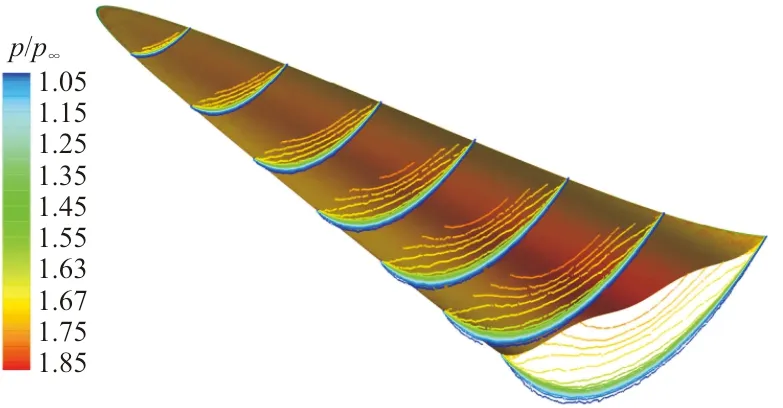
(c) W3
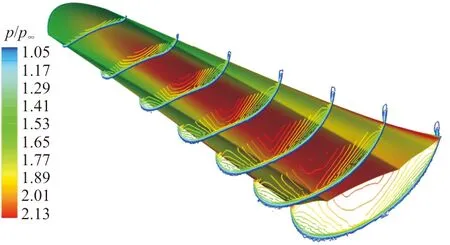
(d) W4图9 无粘条件下不同截面等压线分布Fig.9 Distribution of inviscid pressure contours at different slices
出口截面无粘和粘性压力云图对比如图10所示,可以看出:无粘条件下,高压都能很好地被限制在下表面;粘性条件下,乘波体两侧出现部分高压泄露,这是由于粘性导致乘波体前缘产生了脱体激波。
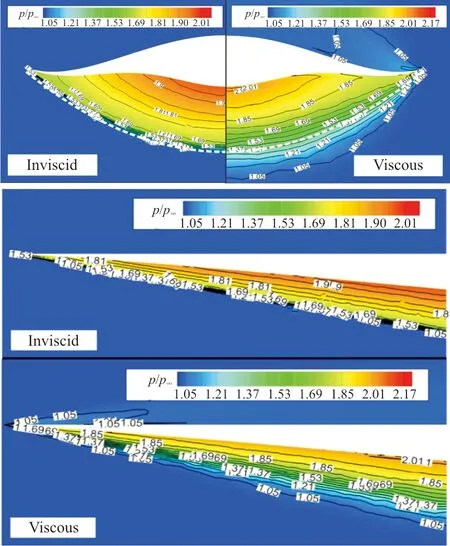
(a) W1
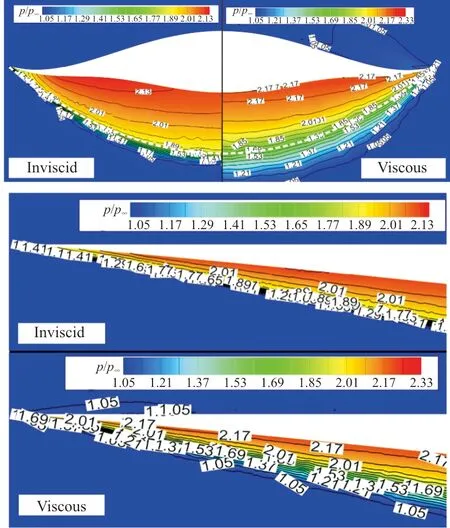
(b) W2
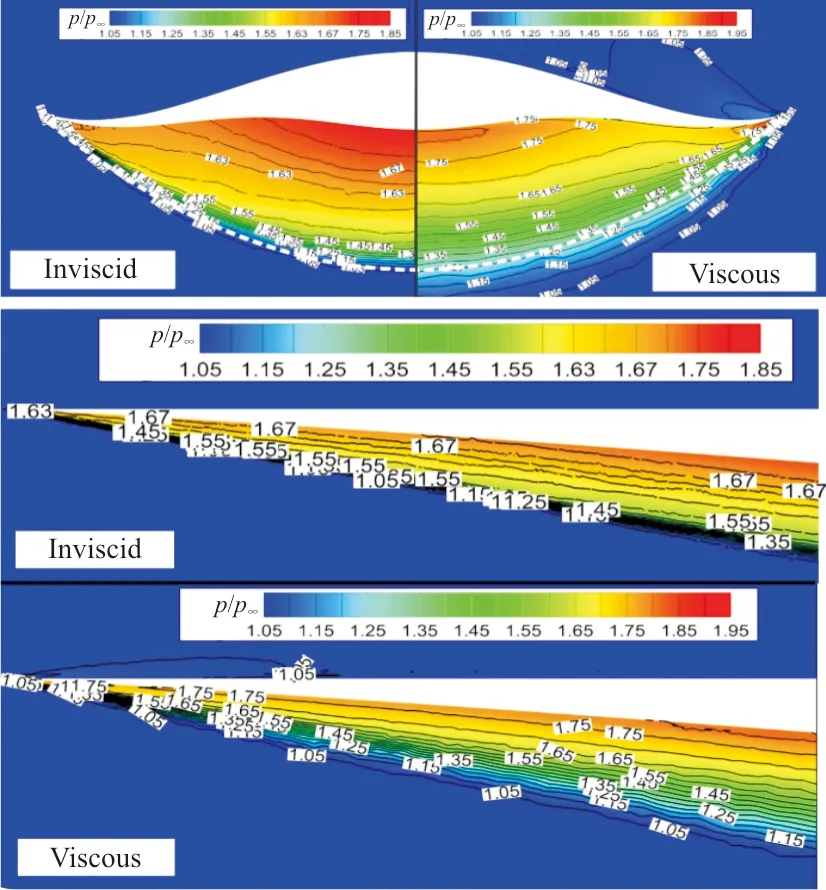
(c) W3
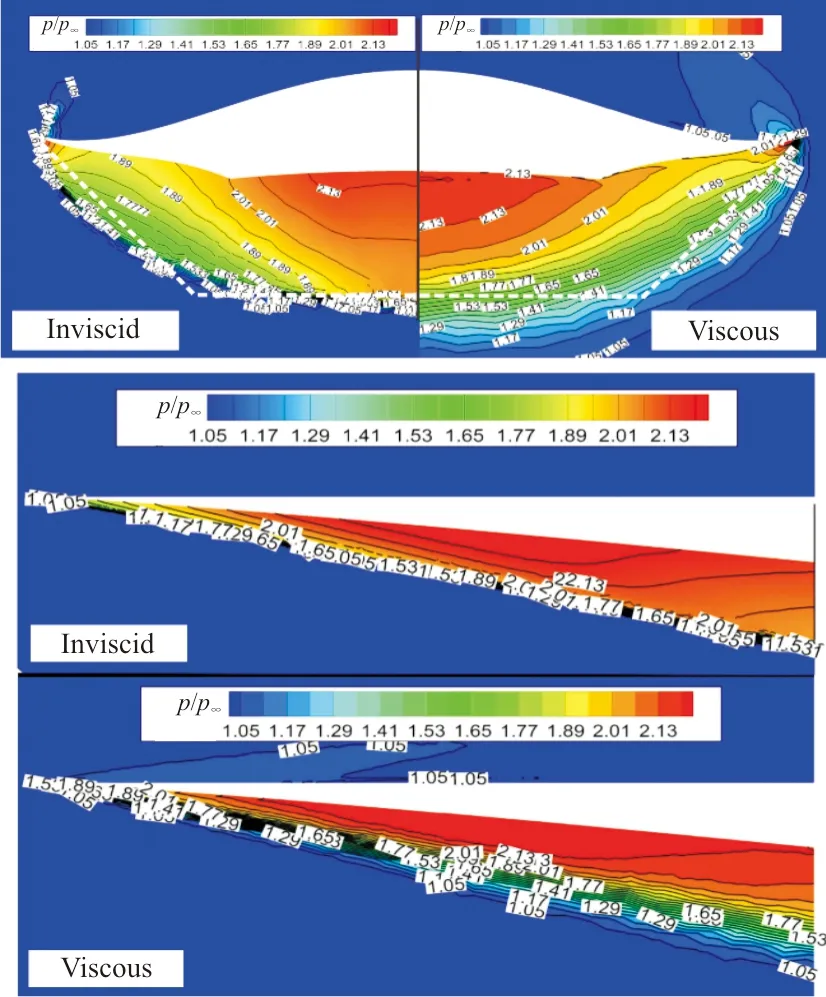
(d) W4图10 无粘和粘性出口压力云图和对称面压力云图对比Fig.10 Comparison of pressure contour of outlet and symmetry planes between inviscid and viscous results
5 结 论
(1) 在设计状态下,本文提出的新型乘波体能够得到与传统吻切锥乘波体一致的升阻比,证明本文方法是可行的。
(2) 通过改变出口激波半径,可以有效调节乘波体的容积效率,对乘波体的粘性气动性能产生很小的影响。本文所提设计方法扩展了传统吻切锥乘波体的设计空间,在相同FCC和ICC的前提下,该方法可以根据容积需求得到期望的乘波体构型,还能够通过调整参数设计不同的构型。
(3) 本文所提设计方法可以释放对ICC曲线的几何约束,通过采用直线出口激波的计算结果来看,乘波体依然具有较好的乘波气动性能。因此,本文提出的新型乘波体设计方法可以有效拓展已有乘波体设计理念,为未来更加实用的乘波体构型和高超声速飞行器设计提供参考。
