火箭发动机有遮挡情况的尾焰红外辐射计算

尹振跃，朱定强，任泓帆

(北京航空航天大学 宇航学院，北京 100083)

0 引言

火箭发动机尾焰具有高速、高温、大流量的特点[1]，会产生强烈的红外辐射特性。对于结构复杂的火箭发动机系统，其主发动机和多个姿控游机会产生多个尾流流场，这些发动机和涡轮排气出口组件等结构会对一些位置产生遮挡效应，使得该位置的辐射量数值变小，影响了整体的热流密度分布[2]。同时，由于实验测量尾焰红外辐射强度成本较高且不易实现[3]，故数值仿真尾焰红外辐射强度成为了一种成本低并且可靠的研究方式。

运用反向蒙特卡洛方法(Backward Monte Carlo Method, BMCM)的火箭发动机尾焰流场辐射特性研究起始于上世纪90年代，取得了一系列成果。H.F.Nelson[4]1992年在计算火箭发动机尾焰对发动机底部加热问题中首次提出了反向蒙特卡洛法计算模型，并通过计算结论证明BMCM可以很好地计算热辐射传递问题。D.V.Walters和R.O.Backius[5]研究了在非均匀并具有吸收、发散、散射介质中反向蒙特卡洛法的应用，其中热辐射相互作用为反向蒙特卡洛法提供了理论基础。张涛[6]的博士论文中提到了光线发射过程中遮挡判断的基本数学算法。以上研究成果为复杂有遮挡情况下的火箭发动机尾焰流场的红外辐射特性研究提供了重要帮助。

目前，针对复杂状况下尾焰的辐射特性研究并不完善，因此需要进一步研究。本文把遮挡算法的数学模型与反向蒙特卡洛辐射计算模型结合在一起，编写基于C++语言的计算机程序，研究了有遮挡情况下，火箭发动机尾焰流场的红外辐射特性。

1 计算方法

1.1 反向蒙特卡洛方法

反向蒙特卡洛法是终点开始，逆向追踪光束路径，从而确定沿路径发射的辐射能进入探测器的数量，其主要依据为辐射传递因子的互易性[7]。BMCM在处理小面元或者小立体角接收到能量辐射量问题时非常有效[8]，利用发射、反射和吸收等传递过程的概率模型，统计到达被测目标的各个体元和面元的热射线数量[9]。

如图1所示，面元i或者体元j沿着θk角方向在微元立体角dΩk发射出来的能量被面元0沿着θ角方向在微元立体角dΩ吸收的能量可以表示为

Qi→0=ΔAiεicosθkdΩkIb(Ti)Di,k0

(1)

Qj→0=ΔVjkjdΩkIb(Tj)Dj,k0

(2)

式中：kj为体元j的吸收系数；ΔAi为面元i的面积；ΔVj为体元j的体积；辐射传递因子Di,k0或者Dj,k0为从面元i或者体元j发射出来的能量沿着θ角方向在立体角dΩ内进入面元0的能量的比例因子。

图1 闭合空间内的反向光束追踪Fig.1 Backward beam tracing in closed space

若T0=Ti或T0=Tj，则面元0与面元i或体元j之间无净热交换，即Q0→i=Qi→0或Q0→i=Qi→0。

则可计算得到以下关系，即

A0ε0cosθdΩD0,jk= ΔAiεicosθkdΩkDi,k0

(3)

ΔA0ε0cosθdΩD0,jk=ΔVjkjdΩkDj,k0

(4)

上述两式即为辐射传递因子的相对性。由于传递因子只与几何形状及物性参数有关，而与工况无关，该公式在特殊环境条件下推导出来，却在所有环境下都适用。

BMCM可得到辐射能量

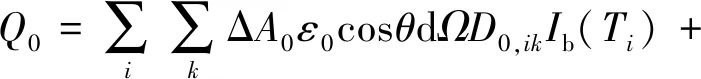
(5)

为计算辐射能量，正向蒙特卡洛法需要跟踪所有面元i和体元j发射的能量束，而反向蒙特卡洛方法只需要跟踪面元0发射的能量束即可，效率远高于正向蒙特卡洛法。

1.2 遮挡算法

本文采用逼近效果最好的三角形网格统一表示物体表面。判断线段O1mO2m与三角形Es的位置关系。如图2所示，单元Es的3个顶点为i，j，m,则

(6)

式中：AijO12，AjmO12，AmiO12分别为三角形ijO12，jmO12,，miO12的面积;ζ为判断阈值，一般取小于10-3的值即可满足计算精度。若式(6)成立，则线段O1mO2m与遮挡单Es相交。

遮挡判断时，判断式(6)是否成立，若存在一个遮挡单元Es对计算单元E1和E2产生遮挡，则两者之间辐射热流为0,并且中止其余遮挡单元的遮挡判断。

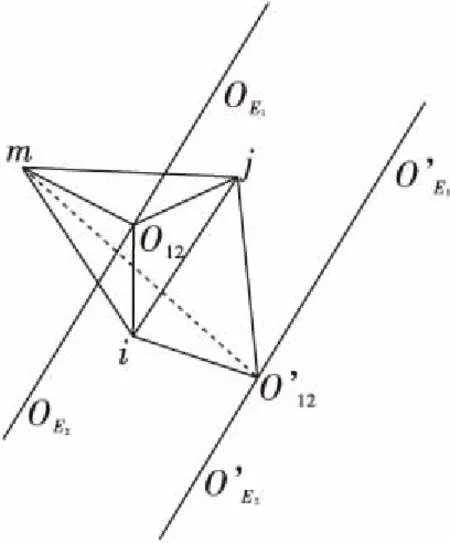
图2 线段与三角形相交Fig.2 Segments intersect with triangles

2 计算结果分析

2.1 反向蒙特卡洛方法计算红外辐射正确性

采用《传热学》[10]标准算例9-8对所编写的反向蒙特卡洛程序进行验证计算。该尾焰流场以x轴正方向为尾焰喷流方向。参数如表1所示。

表1 等温流场参数

计算得到尾焰流场圆柱侧表面的辐射强度，如图3所示。

图3 柱面辐射强度结果Fig.3 Results of cylindrical radiation intensity

圆柱侧面的总辐射热量为1.5×105W。总辐射热量与标准验证算例的数据相对误差1.06%。从柱面热流密度分布规律上来看，柱面探测面中心区域出现热流密度最大值，以柱面中心端面为中心向底面呈对称趋势减小，并且相同x截面上的辐射强度数值大小十分相近。

在圆柱流场模型x=0 m，计算得到尾焰流场底面辐射强度如图4所示。

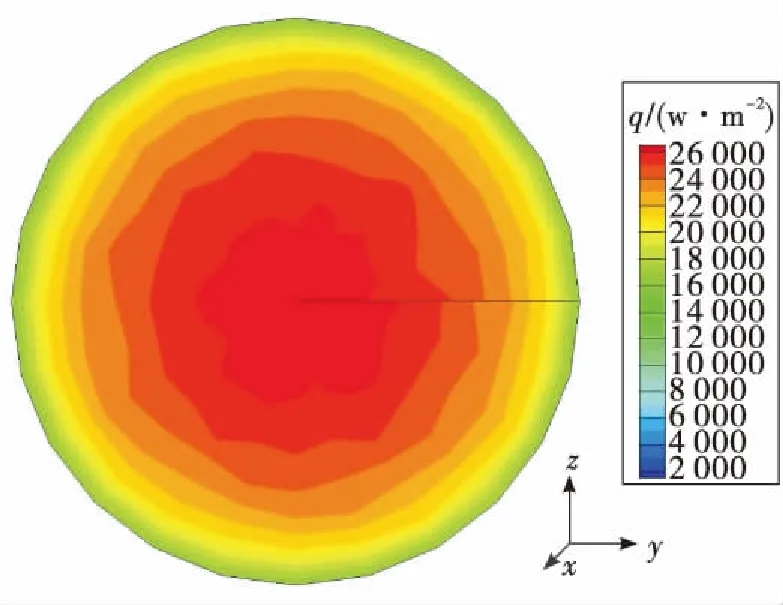
图4 底面辐射强度结果Fig.4 Results of bottom radiation intensity

底面的总辐射热量为1.8×104W，总辐射热量与标准验证算例相对误差5%。从辐射分布规律上来看，底面中心区域出现热流密度最大值，并以此为中心沿径向呈逐渐降低趋势，同心圆上的辐射强度数值大小十分相近，例题与程序计算结果如表2所示。

表2 例题与程序结果对比

综上所述，本文的辐射计算结果与教材算例相比，辐射强度分布规律符合基本理论，总辐射热量的误差在可接受范围内，可以认为本程序的计算结果是正确的。

2.2 遮挡对复燃尾焰流场红外辐射的影响

基础流场出自文献[11]，其温度云图如图5所示。

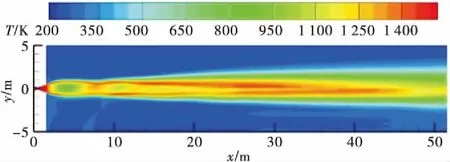
图5 尾焰流场温度云图Fig.5 Temperature cloud map of flame flow field

流场、遮挡物和探测面三者间的相对位置如图6所示。计算探测面的红外辐射并记录射线路径。结果中仅显示进入流场区域的射线，被遮挡和溢出流场等未与流场相交的射线则未显示。这样的好处是可以清楚地展示遮挡物体的遮挡效应。计算了平板、管、杆等典型的遮挡物结构时的辐射。流场、遮挡和探测面的几何参数如表3所示。计算时发射5 000条射线。

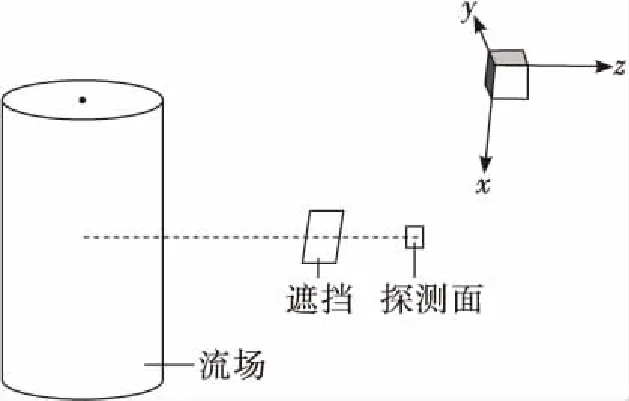
图6 流场、遮挡面和探测面三者之间相对位置关系Fig.6 Relative positional relationship among flow field, shading surface and detection surface

类别几何参数尺寸及说明流场长/m48 半径/m3下底面圆心位置原点轴线方向x轴探测面法向量(0,0,-1)计算点坐标(20,0,7)板遮挡法向量(0,0,1)中心点坐标(20,0,6.1)面积/m20.2×0.4圆柱遮挡中心点坐标(20,0,6.1)长度/m2半径/m0.05轴线方向x轴

无遮挡物体时，射线发射情形如图7所示。图中的圆柱是流场区域，射线从探测面元外法向出发，进入流场区域，最终被吸收。外法向与探测平面所形成的半球空间内，射线的分布对称于外法向，除半球空间部分低纬度的射线由于未进入流场区域没被记录外，射线充满了半球空间。符合物理规律。

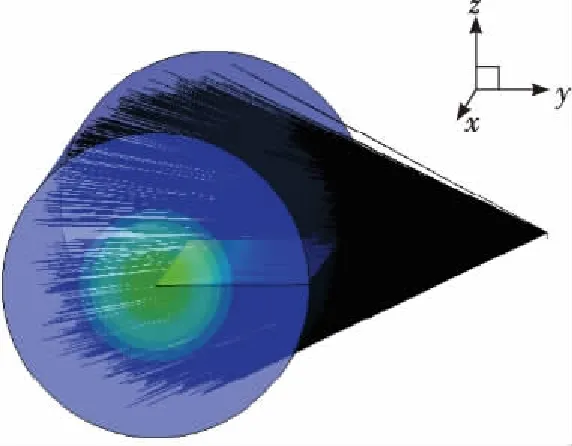
图7 无遮挡时射线发射情形Fig.7 Radiation emission situation without shielding

增加平板类遮挡，其几何参数如表3所示。结果如表4所示，射线减少18.47%，辐射强度减少24.57%，遮挡效应明显。

仅增加圆柱类遮挡，模仿真实系统的管、杆等结构。结果如表4所示，遮挡效应明显。射线被圆柱体遮挡情形如图8所示，与无遮挡情况对比，图中间部分形成一个没有射线的区域，被遮挡之后，射线无法穿透遮挡物进入流场区域。

对于上述的板和圆柱类遮挡，遮挡物的存在阻止了射线进入流场中心高温区，而辐射强度大小与温度最为相关，所以辐射强度减少的幅度要大于射线减少的幅度。

图8 射线被圆柱体遮挡Fig.8 Rays blocked by the cylinder

遮挡类别进入流场射线数辐射强度无遮挡2 1501.180 6×103(W·m-2)板遮挡1 7538.905 7×102(W·m-2)下降百分数/%18.4724.57圆柱遮挡1 9157.158 6×102(W·m-2)下降百分数/%11.4639.36

针对圆柱类遮挡，仅改变圆柱半径，所得辐射数值变化折线图如图9所示。随着圆柱尺寸变大，辐射热流密度数值逐渐减小，遮挡效应增强。该变化规律符合理论。

图9 圆柱遮挡物不同半径下的辐射强度Fig.9 Radiation intensity at different radius of cylindrical shield

针对圆柱类遮挡，固定探测面和流场位置，仅改变圆柱的位置，使得圆柱与探测面之间的距离变化。所得辐射数值变化折线图如图10中的方块点曲线。

图10 圆柱遮挡物不同位置下的辐射强度Fig.10 Radiation intensity at different positions of cylindrical shield

随着圆柱圆心y坐标增大，其距离探测面越来越近，辐射热流密度数值逐渐减小，可见遮挡效应增强。遮挡的y坐标4～6.5 m段，即遮挡距离探测面3～0.5 m段，辐射强度出现骤降，该现象原因是：① 辐射强度与温度最为相关。流场非均匀，其轴线附近是温度最高区域，随着遮挡与探测面距离越来越近，探测面发射的射线逐渐不能进入高温区，辐射强度出现骤降；② 距离对辐射骤降的影响不是线性的。以图11遮挡圆截面为例。

图11 遮挡半角变化Fig.11 Change of shielding half angle

图11中y坐标每次增加Δx,可以得到第n次的遮挡半角

(7)

设Δθ=θn-θn+1，n取0～12，得到Δθ-y曲线，如图10中三角点曲线，可见随着y坐标增大，遮挡与探测面越来越近，即n值减少，遮挡半角增幅逐渐加大，也就是遮挡效应骤增，与辐射强度下降趋势相反。直径截面规律与上述相似。上述两种因素共同作用，导致了辐射强度—y坐标曲线出现骤降。

2.3 火箭发动机推力室上方红外辐射计算

本文针对上述的复燃尾焰流场的推力室，计算了该液体火箭发动机推力室的头部上方若干个位置的辐射。此情形下，推力室作为遮挡物。推力室几何参数如表5所示。

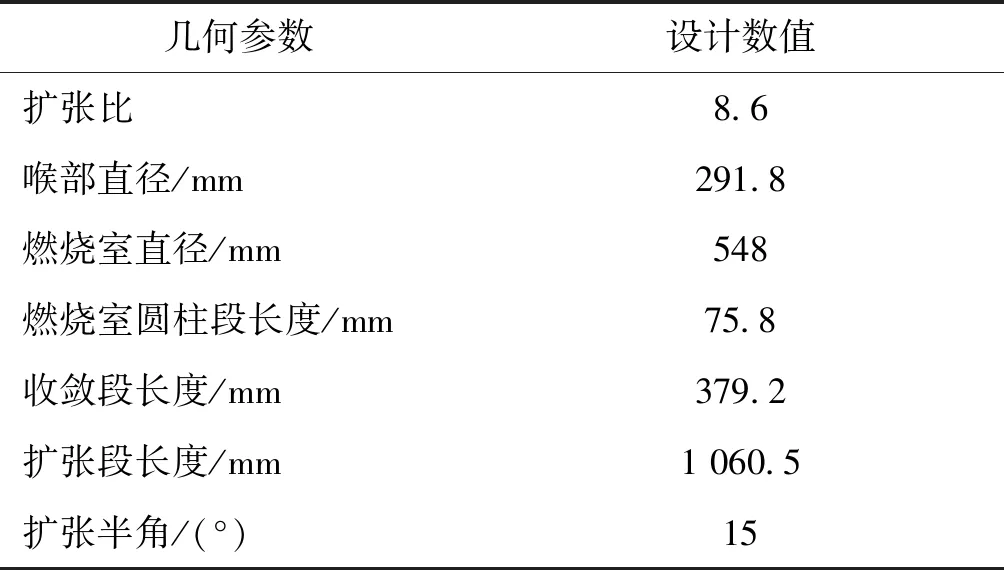
表5 推力室设计参数

采用结构化网格划分发动机结构。按照其排布规律，计算出的发动机的子平面法向量是外法向量，满足遮挡算法要求。计算射线5 000条。

3个探测面与发动机的相对位置如图12所示。探测面的法向量均是指向发动机的。

图12 3个探测面与发动机的相对位置Fig.12 Relative position of three detection surfaces and engine

对于探测面，存在发动机作为遮挡物时，射线发射情况如图13所示，可以看出射线与遮挡存在交汇处，射线被吸收，而终止行进，图13(b)发动机后出现光线缺口；其他进入流场的部分当满足公式时终止。

图13 有遮挡时探测面1发射射线情形Fig.13 Emitting rays of detecting surface 1 with shielding

探测面1、2和3计算所得辐射结果如表6所示。

表6 探测点辐射强度数值

有遮挡时，3个探测面的辐射强度数值很接近，均在3 600 W/m2；探测面2与探测面3相比，探测面2更接近推力室轴线，被遮挡程度更甚，所以辐射强度下降更多，约为28%，探测面3辐射强度略大；无遮挡时，探测面1辐射强度数值最大，约为11 180 W/m2，探测面2的辐射强度稍大于探测面3，约为5 100 W/m2和4 490 W/m2。探测面2相比于探测面3距离流场轴线更近，所以辐射强度数值更大。

3 结论

本文编写了一个可以计算流场任意处红外辐射特性的计算程序，得到了遮挡对于流场红外辐射特性的影响。获得如下结论:

1)流场的红外辐射会使附近结构表面的热流密度升高，对于结构的热环境分析很重要。对于本文中的复燃流场，表面热流密度可达104W/m2量级。

2)遮挡对于红外辐射的传输起到了阻碍作用。本文圆柱类和板类遮挡的计算结果，与无遮挡的情况对比，有遮挡的情况下红外辐射热流密度降幅可达50%以上。

3)相同条件下，遮挡物的尺寸越大，对辐射传输的削减越大；遮挡物位于探测面和流场中间时，改变遮挡物位置，使其与探测面距离逐渐变小时，辐射强度逐渐减少，并在一定范围内出现骤降。

4)对于本文采用的复燃流场主流推力室上方的红外辐射计算，大小约为3 600 W/m2。与无遮挡的情况相比下降范围为10%～70%。