圆周分段式密封动压浮起力数值仿真计算

李小芬，周 芮，涂 霆

(1.北京航天动力研究所，北京 100076； 2.西安航天动力研究所，陕西 西安 710100)

0 引言

氢氧火箭发动机氧涡轮泵动密封系统对涡轮泵设计来说至关重要，尤其是氧涡轮泵中防止液氧介质和驱动涡轮的富氢燃气相混合的氦密封[1]。氧涡轮泵氦密封是防止液氧与燃气混合的唯一屏障，是涡轮泵的关键部件[2]。以往的型号上多采用浮动环或者端面密封，而圆周分段式密封因其结构紧凑，适应高转速，泄漏量低，且具有轴向、径向补偿能力，为国外主要型号氧涡轮泵研制所青睐。

圆周分段式密封设计的关键在于计算动压槽所产生的动压浮起力。目前由连续性方程所推导出的一维公式最为简单快捷[3]；也有忽略间隙高度，通过数值分析方法求解等温条件下的二维雷诺方程来计算浮起力的方法[4-5]。但这两种方法的简化程度较高，而利用CFD三维仿真的计算方法更贴近实际流动，可以准确直观地反映密封的流动特性，同时更便于考虑由加工误差造成的密封流体膜变形对浮起力的影响。

本文利用Fluent流体分析软件来分析圆周分段式密封流场内的流动，以便得到动压槽所产生的浮起力，并综合一维计算方法和国外文献中计算结果进行比较，验证三维仿真计算方法的准确性；分析气膜厚度，动压槽深度，槽数以及加工误差导致的轴偏斜和槽偏斜等因素对浮起力的影响。

1 圆周分段密封结构和工作原理

1.1 密封原理

典型的圆周分段式氦密封的组件包括分段密封环、密封壳体、盖板和弹簧等，如图1所示。两组结构对称的分段密封环背对背放置，两环之间由弹簧预紧，贴合于密封壳体和盖板上，腔内供隔离氦气。密封环由分段的扇形密封环构成[6-7]，由外表面上的箍簧约束，装配状态下抱紧轴套，其内表面与转子外表面构成主密封面，贴合于密封壳体的端面为副密封面。

每段密封环的主密封面上都设有轴向输入槽与平衡环形槽，氦气由输入槽流入环形槽，受密封坝节流作用，减压泄出。内表面的轴向输入槽之间设置瑞利动压槽，如图2所示。瑞利动压槽为周向槽，从轴向输入槽开始，沿周向在两个轴向输入槽之间的密封面上占一定的角度，与密封内径面之间形成台阶。转轴工作时带动轴向输入槽中的介质沿周向进入动压槽，经槽根部台阶的节流，形成高压区，从而产生动压力推开密封环，使密封环处于极小间隙的浮动状态。密封内表面上的这种布置，既利用气体静力平衡原理提高了内表面压力，使其在径向压力分布上得到极大的平衡，又利用动压槽所产生的动压力，进一步克服密封环的残余外载荷，使轴和密封环维持一个微小间隙的流体膜润滑状态。

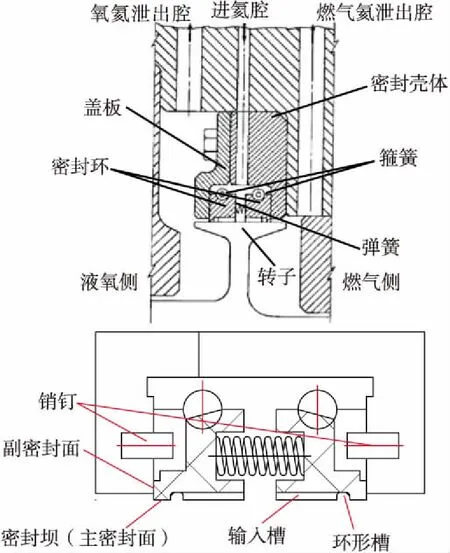
图1 圆周分段氦密封结构Fig.1 Schematic of circumferential segmented seal

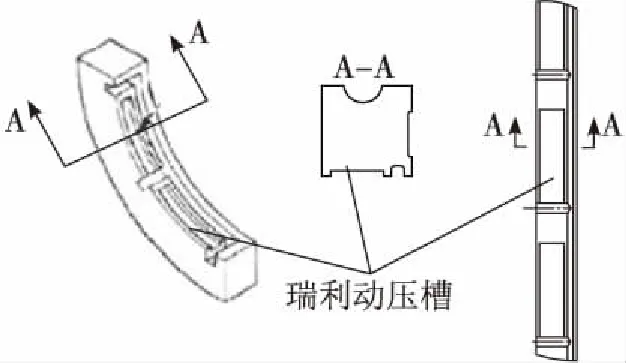
图2 瑞利动压槽结构Fig.2 Schematic of rayleigh steps

这种带动压槽的圆周分段氦密封结构在关机阶段在箍簧的压力下抱住轴，所以在涡轮泵预冷阶段氦气消耗量很低；工作阶段通过轴的旋转获得动压浮起力，使轴和密封环分离，从而可以在保持氦气泄漏量很低的同时防止密封环的摩擦磨损。

1.2 受力分析

圆周分段式密封环中每一个分段环都完全相同，分段环中每一个动压槽也是完全一致的，因此密封环的受力沿周向呈周期性分布。忽略搭接处的受力，选取其中单槽截面的简化受力分布如图3所示。上游压力作用于密封环外径的闭合力和箍簧的约束力以及副密封端面的摩擦力(以密封环呈浮起的运动趋势为例)共同形成径向闭合力。密封间隙内气体所产生的总浮起力由静浮起力、密封坝区域内气体所产生的打开力和动压槽所产生的动压浮起力组成。

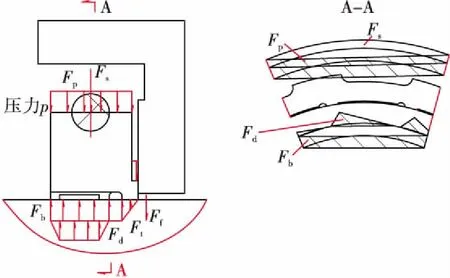
图3 密封受力分析Fig.3 Pressure profile of segmented rayleigh step seal

为了使密封环处于较极小间隙的浮动状态，动压槽所产生的动压浮起力须和径向不平衡力相等，即

Fd=(Fp-Fb-Ft)+Fs+Ff

(1)

式中：Fd为瑞利动压槽产生的动压浮起力；Fb为输入槽和环形槽内气体的静压力；Ft为密封坝区域内气体所产生的打开力；Fp为密封外载荷在外径产生的闭合力；Fs为箍簧产生的闭合力；Ff为副密封面产生的摩擦力。

为了简化计算动压槽所产生的浮起力，假设压力在槽内轴向及膜厚方向都不变，如图4所示。流过轴向环形区域的流动为Couette剪切流[8]。

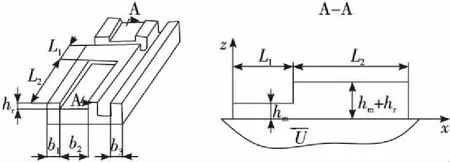
图4 一维计算模型Fig.4 One-dimentional calculation model

由连续性方程可得进出口质量流量相等，从而计算出峰值压力

(2)

式中U为轴的周向速度。

假设压力在密封间隙内呈线性变化，因此由峰值压力可以得到浮起力

(3)

2 密封环动压浮起力的三维数值仿真计算

2.1 模型及其参数

本文选用文献[3]中LE-7作为计算模型(见表1和表2)，计算其在不同膜厚和不同动压槽深度下浮起力的变化，并与文献[3]中的结果进行对比分析；之后在此基础上改变动压槽数量，考虑轴偏斜和动压槽加工偏斜等因素对浮起力的影响。

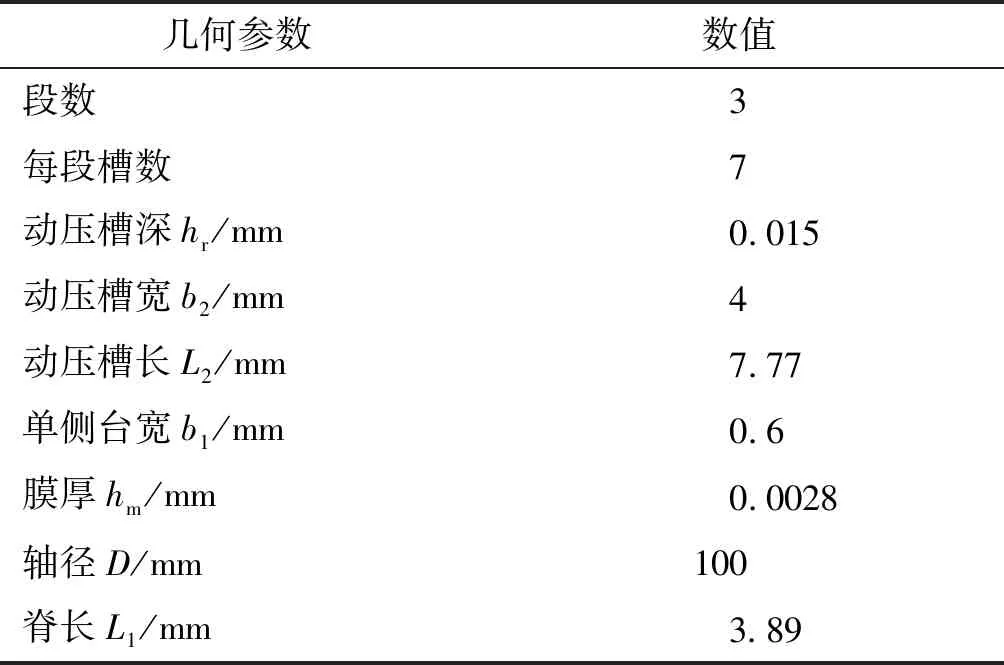
表1 LE-7模型几何参数

表2 LE-7模型工况参数

2.2 模型结构和边界条件

参考国外计算浮起力的方法，选取一个周期的动压槽、支撑瓦面和轴向输入槽为分析对象[2-3]，如图5所示。动环表面为旋转壁面，静环内径表面为静止壁面，瑞利动压槽开在静环内径面，轴向两侧一侧作为压力入口，另一侧为压力出口，气膜周向两侧为周期边界。

2.3 基本假设

为了简化计算，对密封间隙内流场做出以下假设：

1)忽略体积力的作用，如重力或磁力；

2)密封间隙内为等温环境，因此不考虑密封气体的黏度和密度随温度的变化；

3)密封气体满足理想气体状态方程；

4)流动为层流[9]，不存在涡流和湍流；

5)流体在固体界面无滑移。

2.4 网格划分

利用Gambit软件对一个周期的密封气膜进行网格划分，网格划分方式主要包括以下几个要点：

1)网格划分采用正交性好的六面体结构。

2)相比于轴向和周向尺寸，膜厚方向的尺寸小了几个数量级，为了尽量减小网格的长短边比值，同时兼顾膜厚和动压槽深的微小尺寸，将模型划分为动压槽，脊以及轴向槽3个部分分别划分网格。膜厚划分5层网格，槽深划分30层网格。

3)网格总数在90万以上时浮起力和峰值压力的变化不大，因此本文模型网格总数选择在约90万个。

2.5 求解器设置

采用基于压力的求解器隐式求解，选择层流模型压力速度耦合采用SIMPLEC算法，在较细网格划分下，方程二阶离散余量对计算结果影响不显著，压力和动量的离散分别采用标准和一阶迎风格式。

3 计算及结果分析

3.1 三维仿真与一维计算结果对比分析

圆周分段密封单个周期间隙内的三维压力场分布如图6所示，左侧为模型对称中心面上压力变化，气体流入瑞利动压槽根部后压力激增，这是由于气体进入槽后，在根部受到阻挡不断压缩形成高压。

而一维计算中忽略了密封间隙内气膜宽度方向和厚度方向的压力变化，假设压力沿周向为线性变化，如图6(a)所示。对于设计阶段，一维公式简单快捷，但在实际流动中，气体经转轴的带动流入瑞利动压槽，在槽根部受到阻挡，气体不断压缩，压力激增，压力变化并非简单的线性变化。

分别用Fluent和一维计算方法分析LE-7模型在膜厚为1.7 μm，2.8 μm和3.9 μm时，浮起力随瑞利动压槽深的变化，并和文献[3]中经过实验验证的浮起力结果相比较，如图7所示。

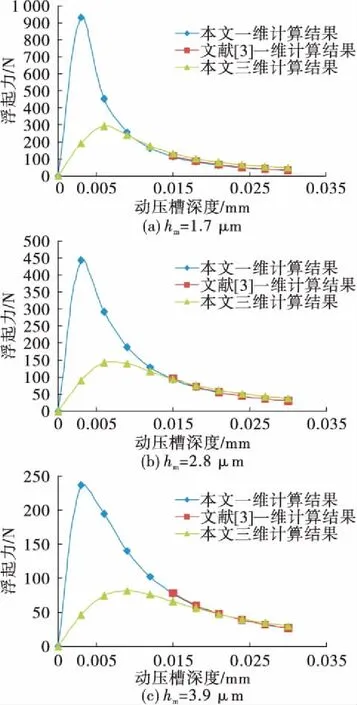
图7 LE-7不同槽深和气膜厚度对浮起力的影响Fig.7 Effect of film thickness and step depth on opening force for LE-7

由图7可以看出，浮起力随膜厚的增加而减小。而当动压槽深度大于0.015 mm时，三维仿真计算和一维计算结果相差很小，都是随着槽深的减小浮起力增大，并且和文献[3]中的数据相差小于3%。当动压槽深小于0.015 mm时，三维仿真和一维计算出现较大差异，主要原因是一维计算中忽略了气膜宽度方向的压力变化，动压槽深度越小，宽度上的密封压力变化影响越大。一维计算中随着槽深的减小浮起力不断增大，直到槽深减小至约0.003 mm时浮起力才达到最大值；而三维仿真中动压槽深约0.008～0.01 mm时，动压浮起力达到最大值，当动压槽深小于0.008～0.01 mm时，槽深越小，浮起力也越小，分析原因是当动压槽深太小或太大，都会削弱气体在高速下压缩产生的动压效应，因此，动压槽深度存在最优值，这和文献[10]中提到的结论一致。

3.2 膜厚和瑞利动压槽深度对浮起力的影响

在每段槽数为5槽下，不同槽深和膜厚对浮起力的影响如图8所示。密封气膜厚度越小，浮起力就越大。因此如果密封环在工作时密封间隙减小，浮起力就会增大，从而密封环克服闭合力浮起，密封间隙也会随之增大，而间隙增大时浮起力减小，又会使密封间隙趋于减小，最终浮起力和闭合力会保持平衡，密封间隙可以维持在微米级。

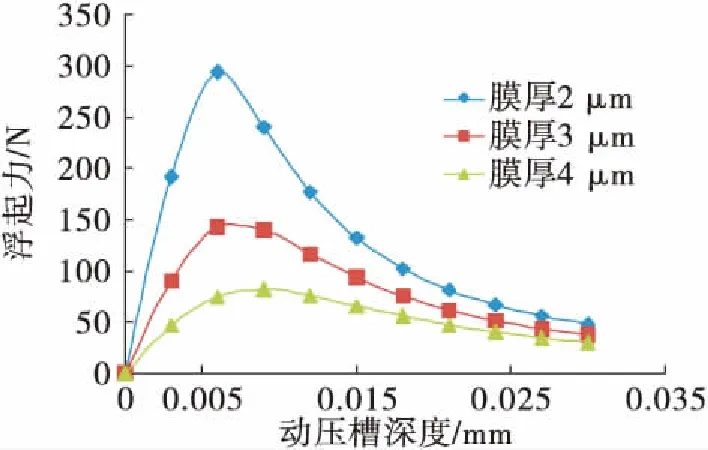
图8 不同槽深和膜厚对浮起力的影响Fig.8 Effect of film thickness and step depth on opening force

对于动压槽深度的影响，浮起力的变化并非为简单的单调函数。随着动压槽深不断增大，动压槽深浮起力先增大后降低，因此动压槽深存在最优值。不同膜厚下的动压槽深最优值存在差异，膜厚越大，动压槽深最优值越大，在膜厚为2～4 μm时，动压槽深最优值为0.008～0.01 mm。实际工作中密封环可能会发生磨损，槽深变小，浮起力增大，从而平衡间隙变大，防止进一步磨损；但槽深小于0.008 mm左右时浮起力将会减小，这样会导致磨损加剧，影响密封性能，因此在动压槽的设计过程中，槽深不宜过小。

3.3 槽数对浮起力的影响

在膜厚为3 μm时，槽数对浮起力的影响如图9所示。整体来看浮起力随动压槽深度变化趋势相同，槽数越多，浮起力峰值点对应的动压槽深度越大。一般动压槽深度的设计值为0.02～0.04 mm，允许少量磨损，可见在这个范围内，总槽数越少，浮起力越大。但是槽数越多，整环的浮起力分布越均匀，因此槽数一般在满足浮起力要求下取最大值。

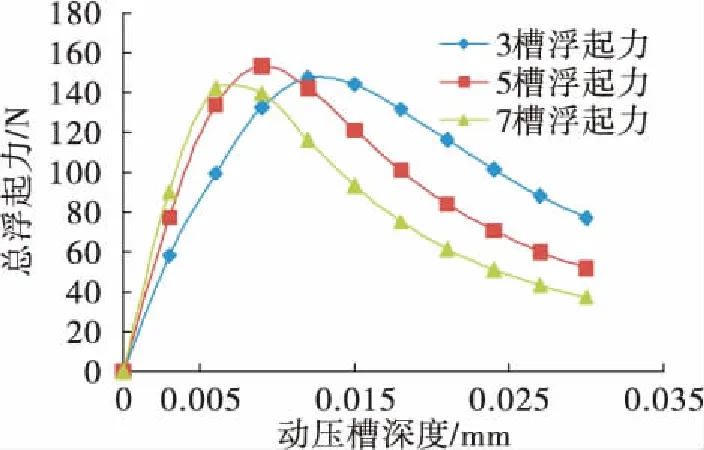
图9 不同槽数对浮起力的影响Fig.9 Effect of step number on opening force

3.4 工作时轴偏斜对浮起力的影响

在密封环的实际工作中，轴套外圆的加工误差可能导致转轴外径和密封环内径产生一定角度，考虑轴偏移对浮起力的影响，将密封气膜简化为楔形间隙模型(如图10所示)进行三维仿真计算，分别得到单段槽数为3槽、5槽和7槽的密封环随轴偏斜角度的浮起力变化，如图11所示。由图11可见，轴偏斜角度越大，浮起力越小，并且都小于无偏斜时的浮起力；同时槽数越少，浮起力下降越快。因此应尽量避免轴偏斜的情况发生。

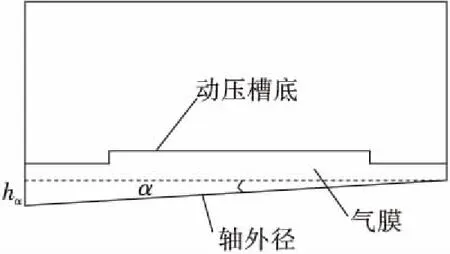
图10 轴偏斜示意图Fig.10 Schematic of shaft distortion

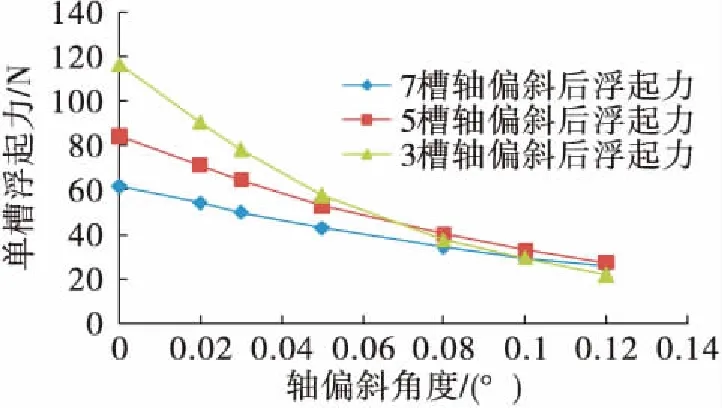
图11 轴偏斜对浮起力的影响Fig.11 Effect of shaft distortion on opening force

3.5 瑞利动压槽加工偏斜对浮起力的影响

在密封环的实际工作中，转轴可能会和密封环内径存在一定角度，考虑轴偏移对浮起力的影响，将密封气膜简化为楔形间隙模型(图12)进行三维仿真计算，轴偏斜角度所对应厚度如表3所示。分别得到单段槽数为3槽、5槽和7槽的密封环随轴偏斜角度的浮起力变化，如图13所示。由图13可见，轴偏斜角度越大，浮起力越小，并且都小于无偏斜时的浮起力；同时槽数越少，浮起力下降越快。因此工作时应尽量保证副密封面的平面度，避免轴偏斜的情况发生。

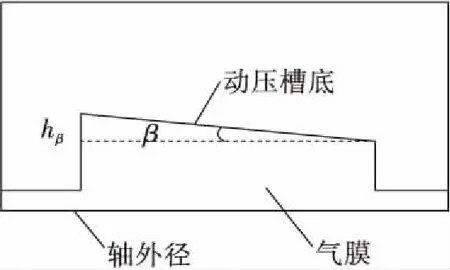
图12 槽偏斜示意图Fig.12 Schematic of Rayleigh step distortion

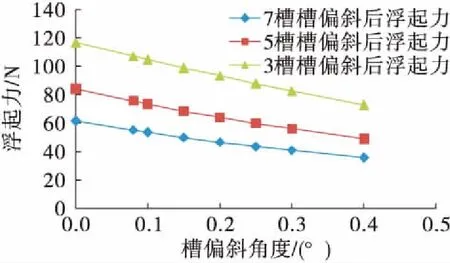
图13 槽偏斜对浮起力的影响Fig.13 Effect of Rayleigh step distortion on opening force

4 结论

本文针对氢氧发动机氧涡轮泵中的圆周分段密封进行了数值仿真，获得了动压槽所产生的动压浮起力，并得到以下结论：

1)对于圆周分段式密封动压浮起力的计算，三维仿真和一维计算方法在动压槽深度大于0.015 mm左右时结果基本一致，并与文献中结果相差小于3%；当槽深小于0.015 mm时，三维仿真与一维计算结果相差较大，因此当槽深小于0.015 mm时，不适合采用一维计算。

2)当动压槽深约为0.01 mm时，浮起力达到最大值。当槽深大于0.01mm时，浮起力随槽深的减小而增大；当槽深小于0.01 mm时，浮起力随槽深的减小而减小。而密封浮起力随气膜厚度的增大而减小。在实际工作中，密封环可能会发生磨损，槽深变小，浮起力增大，从而平衡间隙变大，防止进一步磨损；但槽深小于0.01mm左右时浮起力会减小，这样会加重磨损，影响密封性能，因此在设计时动压槽深度不能太小。

3)槽数越少，浮起力峰值对应的槽深越大；在大于峰值点的范围内，槽数越少，浮起力越大。

4)轴偏斜角度越大，浮起力越小，且槽数越少浮起力减小得越快。

5)动压槽底偏斜角度越大，浮起力越小。