“简”去繁琐 相“约”思维

摘   要：数学课堂应该是追求简约的课堂。简约设计教学环节，才能让课堂教学清晰可见;简约设计教学问题，才能让核心问题提领教学;简约设计教师语言，才能让学生站在课堂中央。立足简约教学环节的基础，凝练教学中的核心问题，减少教师的语言输出，以引导学生深度地思考，提升数学思维品质。这样的课堂才是“学为中心”的课堂，才是使学生的思维不断拓宽与深化的课堂。

关键词：小学数学;简约课堂;教学环节;课堂问题;教师语言

中图分类号：G623.5   文献标识码：A    文章编号：1009-010X（2019）19/22-0049-04

谈及数学思维品质与关键能力，史宁中教授指出，数学教育的终极培养目标是，“一个人学习数学之后，即便这个人未来从事的工作和数学无关，也应当会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界。”

数学课堂教学的时间是有限的，如何在有限的时间里最大限度地促成学生数学思维能力的提升，是每一位数学教师所面临的重要课题。基于此，我们在数学课堂中进行了一些有意义的教学尝试，提出了简约课堂的教学理念，立足简约教学环节的基础，凝练教学中的核心问题，减少教师的语言输出，以引导学生深度地思考，提升其数学思维品质。

一、简约设计教学环节，让课堂教学清晰可见

在实际教学，尤其是一些公开教学中，教师为了让数学课上的更精彩，会设计诸多细致的课堂教学环节或活动，整节课按部就班的围绕着预设的环节或活动开展教学，课堂表面上看起来热热闹闹，学生的参与热情极高，但是静下来思考，这样的课堂能给學生思维带来有效的提升么？

以六年级“百分数的应用（一）”为例。本节课的目标有两点，一是在具体情境中理解“增加百分之几”或“减少百分之几”的意义，加深对百分数意义的理解;二是能计算出实际问题中“增加百分之几”或“减少百分之几”，提高运用数学解决实际问题的能力，体会百分数与现实生活的密切联系。为此，我们设计了如下教学环节：

第一，创设情境，提出问题促使学生深度思考。基于科学中水的三态变化，我们创设了“水结成冰”的生活情境，并鼓励学生结合百分数自己提出问题：45立方厘米的水结成冰之后体积约为50立方厘米，冰的体积比原来水的体积增加了约百分之几？随后，引导他们理解题意、深度思考问题、分析问题并解决问题。

事实上，当教师相信学生并能给予他们足够的时间后，学生完全可以通过独立思考、合作交流的方式得到正确解决问题的方法，还能利用直观的线段图给出充足的解释与说明。

第二，引出矛盾，辩证思考促使学生内化知识。在上一个问题的基础上，顺势引出问题：冰的体积比原来水的体积约增加了11.1%，也就是说原来水的体积比冰的体积约减少了11.1%？这时，班级出现了一些不同的声音。我们并没有直接给出结论，而是继续留给学生足够的时间，让他们自主分析，得出结论。

在这个环节中，学生不仅通过运算解决了矛盾，还发现问题的关键在于基准量的变化，并由此得到计算“增加百分之几”或“减少百分之几”问题的一般方案，即增加（或减少）的量除以基准量，让知识进一步得以内化。

如上的教学环节设计达成了课堂的教学目标，更重要的是简约了环节的设计，不仅让课堂教学更加清晰、明了，也将教师解放了出来，能够更好地关注学生学习活动，了解学生的学情变化，便于随时调整和改进教学。也能使得学生深度参与课堂，去充分思考问题、分析问题和解决问题，内化知识。

二、简约设计教学问题，让核心问题提领教学

思维的起点在于问题。好问题不仅可以有效地激发学生的求知欲望，更为重要的是可以引领课堂教学不断深入，促使学生更深度地思考问题。问题不当也会使课堂走入误区，比如有的教师在课堂上不断提出繁多琐碎的问题，试想这样的课堂问题如何能有效？如何促使学生深度地参与思考？好的教学问题我们认为需要具备以下特点：

（一）核心问题是有深度的好问题

好问题具有深度指向性，能引导学生逐步达成学习目的。具有一定深度价值的问题才能引发学生深入地思考，在认同与反思中解决问题，提升能力。所以，好问题能使学生静得下来，钻得进去，用自己的思维拨开迷雾。

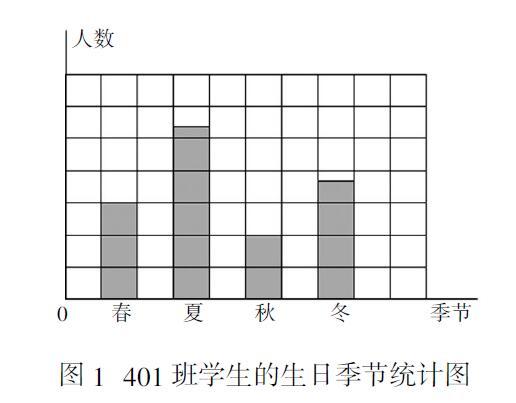
以四年级数学“认识条形统计图”为例。我们按照班级42名同学的生日，绘制了“401班学生的生日季节统计图”（图1）。依据条形的长短，可以清楚地看到401班夏季过生日的同学人数最多。我们提出了“夏季过生日的具体有多少人？说一说你的想法”这样一个问题。

生1：我想夏季过生日的同学应该是16人，因为（一直未说出）……

师：想的没错，就是16人，能说说你的想法吗？

生2：因为夏季占了5格又多出了约1/3格，所以应该是3×5+1=16。（大部分同学点了点头）

师：你这叫先入为主。在你心里是不是已经认为纵轴的1格就是代表3个人，所以才有这样的结果？但实际我们还并不知道这1格代表几个人。

（生2点了点头，坐下了）

生3：老师，我们可以这样想：假如纵轴的1格表示1人，但条形统计图中夏季的上方不满1格，人不可能有半个人，所以1格不能表示1人;假如1格表示2人，那么每1格应该都是平均分，但夏季的上方的那1格显然不是平均分的，所以也不对;再假如这1格表示3人，夏季上方的1格好像刚好约占1/3，所以我认为纵轴的1格就是代表3个人，夏季过生日的同学就是16人。

师：哦，按照你的思路老师这样想，你听听对吗？假设纵轴1格表示9人，夏季最上面1格约占了1/3，就是3人，还有5个满格是45人，这样夏季过生日的同学就是45+3=48人了，但 401班有这么多的同学吗？

（生3摇摇头）

生4：在统计图中，夏季上方的1/3格和冬季上方的2/3格能拼成1个满格，这样就一共有14个满格，我们班共有42人，用42除以14就是1格的人数了，所以纵轴1格表示3人。

师：太精彩了。

设计思考：如果只有“哪个季节过生日人数最多？”答案显而易见，学生也就失去了探索的积极性。为此，我们结合“1格代表多少个单位”的思考，设计了“夏季过生日的有多少人？”学生显然不可能直接知道401班夏季过生日的具体人数，这就促使他们必须进行深入地思考或交流。所以，有的学生通过直观感觉进行猜测，有的学生利用“假设——矛盾”的论证法进行思考，最终在联系实际（401学生总人数）的基础上，进行推理，建立了纵轴“1格代表3个单位”的统一认识，解決了问题，更是提升了学生的思维能力。

（二）核心问题是有宽度的好问题

课堂中所设计的问题指向性太明确或者方法太专一，无形之中也就让学生的思维更固化或者更单一。好问题也应该是开放性的、有宽度的核心问题，这样更益于学生不断探索，在寻找更合适的方案中优化思维，提高自身的认同感和自信心。

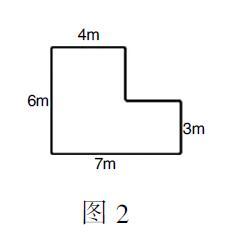
以五年级“组合图形的面积”为例。我们构建了李老师家客厅地面（图2）铺木地板的情境，提出核心问题“你能帮老师算出需要购买多大面积的木地板吗？”引导学生进行“画一画”的活动，并思考出尽可能多的解决方案。

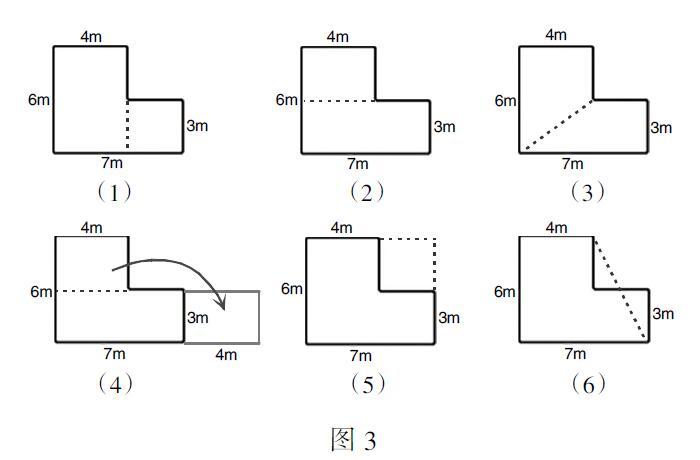
生1：我有两种办法，第一种是沿这条线将这个组合图形分成1个正方形和1个长方形（图3-1）;第二种是沿这条线把它分成了2个长方形（图3-2），分别求出基本图形的面积，加一起就可以了。

生2：我有不同的方法，可以沿这条线将它分成2个梯形（图3-3）。

师：同学们的解决方案可真多呀，看来你们都进行了认真地思考。我刚才看到还有一些更巧妙的方案，请他们也来说一说。

生3：请大家看，我是这样做的（图3-5），给它补1个正方形后变成了1个大的长方形，用长方形面积减去正方形面积就可以了。

师：大家觉得这个方案，怎么样？

生：很好，它把不规则的图形变得规则了。

师：嗯，老师很喜欢“规则”这个词，谁能说一说，什么是不规则图形，什么又是规则图形呢？

生4：组合图形就是不规则的，基本图形就是规则的。

师：（提议给他掌声）还有不一样的方法吗？

生5：（图3-4）我是沿着这条线把原图分成了2个长方形，正好它们的宽是相等的，所以，我再把上面的长方形移到下面这个长方形的右边，拼成了1个大的长方形。

师：我真敬佩你大胆尝试的创新精神，非常巧妙，而且计算简单。

师：可是，如果题目中不是6cm，而是7cm，这个方案可行吗？

生：我认为不能用了，那样分成的2个长方形宽不一样了，也就不能拼成1个大长方形了。

师：非常好，你的观察很准确。这告诉我们，在以后的学习中一定要根据题目的条件灵活选用不同的方案，可不能死搬硬套哦。

师：老师也有一个方案（图3-6），你们看看，可行吗？

生6：（上台展示）可以，您是想将下面这小三角形剪下来，移上去，把原图变成了一个直角梯形。

师：太棒了，你一下就点中了方案的关键。

设计思考：如果一个问题，只让学生利用一种解决办法，久而久之学生的思维就会形成定势，也懒于更深入地思考。这节课的情境问题设计非常简约，目的不在于计算，而是引导学生发现和体会解决问题方法的多样性。教师要引导和鼓励学生从不同角度思考问题，这是对学生思维能力的一个挑战。教学中，很多学生是能够利用四至五种方法来解决问题的，而且能够清晰地表达自己的想法与思考过程，基本达到预期的学习效果，再加上教师提供的解决方案，更能进一步拓宽学生的思维。

好问题就是核心问题，核心问题就是有深度也有宽度的好问题。这样的问题才能有效地提领课堂教学，规范教师的问题意识，同时，在师生的思辨中衍生出更多的生成性问题，助学生有更多的发现与提升，使其真正思考。

三、简约设计教师语言，让学生站在课堂中央

教师的角色定位已变为学生学习的引导者或合作者，也就是说，课堂的主角不是教师而是学生。那么怎样让学生成为课堂的主体，能够自信地站在课堂的中央呢？为了达到这样的转变，有一些学校严格分配教师在课堂的参与时间，取得了一定效果。但是课堂时间的占有量只是侧面体现谁位于主体地位，并不是最核心的表现，关键在于课堂中教师对学生的信任，而这种信任最直接的体现形式就是教师不说话或者少说话。我们都清楚，传统课堂中，教师在课堂就是不停讲话，或是讲解习题、或是分享经验、或是总结规律等等，总是以更多的“说”体现教师的存在。所以，让学生成为课堂的主体应该从教师的课堂语言入手，简约教师的课堂语言，从“教”到“学”的转型，就是让学生走向课堂的中央。

简约教师语言可以从三个方面着手。一是简约讲解过程，遇到问题或者困难，教师不急于“出手”，更多地去引导学生分析问题，协助学生深入思考，以合作者的身份参与交流，让学生在自主解决问题的过程中真正理解问题，从而解决问题;二是简约经验分享，不以“过来人”的身份谈学习知识的经验，而应该重视引领学生参与，让学生在体会中发现与成长;三是简约规律总结，不以“审判长”的身份对知识或问题给予定性的判断，而应该携同学生一起积极的去发现、去梳理归纳，让其从繁琐到简单的学习过程中提升学习能力、学会成长。只有教师课堂语言简约了，学生所拥有的时间和空间才会变多变大，才可能成为课堂中央的那个人。

综上所述，数学课堂应该是追求简约的课堂。要简约教学环节，学会筛选，让课堂教学脉络更清晰;要简约课堂问题，用宽度与深度并举的核心问题提领课堂，引导学生进入真实学习状态;要简约教师语言，切忌言之无物，哗众取宠，旨在更有效地引导与点拨，让学生真实地享有课堂。总之，简约的课堂才是“学为中心”的课堂，才能让学生相约数学能力之“核”，让思维不断拓宽与深化。

参考文献：

[1]史宁中.学科核心素养的培养与教学——以数学学科核心素养的培养为例[J].中小学管理，2018，（01）：35～37.

[2]郑毓信.小学数学教育的“别样研究”[J].小学教学（数学版），2018，（11）：15～18.

[3]李小强.大环节视角下小学数学课堂教学的实践与思考[J].云南教育（小学教师），2017，（11）：4～5.

[4]李小强，张亭亭.聚焦核心问题，发展数学思考[J].教育实践与研究（小学课程版），2018，（7）：37～40.