“问源”数学的教学研究与实施策略

刘秀妹

（尤溪一中文公分校，福建 三明 365100）

近年来，尤溪县一批骨干教师进行初中数学课改模式探索，在实践中总结创建了初中数学“五学”课堂教学的课改模式。“五学”课改模式是课堂由“导、探、研、比、评”五个环节展开教学，每个环节是围绕怎样指导学生的“学”这一核心展开教学，即“目标导学、自主探学、合作研学、展示比学、检测评学”，真正落实课堂为“学堂”。虽然该模式已在县内各中小学进行推广，但许多课改教师只是模仿了“五学”教学模式的“形”——“五环节”教学，未能准确地把握“五学”教学模式的“神”——“问题导引”贯穿教学始终。所以，笔者针对课改实践中的问题，在课题研究中形成了“问题导引——探究数学的生长之源”的教学主张，即“问源”数学的雏形。

一、“问源”数学的提出与内涵

1.“问源”数学的提出

“问源”数学是对“问题导引——探究数学的生长之源”这一教学主张的概括，也是受尤溪理学大师朱熹《观书有感》中“问渠那得清如许，为有源头活水来”的诗句启发而总结，这两名诗词的原意是要问池塘里的水为何这样清澈，是因为有永不枯竭的源头源源不断地为它输送活水；比喻意是必须要有那永不枯竭的源头源源不断地输送“活水”，才能获得不断更新和发展的新知识。新知的“活水”源头就是“问”。“学问”，“学”中“问”，“问”中“学”，才能获得真知，正所谓“乐求知、善寻问，方能水活源清”。

2.“问源”数学的内涵

“问”主要指“问题驱动、问题导引、发问与追问”等，即：教师的教学采用问题驱动与问题导引的方式引导学生自主探究式进行学习，克服传统教学中学生不会发现问题与提出疑问的弱点，引导学生发现问题、提出问题，师生共同不断地追问与反问，从而解决问题。

“源”主要指“起源、来源、根源、缘由”等，即：发现问题的缘由，新知生长的旧知来源，解决问题的方法源头。

“问源”数学指“寻根问底、追根溯源、问清源（缘）由"，即：借助问题导引进行追根溯源探究数学知识的生长之源。数学的教与学都是需要寻根问源多向探究，弄清知识的来龙去脉，因而“问源”数学教学主张体现了数学课堂实际需求，促使学生对数学知识由单纯“工具性理解”转变为“关系性理解”与“结构性理解”，“问源”数学的出发点是“问”，落脚点是“源”；“问”是关键，“源”是核心。

二、“问源”数学的依据与实施

1.“问源”数学的依据

“问源”数学这一教学主张提出的依据是皮亚杰的建构主义理论和数学学科独特的内在逻辑。因为数学每个新知识基本上是建立在相关类似的旧知基础上，经过综合加工建构新知。所以，教师在教学中只要找准新知的“生长点”即“知识源点”进行类比教学，利用旧知识生长新知识，利用旧知识解决新问题，就能达到触类旁通和举一反三的效果。

人教社主编章建跃博士在《数学教育随想录》中说：“理解数学有‘知其然，知其所以然，知何由以知其所以然’三重境界。”意思是在数学学习探究新知时教会学生发现问题、提出问题，在分析问题时进行寻根问底，问清弄明数学知识与问题是什么、为什么和如何思考的三个层面问题，探究数学知识的生长之源，从而解决问题。“问”数学之“源”，“活”数学之“水”。

2.“问源”数学的实施

遵循符合学生认知和思维活动的规律，以知识的层次性与逻辑性为主线，把教学内容问题化，串成问题串（问题链或问题组），导引学生探究数学知识的发生与发展，实现以问题为“导向”，以问题为“引子”，引出目标、引发思考、引导探究、引出思维的源头。问题成为教学的开端，问题成为教学的主线，问题成为教学的归宿。

三、“问源”数学的教学实例

以初中代数中的《一元二次方程》的《用配方法求解一元二次方程》为例进行说明。

1.目标导学问题导引，体验“问源”的类比方法，获得新知生长的旧知来源

（1）温故知新：先举例说明什么是一元二次方程，再回顾上节课中学习用夹逼估算的方法求“梯子底端滑动的距离x(m)满）足方程x2+12x-15=0”的近似解的方法步骤，说说这种方法优缺点，有更好的方法求出方程精确解吗？

（2）提出问题串：

①若一个数x的平方等于5，则这个数x是多少？若把5改为0，则这个数x是多少？若把5改为-5，则这个数x是多少？你是怎么求出数x的，用到什么知识？

②式子x2=5叫什么？求出的数x怎么称呼？求出数x的这个过程叫什么？

③若一个数x与2和的平方等于5，则这个数x是多少？怎么求解？用什么方法？

④请把方程（x+2）2=5化成一般形式，并写出它的每一项系数。

⑤你会解x2+4x—1=0方程？说明你的思路，并给这种方法起个名称。

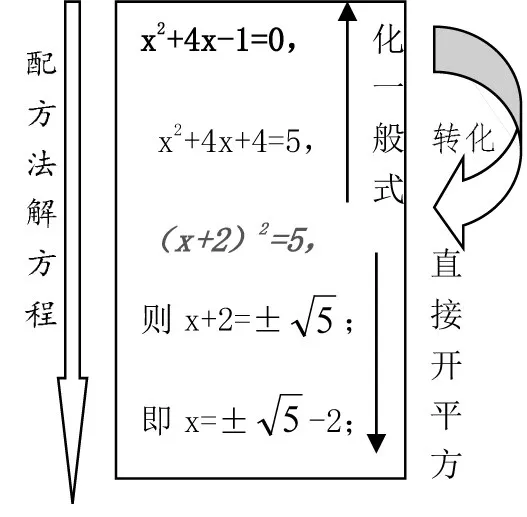
（3）导出课题与目标：课题《配方法解一元二次方程（第1课时）》的学习目标“探索用配方法解一元二次方程的方法、步骤，体会其中的数学思想”。

设计意图此例：先通过以问题的形式引导学生复习回顾，体会用估计法较麻烦，激发学生探究新方法的求知欲望，达到温故知新的目的。再利用问题串导引回顾“平方根与开平方、解方程与方程的解”的区别与联系，而后从x2=5导引到（x+2）2=5解方程，启发感悟用类比的方法与换元的思想，为探究新知“配方法”作好铺垫。而后复习方程（x+2）2=5展开的一般形式，再提出问题如何解方程x2+4x-1=0，从而让学生深刻体会其中的转化过程，体现知识的生长、发生与发展过程。本环节教师利用问题情境与问题串进行层层深入的问题导引，由新旧认知冲突，“问”出新知的生长源头，“导”出学习任务与目标，体验“问源”的类比方法，获得新知生长的旧知来源。

2.自主探学导引问题，经历“问源”的探究过程，获得新知发展的方法源头

（1）寻配方——配成完全平方式：

（2）用配方——解下列方程：

设计意图：教师设置有梯度且能针对教学重难点问题，让学生带着这些问题独立自主地进行探究性学习。根据学生学习能力的不同布置不同的学习任务与要求（中下生完成解方程①②两个小题，中等生完成解方程①—④四个小题，优秀生完成解方程①—⑥六个小题），体现分层次教学与因材施教。自主探究中经历了对数学新知学习的自我理解与自我领悟，就是经历了“问源”的探究过程，获得解决问题的方法源头。

3.合作研学导引问题，提升“问源”的数学思维，获得解决问题的本质根源

（1）寻配方中的填空有什么技巧？左边填的数与什么有关？什么关系？

（2）用配方法解下列方程步骤有几步？每一步分别是什么？关键步骤是什么？易错点是什么？用到什么数学思想方法？

（3）一元二次方程的解有几种情况？举例说明.

设计意图：通过交流概括出配成完全平方公式是配方法的本质，把一元二次方程二次项系数化成1之后，方程左右两边同时加上一次项系数一半的平方是配方技巧，移项、配方、变形、开方、求解、写解是配方法解方程的六个步骤，关键步骤是配方，降次与转化是配方法中主要用到的数学思想，配方法易错点是移项忘变号、配方时右边忘记加上与左边一样的数，开平方时忘记了“±”。这些结论的得出来源于层层递进、步步深入的问题导引，学生在实例分析中的亲身感受拾级而上、步步登高的感觉，在建构知识的过程中形成发现问题、分析问题与解决问题的能力，并培养学生应用数学意识，提升“问源”的数学思维，找到解决问题的本质根源。

四、结束语

“问源”数学的教学主张的教学实践构想是以“五学”课堂教学模式为载体、以问题导引为主线，构建适合本土教学原生态的有效的教学策略，它促使学生在设问与反问中进行合作交流，学会思考与探究，提升学习能力，促进课堂教学的实效。在教学中通过找准新知的生长点进行问题导引思维源头的数学学习，让数学的学习经历“问源”的探究过程，体验“问源”的类比方法，收获“问源”的推理新知，提升“问源”的数学思维，使数学学科核心素养得到落实。