钢筋缠绕钢筒混凝土压力管(BCCP)承受内、外压能力有限元分析
2019-11-04孙岳阳胡少伟黄逸群
孙岳阳,胡少伟,王 洋,黄逸群,薛 翔
(1.南京水利科学研究院,江苏 南京 210024; 2.河海大学,江苏 南京 210024)
钢筋缠绕钢筒混凝土压力管(Bar-wrapped Cylinder Concrete Pressure Pipe,BCCP)的结构型式和传统的预应力钢筒混凝土管(Prestressed Concrete Cylinder Pipe,PCCP)类似,根据钢筒位置分为内衬式(BCCP-L)和埋置式(BCCP-E)。内衬式(BCCP-L),在钢筒内部浇筑混凝土形成管芯,钢筒外缠绕预应力钢筋,再浇筑细石混凝土保护层,结构型式如图1(a)所示;埋置式(BCCP-E),将钢筒埋置于混凝土内跟混凝土一起形成管芯,然后在管芯外缠绕预应力钢筋,再浇筑细石混凝土保护层,结构型式如图1(b)所示。与PCCP相比,BCCP有以下两个特点:(1)使用较粗的冷轧带肋预应力钢筋,钢筋应力等级低,克服了高应力造成的钢筋应力脆化问题;(2)在带肋钢筋上浇筑细石混凝土保护层,具有更密实、高强、抗拉、防腐的优越性能。

图1 BCCP结构示意图
国内外对PCCP受力性能的研究很多,在上个世纪,Rose[1]、Zarghamee[2]和Tremblay[3]等国外学者对PCCP进行试验研究,揭示了PCCP的承载机理。引进我国后,胡少伟等[4-6]、窦铁生等[7-9]学者通过原型试验与数值仿真对PCCP在不同荷载作用下的承载能力和破坏机理进行了研究,取得了很大的进展。BCCP是基于PCCP而改进的新产品,自诞生到应用还不到五年,相关研究较少。胡少伟等[10-12]建立了BCCP的缠筋模型、研究了预应力损失对其受力性能的影响以及地基沉降对接口力学性能的影响。BCCP在预应力钢筋和保护层上与PCCP有明显的不同,其内、外压承载能力研究较少,而现场原型试验研究耗费巨大。为此,本文通过有限元软件ABAQUS建立BCCP承受内、外压的计算模型,获得承载过程中各部位进入塑性时的内、外压大小,对BCCP的应用推广具有十分重要的意义。
1 BCCP有限元模型
1.1 几何尺寸与材料参数
BCCP模型的几何尺寸和材料参数参考宁夏青龙管业股份有限公司生产的成品管,共选择两种管径:DN1400和DN1800,结构型式都是埋置式(BCCP-E)。
各管径几何尺寸及材料力学参数见表1和表2[13],管芯和保护层均采用C50混凝土浇筑。

表1 BCCP几何尺寸

表2 BCCP材料力学参数
1.2 模型建立
根据BCCP受力特点,在结果满足分析的基础上,提高模型计算效率,建立BCCP有限元模型时作如下简化假设:(1)考虑材料的非线性,不考虑几何非线性;(2)小变形假设;(3)不考虑各材料之间的粘结滑移效应,管芯混凝土与钢筒采用共用节点的方式协调工作;(4)假设预应力钢筋与管芯及保护层之间位移连续,采用绑定约束模拟预应力钢筋与管芯、预应力钢筋与保护层之间的相互作用;(5)不考虑混凝土材料的干缩、徐变等效应对管体结构受力的影响。

图2 有限元模型
1.3 材料本构
(1) 混凝土本构模型。采用ABAQUS软件中提供的塑性损伤模型作为混凝土的本构模型[15],该模型考虑了混凝土拉压性能的差异,最终破坏方式有受压破碎和受拉开裂两种。
(2) 预应力钢筋本构模型。预应力钢筋的本构模型采用如下应力应变关系:
fs=εsEsεs
(1)
式中:fsu为预应力钢筋抗拉强度;fsg为预应力钢筋的张拉应力;预应力钢筋屈服应力为其抗拉强度的85%,fsy=0.85fsu;图3为预应力钢筋应力应变曲线。
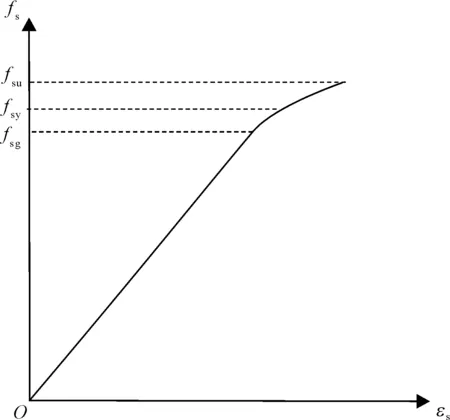
图3 预应力钢筋应力应变关系曲线
(3) 钢筒本构模型。根据AWWA C304中的建议[16],钢筒采用理想的弹塑性应力应变关系,关系曲线如图4所示。
1.4 钢筋预应力的模拟
本文采用等效降温法给钢筋施加预应力[17],利用物体热胀冷缩的属性,对模拟预应力钢筋的“梁”单元实施降温,使梁产生收缩,从而对钢筒和管芯产生预压应力,降温值按式(2)进行计算。
(2)
式中:Δt为需施加的降温值;α为预应力钢丝线膨胀系数,本文取0.000 1。

图4 钢筒应力应变关系曲线
2 计算结果
2.1 内压计算结果
(1) 缠筋后计算结果。内压管计算模型管径为1 400 mm,缠筋后,管芯混凝土和钢筒受到张拉预应力钢筋所产生的预压应力,此时最外层的混凝土保护层不参与受力,计算时采用ABAQUS中的生死单元法,将砂浆保护层单元杀死,各部位应力计算结果如图5所示,图中数值单位为MPa,受拉为正,受压为负(下同)。各部位端部受边界条件的影响与管身部位的计算结果差别较大,只取管身应力进行分析。管芯最大受压应力为13.03 MPa,钢筒最大受压应力为74.85 MPa,钢筋受拉应力最小为407 MPa。根据表2中预应力钢筋的张拉应力为72%fsu,即468 MPa,缠筋后钢筒和混凝土产生弹性压缩变形,钢筋受拉应力减小,所以模型计算结果比钢筋张拉应力要小,符合实际情况。在此阶段,各部分均处于弹性状态,无损伤,充分发挥了混凝土抗压能力强、钢筋抗拉性能好的材料优势。
(2) 混凝土保护层进入塑性。当内压加大至1.1 MPa时,混凝土保护层开始进入塑性,塑性应变云图如图6(a)所示,图中数值单位为ε。此时,管芯混凝土、钢筒和钢筋的应力计算结果云图见图6(b)—图6(d)。从图中可以看出钢筒内管芯混凝土基本还处于受压状态,钢筒外管芯逐渐由受压转变为受拉,受拉应力还较小,在2MPa以下,并未达到极限抗拉强度。此时钢筒的应力为50 MPa左右,为受压应力,钢筋拉应力在435 MPa左右,整管还能继续承受更大的内压。
合作学习法是通过分组的教学模式,让学生在课堂上相互帮助、彼此协作,实现优势互补,促进自己和同伴的共同学习与进步,达到课堂学习效果最大化的目的,因此合作学习可以互帮互助,达到共同进步的目的,实验后足球技能数据如表4所示:
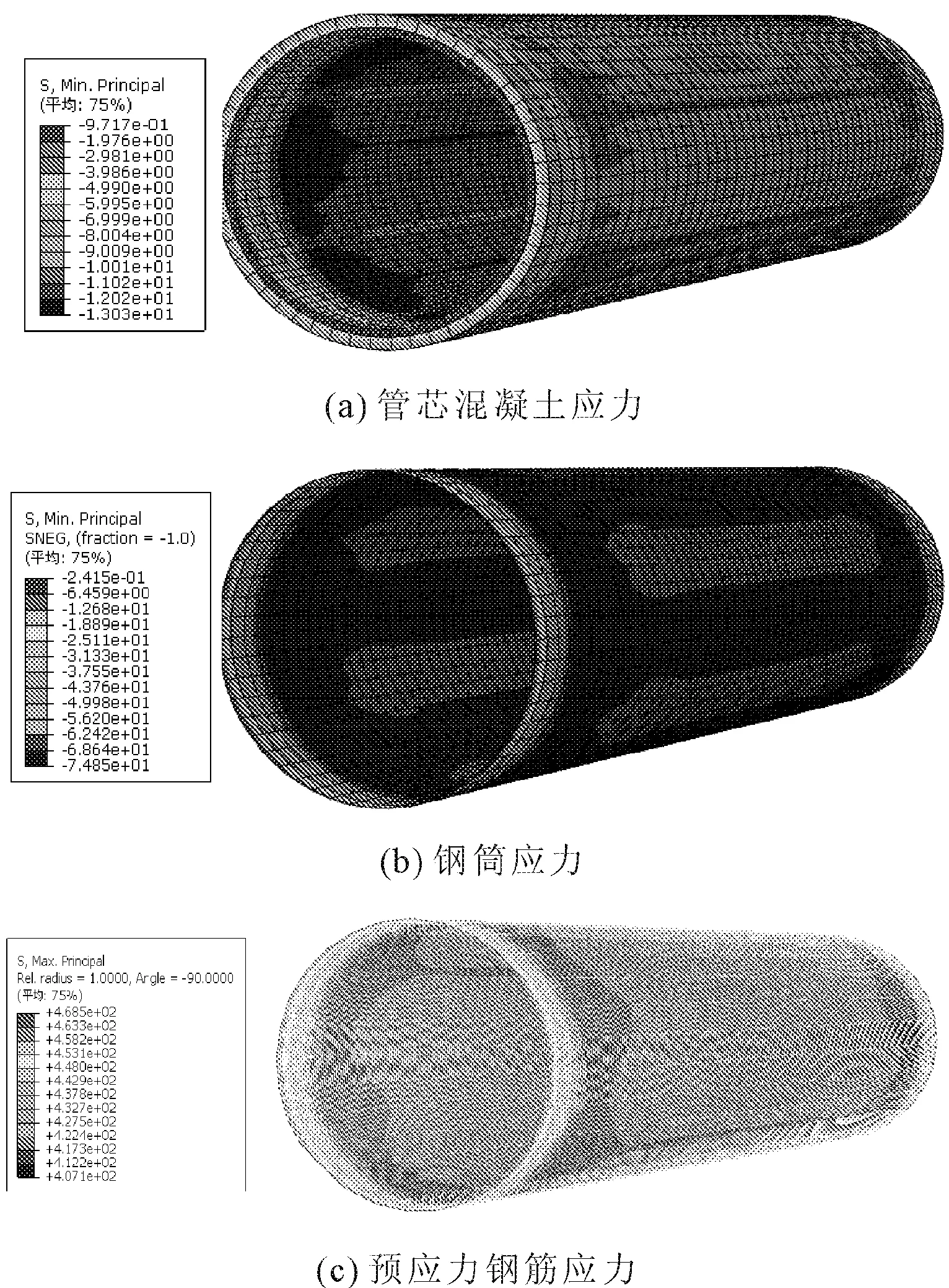
图5 缠筋后各部位计算结果云图
(3) 管芯混凝土进入塑性。内压继续加大至1.5 MPa时,钢筒外管芯混凝土开始进入塑性,塑性应变云图如图7(a)所示。此时混凝土保护层已完全进入塑性,塑性应变云图如图7(b)所示,可以认为完全退出工作,钢筒和钢筋的应力分布见图7(c)和图7(d)。从图中可以看出,钢筒的应力为25 MPa左右,依然为受压应力,钢筋拉应力在450 MPa左右,均未达到屈服强度。
(4) 管芯混凝土完全进入塑性。当内压升至3.2 MPa时,钢筒内管芯混凝土内表面出现塑性应变,即表示整个管芯完全进入塑性,塑性应变云图如图8(a)所示,此后的加载可认为管身混凝土完全退出工作。此时钢筒和钢筋的应力分布见图8(b)和图8(c)。钢筒的应力为35 MPa左右,由初始的受压应力转变为受拉应力,钢筋拉应力在495 MPa左右,小于其屈服强度。

图6 混凝土保护层进入塑性后各部位计算结果云图

图7 管芯混凝土开始进入塑性时各部位计算结果云图

图8 管芯混凝土完全进入塑性时各部位计算结果云图
(5) 钢筒屈服。最终当内压加大至6.8 MPa时,钢筒基本达到屈服强度235 MPa,应力云图如图9(a)所示。钢筋最大拉应力为646 MPa,应力云图如图9(b)所示,接近抗拉强度650 MPa,内压已不能再继续增加,钢筒和预应力钢筋几乎同时达到各自的极限强度,说明BCCP管型选材以及尺寸设计的合理。

图9 钢筒屈服时各部位计算结果云图
2.2 外压计算结果
(1) 缠筋后计算结果。外压管计算模型管径为1 800 mm,缠筋后各部位的受力情况与内压管计算结果不同,如图10所示。同样取管身应力进行分析,管芯最大受压应力为12.76 MPa,钢筒最大受压应力为73.20 MPa,钢筋最小受拉应力为411 MPa,各部分均处于弹性状态。

图10 缠筋后各部位计算结果云图
(2) 混凝土保护层进入塑性。当外压加载至900 kN时,管腰混凝土保护层开始进入塑性,塑性应变云图如图11(a)所示;此时管芯混凝土仍处于弹性状态,应力云图如图11(b)所示,管腰处管芯受压应力最大,最大压应力为17.42 MPa;钢筒应力云图如图11(c)所示,全部受压,最大受压应力在管腰处,为89.62 MPa;钢筋应力云图如图11(d)所示,管腰处拉应力较管顶和管底大,最大拉应力在425 MPa左右。
(3) 钢筒内管芯混凝土进入塑性。外压加载至1 500 kN时,钢筒内管芯顶部混凝土从端部开始进入塑性,其余大部分仍处于弹性工作状态,应力云图如图12(a)所示,管腰处内管芯受压应力最大,最大压应力为18.19 MPa;此时混凝土保护层大范围进入塑性,后续加载可认为其完全退出工作,钢筒应力云图如图12(b)所示,依然全部受压,最大受压应力在管腰处,为91.98 MPa;钢筋应力云图如图12(c)所示,管腰处拉应力较管顶和管底大,最大在440 MPa左右。

图11 混凝土保护层进入塑性后各部位计算结果云图
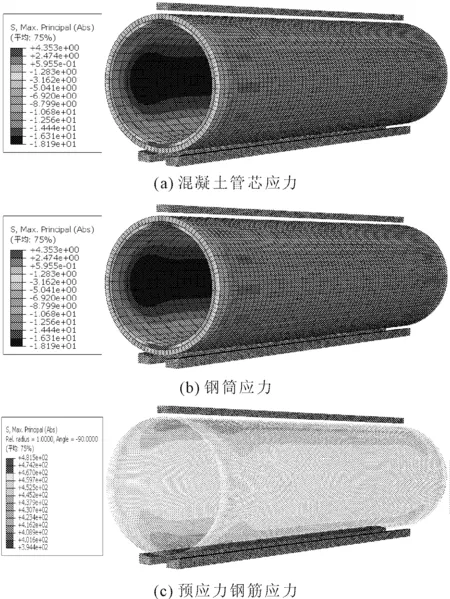
图12 钢筒内管芯混凝土进入塑性时各部位计算结果云图
(4) 钢筒外管芯混凝土进入塑性。最终外压加载至2 175 kN时,钢筒外管芯腰部混凝土开始进入塑性,钢筒内管芯混凝土顶部与底部大面积进入塑性,应力云图如图13(a)所示,管腰处内管芯受压应力最大,最大压应力为23.41 MPa;钢筒应力云图如图13(b)所示,依然全部受压,最大受压应力在管腰处,为106.60 MPa;钢筋应力云图如图13(c)所示,管腰处拉应力较管顶和管底大,最大在450 MPa左右。
由文献[18]可知,预应力钢筒混凝土管外压加载至管芯混凝土顶部和腰部相继进入塑性后整管会很快丧失承载力,故本文计算BCCP承受外压的能力时模拟到钢筒外管芯混凝土开始进入塑性阶段。

图13 钢筒外管芯混凝土进入塑性时各部位计算结果云图
2.3 结果汇总分析
DN1400 BCCP承受内压过程中,由于缠绕预应力钢筋,初始状态下管芯混凝土和钢筒受压,管芯最大受压应力为13.03 MPa,钢筒最大受压应力为74.85 MPa;当内压小于1.10 MPa时,各部位应力均小于其设计强度,处于弹性状态;内压继续增大,保护层开始进入塑性,到1.5 MPa时管芯混凝土也开始进入塑性;内压3.2 MPa时,管芯混凝土完全进入塑性,钢筒和钢筋应力迅速增加;最终加载至6.8 MPa,钢筒和钢筋均达到其抗拉强度,整管丧失承载力。
DN1800 BCCP承受外压过程中,同样因为预应力的作用,初始状态下管芯混凝土和钢筒受压,管芯最大受压应力为12.76 MPa,钢筒最大受压应力为73.20 MPa;当外压小于900 kN时,各部位均处于弹性状态。随后,管腰部位混凝土保护层达到其抗拉强度,开始进入塑性;外压1 500 kN时,管芯顶部从管端部开始进入塑性;最终加压到2 175 kN,钢筒外管芯腰部混凝土受拉进入塑性,整管很快丧失承载力。
PCCP设计时采用极限状态设计法[16,19],以三种极限状态作为设计准则,分别为工作极限状态、弹性极限状态和强度极限状态。通过计算不同工况下各部位的应力应变分布,逐一验证是否满足各极限状态设计准则的要求。工作极限状态设计准则,指管道在正常运行条件下,管芯混凝土和外层砂浆保护层不出现微裂缝和可见裂缝;弹性极限状态准则,指管道在荷载作用下欲开裂时,具备足够的弹性避免发生破坏或预应力损失;强度极限状态,指管道达到其最大承载力时,管芯不发生开裂以及预应力钢丝不发生屈服断裂。实际管道运行时,不仅仅承受内压、外压以及自重,还有土荷载以及路面活荷载和流体自重。为此,本文以保护层开始进入塑性作为达到工作极限状态,管芯混凝土开始进入塑性作为达到弹性极限状态,钢筒内、外管芯混凝土均进入塑性作为进入强度极限状态,则根据2.1节、2.2节中有限元模拟计算的结果,本文建立的BCCP模型各极限状态对应的内、外压值见表3。

表3 各极限状态对应的内、外压值
由表3数据可知,内压管弹性极限状态对应的内压值比工作极限状态对应的高0.4 MPa,而强度极限状态对应的内压值比弹性极限状态对应的高出1.7 MPa。分析可知,承受内水压过程中管芯混凝土环向应力会达到其抗拉强度而产生径向裂缝,但由于钢筒以及环向预应力钢筋对混凝土的包裹,开裂的混凝土依然可以在径向传递压力,并没有完全退出工作,所以强度极限状态对应的内压值较大。而外压管弹性极限状态与工作极限状态对应外压的差值和强度极限状态与弹性极限状态对应的差值基本一致,分别为600 kN和675 kN,原因是承受外压过程中混凝土进入塑性后则很快退出工作,对后期继续承载基本没有贡献,管顶和管底部位的混凝土是由内向外,钢筒内管芯先进入塑性;管腰部位的混凝土则是由外向内,外保护层先进入塑性,所以弹性以及强度极限状态与前一极限状态对应的外压差值基本一致。
3 结 论
DN1400 BCCP承受内压过程中,当内压达到1.1 MPa时,保护层开始进入塑性,管芯、钢筒和预应力钢筋依旧处于弹性状态;1.5 MPa时管芯混凝土也开始进入塑性;到3.2 MPa时,管芯完全进入塑性;最终加载至6.8 MPa,钢筒和钢筋均达到其抗拉强度,整管丧失承载力。DN1800 BCCP承受外压过程中,当外压达到900 kN时,管腰部位混凝土保护层达到其抗拉强度,开始进入塑性; 1 500 kN时,管芯顶部从管端部开始进入塑性;最终加压到2 175 kN,钢筒外管芯腰部混凝土受拉进入塑性,整管很快丧失承载力。
外压管弹性以及强度极限状态与前一极限状态对应的外压差值基本一致,相差不大,分别为600 kN和675 kN,而内压管强度极限状态与弹性极限状态所对应的内压差值达1.7 MPa,说明混凝土破坏后,钢筒和预应力钢筋应力远小于各自的设计强度,有较大富余,给了BCCP较高的安全保障。
