内部爆炸作用下钢筒变形过程的电探针测量技术*
2014-12-12秦学军张德志史国凯刘峻岭
秦学军,张德志,杨 军,史国凯,刘峻岭,王 惠,熊 琛
(西北核技术研究所,陕西 西安710024)
对内部爆炸作用下钢筒的变形,已有了许多研究。T.Duffy等[1]对弹塑性钢环和长圆柱壳体的应变硬化和应变率敏感性进行了研究。N.Rushton等[2]对内部爆炸作用下壁厚9.5mm、长度800mm、外径324mm的钢筒进行实验和数值模拟研究,证明相同爆炸当量的圆柱形炸药比球形炸药使钢筒爆心截面处的变形量大。T.Duffy等[3]假定实验材料为理想刚塑性体,在爆炸过程中钢筒沿轴向没有变形,实验材料对应变硬化和应变率效应不敏感,对爆心截面处钢筒的径向位移进行了研究。钟方平等[4]对球形和柱形装药爆炸作用下的多层圆柱形钢筒的塑性变形进行了研究。钢筒受爆炸冲击后的径向变形测量,对于爆炸力学参数的分析和研究具有重要的意义。
目前,测量内部爆炸作用下金属圆筒变形主要手段有:在金属圆筒外壁粘贴应变计对容器的动态变形进行测量[5];实验后直接测量金属圆筒的变形量;利用高速相机对爆炸载荷下金属圆筒的变形进行连续拍照[6],进行数据处理,得到金属圆筒的变形情况;此外,还有利用激光的多普勒效应测量爆炸容器的径向变形[7]。应变片测量变形不大于0.02,且在测量中径向变形参数需要进一步推导和换算;实验后直接测量容器变形量,由于工具和人为因素对测量结果造成一定的误差,也无法反映金属圆筒变形与时间的关系;金属圆筒变形高速摄影实验需要时间和空间分辨率很高的高速相机及光源等配套设备,一般实验室不具备实验条件。
本文中,采用电探针测量技术结合数值模拟方法预估,对120g TNT和180g TNT当量装药爆炸作用下、20钢筒(两端开口)爆心截面处外壁环向不同位置的变形量进行分时测量,以得到爆心截面处钢筒的变形过程。
1 电探针测量技术
1.1 数值模拟预估
运用数值模拟方法可以预估爆炸作用下钢筒的变形,根据预估钢筒的变形结果,可以对电探针距离钢筒外壁的位置进行设计。利用数值模拟方法,对120g TNT和180g TNT当量装药爆炸作用下长度600mm、壁厚12mm、外径124mm的20钢筒的动力学响应进行预估。
模拟中,空气、炸药采用欧拉网格,钢筒采用拉格朗日网格,钢筒和空气、炸药之间采用Euler/Lagrange耦合算法,欧拉区域两端边界条件设为外流模式,拉格朗日区域两端为自由边界。
空气采用理想气体模型;炸药采用JWL爆轰产物状态方程;20钢采用John-Cook强度模型和状态方程。
图1为模拟计算模型,假设在爆炸作用下爆心截面处钢筒外壁各处的变形情况相同,取爆心截面处钢筒外壁一个特征点进行分析。图2为120和180g TNT当量装药爆炸下爆心截面处的钢筒外壁环向应变曲线。
数值模拟得到:120g TNT当量爆炸时,爆心截面处钢筒外壁的最大径向变形为约4.2%,对应的半径增量为约2.60mm;180g TNT当量时,最大径向变形为约8.6%,半径增量为约5.33mm。可以根据数值模拟的结果,对电探针在钢筒外壁周向布放进行设计。
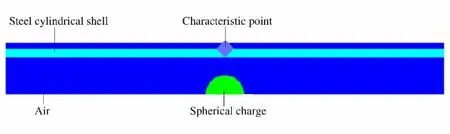
图1 计算模型示意图Fig.1 Schematic diagram of calculation model
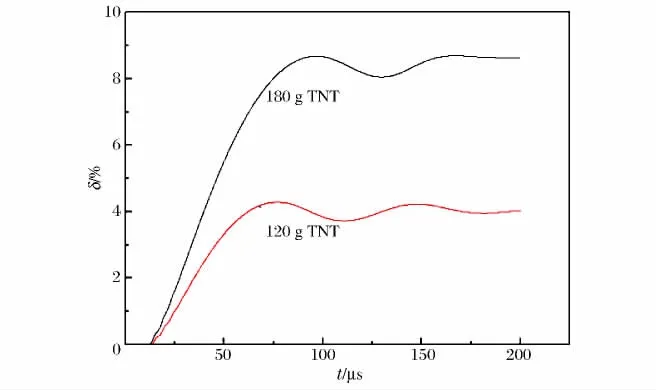
图2 爆心截面处钢筒外壁环向应变Fig.2 Ektexine’s loop deformation of cylindrical steel shell under center explosion
1.2 钢筒变形
电探针测量内部爆炸作用下金属圆筒变形的方法是,在爆心截面处金属圆筒外壁周围不同位置处利用定位环安放电探针,电探针的数量根据实验的需要可以在定位环上进行安置。根据数值模拟估算内部爆炸作用下钢筒的变形量,在爆心处钢筒外的定位环上安放电探针,电探针与金属圆筒外壁间的距离通过塞尺测量定位。球形炸药引爆后,定位环上不同位置处的电探针与金属圆筒接触产生脉冲信号,获得金属圆筒径向位移与电探针接触金属圆筒的时间,也就得到了金属圆筒在不同时刻的变形量。
图3为电探针测量钢筒变形示意图。钢筒的外径124mm、壁厚12mm、长度600mm。实验前在钢筒外对定位环位置进行固定,通过定位环利用塞尺测量各探针与钢筒外壁间的间距,使不同位置探针与钢筒之间的距离固定。图4为电探针测量系统示意图。
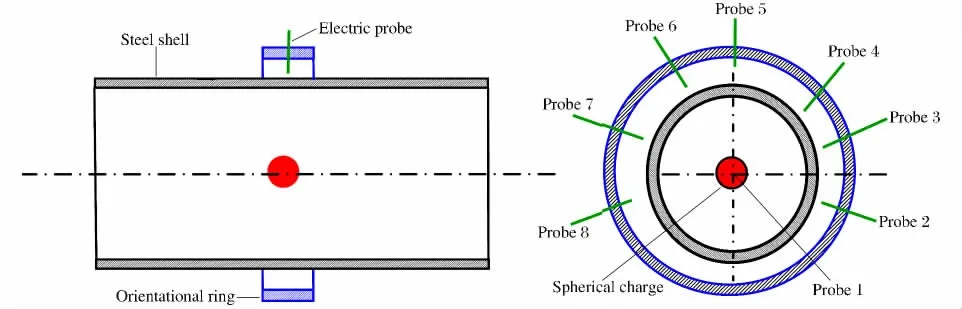
图3 电探针位置示意图Fig.3 Schematic diagram of the location of electric probes

图4 电探针测量系统示意图Fig.4 Schematic diagram of electric probes measurement system
2 实验结果及分析
在20钢筒内部进行120g TNT和180g TNT当量的爆炸实验。
在120g TNT和180g TNT当量的爆炸实验中,分别设置8路探针:在爆心处设置电探针1,在定位环-18°、18°、54°、90°、126°、162°和198°等7个位置处设置电探针2~8,电探针距离钢筒外壁面的距离l见表1~2,实验结果如图5所示。其中,ts为探针触发时刻,δ为变形量。
以炸药爆炸的时间为基准,可得到电探针2~8接触壁面的准确时间,即得到了钢筒在不同时刻的变形量,表1~2为120g TNT、180g TNT当量爆炸实验电探针测量结果。
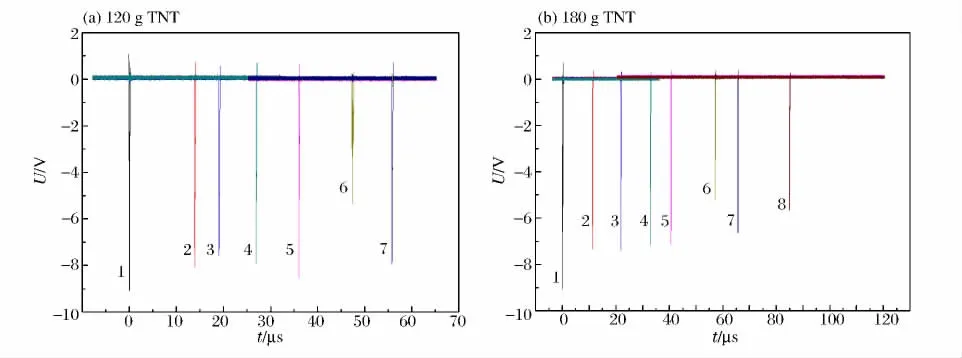
图5 电探针测量的脉冲波形Fig.5 Waveform of electric probes measurement
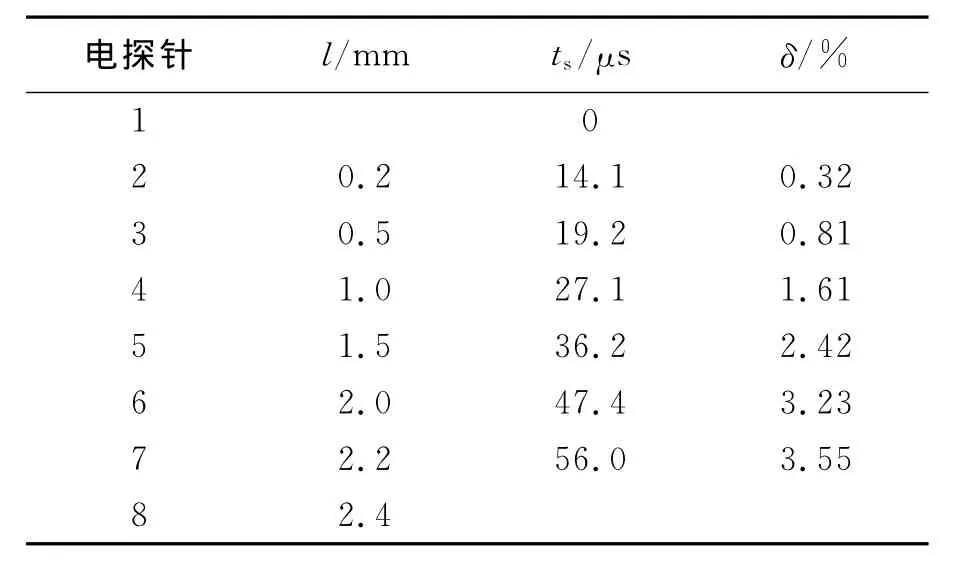
表1 120g TNT当量爆炸实验电探针测量结果Table 1 Experimental result of electric probes measurement under 120g TNT charge
通过电探针距离钢筒壁面的距离和电探针与钢筒的接触时间,可以得到钢筒外壁径向位移与时间的关系,如图6(a)所示。对于120g TNT和180gTNT当量的爆炸实验,同样距离钢筒外壁2.0mm的电探针,180g TNT当量爆炸电探针与钢筒接触用时比120g TNT当量爆炸短,说明180g TNT当量爆炸时钢筒外壁的运动速度更快。通过对实验拟合曲线进行微分,可以估算钢筒外壁的运动速度,见图6(b)所示。120g TNT当量实验钢筒外壁的最大运动速度为约73m/s,180gTNT当量实验钢筒外壁的最大运动速度为约110m/s。

图6 钢筒外壁位移和速度Fig.6 Ektexine’s displacements and velocities
将实验得到的钢筒外壁位移和时间关系与数值模拟得到的结果进行比较,如图7所示。两者的趋势比较一致,从炸药开始爆炸到钢筒变形结束,持续的时间在100μs以内。

图7 钢筒外壁位移的实验结果和数值模拟结果Fig.7 Experimental and simulational results of ektexine’s displacement
实验后对钢筒的变形进行测量,120g TNT实验爆心截面处钢筒外壁的最大变形量为3.68%,钢筒外壁的径向位移为2.28mm;180g TNT 爆炸实验爆心截面处钢筒外壁的最大变形量为8.30%,钢筒外壁的径向位移为5.15mm。对电探针测量的爆心截面处钢筒外壁最大径向位移曲线求最大值,在120g TNT实验,爆心截面处钢筒外壁的最大径向位移约2.33mm,与实验后测量得到爆心截面处钢筒最大径向位移的相对误差为2.2%;在180g TNT实验,爆心截面处钢筒外壁的最大径向位移约5.43mm,与实验后测量得到爆心截面处钢筒最大径向位移的相对误差为5.8%。实验后爆心处钢筒最大变形量与电探针测量的结果比较一致,证明电探针测量钢筒变形方法是可行的。
3 结 论
电探针测量内部爆炸作用下钢筒变形,可以获得不同时刻钢筒的径向位移随时间的变化关系,获得钢筒在不同时刻的变形量。电探针测量钢筒变形的方法具有原理简单、测量变形范围大、容易操作等优点,尤其适用于钢筒的大变形测量。
[1]Duffey T,Krieg R.The effects of strain-hardening and strain-rate sensitivity on the transient response of elasticplastic rings and cylinders[J].International Journal of Mechanical Sciences,1969,11(10):825-844.
[2]Rushton N,Schleyer G K,Clayton A M,et al.Internal explosive loading of steel pipes[J].Thin-Walled Structure,2008,46(7/8/9):870-877.
[3]Duffey T,Mitchell D.Containment of explosions in cylindrical shell[J].International Journal of Mechanical Sciences,1973,15(3):237-249.
[4]钟方平,马艳军,张德志,等.多层圆柱壳钢筒在球形和柱形装药爆炸作用下塑性变形的研究[J].兵工学报,2009,30(2):194-196.Zhong Fang-ping,Ma Yan-jun,Zhang De-zhi,et al.Research on plastic deformation of multi-layer cylindrical steel tube subjected to blasts of spherical and cylindrical charges[J].Acta Armamentarii,2009,30(2):194-196.
[5]钟方平,陈春毅,林俊德,等.带平板封头的双层爆炸容器动力响应的实验研究[J].爆炸与冲击,1999,19(3):199-203.Zhong Fang-ping,Chen Chun-yi,Lin Jun-de,et al.Experimental study of dynamic response of double-walled explosion vessels with flat head[J].Explosion and Shock Waves,1999,19(3):199-203.
[6]汤铁钢,谷岩,李庆忠,等.爆轰加载下金属柱壳膨胀破裂过程研究[J].爆炸与冲击,2003,23(6):529-533.Tang Tie-gang,Gu Yan,Li Qing-zhong,et al.Expanding fracture of steel cylinder shell by detonation driving[J].Explosion and Shock Waves,2003,23(6):529-533.
[7]胡永乐,陈子辰,王文,等.爆炸容器动态径向变形非接触测量技术[J].机械强度,2009,31(5):759-763.Hu Yong-le,Chen Zi-chen,Wang Wen,et al.Non-contact measurement technique for dynamic radial deformation of explosion containment vessels[J].Journal of Mechanical Strength,2009,31(5):759-763.
