一种复材层合板低速冲击后压缩强度估算方法

盛鸣剑，陈普会，钱一彬

(1.南京航空航天大学 航空宇航学院，南京 210016；2.中国商用飞机有限责任公司，上海 200126)

复合材料具有质量轻、强度高、可设计性好、成本低以及耐蚀耐候等优点，已在航空航天等领域得到了广泛应用[1-8].复合材料层合板是由2层或2层以上单层交错的材料粘合组成的结构板，每个单层又由平面铺设的增强体纤维和基体材料构成.研究表明[9-12]，复合材料层合板受到低速冲击后，其性能尤其剩余压缩强度会急剧下降，这在很大程度上会削弱构件的承载能力，并破坏材料结构的完整性[7,13].因此，研究低速冲击后复合材料层合板损伤程度对剩余压缩强度的影响以及剩余压缩强度的估算方法对复合材料结构设计具有重要的意义.

复合材料层合板低速冲击后压缩强度的研究方法主要有4种.① 损伤演化法：利用动态有限元计算层合板的冲击损伤，以其对应的退化后刚度作为层合板的初始损伤，再用损伤演化模拟层合板的压缩破坏过程并计算剩余压缩强度[14-15]；② 软化夹杂法：将低速冲击后损伤视为规则形状的夹杂软化,再运用各种失效判据确定层合板的失效强度[16]；③ 子层屈曲法：将低速冲击后损伤看作多个面积不同、形状规则的分层,假设压缩破坏过程是各分层不断产生屈曲失效的过程,并认为所有分层屈曲破坏时材料结构发生破坏，以确定失效强度[3]；④ 开孔等效法：使用圆孔或椭圆孔等效替代低速冲击后损伤,再使用材料断裂韧性的判据来确定层合板破坏时的强度，作为失效强度[17].

本文分析不同能量等级的低速冲击后CCF300/5428材料体系的复合材料层合板压缩强度数据，提出一种基于广义回归神经网络技术的低速冲击后复合材料层合板压缩强度的新型预测方法.考虑到样本试验数据的特殊性及样本容量的局限性，对影响复合材料层合板低速冲击后压缩强度的材料体系力学属性、铺层顺序、铺层数量、增韧技术、几何尺寸、冲头形状、冲击能量、环境等因素进行简化.在此基础上，利用广义回归神经网络建立估算模型，运用试验数据训练并结合轮询遍历交叉检验法计算出高斯函数的最佳光滑因子.重构了神经网络估算模型并进行层合板压缩强度估算验证.经过对比分析模型估算数据与试验数据，认为估算结果较为准确、可靠，且估算过程快速而简单.

1 试验

复合材料层合板低速冲击试验及冲击后压缩强度试验采用的材料体系为CCF300/5428.试件的典型铺层为40层，铺层角顺序为[45/0/-45/90/0]4S，其中45，90以及0表示铺层方向分别为45°，90°以及0°，4为重复次数，S为对称之义.单铺层的名义厚度为 0.2 mm.单层材料的力学性能见表1.E1为纵向弹性模量，E1=148.8 GPa；E2为横向弹性模量，E2=10.02 GPa；G12为剪切模量；υ12为泊松比，υ12=0.31；Xc为纵向压缩强度，Xc=1.44 GPa.

按照ASTM D7136落锤冲击试验标准进行复合材料层合板低速冲击试验.试件尺寸为100 mm×150 mm×8 mm，试验区域的尺寸为75 mm×125 mm×8 mm.试验环境条件为干态室温，试验组数为24，冲头选用直径为 12.7 mm的半球形冲头.冲击能量(E)、冲击试验后试件表面凹痕深度(D)、冲击损伤面积(S)以及根据ASTM D7137标准测得试件冲击后剩余压缩强度(pc)数据见表1.

表1 冲击试验数据Tab.1 Data of the impact test

2 估算模型

2.1 广义回归神经网络

人工神经网络起源于对神经细胞行为模式在信息处理方面的研究，是智能学科的重要组成部分，为解决复杂问题和智能控制提供了有效的途径.虽然误差反传(Back Propagation,BP)神经网络算法回避了输入相关性问题，但是由于其具有的拓扑结构，估算模型容易陷入局部极小值的困境.另外，隐含层神经元个数依赖于经验公式，因此BP算法对经验与技巧的要求较高.径向基函数(Radical Basis Function,RBF)神经网络解决了局部极小值的问题，但其学习方法采用风险最小化原则，存在一定的经验成分，因此可能出现过学习问题.广义回归神经网络(General Regression Neural Network,GRNN)来源于RBF神经网络的变形，一般由输入层、隐含层、加和层及输出层等4层神经元构成，具有结构简单、收敛速度快、函数逼近能力强等特点.

GRNN优秀的泛化能力使其成为一种常用的模型工具，已广泛应用于各领域的预测与估算.本文使用广义回归神经网络技术建立层合板低速冲击能量与冲击后凹痕深度、损伤面积以及低速冲击后剩余压缩强度的映射关系.

2.2 估算模型结构

复合材料层合板低速冲击后剩余压缩强度大小是众多影响因素综合作用的结果.考虑到样本数据信息量的局限性,选取主要影响因素如低速冲击的能量、冲击后凹痕深度与损伤面积作为输入参数，而将冲击后剩余压缩强度作为目标输出.研究表明[18]，对于非线性映射问题，含有4层结构的广义回归神经网络可以实现无限逼近，并且具有柔性的网络结构和较好的容错性，适于解决影响因素间存在高度非线性关系的实际问题.因此，冲击后剩余压缩强度估算模型以广义回归神经网络作为模型框架，其输入层、输出层、隐含层以及求和层等的神经元节点数比较容易确定.根据估算模型设定的输入和输出维数分别为3和1，可以确定输入和输出层神经元节点数为3和1，而隐含层的神经元节点数等于训练样本数，求和层神经元节点数一般为2.

2.3 模型的算法

广义回归神经网络是径向基神经网络的改型，其理论基础是非线性核回归分析.对于假定的随机变量x与y，概率密度函数为f(x,y)，已知x的观察值为X,则y相对于x的回归条件均值为

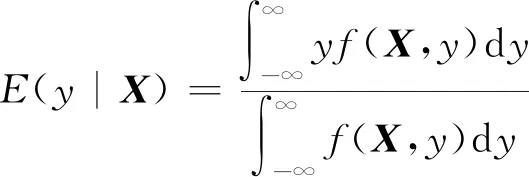
(1)

当f(x,y)未知时，y相对于x的回归分析实际上是计算具有最大概率值的y.通过对观测样本执行非参数估计，推导出观测样本中自变量和因变量的概率密度函数：

(2)

式中：p为输入变量的维度数；n为观测样本的容量数；σ为光滑因子(高斯函数宽度系数).

若观测样本的第k个样本为xk,隐含层的各个神经元对应一个期望输出yk.加和层的第1个神经元输出S1为隐含层输出yk乘以权值后的和，加和层的第2个神经元的输出S2为隐含层输出的直接求和，输出层的输出为S1/S2.与基于BP神经网络的估算模型相比，广义回归神经网络训练过程通常不需要迭代，且相关参数的确定较为简单，因此神经网络训练过程实际是确定光滑因子的过程.

σ对GRNN模型预测性能影响较大，σ取值过大可能使神经网络拟合偏差过大，而取值过小使得神经网络过学习.基础的广义回归神经网络隐含层一般采用同一个σ，样本数据的概率分布对GRNN模型为未知数，所以不能直接从样本中求得最佳光滑因子(σbest)，需使用观测样本对模型进行训练，搜寻求解σbest.搜寻过程一般使用轮询遍历交叉检验法和黄金分割快速搜寻法.

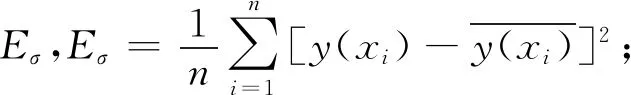
(2)黄金分割快速搜索法.假设σ1,σ2在σbest的搜索区间(a,b)内，σ1,σ2与a,b两点的距离相同且σ1<σ2，σ1,σ2计算方法为

(3)

3 模型验证

3.1 数据规范化处理

冲击后压缩强度与冲击能量、凹痕深度以及损伤面积与的关系如图1所示.可以看出，冲击后压缩强度与冲击能量和凹痕深度具有一定的线性关系，而与损伤面积之间不具备线性关系.

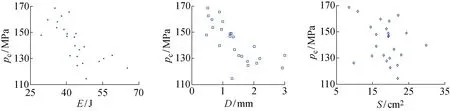
图1 冲击后压缩强度与冲击能量、凹痕深度以及损伤面积与的相关性Fig.1 Correlation between compressive strength after impact and energy,indentation depth,damage area

基于GRNN的低速冲击后压缩强度估算模型在使用通常单位的情况下，凹痕深度、冲击能量、损伤面积以及压缩强度数据的数量级分别为100、101、101以及102，量级差较大.为避免该情况对估算模型准确度的影响，将所有观测样本数据归一化转换为[-1,1]之间的数值.对GRNN模型得出的估算数值进行反向处理，将得出的数值反归一化转换至原值域.归一化与反归一化一般使用MATLAB中的PREMNMX、POSTMNMX、TRAMNMX等内置函数进行处理.归一化处理公式为

(4)

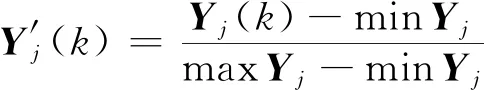
(5)

反归一化处理公式为

(6)

(7)

式中：i=1,2,3,分别为冲击能力、凹痕深度以及损伤面积；k为该维度中元素的坐标；j=1，为输出矩阵的维度.

3.2 参数优化

基于GRNN压缩强度估算模型建模使用的输入、输出参数以及所涉及调优参数较少，只需调整σ且为一维较小的搜索空间，轮询遍历交叉检验法与黄金分割快速搜索法计算量差别不大.因此，下文以均方根误差为目标函数，运用轮询遍历交叉检验法寻找最优光滑因子.

设定高斯函数光滑因子的寻优空间为σ∈[0.01,1]，步长Δ=0.000 5.从观测样本预处理后的数据中用函数随机抽取21组作为GRNN估算模型的训练调参数据，用于搜寻σbest.其余的3组作为验证数据，再将21组训练数据用函数随机分为3分组，每分组含7个数据点，分组依次编号.根据轮询遍历交叉检验法使用MATLAB环境进行编程计算，经过学习训练，得到模型训练过程中目标函数Eσ的最小值仅为 22.330 2 MPa.可见，GRNN估算模型经训练后Eσ较小且训练收敛性很好.可以认为，GRNN估算模型的Eσ已经能满足模型预测的误差要求，最小Eσ对应的σbest为0.415，用此值对基于GRNN的冲击后压缩强度估算模型进行重构，可用于下一步估算模型验证.

3.3 估算结果

GRNN模型重构后，将随机抽取的另外3组观测样本数据输入已完成训练的冲击后压缩强度估算模型进行模型仿真预测，得出估算数值后应用式(6)和(7)计算出模型估算的冲击后压缩强度，见表2.可以看出，模型仿真的3组验证数据的冲击后压缩强度估算值与试验值比较接近，绝对误差区间为[-6.395 7,7.146 8] MPa，相对误差区间为[-4.37%,5.11%].

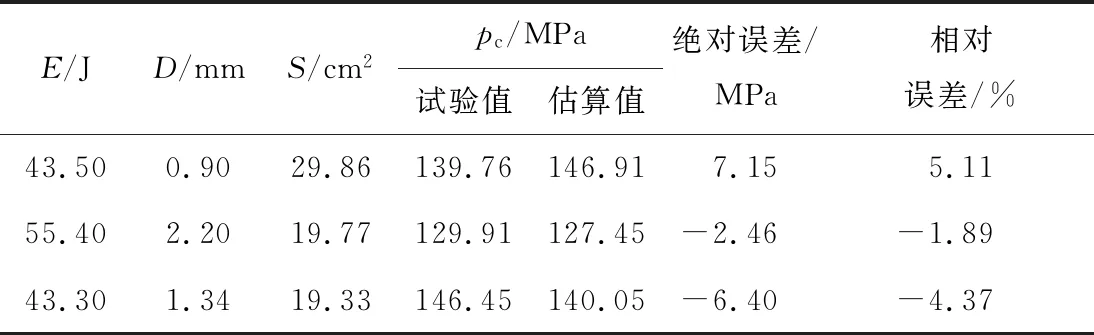
表2 GRNN模型估算的冲击后压缩强度Tab.2 Compression strength estimated by GRNN model after impact

由表2可知，使用基于GRNN神经网络的冲击后压缩强度估算模型得到的估算值与试验值能较好地吻合，但个别观测样本的估算数据与试验数据偏差超过5%.如在遭受冲击能量为 43.50 J的低速冲击后，测得凹痕深度为 0.90 mm、损伤面积为 29.86 cm2的情形下，测得压缩强度为 139.76 MPa，而模型估算得到的压缩强度为 146.91 MPa，误差为 7.1 MPa.误差产生的可能原因有：① 复合材料层合板低速冲击试验后，所测损伤面积与实际损伤面积存在一定的误差；② 冲击后产生的表面凹痕有明显回弹效应，测量间隔时间在一定程度上影响凹痕深度精度；③ 基于GRNN估算模型需一定数量的观测数据训练，样本容量较小可能导致精度较低.

4 结语

复合材料层合板遭受低速冲击后，其力学性能的下降程度与损伤严重程度密切相关，而凹痕深度和损伤面积是损伤程度的主要表征参数.本文应用广义回归神经网络，以冲击能量、凹痕深度和损伤面积作为输入参数建立了复合材料层合板受到低速冲击后压缩强度估算模型.使用部分试验样本数据对广义回归神经网络压缩强度估算模型训练后，选取另一部分样本数据进行仿真验证.结果表明：基于广义回归神经网络的压缩强度估算模型计算效率较高且估算结果较为准确，该模型为复合材料层合板低速冲击后压缩强度估算提供了一种有效的新方法.