不同施痕物下凹痕管道残余应力的有限元分析*

张 鹏，黄云飞，伍 颖

(西南石油大学 土木工程与建筑学院，四川 成都 610500)

0 引言

机械损伤是引发陆地油气管道失效的首要原因。机械损伤中最为常见的类型是凹痕[1-2]，凹痕是管壁塑性变形导致管道横截面发生总的变形[3]，在管道施工期间可能会造成凹痕缺陷，如在管段搬运及管沟回填过程中受到岩石等硬物的碰撞和挤压。这些外载荷均能使管道表面产生不同形状的凹痕，对管道安全运行产生威胁[4-5]。因此，有必要了解不同形状施痕物产生的凹痕对管道安全性影响。

从上个世纪70年代开始，学者就对管道进行实验来模拟凹痕缺陷。伍颖等[6]根据现场数据，采用有限元法对凹痕处最大应力进行分析，得到了最大应力的计算式，但是这种公式缺乏普遍适用性；马欣等[7]采用有限元软件对凹痕管道进行了研究，探讨了凹痕深度等参数的变化对管道轴向应变和韧性损伤因子的影响；黄超等[8]基于韧性断裂模型和损伤力学，建立管道凹痕损伤评估模型，并结合有限元法研究了平滑和曲折2种凹痕缺陷不同区域的损伤程度；Baek等[9]研究了含凹痕缺陷的管道在受内压和平面内弯矩作用下，凹痕尺寸对管道的破坏行为的影响，得出当凹痕深度达到管道外径的5%时，凹痕管道的荷载承载力和没有缺陷的管道相比并没有下降；Hyde等[10]分析了凹痕区域由于凹痕的回弹而产生的残余应力，分析了不同参数对残余应力的影响；Ramezani等[11]采用有限元方法分析压力管道受挤压形成的管道凹痕缺陷； Allouti等[12]采用球体施痕物对管道施加凹痕缺陷，对力学实验结果和有限元数值模拟结果进行对比，得出凹痕深度等于管道外径的10%的结果是十分保守的。

大多数论文对凹痕管道的研究都忽略了施痕物几何形状对管道的影响。因此，本文主要分析椭球体、圆柱体和矩形体施痕物产生的凹痕缺陷管道，移除施痕物，改变施痕物尺寸、凹痕深度、管道壁厚，分析凹痕处最大残余应力σmax的变化规律，并拟合出残余应力与各参数关系表达式。

1 有限元模型的建立

管材选X80钢材，管材特性参数见表1。

表1 X80管材特性参数Table 1 Tube characteristic parameters of X80

采用ANSYS中的SHELL181壳单元进行管道模型建立，因管道模型和荷载条件对称性，只建立1/4管道模型。为了避免管道端部结构影响凹痕的分析结果，管道模型长度取3倍管道直径[13]。在编号为1，2，3的截面上施加对称约束。根据管道的实际情况，在编号为4的截面上施加固结约束。假设地面对管道模型的约束是刚性且沿管道全长的，故对管道模型底端约束其Y向自由度，沿管环向约束范围为120°。1/4管道模型见图1，施痕物模型采用SOLID185实体单元进行建立，考虑到本文采用的是位移荷载，为了使得位移更加准确，选用刚体模型。在凹痕区域进行网格细化，远离凹痕区域采用疏松网格[14]。

图1 1/4管道模型Fig.1 1/4 pipe model diagram

采用静态分析的方法，有限元模型见图2。有限元建模步骤如下：1) 施痕物垂直(平行)于管轴按压管道，对管道施加凹痕缺陷；2) 移除施痕物，记录凹痕区域的残余应力，应力用von Mises等效应力表示。

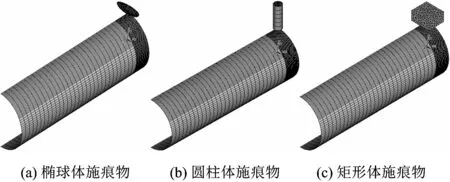
图2 管道有限元模型示意Fig.2 Schematic diagram of element model for pipeline

2 有限元模型的验证

为确保模型的可靠和合理，对R.Akbari Alashti等做的实验进行数值模拟，将结果与实验值作对比分析[15]。实验在1台60 t容量的万能力学实验机上完成，实验管道未充压。管道标本长度1 300 mm，管外径219 mm，壁厚4.8 mm。施痕物是刚性球形工具，直径75.3 mm。管材为API XB，弹性模量2×105MPa，泊松比0.3，屈服强度365 MPa，抗拉强度450 MPa。

实验结果与有限元结果对比见表2。从表中可知，轴向应变的相对误差都在5%以内，考虑实验边界条件，误差在允许范围内。因此，有限元结果与实验结果基本吻合，可以认为建立的有限元模型是合理的。

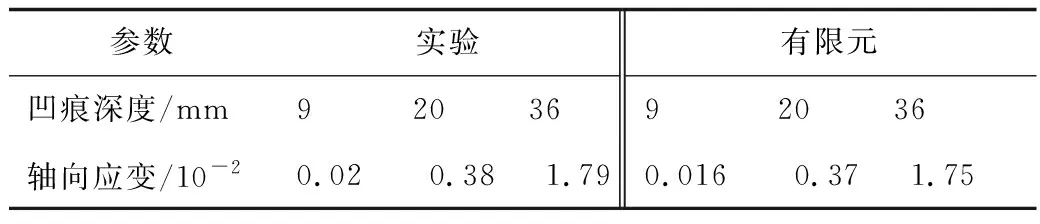
表2 实验结果与有限元结果对比Table 2 Comparison between results of test and FE

3 计算结果与分析

3.1 椭球体施痕物

3.1.1 椭球体长轴垂直于管轴

设管径D=1 000 mm；管道壁厚t，mm；椭球体短轴a，mm，长轴b=500 mm；凹痕深度d，mm。椭球体长轴垂直管轴施加凹痕。有限元计算结果见图3(以t/D=0.02，a/b=0.5，d/D=0.05时建立的模型为例)。计算算例与结果见表3。

图3 管道模型残余应力云图Fig.3 Cloud picture of pipeline residual stress

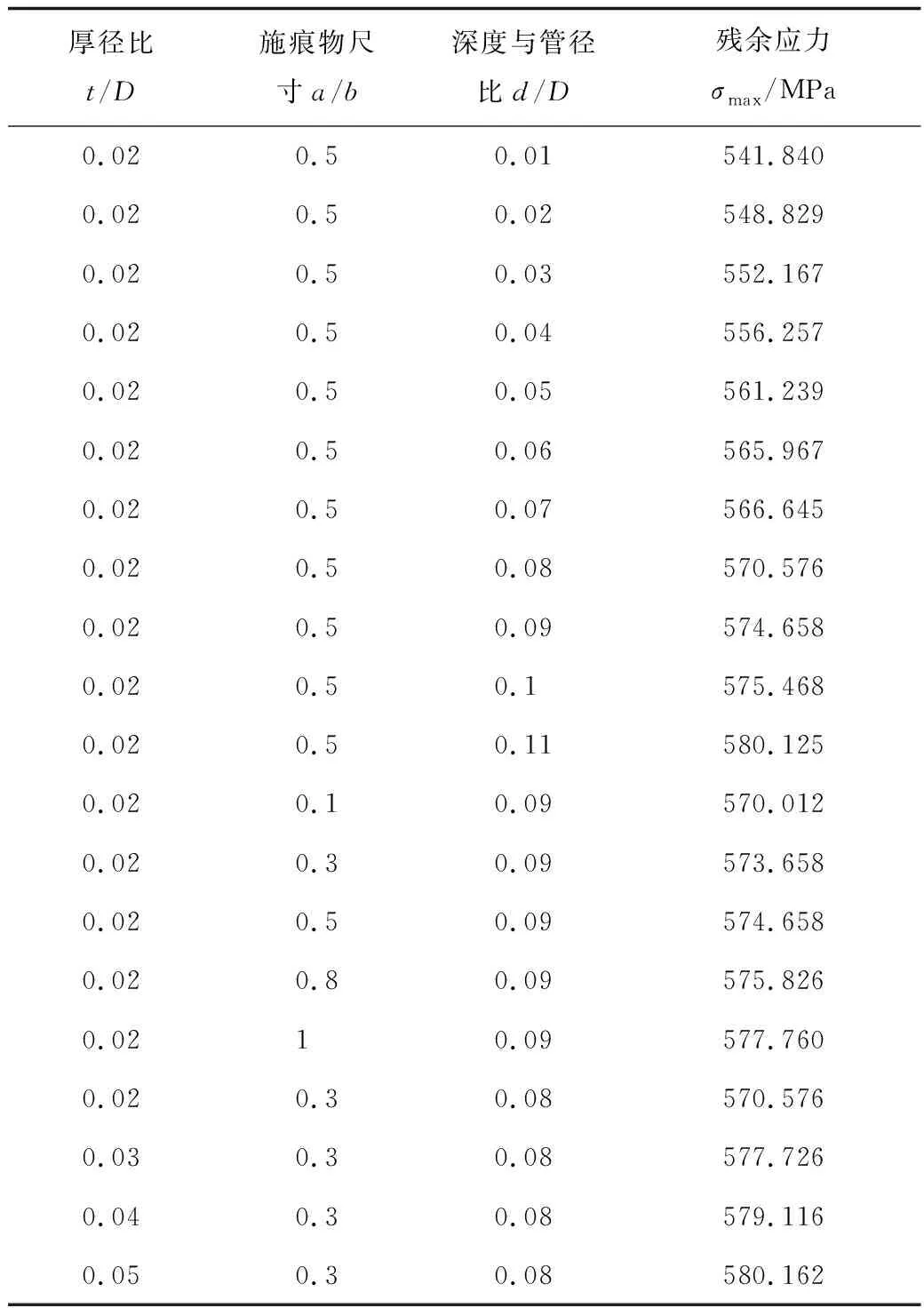
厚径比t/D施痕物尺寸a/b深度与管径比d/D残余应力σmax/MPa0.020.50.01541.8400.020.50.02548.8290.020.50.03552.1670.020.50.04556.2570.020.50.05561.2390.020.50.06565.9670.020.50.07566.6450.020.50.08570.5760.020.50.09574.6580.020.50.1575.4680.020.50.11580.1250.020.10.09570.0120.020.30.09573.6580.020.50.09574.6580.020.80.09575.8260.0210.09577.7600.020.30.08570.5760.030.30.08577.7260.040.30.08579.1160.050.30.08580.162

从表3可以看出，其他条件不变时，管道凹痕处残余应力随着凹痕深度的增加而增大。施痕物尺寸对残余应力的影响较小，随着施痕物尺寸的增大，应力不断增大，即在相同的管道壁厚和凹痕深度下，施痕物尺寸越大，残余应力也越大，但变化幅度较小。这是因为随着椭球体施痕物尺寸的增大，产生的凹痕区域也在不断增大，管道塑性变形的部分也越大，且凹痕区域的轮廓形状是不规则的，因此，残余应力会随着施痕物尺寸的增大而增大。在其他参数不变时，残余应力随着管道壁厚的增加而增大，开始增长较快，随后增长的幅度逐渐变缓。这是因为壁厚越厚，产生相同深度的管道凹痕所需的荷载越大，移除施痕物后凹痕处的残余应力也会越大。

3.1.2 椭球体长轴平行于管轴

模型中，管径D=1 000 mm；管道壁厚为t，mm；椭球体短轴为a，mm，长轴为b=500 mm；凹痕深度为d，mm。椭球体长轴平行管轴施加凹痕，计算算例与结果见表4。从表中可以看出，凹痕深度对残余应力影响较大，随着凹痕深度的增加，管道凹痕处残余应力不断增大。在相同的壁厚和凹痕深度下，残余应力随着施痕物尺寸的增大呈非线性增大。其他参数不变时，随着壁厚的增大，残余应力的变化开始增加较快，随后趋势变缓。

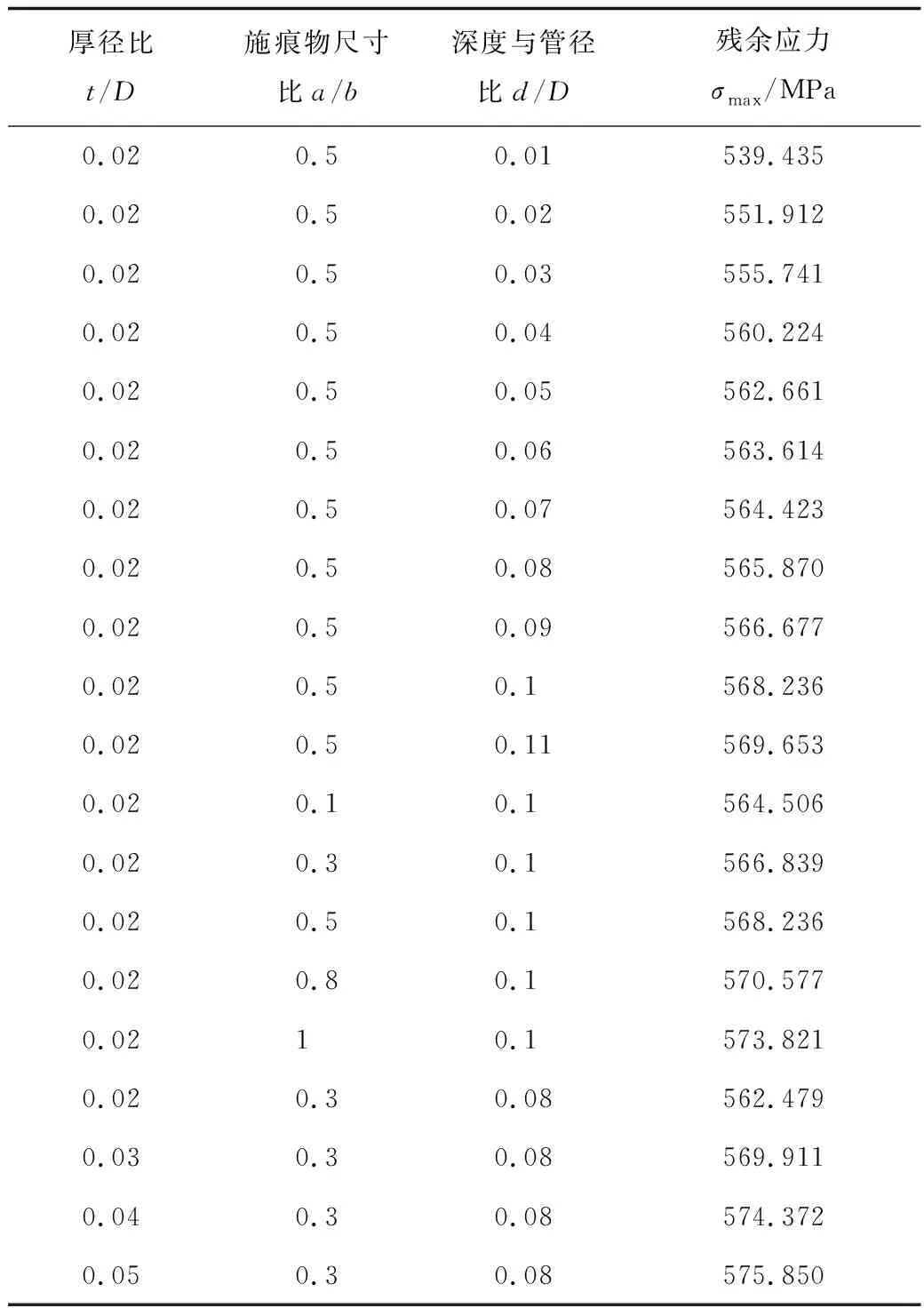
表4 椭球体(长轴平行于管轴)施痕物残余应力计算结果Table 4 Results of the residual stress of ellipsoid

3.2 圆柱体施痕物

管径D=1 000 mm；管道壁厚为t，mm；圆柱体半径为r，mm；圆柱体高h=500 mm；凹痕深度为d，mm，圆柱体底面垂直管轴施加凹痕，计算算例与结果见表5。从表中可以看出，管道凹痕处的残余应力随着凹痕深度的增加而增大。施痕物尺寸对残余应力影响较大，随着施痕物尺寸的增大，残余应力不断减小，开始减小较快，随后趋于平缓。这是因为施痕物尺寸越大，管道与施痕物的接触面积也越大，在相同的深度和壁厚下，凹痕处的残余应力也相应减小。随着管道壁厚的增大，残余应力不断增大，增大趋势趋于线性。

表5 圆柱体施痕物残余应力计算结果Table 5 Results of the residual stress of cylinder

3.3 矩形体施痕物

3.3.1 矩形体长垂直于管轴

管径D=1 000 mm；管道壁厚为t，mm；矩形体宽为u，mm，长v=400 mm，高w=200 mm；凹痕深度为d，mm，矩形体长垂直管轴施加凹痕，计算算例与结果见表6。从表中可以看出，其他参数不变时，管道凹痕处残余应力随着凹痕深度的增加而增大。在相同的壁厚和凹痕深度下，施痕物尺寸越大，残余应力越小。这是因为矩形体施痕物产生的是曲折凹痕，这类管道凹痕会出现应力集中现象，而随着施痕物尺寸的增大，应力集中会降低，所以残余应力也会相应减小。在施痕物尺寸和凹痕深度不变的情况下，残余应力随着壁厚的增加而增大，但变化幅度很小，变化不很明显。

表6 矩形体(长垂直于管轴)施痕物残余应力计算结果Table 6 Results of the residual stress of rectangle

3.3.2 矩形体长平行于管轴

管径D=1 000 mm；管道壁厚为t，mm；矩形体宽为u，mm，长v=400 mm，高w=200 mm；凹痕深度为d，mm，矩形体长平行管轴施加凹痕，计算算例与结果见表7。从表中可以看出，管道壁厚和施痕物尺寸不变时，管道凹痕处残余应力随着凹痕深度的增加而增大。其他参数不变时，施痕物尺寸越大，残余应力也越大。管道壁厚对残余应力影响较小，管道凹痕处的残余应力随着壁厚的增加而增大，但变化并不很明显，不同壁厚的凹痕管道之间的残余应力差距很小。

3.4 非线性回归分析

使用1stopt软件进行编程得到不同施痕物下凹痕管道残余应力的拟合公式。

表7 矩形体(长平行于管轴)施痕物残余应力计算结果Table 7 Results of the residual stress of rectangle

3.4.1 椭球体施痕物

根据对曲线观察和试算，选用幂函数形式：

(1)

式中：σmax为管道凹痕处最大残余应力，MPa；D为管径，mm；t为壁厚，mm；a为椭球体短轴长度，mm；b为椭球体短轴长度，mm；d为凹痕深度，mm；α，β，γ，δ为待定参数。

1)椭球体长轴垂直于管轴

椭球体施痕物下管道凹痕处残余应力公式：

(2)

图4为拟合公式结果与有限元结果的对比，公式的相关系数平方和R2为0.963，拟合效果较好。

图4 拟合公式与有限元结果对比Fig.4 Results comparison between formula fitting and FE

2)椭球体长轴平行于管轴

椭球体施痕物下管道凹痕处残余应力公式：

(3)

图5为拟合公式结果与有限元结果的对比，公式的相关系数平方和R2为0.974，拟合效果好。

图5 拟合公式与有限元结果对比Fig.5 Results comparison between formula fitting and FE

3.4.2 圆柱体施痕物

根据对曲线的观察和试算，选用幂函数形式：

(4)

式中：r为圆柱体半径，mm；h为圆柱体高度，mm。其他参数定义与公式拟合方法与3.4.1节一致。

圆柱体施痕物下管道凹痕处残余应力公式：

(5)

图6为公式拟合结果与有限元结果的对比，公式的相关系数平方和R2为0.958，拟合效果较好。

图6 拟合公式与有限元结果对比Fig.6 Results comparison between formula fitting and FE

3.4.3 矩形体施痕物

根据对曲线观察和试算，选用指数函数形式：

(6)

式中：u为矩形体宽度，mm；v为矩形体长度，mm；其他参数定义与公式拟合方法与3.4.1节一致。

1)矩形体长垂直于管轴。

矩形体施痕物下管道凹痕处残余应力公式：

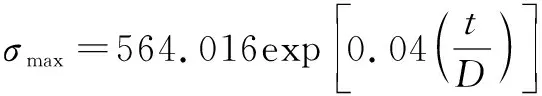
(7)

图7为公式拟合结果与有限元结果的对比，公式的相关系数平方和R2为0.954，拟合效果较好。

图7 拟合公式与有限元结果对比Fig.7 Results comparison between formula fitting and FE

2)矩形体长平行于管轴

矩形体施痕物下管道凹痕处残余应力公式：

(8)

图8为公式拟合结果与有限元结果的对比，公式的相关系数平方和R2为0.952，拟合效果较好。

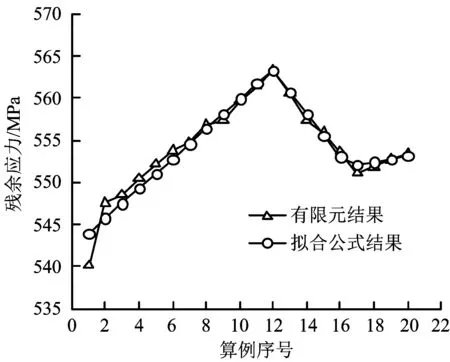
图8 拟合公式与有限元结果对比Fig.8 Result comparison between formula fitting and FE

应当注意的是以上得出的表达式是在假定其余参数不变的特定条件下成立，其适用范围有限。

4 结论

1) 通过R.Akbari Alashti等的实验验证了利用有限元模拟能够有效反映不同施痕物下管道凹痕的形成过程，因此，利用有限元模拟的计算结果来对凹痕管道的残余应力进行研究是合理的。

2) 施痕物为椭球体，其他参数不变的情况下，管道凹痕处残余应力随着凹痕深度的增加而增大，随着施痕物尺寸和管道壁厚的增大而增大。因此，在工程中要注意这类凹痕的残余应力对管道的影响。采用幂函数拟合了残余应力与各参数之间的关系。

3) 施痕物为圆柱体，其他参数不变，管道凹痕处残余应力随着凹痕深度的增加而增大，随着施痕物尺寸的增大而减小，壁厚对残余应力影响较小，不同凹痕管道的残余应力之间只相差很小的数值。采用幂函数拟合了残余应力与各参数之间关系。

4) 施痕物为矩形体，相同条件下，管道凹痕处残余应力随着凹痕深度的增加而增大，随着施痕物尺寸的增大而减小。管道壁厚的变化对残余应力几乎没有影响。工程中应该尽量避免这类曲折凹痕的产生，因为会产生严重的应力集中现象。采用指数函数拟合了残余应力与各参数之间的关系。