基于损伤累积模型的可靠度保守估计方法

丁 然，李 强

(北京交通大学 机械与电子控制工程学院，北京 100044)

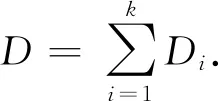
理论上，中心极限定理是对载荷谱级数k→∞ 时和分布的近似，但实际应用中载荷谱通常只有8级或16级.若近似计算产生非保守误差，在可靠度要求较高的场合，该计算方法的应用受到限制.而分析中心极限定理的近似误差保守与否通常存在一定的困难.另一方面，为获得每级载荷下的损伤分布，可能需要用额外的实验数据进行参数估计.但可靠性问题通常关注的是拖尾，即高可靠度区的损伤分布特性，并非均值附近的分布特征.这意味着需要大样本的数据才能获得高置信度的参数估计.

针对上述问题，本文提出一种通过代数和对损伤或疲劳寿命可靠度进行保守估计的方法.损伤分布已知时，此方法可直接用于概率损伤模型；损伤分布未知时，此方法可基于一般的P-S-N(P为失效率，S为应力幅，N为寿命)曲线进行总损伤计算，从而避免额外的参数估计.本文方法计算简便且可得到保守的可靠度估计，便于工程应用，但通常只能对高可靠度区损伤或寿命的可靠度进行保守估计.

1 可靠度的保守估计条件

设D为随机变量，则其可靠度R的估计值d满足P(D≤d)=R(P为概率)，即d是D的R可靠损伤.如果P(D≤d)≥R，则称d是R可靠损伤的保守估计，或R是d的可靠度的保守估计，下文均采用后一种说法.

一个损伤累积模型可给出保守估计是指该模型满足如下条件：给出各级载荷下R可靠损伤的保守估计di，则总损伤d=∑di也为保守估计，即

P(Di≤di)≥R⟹

(1)

下面讨论式 (1)成立的条件.

先讨论两级加载，即k=2 的情况.设Di的累积分布函数(Cumulative Distribution Function,CDF)和概率密度函数(Probability Density Function,PDF)分别为Fi(x)和fi(x)，且两级损伤相互独立.则D的CDF可利用全概率公式计算：

(2)

因Fi(x)是单调函数，令u=F1(x)，v=F2(y)，则du=f1(x)dx，dv=f2(y)dy.取d=d1+d2，代入式(2)得

(3)

式 (3)表明D≤d1+d2的概率等于Ouv平面内被积函数下方区域的面积，如图1中的阴影区域所示.在给定可靠度，如R=0.8 时，若计算得积分面积不小于 0.8，则模型可给出保守估计.

图1 保守估计的几何解释Fig.1 Geometric illustration of conservative estimation condition

由于di是R的函数，所以式(3)中被积函数是u和R的函数：

(4)

令曲线下方的面积为Π(R)，则有

(5)

式 (1)成立等价于Π(R)≥R.

(6)

2 常见损伤分布的保守估计条件

目前的损伤累积模型均假设各级载荷下的损伤服从仅参数不同的同族分布.上节讨论的一般模型不受此假设的限制.为将本文理论应用到已有的概率损伤模型，下文针对一些常见的分布族计算其可靠度保守估计的具体条件.

2.1 指数分布

损伤服从指数分布，即Di～Fi(x)=1-exp(-x/θi),x≥0，其中θi为尺度参数.则有

(7)

将式(7)代入式 (6)和 (5)得

(8)

图2为η=1时的Π(R)图像，图中Rp为方程Π(R)=R的解，可利用数值方法求得.可以看出，当R≥Rp时，式(1)成立.图3为η取不同值时Rp的变化趋势.可以看出，η=1 时Rp的最大值约为 0.715 3.工程应用中，即使分布参数的取值未知，也可用R≥0.715 3 获得总损伤的保守估计，本文称满足此特点的条件为一致可用的保守估计条件.

图2 Π(R)与R的关系图Fig.2 Relationship between Π(R)and R

图3 Rp与η的关系图Fig.3 Relationship between Rp and η

2.2 对数正态分布

损伤服从对数正态分布，即Di～Φ[(lnx-μi)/σi] (x>0)，其中Φ(x)为标准正态分布的CDF；μi为对数均值；σi为对数标准差.lnx-μi=ln[x/exp(μi)]，所以exp(μi)是尺度参数，按本文约定η=exp(μ1-μ2).由于求解Π(R)≥R时需考虑σ1、σ2和η不同取值的组合，所以对数正态分布下的求解与指数分布下的求解具有明显区别.参数较多时，若没有一致可用的保守估计条件，将大大增加工程应用的难度.

视Rp为参数的函数，观察Rp(σ1,σ2,η)的计算结果发现，当σ1≤σ2时，Rp是η的增函数，如图4所示.此外，无论η取何值，Rp是σi的增函数.取σ=max{σ1,σ2}，则有

Rp(σ1,σ2,η)≤Rp(σ,σ,η)≤Rp(σ,σ,1)

(9)

利用上式可计算仅与σ相关的保守估计条件.

图5为η=1时Rp的图像.可以看出，Rp为σ的增函数，σ=1时Rp略小于 0.8.

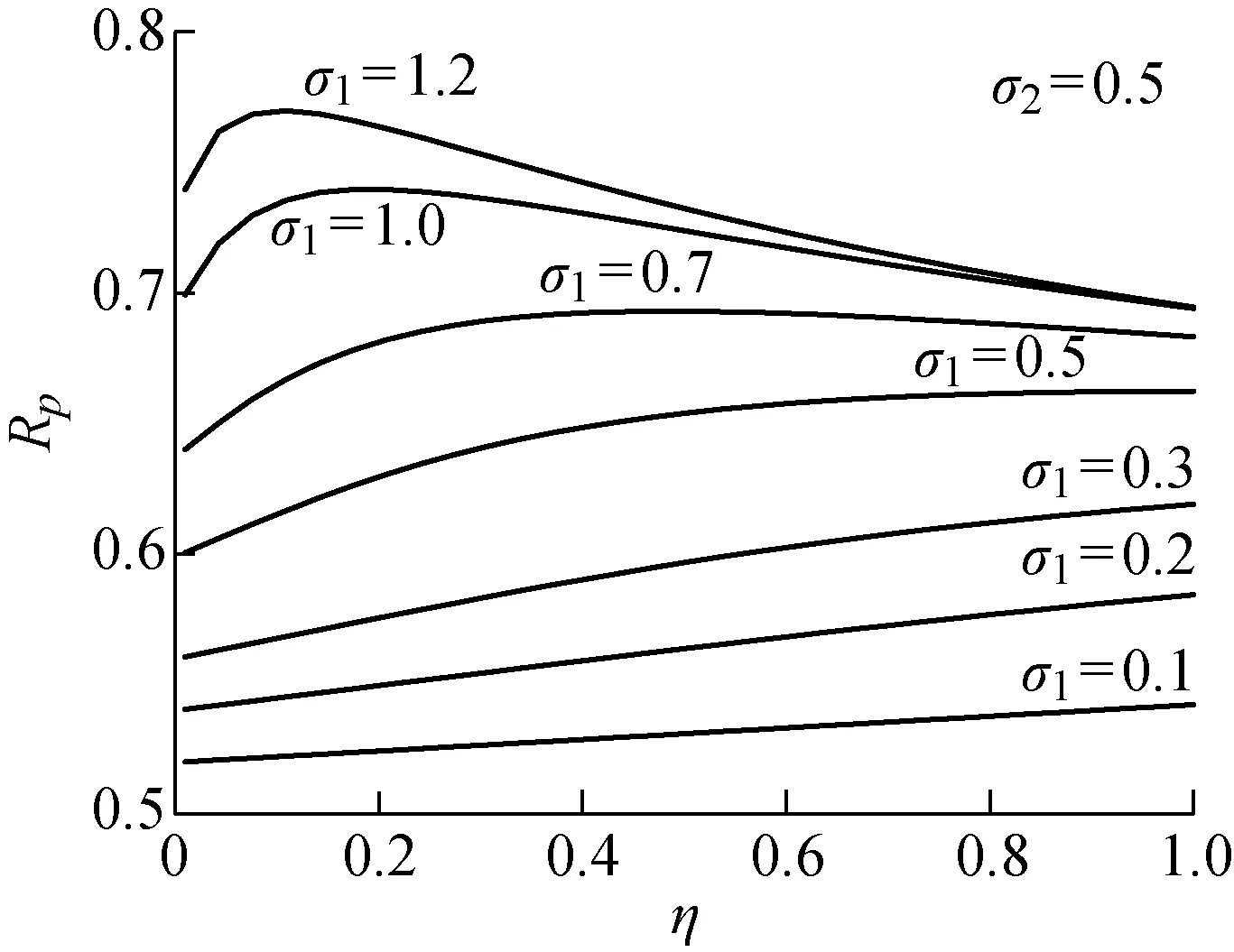
图4 Rp 与η的关系图Fig.4 Relationship between Rp and η

图5 Rp与σ的关系图Fig.5 Relationship between Rp and σ

损伤服从对数正态分是应用本文理论计算保守估计条件的典型例子，有以下几点需要说明：

(1)Rp并不总是η的增函数.对于复杂的分布，要考虑各个参数对总损伤分布的影响.

(2)对于较大的σ，保守估计的条件可能很苛刻.如σ=2 时Rp≈0.95，此情况建议使用其它方法估计可靠损伤.

(3)通常损伤的对数标准差小于 1，此时可一致使用R≥0.8 进行保守估计.

2.3 其他常见分布

经计算可知，当损伤分布服从正态分布时，总有Rp=0.5.故可一致使用R≥0.5进行保守估计.

实践表明，当损伤服从Weibull分布时，不同载荷下损伤分布的形状参数(β)为常数，即β1=β2=β.由于Rp是β的减函数，所以β≥1时，可一致使用R≥0.715 3进行保守估计.

负Weibull分布也称第3型广义极值分布，目前很少用于损伤建模.但 Castillo[6]的理论研究表明，在相对一般的条件下损伤必然服从第3型广义极值分布，因此该分布有较高的理论价值，此时Rp是β的增函数，当β≤10 时，可一致用R≥0.578 2进行保守估计，当β≤3.5 时，总有Rp≤0.5.此外，当β增大时，Rp的增大并不明显，如果损伤服从此分布有必然性，则此特性可从统计学角度解释为何 Miner法则总能给出偏差不大的损伤估计.

表1为常见分布的一致可用保守估计条件.

表1 常见分布的一致可用保守估计条件Tab.1 Uniform conditions of conservative estimation for common distributions

3 应用举例

上文讨论的仅为两级加载情况下保守估计成立的条件.原则上，本方法可以推广到k级加载的情况，但k级加载要计算多重积分，因此计算效率较低.由正态分布的可加性知，无论k取何值，总有Rp=0.5.若损伤服从其它分布，当k→∞ 时，根据中心极限定理，D依分布收敛于某正态分布，从而Rp收敛至 0.5.以损伤服从Weibull分布为例，对应k=2，3，4以及ηi=1时Rp的计算结果见表2.可以看出，当Rp>0.5 时，Rp为k的减函数.因此，无论k取何值，总可一致使用k=2 时的条件进行可靠度保守估计.而Rp≤0.5 时总可使用R≥0.5 来进行保守估计.

分别采用Miner线性损伤模型和Zhu等[7]的损伤模型进行损伤计算.由文献[7]中数据估得某钢材的S-N曲线的方程为

NS7.01=2.45×1024

(10)

文献[7]认为在恒幅载荷下材料的寿命服从对数正态分布(LN)，即

N～LN(μN,σN)

(11)

式中:μN为对数均值，μN=logN，可由式 (10)计算而得.为简化计算，本文假设变异系数(γ)不随S变化，γ=σN/μN.由文献[7]中数据估得γ=0.054 9.文献[7]进一步推导出恒幅载荷循环作用n次所得损伤D(n)也服从对数正态分布：

(12)

表2 Rp随k的变化Tab.2 Variation of Rp with k

表3 不同可靠度下损伤的计算Tab.3 Damage calculations under different reliability

由表1可知，对数正态分布的可靠度保守估计条件为R≥0.8.即按80%和90%可靠度计算的损伤是保守的(偏大)；而按50%或按传统Miner法则计算的损伤则偏小.假设损伤服从对数正态分布，则按 Monte-Carlo 法模拟的 90%，80%，50% 的可靠损伤分别为 0.222，0.193，0.150，还可用∑n/∑D进行可靠寿命的大致估算.如本例对应 Miner 法则、Zhu模型和 Monte-Carlo 模拟估得的80%可靠寿命分别为8.46×106、10.06×106和11.44×106，从而验证了本文方法的保守性.

图6为k=6时，Monte-Carlo法计算得出总损伤的实际分布和中心极限定理(CLT)计算得出渐近分布的对比.可以看出，渐近分布与实际分布较为接近.但在可靠度要求较高的区域，如R≥0.9 时，渐近分布给出的可靠度高于实际分布.这意味着用渐近分布进行可靠度评估无法保证计算结果的保守性.

图6 k=6时Monte-Carlo模拟结果与CLT结果的对比Fig.6 Comparison between the results calculated by Monte-Carlo method and CLT while k=6

本文的出发点是在各级损伤分布已知的情况下进行总损伤的可靠度估计.目前已有许多概率化的累积损伤模型，结合这些模型为损伤建模后即可应用文本方法对可靠度进行保守估计.

具体应用时，由于对损伤的参数进行统计推断可能会产生误差，所以本文推导了一些常见分布一致可用的保守估计条件.只要采用的分布对损伤有较好的拟合优度，即使其参数估计有一定出入，也不影响其保守推断.

此外，无论使用本文方法还是中心极限定理，都要求各级载荷下的损伤相互独立.若认为损伤间存在依赖关系，如不同的加载顺序对总损伤有较大影响，则需使用其它方法进行可靠度估计.

4 结语

统计学角度认为Miner 法则总可以给出偏差不大的损伤均值估计.但理论推导和数值算例表明，直接使用 Miner 法则或中心极限定理等方法求得的总损伤可能是非保守的，因此其在可靠度要求较高的应用中受到限制.

当损伤服从的分布已知时，往往存在一致可用的保守估计条件.利用这类条件进行计算，可避免分布参数估计误差对可靠度保守性带来的影响.损伤分布的这种特性对减少甚至避免额外的参数实验有很大作用，因此本文研究有较好的理论意义和实际应用价值.