GPS/INS延时估计与基于残差重构的延时补偿算法

付廷强，马太原，王亚飞，殷承良

(上海交通大学 机械与动力工程学院，上海 200240)

随着人们对减小交通的事故发生率，将人类从疲劳的驾驶工作中解放出来的需求发展，自动驾驶成为了当下的研究热点，而车辆的定位导航则是实现自动驾驶的前提和基础.车辆定位导航的方式有很多种，可以大体分为单传感器定位如视觉定位[1-2]、卫星定位[3-4]以及多传感器组合定位[5-6]等.其中，全球定位系统(GPS)/惯性导航系统(INS)的组合导航系统比较成熟，由对多种自动驾驶车辆的传感器配置的统计结果[7]可以看出，GPS和惯性测量单元(IMU)几乎是必备的2种传感器.两者具有较强的互补特性，组合后既可以通过INS的高采样速率和自主式导航的特性解决GPS采样速率低和易失锁的问题，又可以通过良好环境下精确的GPS信号去除INS的累积误差.

但是，多传感器进行信息融合时总是会受到时延上的困扰，在对时延进行补偿方面，现有研究思路大体可分为以下几种：把存在延时的状态作为扩展量添加到状态方程中，扩展维数与延迟步数相关，因此适合于延时不是太大的情况[8]；根据延迟的观测量或残差值构造当前时刻的伪观测量或伪残差值，利用构造的量进行测量更新[9-10]；利用延时的测量值估计出延时的状态量和延时值，然后运用运动学或动力学关系构造方程计算现在的状态[11-12].GPS/INS组合导航系统面临相同问题，根据文献[11]和[12]对延时问题的研究，GPS接收机的数据处理过程给GPS输出引入了可达百毫秒级的延时，该问题会影响组合导航的精度.

许多文献对GPS和INS融合过程中的延时问题进行了分析，并提出了一些延时补偿的方法.文献[13]基于对测量残差的观测，分析了GPS测量值发生延时的情况下实现组合导航滤波稳定的条件.文献[14]构建了时间同步误差模型，并采用Lagrange插值法获取对应于任意延时值的IMU数据，消除延时的影响.文献[15]提出了高动态运动条件下软硬件相结合的时间同步策略,比较适用于飞行器等大机动运载体.文献[11]构建了非线性观测器，获得延时的导航解及延时值，并通过运动学关系估计当前时刻的导航解.考虑到车辆相对于飞机等运载器的运动强度低得多，不需要精密的硬件时间同步装置，因此本文以软件的方式进行时间同步.

区别于以上方法，本文的特色在于直接对卡尔曼滤波器进行适应性修改，利用残差重构的方式实现延时补偿.首先构建车辆的GPS/INS松耦合组合导航模型，然后根据运动学关系对模型做了一定的修改并实现延时估计，最后将残差重构算法应用到GPS/INS组合导航滤波中实现了延时误差补偿，并通过试验验证了所述算法的有效性.

1 GPS/INS组合导航模型

构建GPS/INS组合导航模型是完成位置解算至关重要的一步，组合导航的数学模型包括状态模型和测量模型.本文在构建模型时采用的导航坐标系(n系)为北东地坐标系；采用的载体坐标系(b系)x轴指向车辆前方，y轴指向车辆的右侧，z轴向下；下标i表示惯性坐标系；下标e表示地心地固坐标系.

状态模型为

(1)

测量模型为

y=Hx+V

(2)

式中：x为状态矢量；F为系统矩阵；W为估计噪声；y为观测量；H为测量矩阵；V为测量噪声.状态模型描述了惯性解算过程中位置、速度、角度、加速度计和陀螺仪误差状态的微分形式，而测量模型则描述了观测量与误差状态之间的关系.

1.1 状态模型

车辆在平直路面上的行驶过程中，沿着地向的加速度可以视为白噪声，因此没有必要估计车辆沿着地向的速度误差状态以及位置误差状态.误差状态矢量

(1)平台失准角微分方程.平台失准角微分方程描述了计算导航坐标系相对于实际导航坐标系的角度偏差.产生偏差的主要原因是由于车辆在运动过程中所参考的导航坐标系在不停移动，这造成了实际导航坐标系相对于计算导航坐标系发生偏转，同时陀螺仪的漂移也会为角速度的测量引入误差.

(3)

式中：

ψ=(ψx,ψy,ψz)

(2)速度误差微分方程.速度误差主要是由平台失准角和加速度计漂移引起的，平台失准角的存在导致比力不能正确变换到导航坐标系下.

(4)

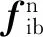
(3)位置误差微分方程.位置误差主要由速度误差引起，如果不及时校正，误差会逐渐积累，最终造成较大的定位误差.

(5)

(6)

式中：RN为车辆所处地点的子午圈曲率半径；RE为车辆所处地点的卯酉圈曲率半径；hb为车辆所处地点的高度.

(4)加速度计和陀螺仪偏差.传感器的零偏是导致惯性传感器输出误差的重要因素,惯性传感器的零偏可以建模为一阶Gauss-Markov过程.

(7)

式中：τa和τg分别为加速度计和陀螺仪零偏的相关时间；Wba和Wbg分别为加速度计和陀螺仪零偏的噪声项.

由以上的讨论可见，这些误差是相互耦合的，只有对这些误差状态全部正确估计，才能得到较好的导航结果.根据式(3)～(7)即可完成组合导航状态模型即式(1)的建模，具体的建模推导过程可以参考文献[16].

1.2 测量模型

对于卫星接收机而言，接收机的位置和速度易获取，在松耦合组合导航方程中，选取INS与GPS的位置差及速度差作为松耦合组合导航 Kalman 滤波中的观测量.

(1)INS与GPS的位置差

式中：LI和LG为INS和GPS输出的纬度值；λI和λG为INS和GPS输出的经度值；Nx和Ny为GPS接收机沿着导航坐标系x和y方向的距离测量误差.由于RN和RE随着车辆位置不断变化，为了使观测噪声不受车辆位置变化影响，式(8)和(9)可以改为

(LI-LG)(RN+hb)=δLb(RN+hb)+Nx

(10)

(λI-λG)(RE+hb)cosLb=

δλb(RE+hb)cosLb+Ny

(11)

(2)INS与GPS的速度差

由式(10)～(13)可获得测量矩阵

根据以上方程构建模型后，对状态模型和测量模型进行离散化,以实现由k-1步的状态值估计第k步的状态值.将式(1)和(2)离散化之后得

(14)

式中：φk-1=eFτ(τ为IMU采样时间间隔)；Hk=H；Q为系统噪声协方差矩阵，由文献[16]所述方法计算得到.

2 延时量的估计

图1简要描述了GPS/INS组合导航系统中传感器采样过程，Tl为GPS采样时间间隔，Ts为INS输出导航时间间隔.根据GPS接收机延时问题的研究[12]，接收机输出数据的延时大约为数百毫秒，文献[11]测试了u-blox LEA-6T接收机，延时值为150 ms左右，造成的影响不容忽视.

图1 考虑时延的数据融合Fig.1 Data fusion considering the delay

文献[14]从运动学角度推导了GPS的位置测量值与延时量之间的关系，并考虑GPS延时影响，对GPS/INS松耦合组合导航的状态模型和测量模型进行相应修改.本文在文献[14]的基础上，继续推导了GPS速度测量值与GPS延时量之间的关系.

(15)

将δTd作为扩展状态进行估计后，式(14)中的状态方程应改写为

(16)

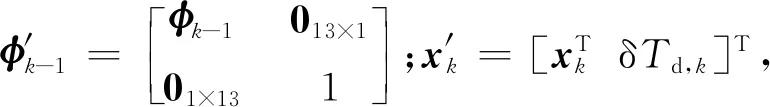
进行误差状态矢量扩展之后，相应测量方程的测量矩阵也应发生改变.时延会对GPS速度和位置测量值的准确性产生影响，如图1所示，GPS在t时刻的采样实际对应着t-Td时刻的GPS测量值.假设车辆在t时刻的真实速度函数和位置函数为v(t)和p(t)(为了表达简洁，这里省去了上下标)，则t-Td时刻对应的真实速度和位置为v(t-Td)和p(t-Td).t时刻GPS对速度和位置的测量值为vG(t)和pG(t)，测量误差分别为ξ和N.由式(15)及以上表述，t时刻GPS的测量值可以表示为

在测量方程中，将INS与GPS的位置差及速度差作为观测量，根据式(17)～(20)对延时状态下INS和GPS观测量的表达，继续将速度差和位置差作为观测量，可以得到扩展状态后的测量矩阵应为

3 基于残差重构的延时补偿

计算伪观测值是进行延时补偿的一种重要方法，在Kalman滤波过程中，根据测量值计算得到的残差进行测量更新，因此伪观测值可用伪残差值来代替.本文根据文献[10]对延时问题和残差重构方法的研究，设计了针对GPS/INS组合导航系统的延时补偿算法，利用伪残差值来弥补延迟的GPS测量值.

测量残差方程和估计误差方程是推导残差传播方程的两个基本方程，

测量残差：

(21)

估计误差：

(22)

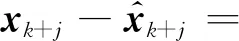
(I-Kk+jH)φk+j-1ek+j-1

(23)

式中：Kk+j为Kalman滤波中的增益矩阵；I为计算过程中产生的单位矩阵.测量残差可以由估计误差得到

(24)

将式(23)不断循环代入式(24)，即可获得残差传播方程

εk+j=Hφk+j-1ek+j-1=

Hφk+j-1(I-Kk+j-1H)φk+j-2…

φk(I-KkH)φk-1ek-1=

Hφk+j-1(I-Kk+j-1H)φk+j-2…

φk(I-KkH)H-1Hφk-1ek-1=

Hφk+j-1(I-Kk+j-1H)φk+j-2…

φk(I-KkH)H-1εk=

(25)

式中：

Ak+m=Hφm(I-KmH)HT(HHT)-1

若由惯性导航方程计算并输出导航解的周期为Ts，而GPS输出测量值的周期为Tl，则由延时引起的采样步数误差为kd=Td/Ts.假设当INS运行到第k步时，GPS接收机输出了测量值，则残差重构算法可以按如下方式运行.

(1)将GPS输出的测量值与存储的第k-kd步INS数据进行融合，并计算获得第k-kd步的残差：

(2)计算残差传播方程，将第k-kd步的残差向第k步传播，获得当前时刻的伪残差值：

(3)计算当前时刻的Kalman增益，根据计算得到的测量残差，通过测量更新获得误差状态矢量，将误差状态反馈得到当前时刻导航解.当GPS再次输出测量值时返回第(1)步.

运行完第(1)和第(2)步后完成了伪残差值的重构，运行完第(3)步后完成基于伪残差值的更新，从而完成了整个延时补偿过程.具有延时估计和补偿功能的GPS/INS组合导航卡尔曼滤波器设计可以参考图2.

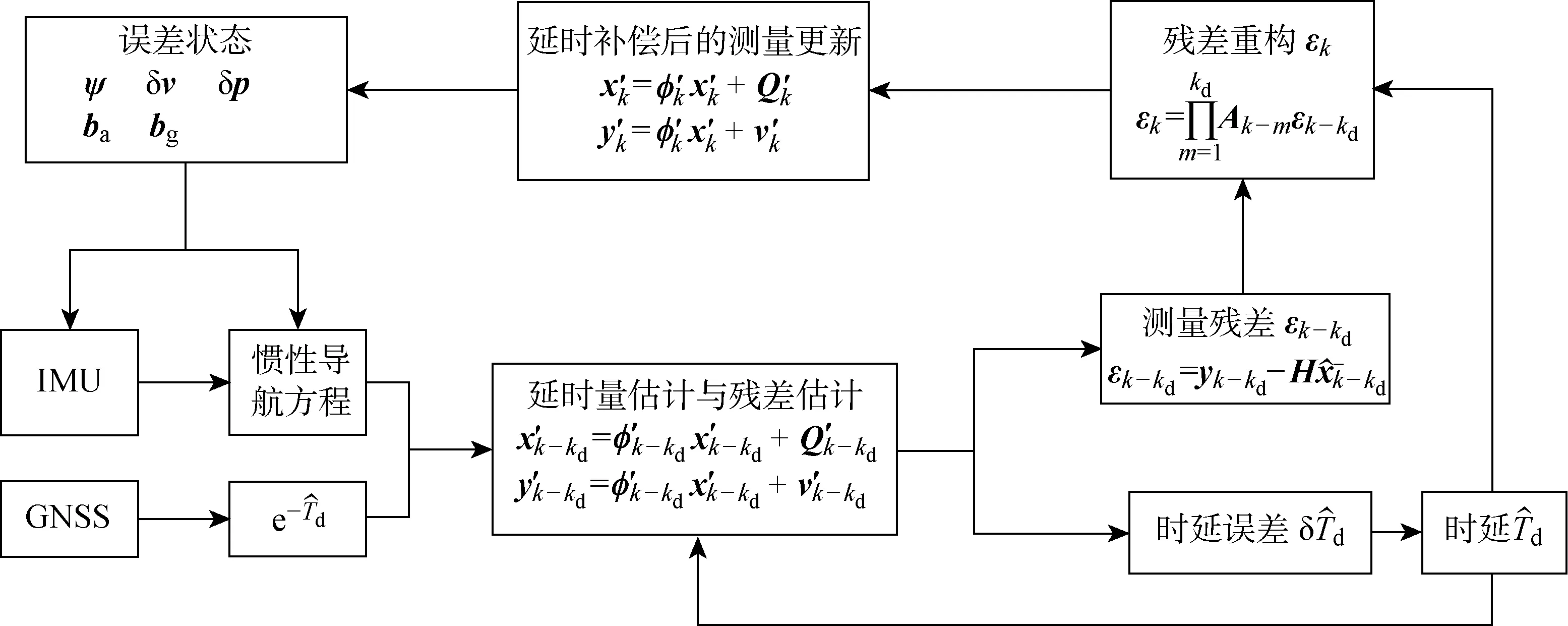
图2 具有延时补偿功能的组合导航系统设计Fig.2 Design of integrated navigation system with delay compensation

4 试验结果分析

数据来源为西班牙马拉加大学MAPIR实验室采集的数据集，该数据集主要用于研究车辆运行中的多种方式定位导航，具体的数据说明文档可以参考文献[17].该数据库不仅提供了完整的采集数据，还为开发者提供了轨迹真值，因此常被用于定位研究.本次实验选取的IMU数据来源于Xsens公司生产的MTi系列惯性测量单元，采样频率为100 Hz，GPS数据由一个消费级的GPS接收机采集，采样频率为1 Hz，所有采集数据均经过精确时间同步.车辆在马加拉大学校园内进行数据采集工作，图3展示了车辆的运行轨迹.

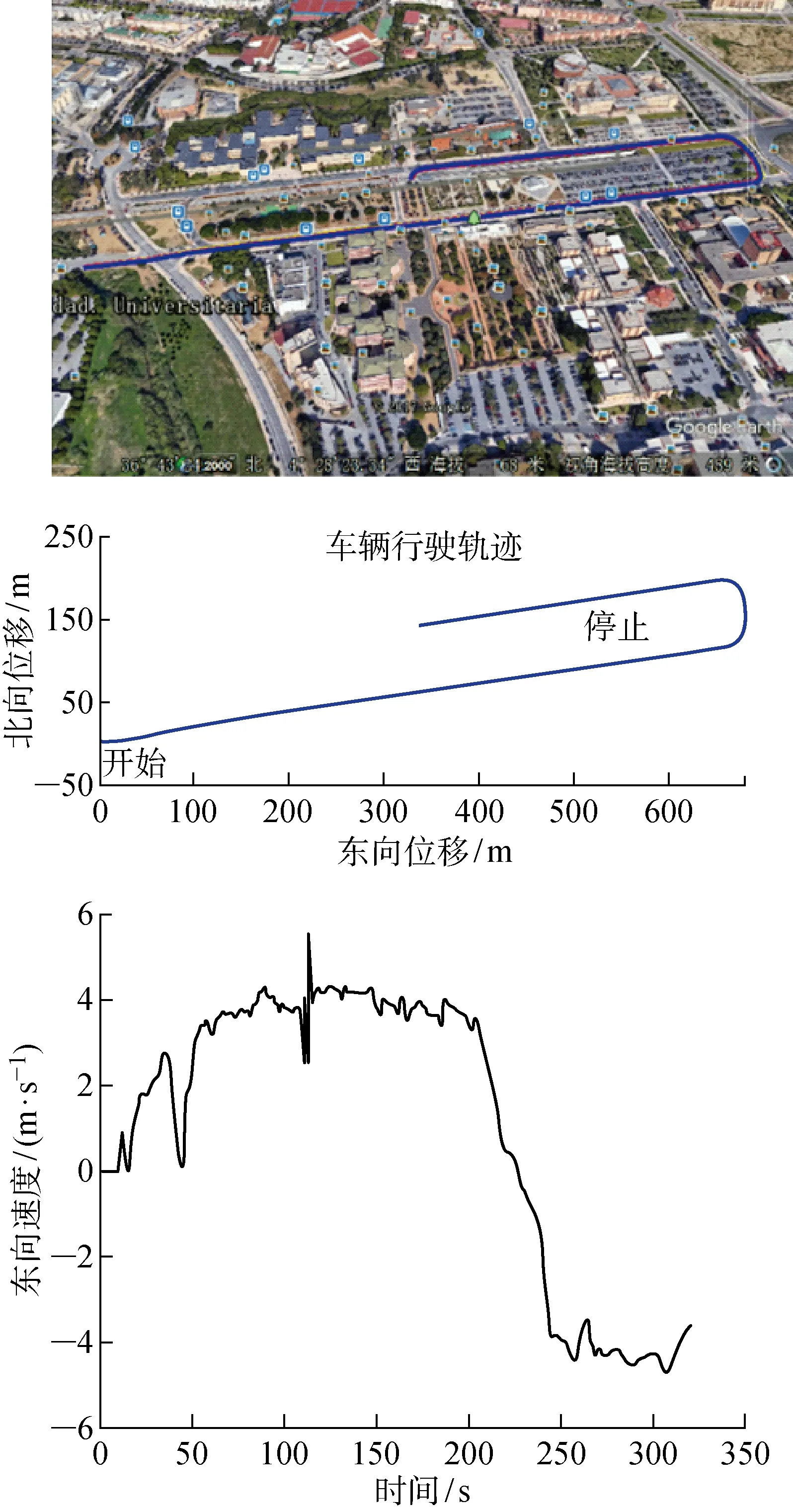
图3 车辆运动轨迹及东向速度变化Fig.3 Vehicle trajectory and eastward velocity

由于整个过程中车辆大致向东运动，因此对车辆的东向速度进行分析比北向更具代表性和价值.由图3中东向速度可看出车辆是由静止开始启动的，中间出现数次加减速和一次大的转向，多种工况的存在满足了实验所需条件.

4.1 GPS延时产生的影响分析

为研究GPS延时对导航效果的影响，本实验特意给原本经过校准的GPS数据分别添加了100，200，300 ms的延时偏差.图4为加入时延偏差后GPS/INS组合导航系统测得东向速度误差(Δx)和东向位置误差(ΔL)及相应方均根误差eΔx和eΔL的变化情况.

图4 不同延时条件下的定速定位误差Fig.4 Velocity and positioning error with different time delays

由图4可见，在速度变化剧烈处(即110 s左右)，速度误差及均方根误差均表现出明显增加，而位置误差表现出明显的速度相关性，车辆速度越大，相应的位置误差也会越大，位置均方根误差随着时间的增加逐渐趋于平稳；随着延时时间的增加，车辆的东向速度、位置误差和均方根误差均出现了明显增加.

4.2 延时估计与补偿算法的有效性验证

为了验证延时误差估计算法的准确性，应用该算法对上述加有延时偏差的GPS数据进行延时估计，对于不同延时值的估计结果如表1所示，估计误差均在5 ms内，因此延时估计算法可以较好地估计出GPS数据的延时值.

为了验证残差重构算法能否较好地实现延时补偿，当具有200 ms延时偏差的GPS数据与INS数据进行融合时，利用延时估计和残差重构算法进行延时估计和补偿.作为对比，对于具有100，300 ms延时误差的GPS数据不作任何处理.

表1 延时估计值Tab.1 Estimation of the time delay

图5描述了对200 ms延时误差进行补偿后的速度和位置误差及均方根误差的变化.对比图4和5，有200 ms延时的GPS数据与INS数据融合时，用残差重构的方式进行了延时补偿后，其位置、速度的误差和均方根误差有了明显减小.由图5可见，对200 ms延时量数据进行延时补偿后，其定位定速误差甚至比未进行补偿的100 ms延时量数据表现得更好.其中，速度误差及均方根误差降低明显，已接近0，位置误差及均方根误差在50 s后也逐渐减小并趋于平稳.因此，该算法对GPS/INS组合导航的延时估计和补偿有着显著效果.

图5 对200 ms延时进行补偿后的定速定位误差Fig.5 Velocity and positioning errors after delay compensation in 200 ms delay case

5 结语

数据处理过程会给GPS数据引入较大时延，这对导航精度造成不利影响，本文通过分析GPS时延给组合导航系统定位和定速引入的误差，提出了一种延时估计和补偿算法，并对传统的GPS/INS松耦合组合导航滤波器进行修改.结果表明，该算法可以较好地估计GPS延时值，并有效地减小组合导航中由时延引入的误差.本文算法对实际工程中处理GPS/INS组合导航系统或其他多传感器融合的延时问题具有指导意义.