各向同性分子磁体的电导特性
2019-11-04闫红叶牛鹏斌
闫红叶,牛鹏斌
(山西大同大学物理与电子科学学院,山西大同037009)
单分子磁体具有大自旋和磁性各向异性的特点,在过去的二十多年里,我们已经展示了它的一些基本特性,比如宏观量子相干性[1-2]和宏观量子隧道[3]等。由于这些磁性宏观量子效应的研究,使得单分子磁体的宏观量子效应一直倍受期待,同时人们希望将单分子磁体应用到分子电子学[4-5]中,特别是量子计算[6]等。自从单个磁性分子Mn12 被发现可以制备在典型的场效应晶体管几何中,就意味着可以在单分子磁体上测量量子输运,人们便开始为单分子磁体的电子输运和自旋输运付出巨大的努力,通过它的传输属性观察到或者理论上预测到的,如负微分电导[7-8]、近藤效应[9-11]等。但是,对于天然的单分子磁体[12]的进一步研究也是有一些困难的,因为它的参数是无法改变的,所以早在20 世纪80年代就被人工可以合成了。
在本文,我们利用电流和电导,电流和格林函数之间的关系,推倒出了各向同性人工分子磁体在顺序隧穿区的单占据本征态占据几率和电导随门电压的变化关系式及给出它们之间的关系图。
1 模型和计算方法
我们给出如下的输运模型,总的哈密顿量:H=HLeads+HT+HASMM。第一项表示金属电极的空穴载流子,第二项HT=表示电极与人工分子磁体之间的耦合,tkα为耦合强度。第三项表示人工分子磁体的哈密顿量

其中,U表示空穴与空穴之间的库伦排斥能。Sz,±为空穴的自旋算符,Sz,±为大自旋算符,两者之间的耦合是各项异性的,用γ来描述。在本文我们考虑一种特殊情况,即γ=1(表示各向同性)且U→∞(即空占据态N=0,单占据态N=1)。那么相应的本征态和本征值如下:

N=1:全极化态本征态和本征值为:
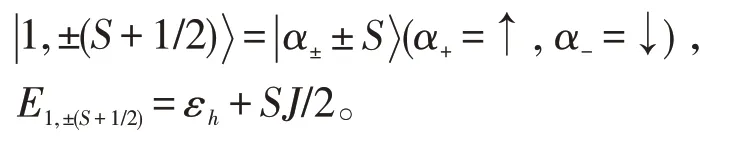
耦合态本征态和本征值为:
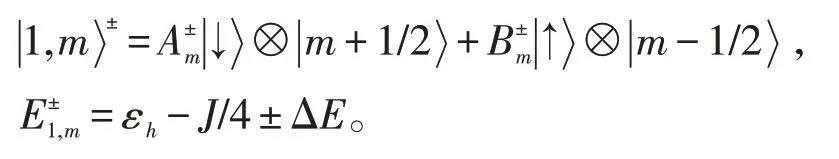
这里

我们把(1)式用Hubbard 算符形式[13-15]表示出来其中那么HT和HASMM就可以写成
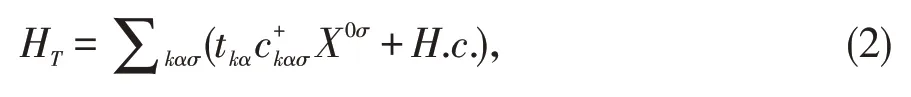

其中,

接下来,我们计算电导[16],根据电流的表达式:

和电导定义:

其中,fα=L,R(ω)=1/[1+expβ(ω-μα)]是电子的费米分布函数,μL=v表示电偏压,μL=0,Tα(ω)= -Γ是隧穿函数。是推迟格林函数的傅里叶变换式。那么相应的,在 Hubbard 算符表象下就为

其中,δσ=±1(σ=↑,↓), 统计平均值P0m=

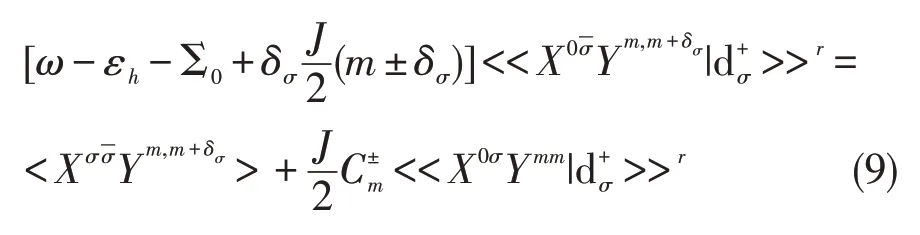

在这里,
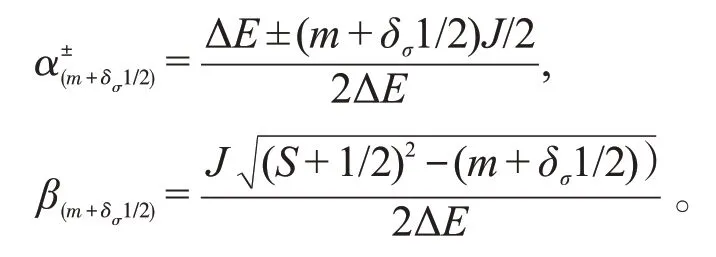
把(10)式带入推迟格林函数中,即得到

在弱耦合近似下:
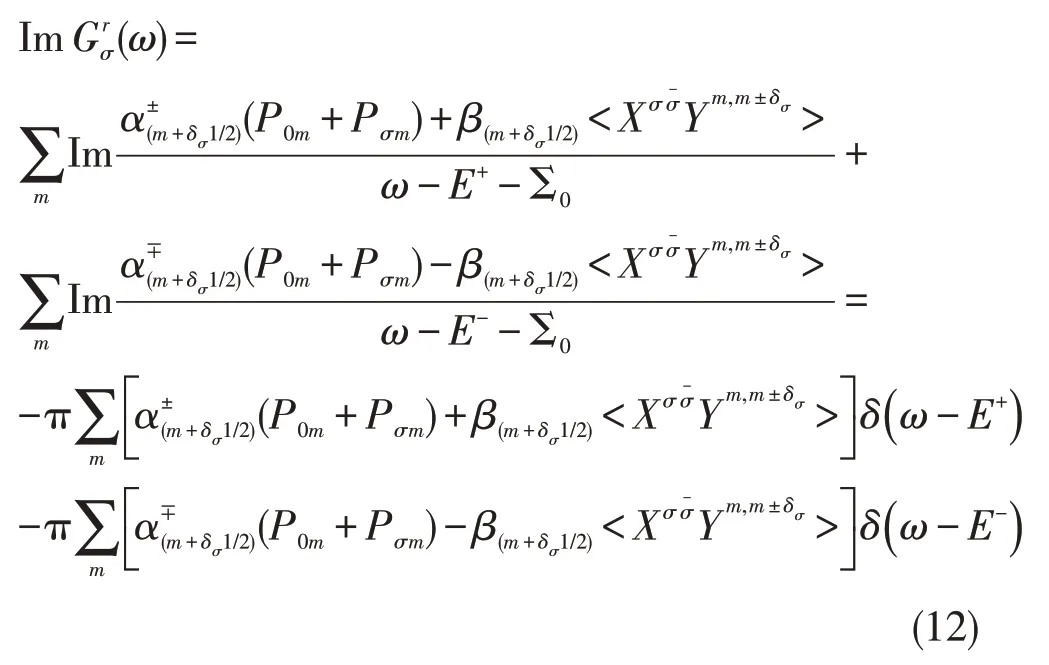
把(12)式代入(6)式中,得到

2 数值分析

图1 S=1/2时的本征态占据几率和线性电导随门电压的变化图

图2 S=1时的本征态占据几率和线性电导随门电压的变化图
图1和图2分别给出S=1/2 和S=1时人工分子磁体顺序隧穿区本征态的态占据几率和电导随门电压变化的关系图。参数为J=1,T=1/β=0.05。且S=1/2 时,我们从图 1 和 2 中可观察到,当 S=1/2 时,εh>0.8 时,空态占据几率为0.5,即其它态为0。同样的情况在S=1,εh>1 时,空态占据几率为1/3,其余态为0,由此数据可说明此时的分子磁体上并没有空穴占据。而在图1 中εh=0.8 和图2 中εh=1 的左侧可 见 ,说明分子磁体上有空穴占据。且在图1中,当εh=0.8,和在图2中,εh=1 的位置上分别出现了一个共振隧穿峰,这里对应着空态和单占据态之间的输运。
3 结论
本文借助电导和电流,电流和格林函数之间的关系,推导出各向同性分子磁体的电导特性,在共振隧穿峰的左右侧,空穴占据情况完全不同,且占据几率受各能级下本征态的个数影响。同时也观察到了空态和单占据态之间的输运情况。
