Numerical investigations of fully nonlinear water waves generated by moving bottom topography

Mian Wang

a Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

b School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Keywords:Underwater landslide Surface gravity waves Euler equations

A B S T R A C T This paper is concerned with propagation of water waves induced by moving bodies with uniform velocity on the bottom of a channel, a simple model for prescribed underwater landslides. The fluid is assumed to be inviscid and incompressible, and the flow, irrotational. We apply this model to a variety of test problems, and particular attention is paid to long-time dynamics of waves induced by two landslide bodies moving with the same speed. We focus on the transcritical regime where the linear theory fails to depict the wave phenomena even in the qualitative sense since it predicts an infinite growth in amplitude. In order to resolve this problem, weakly nonlinear theory or direct numerical simulations for the fully nonlinear equations is required. Comparing results of the linear full-dispersion theory, the linear shallow water equations, the forced Korteweg-de Vries model, and the full Euler equations, we show that water waves generated by prescribed underwater landslides are characterized by the Froude number, sizes of landslide bodies and distance between them. Particularly, in the transcritical regime, the second body plays a key role in controlling the criticality for equal landslide bodies, while for unequal body heights, the higher one controls the criticality. The results obtained in the current paper complement numerical studies based on the forced Korteweg-de Vries equation and the nonlinear shallow water equations by Grimshaw and Maleewong (J. Fluid Mech. 2015, 2016).

Analytical solutions for linear water waves induced by prescribed underwater landslides were thoroughly investigated by Lo and Liu [1]. Three-wave structure was derived in the linear shallow water equations (LSWE) and the linear full-dispersion model (LFD) [1, 2]. By solving the LSWE, Tinti et al. [3] showed that the free-surface displacement y =ζ(x,t) generated by a rigid landslide moving at a constant speed can be given as

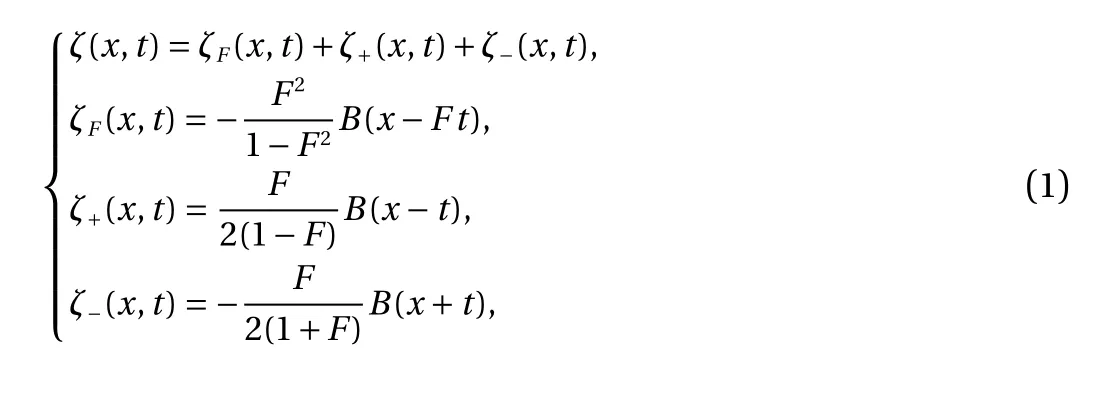
where B (x,t)=B(x-F t) is the locally confined landslide forcing function and F is called the Froude number, a dimensionless parameter defined as the ratio of the uniform speed of landslide bodies to the critical speed of shallow water waves. As for the LFD, wave profiles can be expressed as

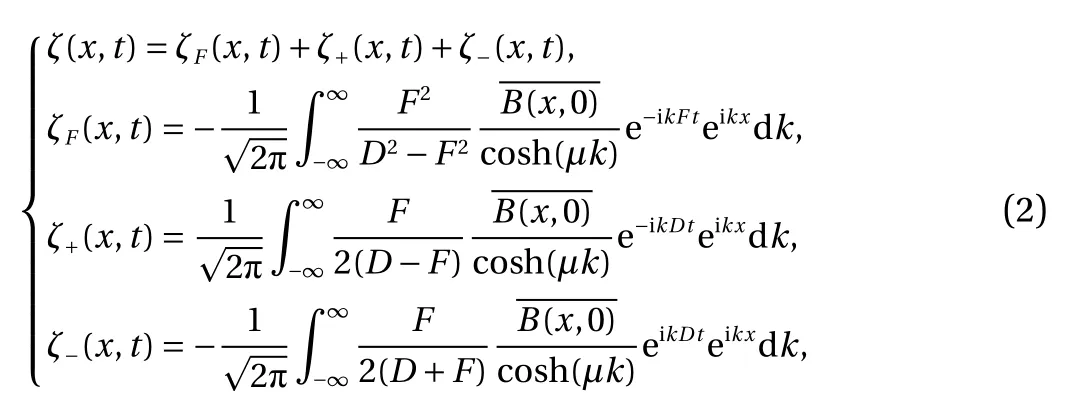
In a frame of reference moving with landslide bodies, the original problem can also be viewed as flow over fixed obstacles on the bottom. For fluid flow over a single localized obstacle, it is well-known that wave behaviors can be classified by the Froude number of upstream water. For supercritical flows ( F ＞ 1), there are downstream waves and the free-surface profile is a local elevation right above the obstacle; while for subcritical flows( F ＜ 1), there are both upstream and downstream waves, and the profile features a local depression at the position of the obstacle.Fundamental wave phenomena in the subcritical and supercritical regimes can be qualitatively understood via the linear theory, and the interested reader is referred to the monograph [4]and references therein.

However, the linear theory fails in the transcritical regime( F ≈ 1) since it predicts unlimited growth of wave amplitude owing to the non-dispersive nature at wavenumber k =0 (i.e. the long-wave approximation), and then it is necessary to invoke the nonlinear effect as the amplitude reaches a certain level. As pointed out by Grimshaw and Maleewong [5], the nonlinear and non-dispersive shallow water theory leads to a locally steady hydraulic flow over the obstacle, with upstream- and downstreampropagating shocks to interrupt the increase of amplitude. In the presence of weak dispersion, the forced Korteweg-de Vries equation (fKdV) was invoked to describe this flow in the weakly nonlinear regime, where shocks are resolved by undular bores[6]. The fKdV was initially proposed by Akylas [7] to explain the periodic shedding of upstream advancing solitons by a moving surface pressure, which eventually turns into an undular bore for the long-time dynamics, a phenomenon first observed numerically by Wu and Wu [8]. In the transcritical regime nonlinear wave generation by bottom topography and by surface pressure forcing share the same weakly nonlinear model, and the formation of soliton and undular bore attributes to the subtle balance between weak dispersion and weak nonlinearity.

Based on the full Euler equations, the dependence of flow behavior on obstacle shape and size was also investigated by various authors. Forbes and Schwartz [9] computed steady solutions for fluid flow over a semi-circular obstruction and showed that for F ＜1 an essentially wave-free region is obtained upstream followed by a train of nonlinear Stokes waves downstream, and a symmetric solitary-like wave can be found for F ＞1. In the nearly critical regime, hydraulic falls were calculated by Forbes [10], who found that as the radius of the submerged obstacle is increased, the speed of the downstream portion of the flow increases, with a consequent reduction in the upstream Froude number. For a submerged triangular obstacle,Dias and Vanden-Broeck [11] studied waves of permanent form without oscillation in the far field, and they found that solutions exist for triangles of arbitrary size. For transcritical flows past a step, Grimshaw et al. [12] showed numerically and asymptotically that a positive step generates an upstream-propagating undular bore formed by an elevation upstream of the step, while a negative step generates a downstream-propagating undular bore formed by a depression downstream of the step.

When the landslide is composed of two well-separated bodies or when one landslide body breaks up into two parts, the landslide-induced surface waves become more complicated,and the corresponding mechanisms need to be elucidated.Based on the weakly nonlinear theory (fKdV) and laboratory experiments, Pratt [13] pointed out that the formation of a train of waves "trapped" between two obstacles is needed to obtain a stable solution. Later on, Dias and Vanden-Broeck [14] numerically found similar trapped-wave solutions in the steady Euler equations. Binder et al. [15] considered the same problem, and new solutions complementing those of were found [11]. Chardard et al. [16] examined the stability of trapped-wave solutions in the fKdV, which were found to be unstable. Based on the nonlinear shallow water equations, Grimshaw and Maleewong [5]showed that initially there are one upstream elevation shock and one downstream depression shock generated at each obstacle and as time involves the shock interaction occurs between two obstacles. The interaction is determined by the second one for equal obstacles, while the higher one controls criticality for unequal obstacle heights. In the subsequent research, Grimshaw and Maleewong [17] used the fKdV to take into account the dispersive effect, which results in the formation of undular bores instead of shocks. Though this problem was thoroughly investigated via weakly nonlinear models, the results have not been verified with the full Euler equations, which is the main task of the present paper.

The primary purpose of this paper is to compare the linear theory, the fKdV model with the full Euler equations for flows over two well-separated obstacles, which extends the previous work by Lo and Liu [1] and Grimshaw and Maleewong [5, 17].The fully nonlinear equations are numerically solved using the time-dependent conformal mapping, a technique pioneered by Ovsjannikov [18]. Then we give the mathematical description of the full problem, and reformulate the potential theory equations in the conformally mapped domain. The numerical results are presented, and particular attention is paid to the long-time behavior of the fully nonlinear equations and how the characteristic scales of landslide bodies impact on water waves. The concluding remarks are given in the end.

In reality, underwater landslide body is of a deformable shape as it interacts with fluid motion, and it moves at a changeable speed which is quite difficult to be captured in time. As done in Ref. [1], we make two basic assumptions to simplify the problem: the movement of the landslide body is modelled as a time-dependent bottom topography translating horizontally without changing its shape (i.e. rigid body approximation) and the relative speed between the landslide body and water flow is assumed to be constant. The fluid is assumed to be inviscid and incompressible, and the flow, irrotational. We introduce a new frame of reference moving with the landslide body, therefore the original problem is transformed to free-surface flows over submerged obstacles, and a sketch of the model is shown in Fig. 1.

We introduce Cartesian coordinates with the x -axis along undisturbed free surface and the y -axis directed vertically opposite to gravity. Let the bottom topography denoted by y=-H+b(x), where b (x) is a function with compact support modeling the locally confined landslide body. In the far field, the upstream flow is characterized by a constant depth H and a constant horizontal velocity U. Henceforth, we non-dimensionalize the system by choosing a length scale H, a velocity scaleand a time scale of, in terms of which the governing equations read

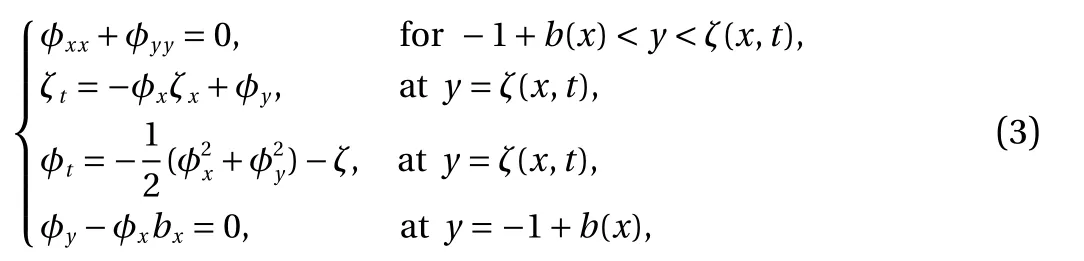
where ζ (x,t) is the free surface elevation, φ (x,y,t) the velocity potential, and g the acceleration due to gravity. The fluid density is assumed to be unitary without loss of generality, and also,non-dimensional units in which the acceleration of gravity and a characteristic depth scale are equal to one can be understood.

To solve the free-surface Euler system Eq. (3), the time-dependent conformal mapping formulation is adopted. This technique was first introduced by Ovsjannikov [18] and developed by Dyachenko et al. [19], and subsequently developed and used by many researchers in the water-wave community for different problems (see Refs. [20-26] for example). To formulate the freesurface system Eq. (3) in the conformal space, the first step is to find an analytic transformation z =x(ξ,η,t)+iy(ξ,η,t) that maps the physical domain filled by fluid into a strip of uniform thickness h ＞0, where h is time-dependent and will be determined later. This is achieved by solving the Laplace equation

where the free-surface displacement and the known bottom topography provide boundary conditions. Then the harmonic conjugate x (ξ,η,t) is determined through the Cauchy-Riemann relations

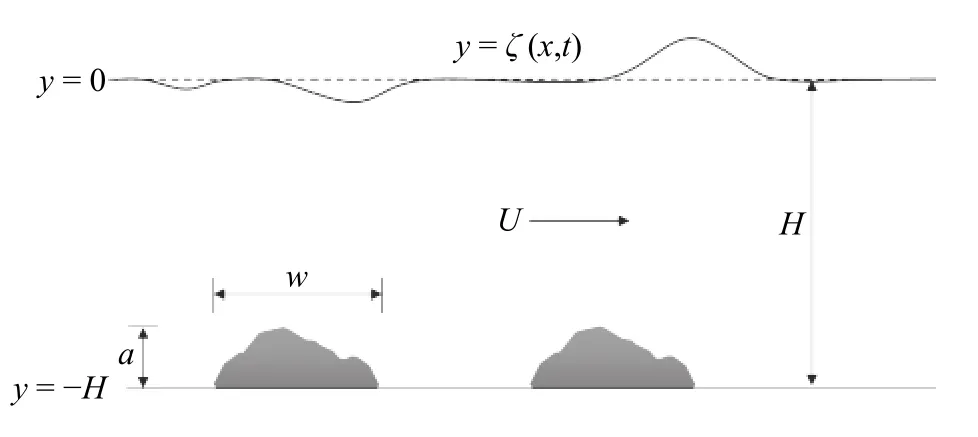
Fig. 1. Sketch of the landslide-induced wave problem

where C and S are linear operators with Fourier symbols defined as=icoth(nk0h) and=i/sinh(nk0h), respectively. The velocity potential, φ, and the streamfunction, ψ , also form a harmonic-conjugate pair. Therefore in the same vein, we can obtain the relation betweenandas

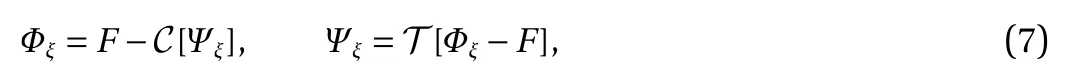
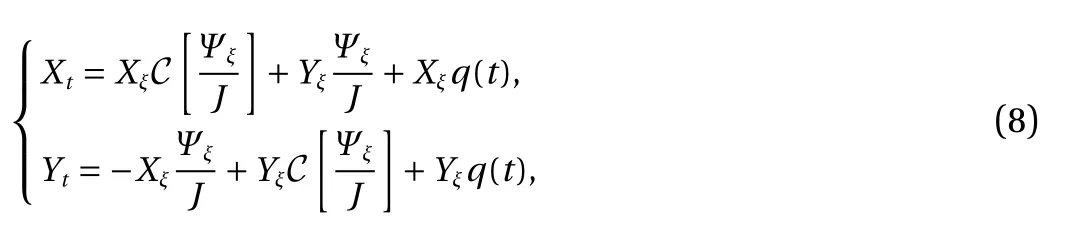
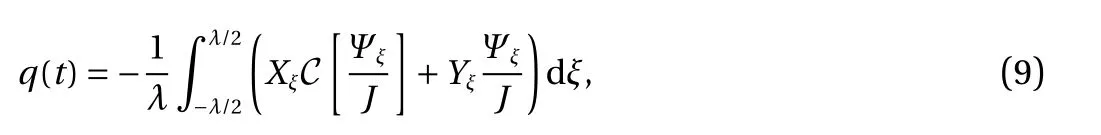
so that x0(t) is independent of time. Finally, the dynamic boundary condition in the transformed plane can be rewritten as

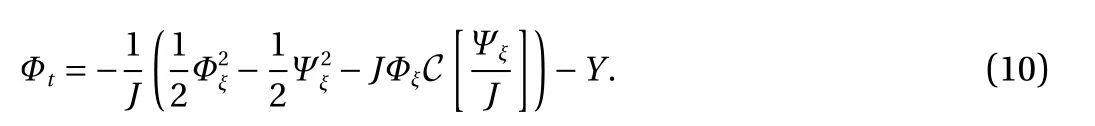
Equations (8) and (10) form a complete system for the unknown functions Y and Φ. Periodic boundary conditions are used at endpoints of the computational domain. Therefore the pseudospectral method can be adopted to solve the obtained system.The computational domain is set to be sufficiently long, and in all figures demonstrated only the part of the domain, containing wave activity, is shown. The pseudo-differential operators C and S, together with all derivatives, can be efficiently computed in the Fourier space using Fourier multipliers, and nonlinear terms are solved in the physical space. Finally, the classical fourthorder Runge-Kutta method is used for time evolution.

In this section, we present results obtained using the numerical method described. The landslide bodies on the bottom of the channel are given as two Gaussian profiles, namely,

where the height and width are defined respectively by aiand wifor i =1,2. The distance between two bodies is defined as|x1-x2|.

In the case of flows over a single obstruction, we set x1=a2=0 , a1=0.05 and w1=50. The numerical results are compared with theoretical solution, the fully nonlinear equations(FNE), and fKdV which is given by

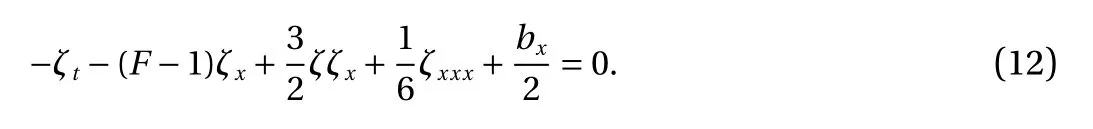
In the subsequent analyses, we focus on numerical solutions of the fKdV and the FNE. As pointed out by Grimshaw and Maleewong [17], in the weakly nonlinear theory the limiting range of the transcritical regime reads

Moreover, for a single obstacle the wave amplitude can be predicted as

where ζ-represents the downstream amplitude while ζ+stands for the upstream amplitude. Another two key features are the amplitude of the leading wave upstream Aw-and the amplitude of the leading wave downstream Aw+. As pointed out by Grimshaw et al. [12], Aw-=2ζ-and Aw+=-2ζ-in the fKdV theory. A quantitative comparison is made in Table 1, where a good agreement is found between the theoretical prediction and numerical results for the full Euler equations. Furthermore, by varying characteristic sizes of the landslide body, it is found that there is a positive correlation between wave amplitude and obstacle height. Comparing the results of different widths, we found that for ω1＜50, the amplitude of upstream-advancing solitary waves increases and then decreases when ω1is slightly greater than 50 at exact criticality (i.e. F = 1 ).

In the transcritical regime, nonlinear waves can be generated both upstream and downstream for a uniform flow over a single localized obstacle, as a consequence wave interactions may occur in the presence of two well-separated obstacles. It is of interest to study long-time behaviors of landslide-generated waves in the case when a single landslide body breaks up into two.

Firstly, we consider wave interactions between two equal landslide bodies. Numerical simulations of the FNE (solid line)and the fKdV (dash-dotted line) are showed together for comparison purposes. In Fig. 2, we show results at exact criticality.Initially in the wave generation process there are both upstream and downstream undular bores near each obstacle (see t =80).The upstream undular bores are attached to obstacles while the downstream ones propagate away from obstacles. Therefore the undular bores between two obstacles interact with each other gradually (see t =300). For the long-time dynamics, the results resemble a transcritical flow generated by the first obstacle where there is an attached undular bore upstream, a depression zone connected with an undular bore propagating far downstream, and locally a supercritical flow over the second obstacle.It is noted that there appears a train of solitary waves between two obstacles but they are not stationary. The largest amplitude occurs upstream of landslide bodies, which may give a clue for underwater-landslide detection. In addition, there are also shape-stabilized wave trains propagating downstream whose amplitudes are close to the height of landslide bodies.

Figure 3 shows the case of F =1.2 which is slightly below the superscritical regime (the upper bound for the transcritical regime is F =1.274 due to Eq. (13)). It is found that there are upstream-propagating solitary waves and downstream-propagating undular bores. As time involves, solitary waves move continuously upstream and finally a local supercritical flow occurs above two obstacles. The most striking feature in this case is thenon-existence of waves between two landslide bodies after longterm interactions. In both Figs. 2 and 3, upstream waves spread faster in the fKdV than that in the FNE, while the wave amplitudes in these two models are very similar.

Table 1 A quantitative comparison of the numerical simulations of the fKdV equation and the Euler equations with the theory.() is the amplitude of the leading wave of the upstream(downstream) undular bore.

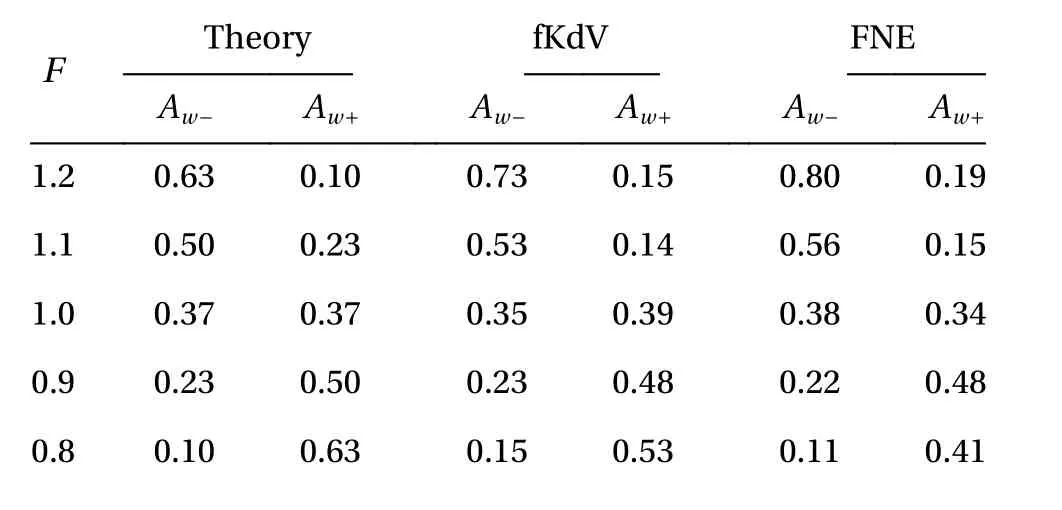
Table 1 A quantitative comparison of the numerical simulations of the fKdV equation and the Euler equations with the theory.() is the amplitude of the leading wave of the upstream(downstream) undular bore.

F Theory fKdV FNE Aw- Aw+ Aw- Aw+ Aw- Aw+1.2 0.63 0.10 0.73 0.15 0.80 0.19 1.1 0.50 0.23 0.53 0.14 0.56 0.15 1.0 0.37 0.37 0.35 0.39 0.38 0.34 0.9 0.23 0.50 0.23 0.48 0.22 0.48 0.8 0.10 0.63 0.15 0.53 0.11 0.41

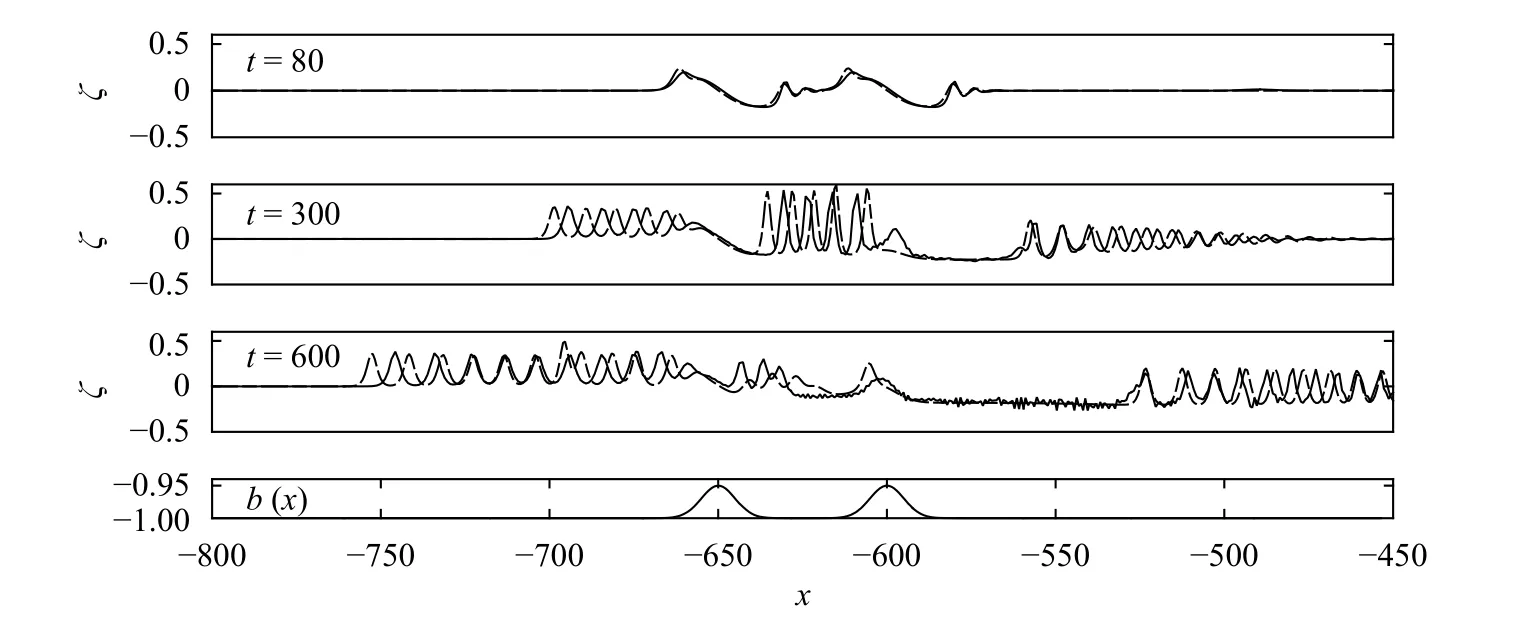
Fig. 2. Snapshots of wave profiles at for, and: the FNE simulation(solid line), the fKdV simulation (dash-dotted line)

Figure 4 is a typical case in the supercritical regime ( F= 1.4),which ultimately shows stationary profiles above obstacles and undular bores propagating downstream. During the wave generation process, there emerges a wave of depression near each landslide body (see the snapshot at t =50), then these oscillations propagate downstream as time involves and almost no waves appear between two bodies. Finally, the flow remains supercritical above two obstacles which has the largest amplitude(approximately twice the height of the landslide body). In this numerical experiment, the amplitude of waves in the FNE is larger than that in the fKdV. It is worth mentioning that in contrast to the fKdV theory, the FNE can capture small solitary waves downstream though they are not shown in the figure. A comparison of Figs. 2-4 indicates that the number of waves between two bodies decreases as the Froude number increases and there is always a local supercritical flow above the second obstacle after a long-term interaction.

The simulation for F =0.75, which is slight above the subcritical regime (the lower bound of the transcritical regime is F=0.726according to Eq. (13) based on the fKdV theory), is shown in Fig. 5. As we can see from the result, undular bores are found to propagate both upstream and downstream, and transient and irregular waves exist in between. Downstream waves in the FNE cover a smaller area than that in the fKdV. Waves with the largest amplitude stay downstream while the magnitude is smaller than the theoretical prediction. The results of long-term dynamics show that the flow stays subcritical above two landslide bodies. In the FNE simulation, the amplitude of upstream waves is approximately of the same magnitude as the landslide body.

Figure 6 shows a typical case in the subcritical regime( F= 0.6). Solitary-like waves can be found to propagate both upstream and downstream in the FNE. The flow stays subcritical over two obstacles and no waves are found in between. Finally,we remark that the fKdV overestimates the amplitude of waves in Fig. 6. Finally, we change the distance between two landslide bodies and find that there is a negative correlation between wave amplitude and the distance between two obstacles.

Next, we carry out numerical experiments to explore the characteristics of waves induced by unequal landslide bodies.Solutions for a1=2a2=0.05 are shown in Figs. 7(a)-11(a), while for a2=2a1=0.05 are shown in Figs. 7(b)-11(b). Due to the fKdV theory, the transcritical regime for ai=0.025 reads F ∈[0.81,1.19].In Figs. 7-11, other parameters are: w1=w2=50, x1=-650,x2=-600.

Fig. 3. Snapshots of wave profiles at for, and: the FNE simulation (solid line), the fKdV simulation (dash-dotted line)

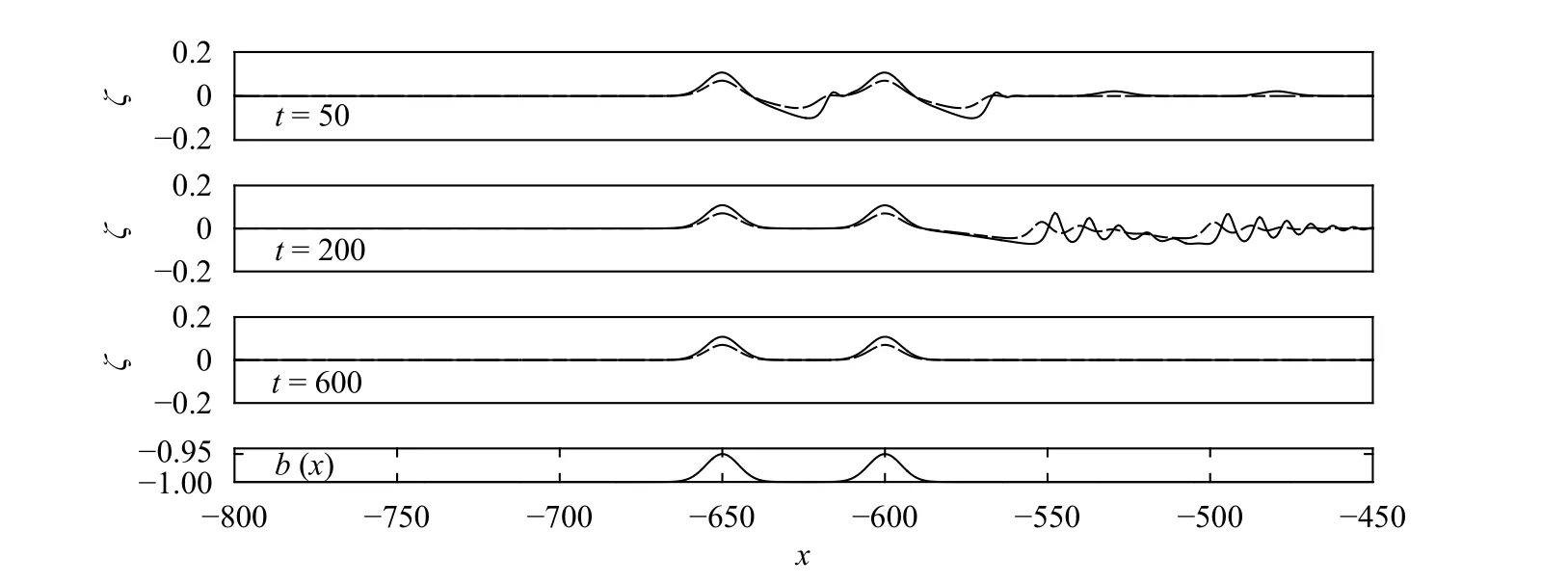
Fig. 4. Snapshots of wave profiles at for: the FNE simulation (solid line), the fKdV simulation (dash-dotted line)

Figure 7 shows the outcome for F =1.0, which is in general similar to that displayed in Fig. 2. When the first obstacle is higher, there exist an upstream undular bore attached to the first obstacle and a downstream undular bore propagates away from the second obstacle, and complicated wave interactions take place in between. While when the first bump is smaller, as shown in Fig. 7(b), the fully developed wave profile resembles a transcritical flow generated by the second obstacle where there is an attached upstream undular bore, a hydraulic fall over the obstacle, and a depressed zone connected with an undular bore propagating downstream. This fact indicates that the second landslide body controls the long-term wave dynamics.

The solution for F =1.2, which is on the boundary between supercritical and transcritical regimes, is shown in Fig. 8, and the phenomenon is qualitatively similar to Fig. 3. In Fig. 8(a), the downstream undular bore covers a smaller range than that in Fig. 3, indicating that the second obstacle controls the wave behavior in the downstream. For waves in Fig. 8(b), it is found that upstream waves move slower while downstream waves move faster than that in Fig. 3. The typical supercritical example is shown in Fig. 9 for F =1.4. Similar to the former case, the downstream undular bore is controlled by the second obstacle in comparison with Fig. 4. Figure 10 demonstrates the solution for F=0.75 at different moments. When the first obstacle is higher,by comparing with Fig. 5, waves between two landslide bodies in the present example have much larger amplitude and the downstream undular bore is shorter. This phenomenon resembles a flow generated by the first landslide body only. In the opposite situation, an interesting phenomenon is observed that in contrast to Fig. 5 there are no waves between two landslide bodies and the downstream undular bore covers a larger area. This case resembles a flow generated by the second landslide body only.Figure 11 shows a typical example in the subcritical regime( F= 0.6). Solitary-like waves are found upstream and their amplitudes show a slow increase before reaching stationary state,which is similar to Fig. 6. The amplitudes of stationary depression profiles over obstacles are strongly influenced by the heights of bottom humps. To sum up, forand w1=w2, the flow is controlled by the landslide body with a greater height in the transcritical regime. However, in the supercritical and subcritical regimes, these two landslide bodies are similarly important. On the other hand, computations of weakly nonlinear and fully nonlinear equations give different upstream spreading velocities of waves in the transcritical regime and different amplitudes in other regimes.

Fig. 5. Snapshots of wave profiles at for: the FNE simulation (solid line), the fKdV simulation (dash-dotted line)

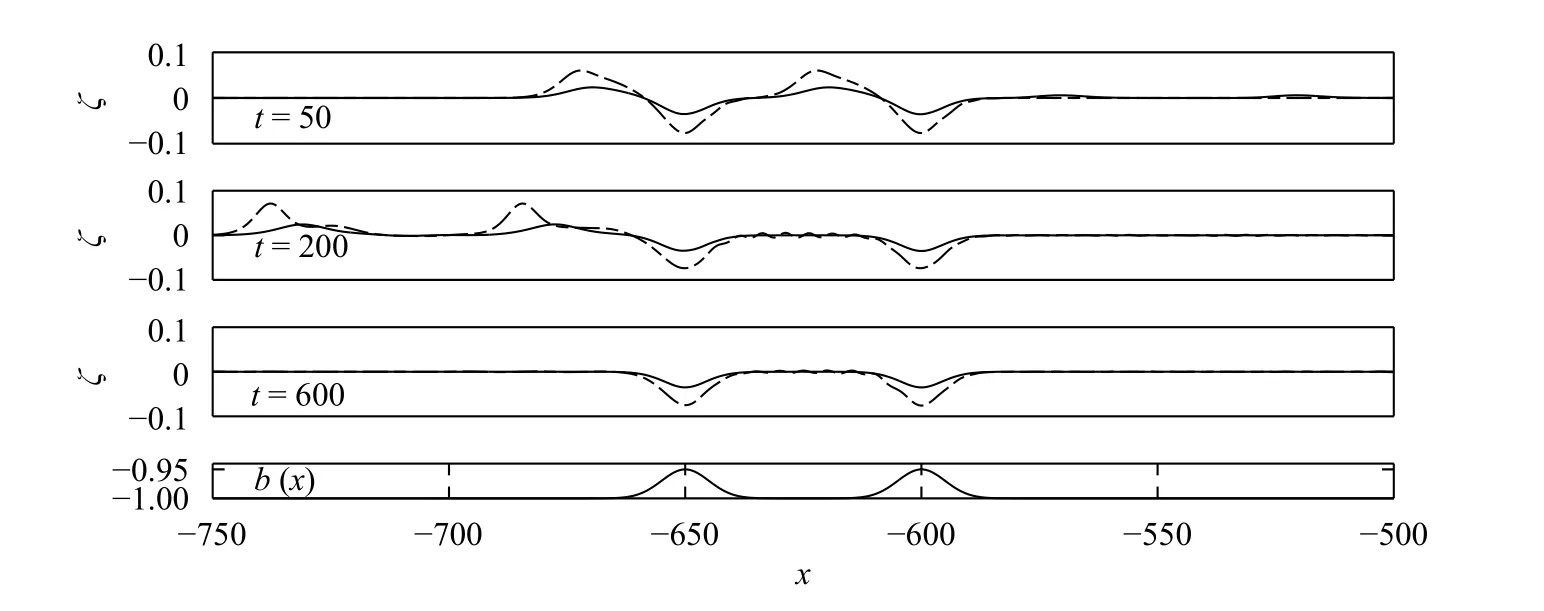
Fig. 6. Snapshots of wave profiles at for: the FNE simulation (solid line), the fKdV simulation (dash-dotted line)

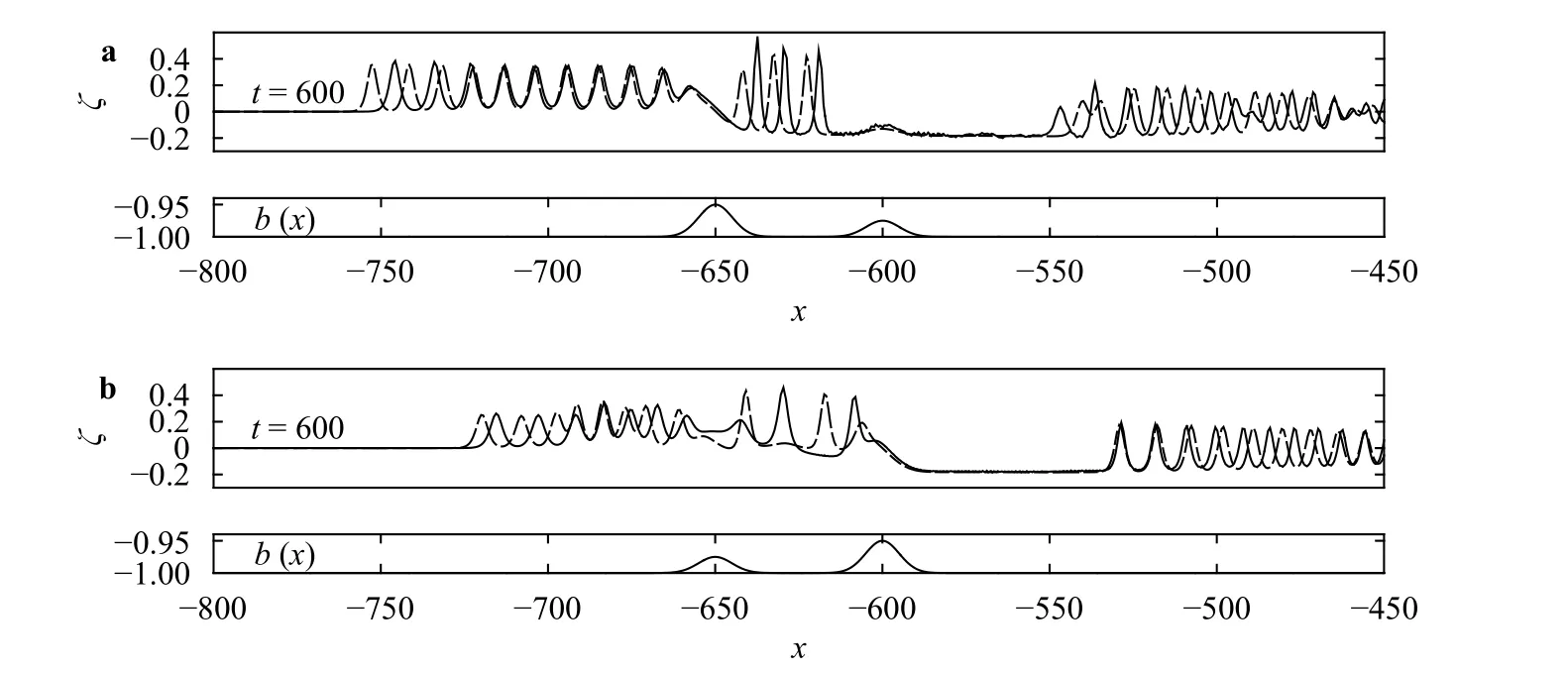
Fig. 7. Snapshots of wave profiles at for: the FNE simulation (solid line), the fKdV simulation (dash-dotted line). a,; b

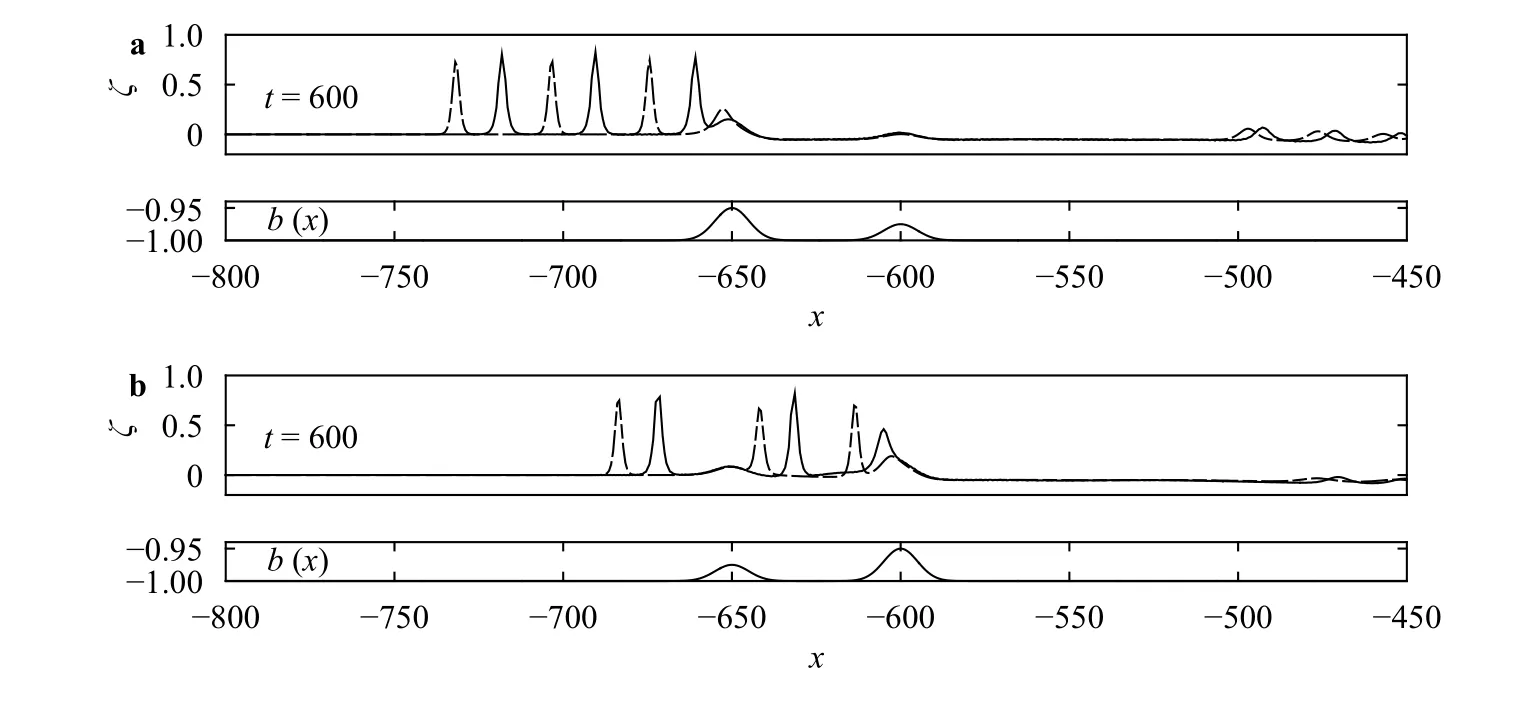
Fig. 8. Snapshots of wave profiles at for : the FNE simulation (solid line), the fKdV simulation (dash-dotted line). a,; b

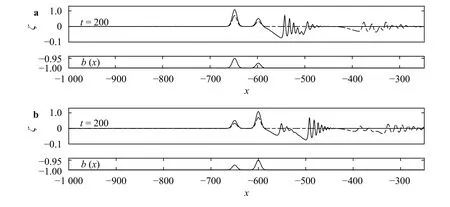
Fig. 9. Snapshots of wave profiles at for: the FNE simulation (solid line), the fKdV simulation (dash-dotted line).a,; b

We next consider the case of two landslide bodies with different widths (namely,). Figure 12(a) shows the simulation at criticality when the first landslide body is much wider than the second one. In the beginning, the amplitudes of waves generated by the second obstacle is larger than the first one, which is in accord with the laws we found in the last section. After a considerably long time, waves between obstacles are all replaced by an undular bore with large amplitude. Figure 12(b) shows the opposite setting and more oscillations appearing between two obstacles is observed. Comparing these two cases, we found that upstream waves cover a broader range in Fig. 12(a) while downstream waves cover a broader range in Fig. 12(b). Furthermore,we conclude that outside the interacting area, the covering range of the waves is related to the position of the thinner obstacle. It is worth mentioning that in the FNE when F =1.2, there are no waves between two obstacles when the first one is wider, while solitary-like waves can be observed in the opposite case (Fig. 13).This is different from the results in the fKdV theory that these waves exist in both situations.

In the current paper, we have explored the underwater landslide induced water waves primarily in the transcritical regime.Using a time-dependent conformal mapping technique, highorder accurate numerical results have been achieved in the full Euler equations. Our results show that for a single prescribed landslide body the generation and propagation of free-surface waves depends on the Froude number and characteristics of the landslide body. Based on the Froude number, open channel flows can be classified in three categories: subcritical, transcritical and supercritical. There are two stages for amplitude evolution in all categories: a rapid increase stage followed by a quasisteady stage, and it takes the longest time for transcritical flows to reach a quasi-steady state. The characteristics of landslide bodies also have a great impact on induced waves: high and thin obstacles can results in large-amplitude waves.

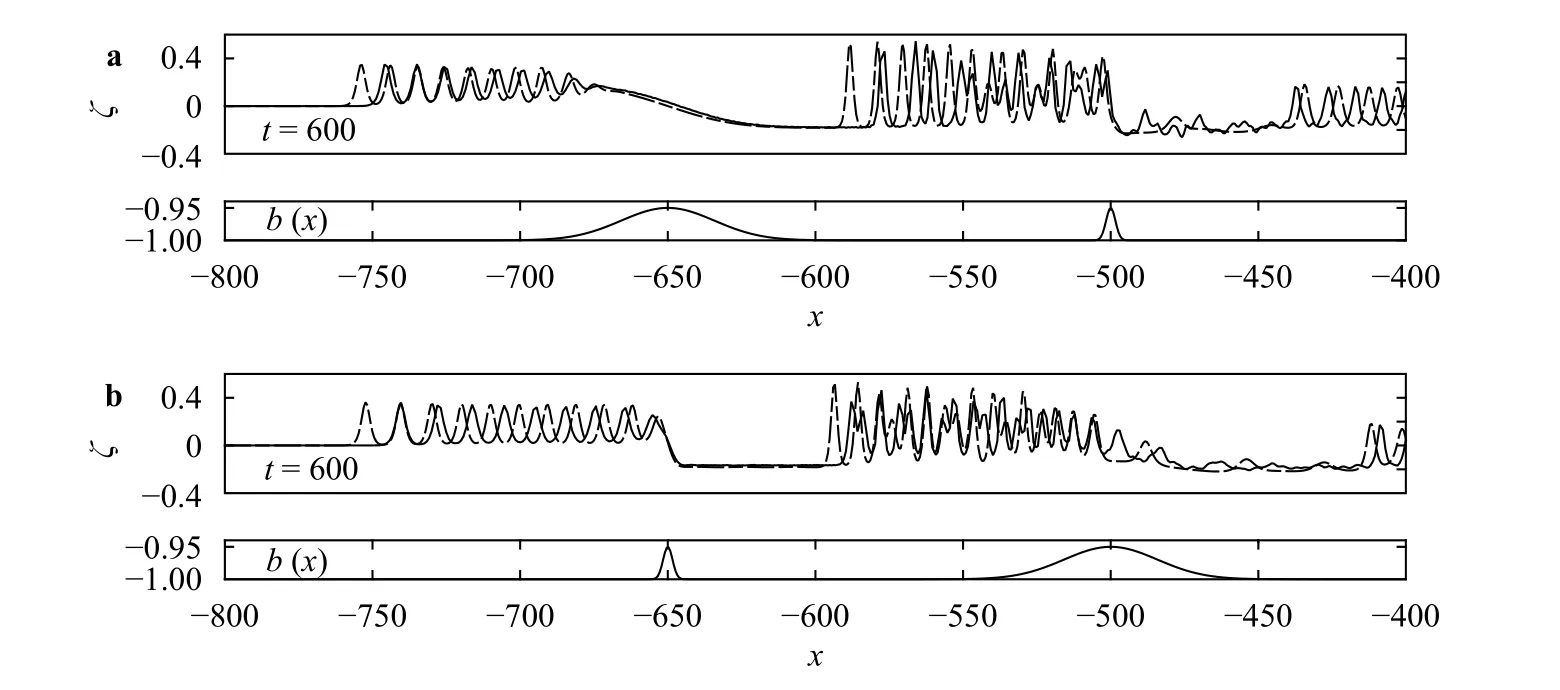
Fig. 12. Snapshots of wave profiles at for: the FNE simulation (solid line), the fKdV simulation (dash-dotted line). a, and ; b , and

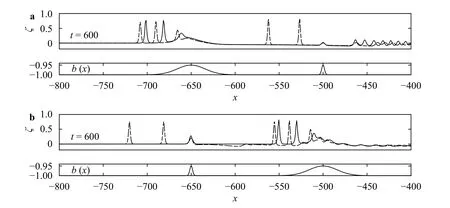
Fig. 13. Snapshots of wave profiles at for: the FNE simulation (solid line), the fKdV simulation (dash-dotted line). a, and; b, and.

We have studied wave interactions between two landslide bodies, which are controlled by the Froude number, relative size and the distance between obstacles. For equal landslide bodies,the second obstacle plays a more important role in controlling the criticality in the transcritical regime and there are largeamplitude solitary waves generated between two obstacles. For supercritical and subcritical regimes, no waves are observed between two bodies and these two obstacles are equally important. When the landslide bodies have different heights, the flow is controlled by the higher one and when the landslide bodies have different widths, the covering range of waves is more related to the thinner one in the transcritical regime. By changing the distance of two bodies, we find that the amplitude decreases as the distance increases.

We have compared the numerical results in the fully nonlinear equations with linear and weakly nonlinear theories. In the transcritical regime where the linear theory fails to describe wave behaviors, it is found that upstream waves spread faster in the fKdV theory than those in the fully nonlinear equations,while amplitudes of waves in these two models agree well. When the flow moves at a higher speed, amplitudes of steady waves in the Euler equations are larger than those in the fKdV, however,the fKdV overestimates wave amplitude in the subcritical regime. Therefore we can conclude that in most cases the linear dispersion plays an important role, but the balance of nonlinearity and dispersion is a key factor near resonance. We remark that in reality a landslide body moves with changeable velocity due to friction and other factors. This time-dependent conformal mapping method can be also used to the case when the shape of landslide body depends on time [27], and the generation and propagation of surface water waves induced by variable-speed landslides will be reported somewhere in the near future. Lastly,along this line, to remove the rigid body assumption and investigate the coupling between free-surface waves and a moving deformable body is a natural and important extension.

Acknowledgement

This work was supported by the Key Research Program of Frontier Sciences, Chinese Academy of Sciences (CAS)(Grant QYZDBSSW-SYS015), and the Strategic Priority Research Program of CAS (Grant XDB22040203). The author would also like to acknowledge the support from CAS Center for Excellence in Complex System Mechanics.