Transient thermal response of functionally graded piezoelectric laminates with an infinite row of parallel cracks normal to the bimaterial interface
2019-11-04YoshiyukiMabuchiSeiUeda
Yoshiyuki Mabuchi, Sei Ueda
Department of Mechanical Engineering, Osaka Institute of Technology, Osaka, Japan
Keywords:Functionally graded piezoelectric material Fracture mechanics Stress intensity factor Elasticity
A B S T R A C T In this paper, the problem of a functionally graded piezoelectric material strip (FGPM strip)containing an infinite row of parallel cracks perpendicular to the interface between the FGPM strip and a homogeneous layer is analyzed under transient thermal loading condition. The crack faces are supposed to be completely insulated. Material properties are assumed to be exponentially dependent on the distance from the interface. Using the Fourier transforms, the electro-thermoelastic problem is reduced to a singular integral equation, which is solved numerically. The stress intensity factors are computed and presented as a function of the normalized time, the nonhomogeneous and geometric parameters.
Recently, several kinds of piezoelectric actuators have been designed. Hall et al. [1] fabricated a mono-morph actuator made from semi-conductive piezoelectric ceramics. Therefore, the elucidation of fracture behavior of piezoelectric systems such as actuators is important. Moreover, the research on transient electro-thermo-elastic problem for functionally graded piezoelectric material (FGPM) laminate with a crack normal to the biomaterial interface has been reported [2].
On the other hand, cracks occur primarily from plural defects in material. The elucidation of interaction between cracks to affect fracture behavior is also important, because these cracks may lead to fracture of material [3].
In this paper, we theoretically analyzed the thermal fracture problem of mono-morph actuators using an FGPM strip with an infinite row of parallel cracks due to an instantaneous temperature change. The analytical laminate model of the mono-morph actuator consists of an FGPM strip and a homogeneous elastic layer. Material properties are exponentially dependent on the distance from the interface between the FGPM strip and the homogeneous elastic layer. Using the Fourier transform technique[4, 5], the electro-thermo-elastic problem is reduced to a singular integral equation, and the Gauss-Jacobi numerical integration formula was used in the numerical analysis of the singular integral equation [6]. The stress intensity factors of the embedded crack are computed and presented as functions of the normalized time for the various values of the nonhomogeneous and geometric parameters.
As shown in Fig. 1, suppose an FGPM strip with the thickness h1containing an infinite row of parallel cracks of equal length 2 c=b-a(0 <a <b <h1) being spaced at equal distance 2dperpendicular to the free boundaries bonded to an elastic layer with the thickness h2. The system of rectangular Cartesian coordinates ( x,y,z) is introduced in the material in such a way that one of the crack is located along the z -axis, and the x-axis is parallel to the boundaries. The FGPM strip is poled in the z-direction and is in the plane strain conditions perpendicular to the yaxis. It is assumed that initially the medium is at the uniform temperature TIand is suddenly subjected to a uniform temperature rise T0H(t) along the boundary z=h1, where H(t) is the Heaviside step function and t denotes time. The temperature along the boundary z =h2is maintained at TI. The crack faces remain thermally and electrically insulated.
The material property parameters are taken to vary continuously along the z-direction inside the FGPM strip. The material properties of FGPM strip, such as the elastic stiffness constants ckl(z), piezoelectric constants ekl(z), dielectric constants εkk(z),stress -temperature coefficients λkk(z), coefficient of heat conduction κx(z), κz(z), and the pyroelectric constant pz(z), are one dimensionally dependent as
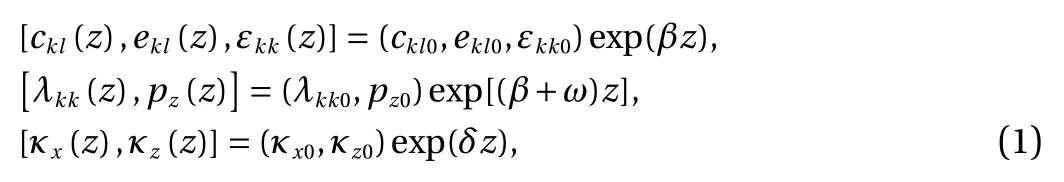
where β, ω, and δ are positive or negative constants, and the subscript 0 indicates the properties at the interface plane z =0.For some materials, the thermal diffusivity τ0indeed does not vary dramatically, then τ0is assumed to be a constant.The material properties of the homogeneous elastic layer are the elastic stiffness constantsstress-temperature coefficientscoefficient of heat conduction κE, and thermal diffusivityThe superscript E denotes the physical quantities of the homogeneous elastic layer.
The crack problem may be solved using the superposition technique. In the problem considered here, since the heat conduction is one dimensional and straight crack does not obstruct the heat flow in this arrangement, determination of the temperature distribution and the resulting thermal stress would be quite straightforward and the related crack problem would be one of mode I. The lines of the centers of the cracksx=±2nd(n=0,1,2,...)are the axes of symmetry of the configuration. We suppose that the crack is opened under the action of same distribution of the internal pressurewhereis the thermal stress induced by the time-dependent temperature change. The thermal stresshas been already obtained in Ref. [2]. In the following, the subscripts x ,y,z will be used to refer to the direction of coordinates.
The governing equations for the electromechanical fields are given in previous paper [2]. The boundary conditions can be written as
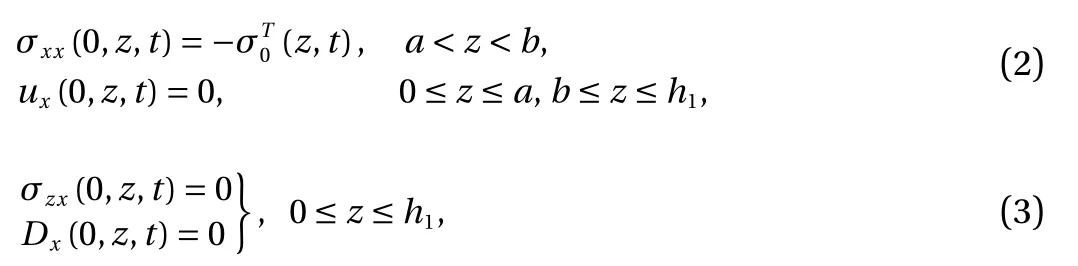

The general solutions of the governing equations for the FGPM strip are obtained by using the Fourier integral transform technique [4]
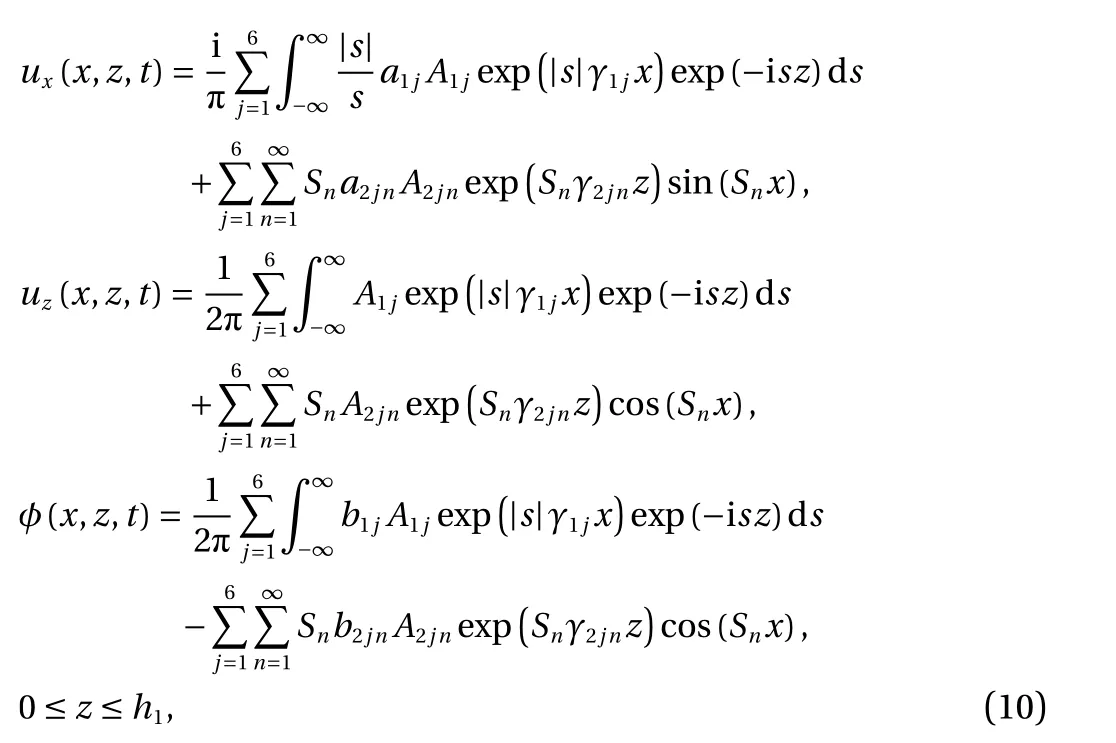
On the other hand, the general solutions of the governing equations for the elastic layer are
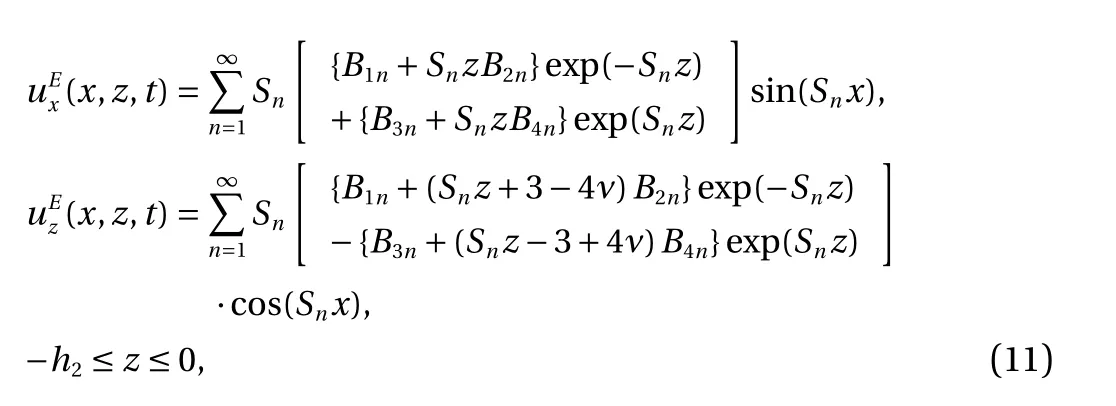
Substituting the displacements and electric potential solutions Eqs. (10) and (11) into the constitutive equations, one can obtain the stresses and electric displacement components.
The stress intensity factors KIAat z =a and KIBat z =b may be evaluated as
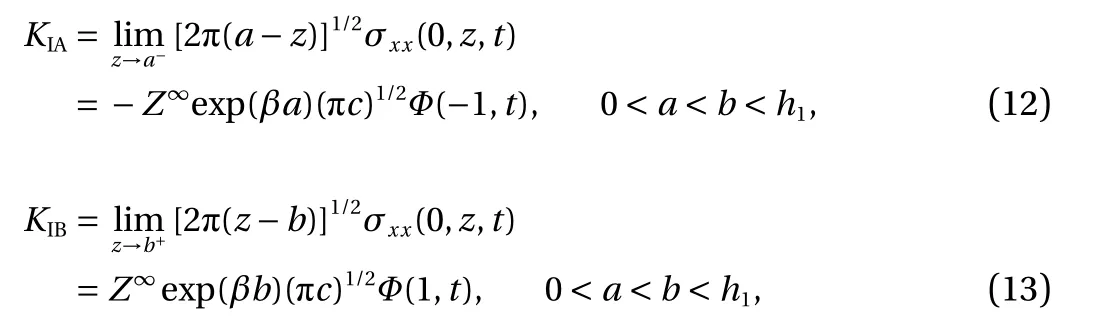
where Z∞is known constant and the function Φ (u,t) are given by

where ξ=(b-a)u/2+(b+a)/2. The function G(ξ,t) is the solution of the following singular integral equation obtained from the boundary conditions Eqs. (2)-(9).
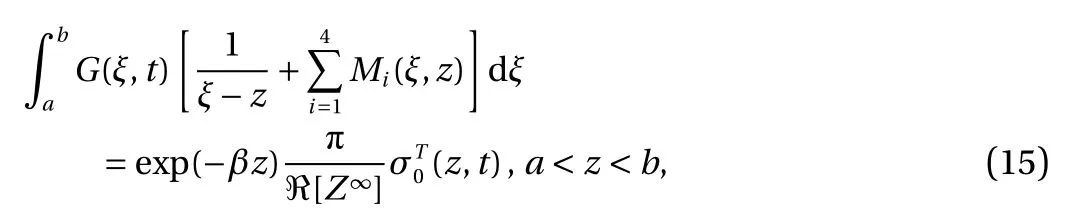
In the integral equation, Mi(ξ,t)(i=1,2,3,4) are known kernel functions obtained by using the boundary conditions.
For the numerical calculations, the properties of cadmium selenide [7] are used as the properties of the FGPM strip at the plane z =0. The normalized nonhomogeneous parameters β h1,ωh1and δ h1are assumed to be β h1=ωh1=δh1. The number of the terms for obtaining the highly accurate values of the infinite series and infinite integral solutions is depends on the geometric parameters. Then all numerical calculations are preformed to keep the relative errors smaller than 1 .0×10-5. We consider the effect of the crack spacing d /h1and the nonhomogeneous parameter β h1on the stress intensity factors KIAand KIBfor the Ti (titanium) elastic layer.[KIA,KIB]/λ110|T0|(πc)1/2versus normalized time F=τ0t/h2for d/h1=0.5, 0 .2 and 0 .1 with c /h1=0.1, h2/h1=1.0,(a+b)/2h1=0.5 and β h1=0.0. Assume the top surface of the strip is heated from initial temperature TIto TI+T0(T0>0) suddenly. Note that the
Figure 2 shows the normalized stress intensity factors values of those intensity factors rise sharply at first, reach maximum values and then decrease and approach the static values with increasing F. Because the change of the thermal stress with Fnear the free boundary is more remarkable than that inside of the FGPM layer [2], the curves of KIBare later to reach stable values than those of KIA. Under heating thermal load, the stress intensity factors decrease monotonically with decreasing d /h1.
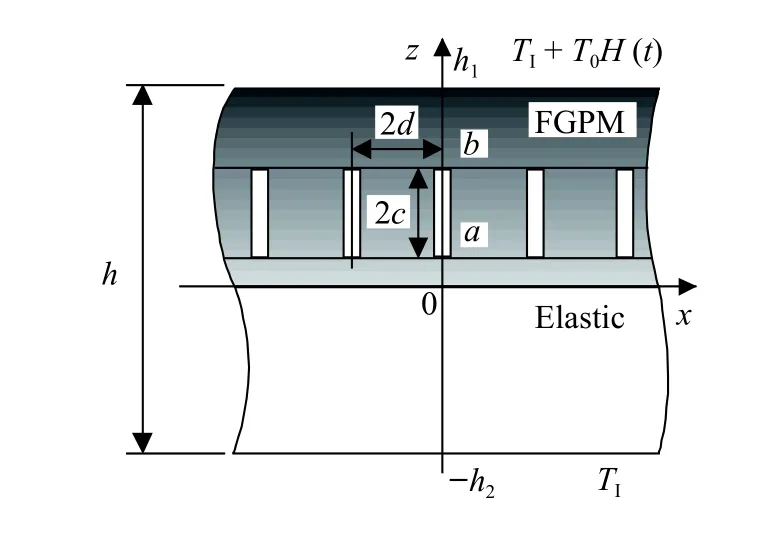
Fig. 1. Geometry of the crack problem in a functionally graded piezoelectric laminate
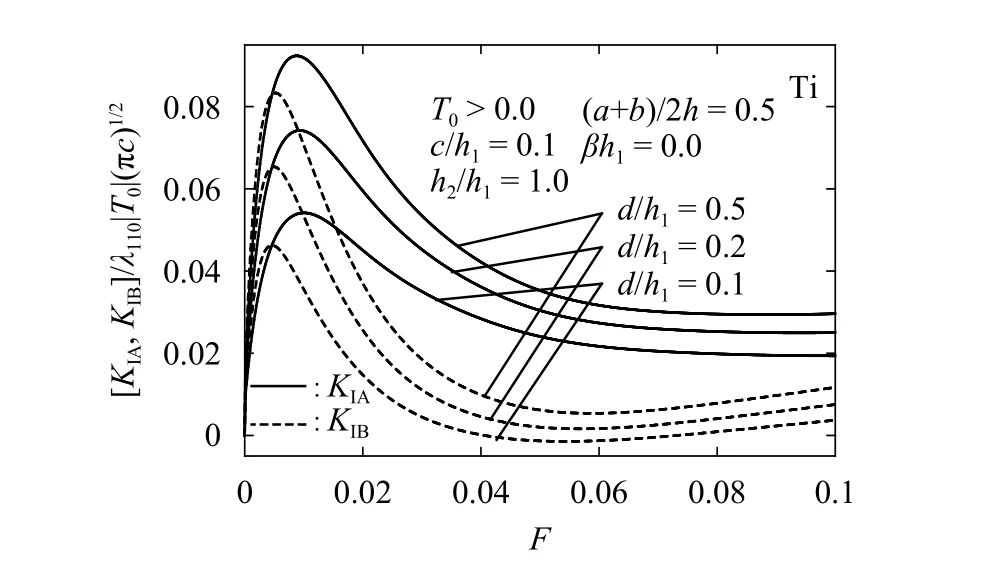
Fig. 2. The effect of the crack spacing on the stress intensity factors and for
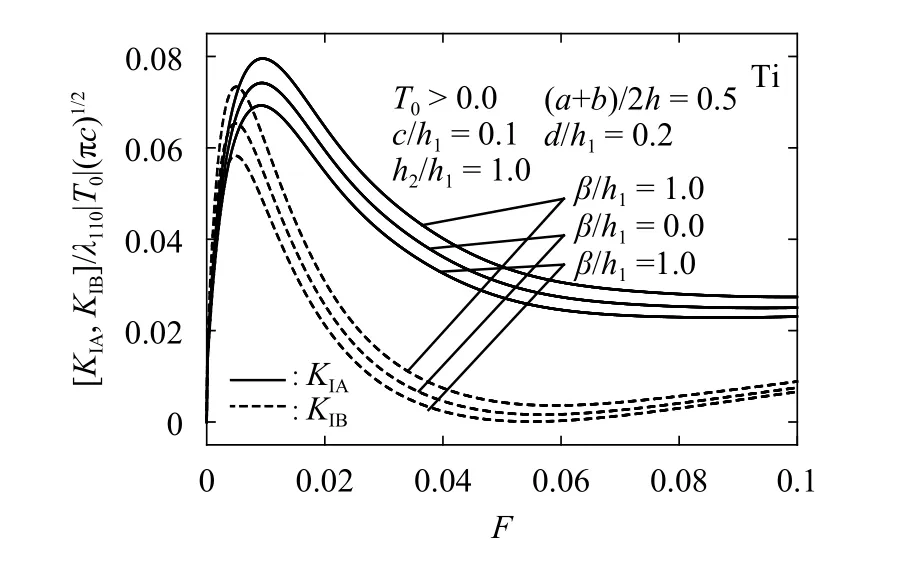
Fig. 3. The effect of the nonhomogeneous parameter on the stress intensity factors and for
Figure 3 shows the effect of β h1on the time dependencies of the normalized stress intensity factors [ KIA,KIB]/λ110|T0|(πc)1/2for βh1=1.0, 0 .0 and - 1.0 with c /h1=0.1, h2/h1=1.0,(a+b)/2h1=0.5 and d /h1=0.2. In this case, the decrease of β h1is beneficial for decreasing the maximum values of the stress intensity factors.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Thermal Stresses
- Stresses of orthotropic laminated beams subjected to high temperature and mechanical load
- Thermoelastic stability of closed cylindrical shell in supersonic gas flow
- Stochastic transient analysis of thermal stresses in solids by explicit timedomain method
- 3D thermally induced analysis of annular plates of functionally graded materials
- Thermoelastic waves in helical strands with Maxwell-Cattaneo heat conduction
