3D thermally induced analysis of annular plates of functionally graded materials
2019-11-04YunFangYangDingChenBoYang
Yun-Fang Yang, Ding Chen, Bo Yang,*
a School of Civil Engineering and Architecture, Zhejiang Guangsha College of Applied Construction Technology, Dongyang 322100, China
b Department of Civil Engineering, Zhejiang Sci-Tech University, Hangzhou 310018, China
Keywords:Annular plate Functionally graded materials Thermo-elasticity Analytical solution
A B S T R A C T
Functionally gradient materials (FGM) is a new kind of heterogeneous composite material. The interface crack and failure can be avoided by controlling the volume distribution of its components along certain direction, which may be prone to occur in traditional composites [1]. The thermoelastic problem is a classical problem in elasticity [2]. Among existing research work related to FGM plates, the thermal analysis of functionally graded plates have been reported. For instance, Cheng and Betra [3]studied the asymptotic solution of the bending problem of isotropic functionally gradient elliptic plates with fixed support under mechanical and thermal loads based on the three-dimensional elastic theory. Based on the unified generalized thermoelasticity theory, Nikolarakis and Theotokoglou [4] studied the thermal shock of three-layer functionally gradient zirconia/titanium alloy slats by using the finite element method.Li et al. [5] obtain the axisymmetric analytical solutions of functionally graded circular plate of transversely isotropic material using direct displacement method.
In the previous research work [6], the authors extended the FGM plate theory established by Mian and Spencer [7] and obtain the analytical solutions of FGM annular plate subjected to mechanical loads. In this paper, the thermal response of functionally graded annular plates is studied based on the generalized Mian and Spencer plate theory.
Figure 1 shows an axisymmetric bending problem of an FGM annular plate with height h, inner radius b, outer radius a,defined in the cylindrical coordinates (r, θ, z). The top and bottom surfaces of the plate are subjected to temperatures T1and T2, respectively. The annular plate turns to be a circular plate as the inner radius b approaches to zero. Denote urand w as the displacement components in the r- and z-directions, respectively; σr, σθ, σzand τrzas the stress components; εr, εθ, εzand γrzthe strain components.
Neglecting body forces, the equations of equilibrium are
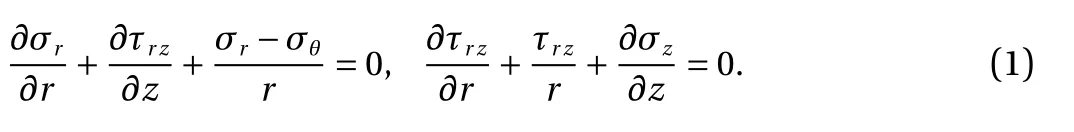
The stress-strain equations for a transversely isotropic material can be given by

in which cijare elastic constants and 2 c55=c11-c12, αiare the coefficients of linear thermal expansion, and T the temperature change from the stress-free state. For a functionally material,these parameters are the functions of thickness coordinate z, i.e.cij=cij(z), αi=αi(z), and T =T(z). By setting c11=c33, c12=c13and α1=α3, the material can reduce from transversely isotropic to isotropic.
According to the generalized Mian and Spencer plate theory[6], the following displacement field is used
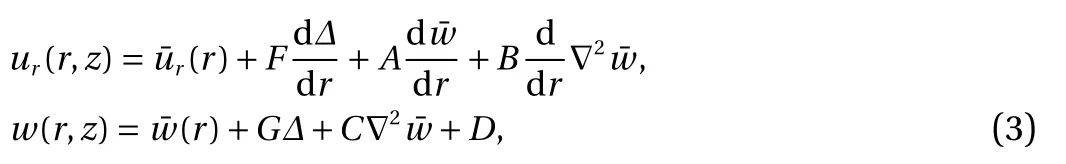
where
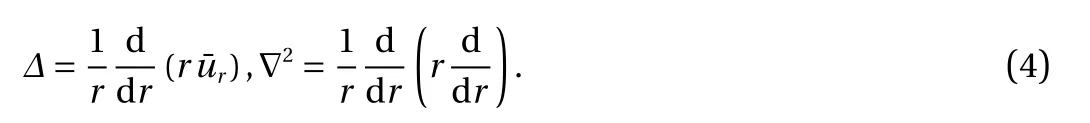
and A ,B,C,D,F , and G are functions of z.
Substituting Eq. (3) into Eq. (2) gives
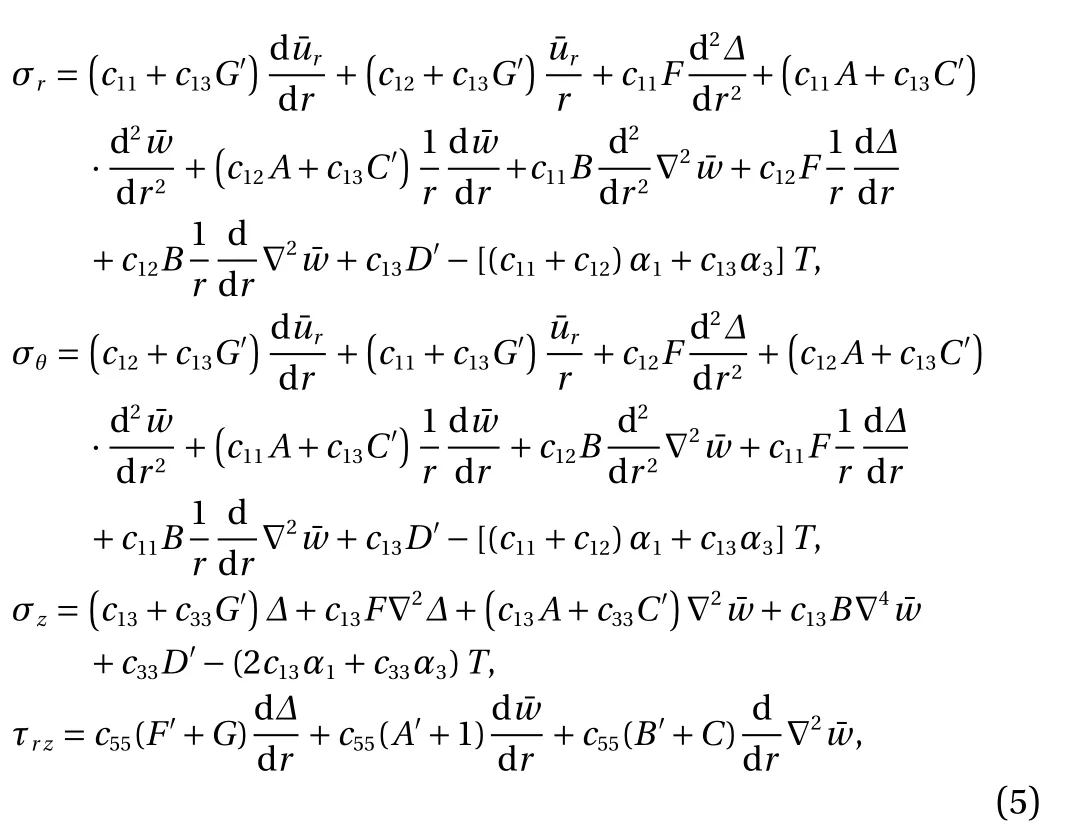
where a prime denotes derivative with respect to z.
By substituting Eq. (5) into Eq. (1), we can obtain
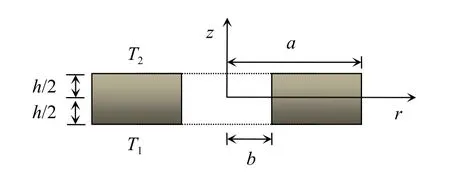
Fig. 1. Diagram of FGM annular plate
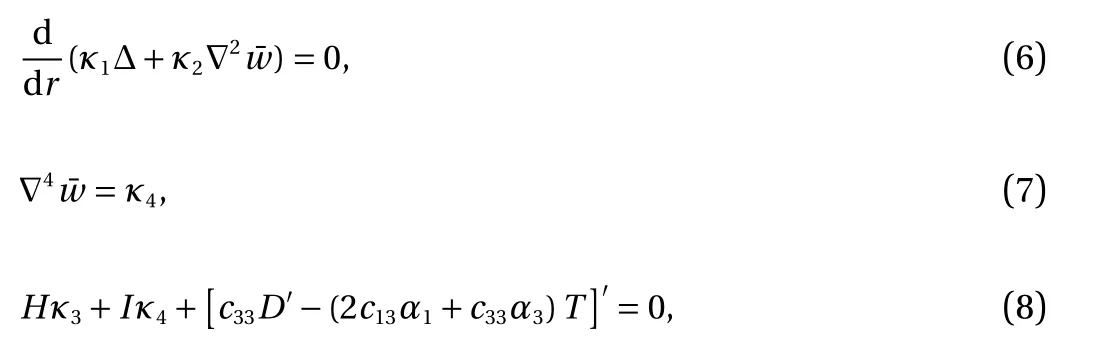
where κ1, κ2, κ3and κ4are arbitrary constants, and
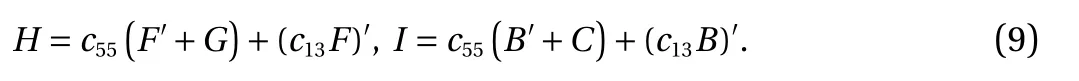
It is noted that Eqs. (6) and (7) are the governing equations for functionsand. Integrating them leads to
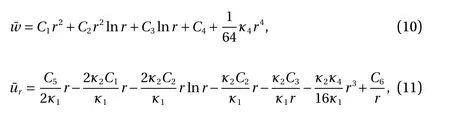
where Ci(i=1,2,...,6) are integral constants which can be completely determined from the cylindrical boundary conditions of the plate.
In this paper, the plate is supposed to be in a steady state and temperature field T (z) varies along the thickness direction. The cylindrical boundaries at r =a and r =b are assumed to be adiabatic. According to Fourier law of heat conduction, the thermal flux qzcan be expressed by

where k=k(z) is the thermal conductivity coefficient. The temperature field T(z) can be governed by the following equation

Integrating Eq. (13) in the thickness direction of the plate yields

where ζ1and ζ2are integral constants which can be determined by the thermal conditions on the top and bottom surfaces of the plate. In this study, some certain temperatures are given at z=±h/2, namely

where T1and T2are known constants.
It can be obtained from Eqs. (14) and (15) that
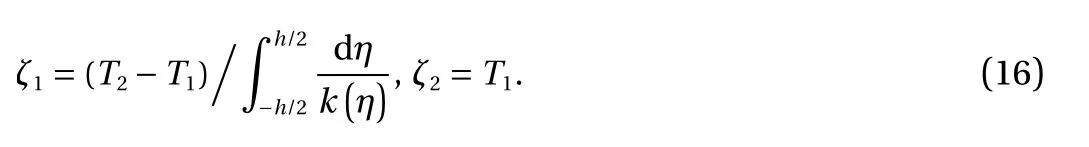
The unknown functions A (z), B (z), C (z), D (z), F (z) andG(z)will be determined by using the stress conditions on the top and bottom surfaces of plate. Assume no mechanical loads are applied on the bottom and top surfaces of the plate, hence we have σz=0, τrz=0 at z =±h/2. Letandto be the mid-plane displacements, we can then obtain the expressions of the functions A(z), B (z), C (z), D (z), F (z) and G (z) [6].
For a functionally graded annular plate, the inner edge( r= b ) and outer edge ( r= a) may be simply-supported (S),clamped (C), or free (F), which requires
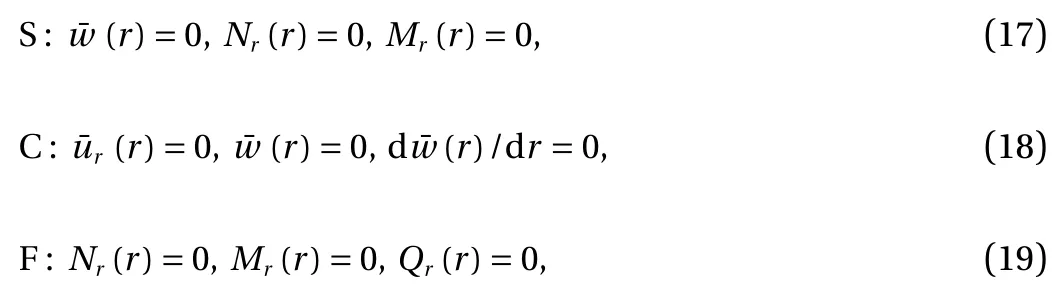
where Nr(r), Mr(r) and Qr(r) are the radial resultant force,bending moment and shear force, respectively [6].
These boundary conditions Eqs. (17)-(19) are sufficient to determine the unknown constants Ci(i=1,2,...,6) in annular plates. The displacements and stress components at any point in the plate can be completely obtained from Eqs. (3) and (5), respectively.
In order to validate the present analysis, a simply supported FGM circular plate subjected to a temperature field is first considered. Our analytical solutions are compared with those reported by Li et al. [5]. The material properties P (z) such as cij, αiand kare graded along the thickness direction according to an exponential function

where P0denotes the material property value at z =-h/2 given in Table 1, and λ is the gradient index characterizing the material inhomogeneity. As a special case, λ =0 corresponds to the homogeneous material.
In this example, the thickness to radius ratio h/a = 0.3, the ratio between the temperatures prescribed on the upper and bottom surfaces T2/T1=15. Table 2 shows the dimensionless deflection W =(w/h)×103at r =0 m. As can be seen that the present solutions not only agree very well with the analytical results but also are closer to the finite element method (FEM) results which are both given by Li et al. [5].
A parametric study is then carried out to investigate the influences of gradient distribution and boundary conditions on the deformation and stress fields of the plate.
Unless stated otherwise, we take T1=10 K, T2=150 K, a =1 m,b=0.1 m, h =0.1 m, and r= (a+b)/2. Meanwhile, the two dimensionless quantities are adopted: w*=w/h×103,=σr/
Figures 2 and 3 display the dimensionless deflection w*and radial stressof the simply supported annular plates under temperature field with different gradient distributions. It is found that the dimensionless displacements are all positive, and increase with the gradient index. It can be seen from Eq. (20)that the material properties, including coefficients of thermal expansion, increase with the gradient index. Hence it is easy to understand why the dimensionless displacements increase with the gradient index. The dimensionless radial stress along the thickness direction is nonlinearly distributed in which the top surface have compressive stresses and the bottom surface have tensile stresses. When the gradient index is greater than zero, the dimensionless radial stress changes more violently.
Figures 4 and 5 illustrate the dimensionless deflection w*and radial stressof the clamped supported annular plates under thermal load with different gradient distribution. The dimensionless displacement on the top surface of the annular plate is positive, and the bottom surface is negative. The mid-plane dis-placement of the center point of the annular plate is zero. The dimensionless displacements increase sharply with the gradient distribution index. The dimensionless radial stress changes nonlinearly along the thickness direction of the plate and presents compressive stresses in the thickness direction of the plate and changes sharply with the gradient distribution index. Compare with the simply supported condition, the clamped condition can provide greater constraint effects. As can be found, the dimensionless deflection is smaller than that of the simply supported plate and the dimensionless radial stress is bigger than that of the simply supported plate.
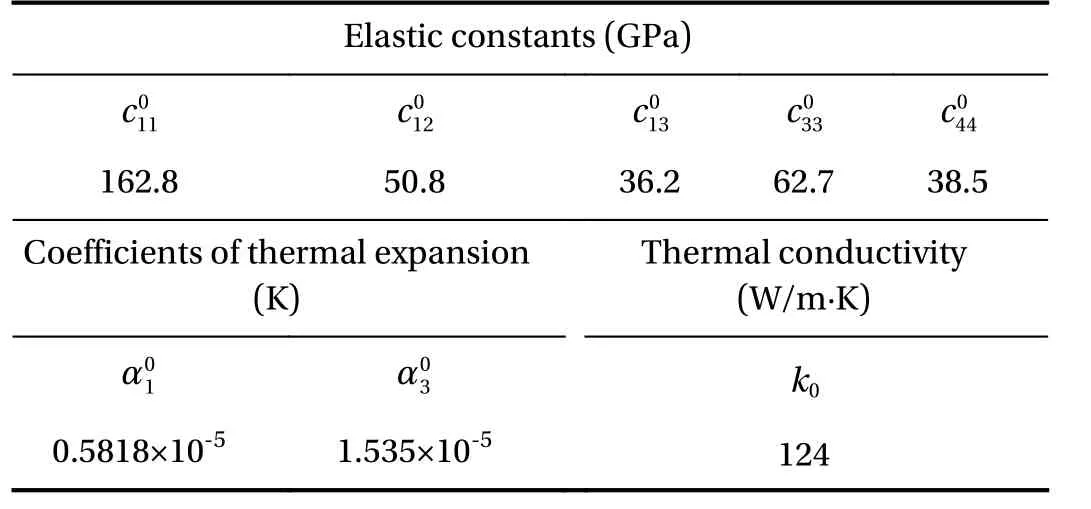
Table 1 Material properties of hexagonal zinc
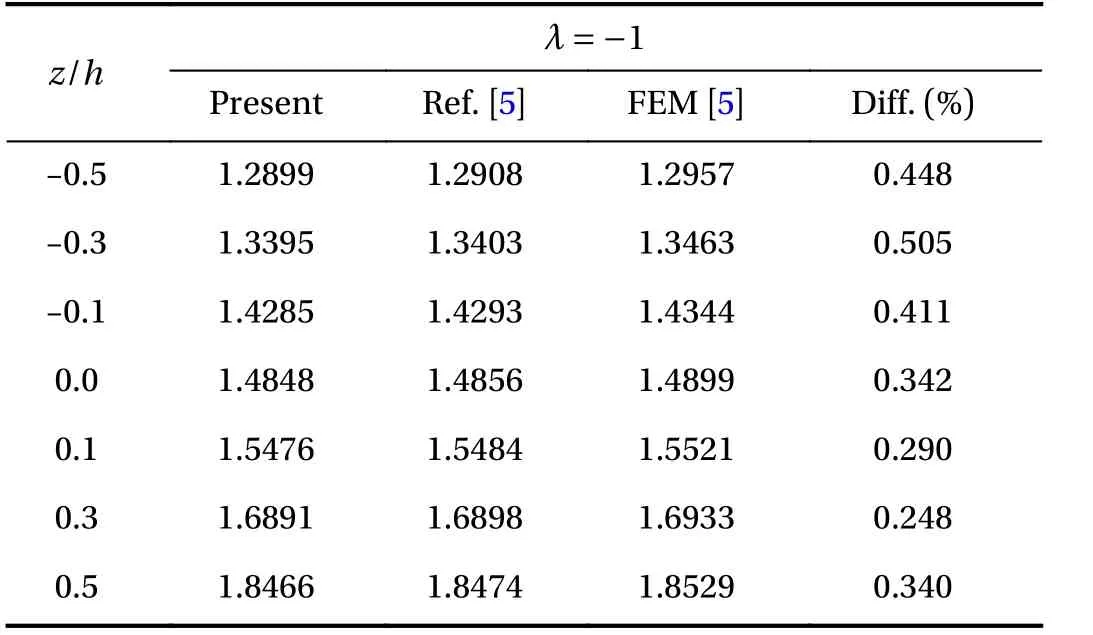
Table 2 Dimensionless deflection W= (w/h)×103
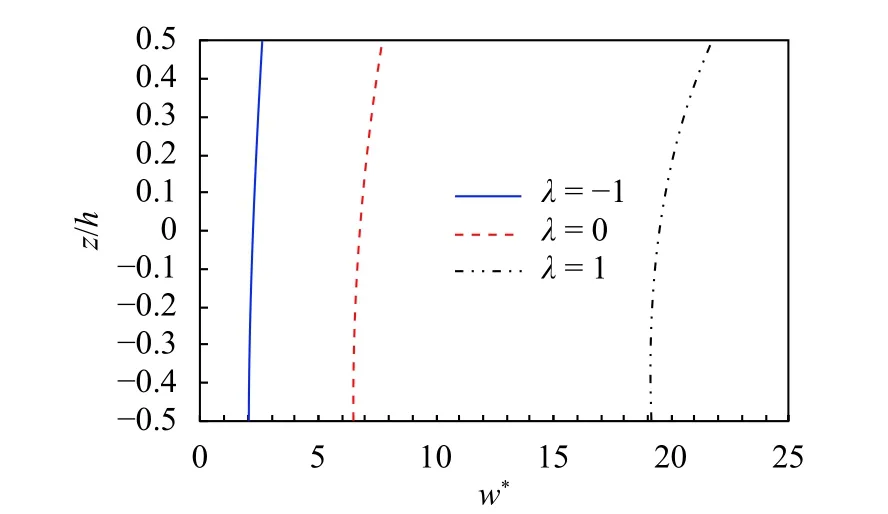
Fig. 2. Distribution of the dimensionless displacement along the thickness direction of the simply supported annular plates

Fig. 3. Distribution of the dimensionless radial stress along the thickness of the simply supported annular plates
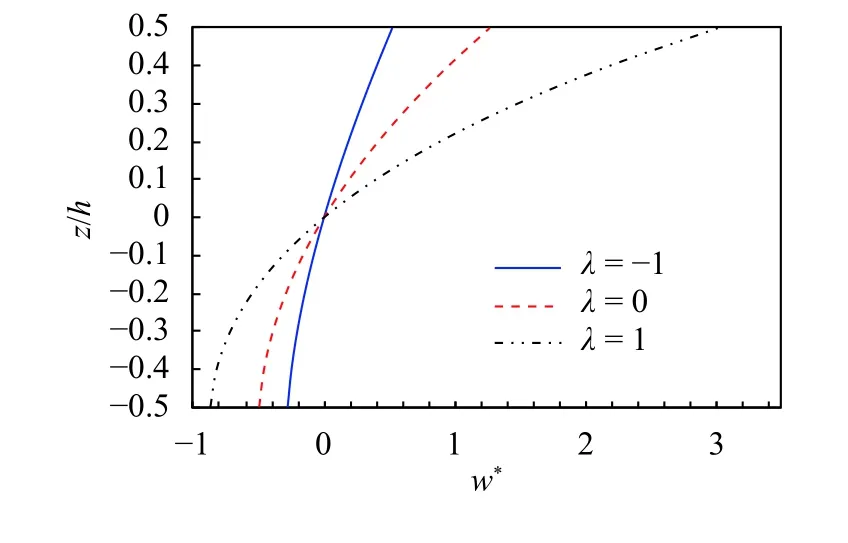
Fig. 4. Distribution of the dimensionless displacement along the thickness direction of the clamped annular plates
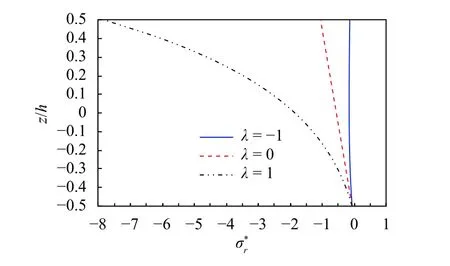
Fig. 5. Distribution of the dimensionless radial stress along the thickness of the clamped annular plates
Figures 6 and 7 show the dimensionless radial stressof the simply and clamped supported annular plates under different temperature fields. By comparing the two results, it is shown that the dimensionless radial stresses are affected by different temperature fields where the bottom surface temperature with a lower value has a greater influence than the temperature difference between top and bottom surfaces of the plates.
Figures 8 and 9 present the dimensionless radial stressof the simply and clamped supported annular plates with different a/b values. By comparing the two results, it is shown that the different a/b ratio only affects the dimensionless radial stress of the simple supported plates due to its strong constraint of the clamped condition.

Fig. 6. Distribution of the dimensionless radial stress along the thickness of the simply supported annular plate under a temperature change

Fig. 7. Distribution of the dimensionless radial stress along the thickness of the clamped the clamped annular plates annular plate under a temperature change
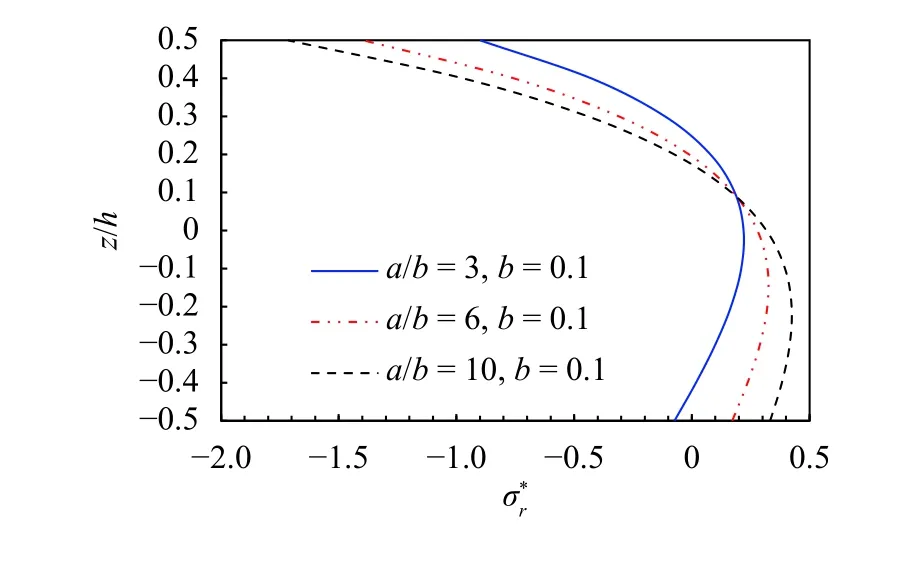
Fig. 8. Distribution of the dimensionless radial stress along the thickness of the simply supported annular plate with different a/b
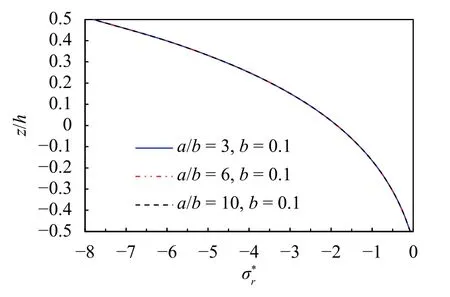
Fig. 9. Distribution of the dimensionless radial stress along the thickness of the clamped the clamped annular plates annular plate with different a/b
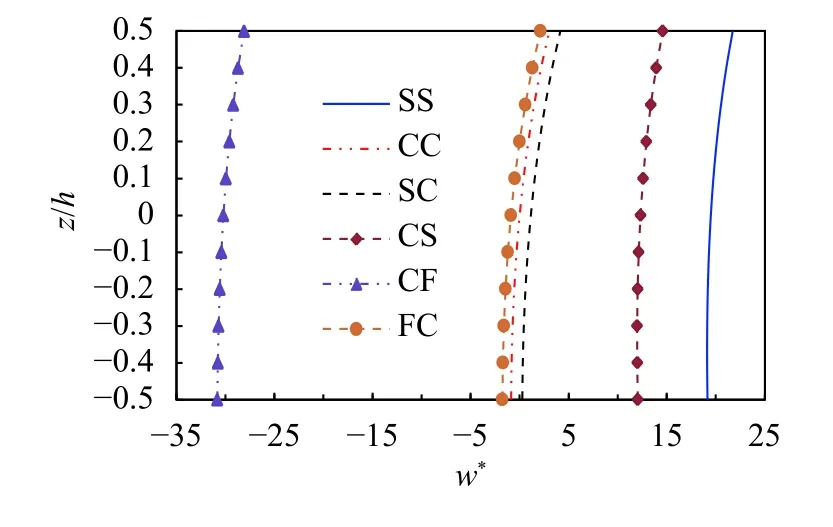
Fig. 10. Distribution of the dimensionless displacement along the thickness of the annular plate with different boundary conditions
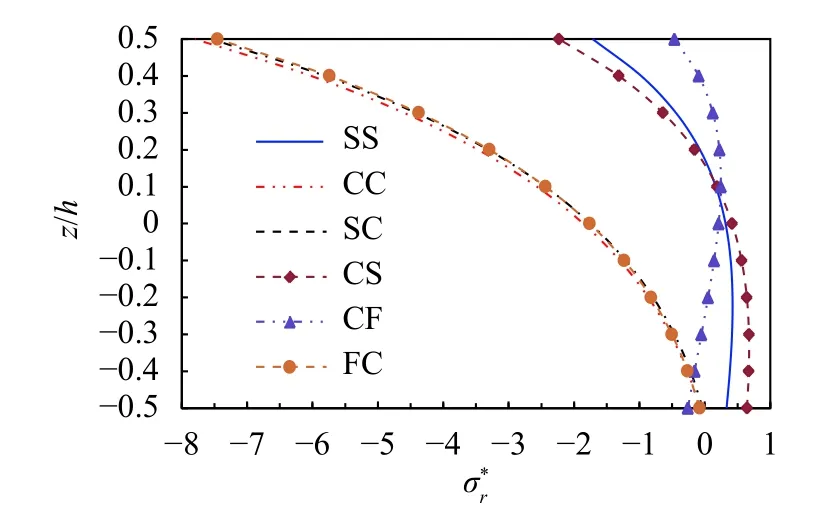
Fig. 11. Distribution of the dimensionless radial stress along the thickness of the annular plate with different boundary conditions
In order to study the influences of different combinations of boundary conditions on deflection and stress of the annular plates, Figs. 10 and 11 draw the dimensionless deflection w*and radial stressof the annular plates with different boundary conditions. When the internal and external boundaries are simply supported, the positive dimensionless displacement is the largest, and when the internal boundary is clamped and the external boundary is free, the negative dimensionless displacement is the minimum. The dimensionless radial stress along the thickness direction is nonlinearly distributed, and those of CC(annular plates clamped on outside and inside) plate and FC(free on inside and clamped on outside) plate are relatively close and vary greatly.
In this paper, the thermoelastic response of functionally graded annular plates is studied based on the Main and Spencer plate theory. The temperature field is caused by the thermal conduction in the thickness direction of the plate. It is found from the parametric study that the distribution pattern of material,the gradient index, boundary conditions, temperatures on the top and bottom surfaces and inner and outer radius ratio have different effects on the FGM annular plates. The thermally induced behavior of functionally graded annular plates can be optimized through the reasonable design of the above factors based on our research. The present elasticity solutions can also be used a benchmark to access the validity and accuracy of various simplified plate theories or numerical methods which are used in the study of such plates.
Acknowledgements
The work was supported by the National Natural Science Foundation of China (Grant 11872336) and the Natural Science Foundation of Zhejiang Province, China (Grant LY18A020009).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Thermal Stresses
- Stresses of orthotropic laminated beams subjected to high temperature and mechanical load
- Thermoelastic stability of closed cylindrical shell in supersonic gas flow
- Transient thermal response of functionally graded piezoelectric laminates with an infinite row of parallel cracks normal to the bimaterial interface
- Stochastic transient analysis of thermal stresses in solids by explicit timedomain method
- Thermoelastic waves in helical strands with Maxwell-Cattaneo heat conduction
