Stochastic transient analysis of thermal stresses in solids by explicit timedomain method

Houzuo Guo, Cheng Su,b,*, Jinhu Xin

a School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China

b State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510640, China

Keywords:Stochastic Non-stationary Heat conduction Thermal stress Explicit time-domain method

A B S T R A C T Stochastic heat conduction and thermal stress analysis of structures has received considerable attention in recent years. The propagation of uncertain thermal environments will lead to stochastic variations in temperature fields and thermal stresses. Therefore, it is reasonable to consider the variability of thermal environments while conducting thermal analysis. However, for ambient thermal excitations, only stationary random processes have been investigated thus far. In this study, the highly efficient explicit time-domain method (ETDM) is proposed for the analysis of non-stationary stochastic transient heat conduction and thermal stress problems. The explicit time-domain expressions of thermal responses are first constructed for a thermoelastic body. Then the statistical moments of thermal displacements and stresses can be directly obtained based on the explicit expressions of thermal responses. A numerical example involving non-stationary stochastic internal heat generation rate is investigated. The accuracy and efficiency of the proposed method are validated by comparison with the Monte-Carlo simulation.

Traditional thermal analysis generally assumes deterministic thermal environments. In fact, the environmental parameters,e.g., internal heat generation rate, heat flux, boundary temperature and ambient temperature, etc., are difficult to measure and predict accurately. Therefore, the variability of the thermal environments should be considered to reflect the uncertainty propagation involved in the thermal stress problems.

Over the past few decades, researchers have solved the problems of statistical moments of temperatures and thermal stresses of several simple structures under random internal heat generation rate, heat flux, boundary temperature or ambient temperature with analytical methods, in which the thermal environments are modeled in the form of random variables or stationary random processes [1-3]. However, for practical problems, the thermal excitations involved often exhibit non-stationary characteristics due to the time-varying statistical properties of thermal environments, and therefore should be modelled as non-stationary random processes.

In this study, the explicit time-domain method (ETDM) [4, 5],originally proposed for non-stationary random vibration analysis of structures, is applied to the analysis of non-stationary stochastic heat conduction and thermal stress problems. The explicit time-domain expressions of temperatures, thermal displacements and thermal stresses are first established. Then, the statistical moments of temperatures and thermal responses can be directly obtained from the statistical properties of non-stationary thermal excitations.

The governing equation of a two-dimensional transient heat conduction problem can be expressed as

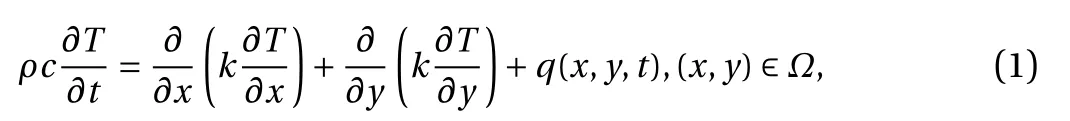
where Ω denotes the domain under consideration;T=T(x,y,t)is the temperature field at time t ; ρ , c , and k are the mass density, the specific heat and the thermal conductivity,respectively; and q (x,y,t) is the internal heat generation rate.

The boundary conditions are given as follows:

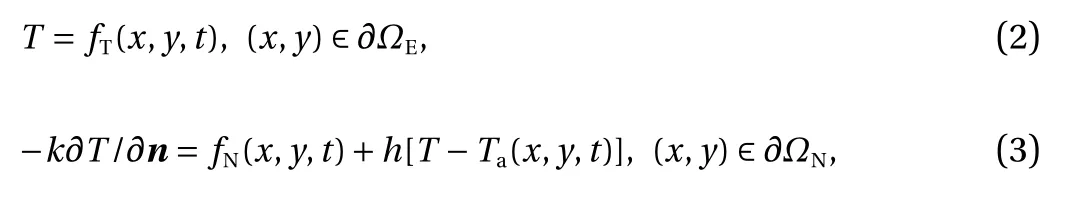
where ∂ ΩEand ∂ ΩNare the essential boundary and the natural boundary, respectively; n is the outward normal vector of the boundary; fT(x,y,t) and fN(x,y,t) are the temperature function and the heat flux function along ∂ ΩEand ∂ ΩN, respectively; h is the convective heat transfer coefficient; Ta(x,y,t) is the ambient temperature.

The finite element form of Eqs. (1)-(3) can be derived as [6]

The transient temperature vector T (t) of a plate will cause transient thermal displacements and stresses, and the equation of motion of the plate can now be expressed as

where B, D and N are the displacement-strain matrix, the stressstrain matrix and the temperature shape function matrix of the element, respectively; α is the linear thermal expansion coefficient; t¯ is the thickness of the plate.

Introduce a state vector defined as

Then, Eqs. (4) and (5) can be combined into the following state equation:

where

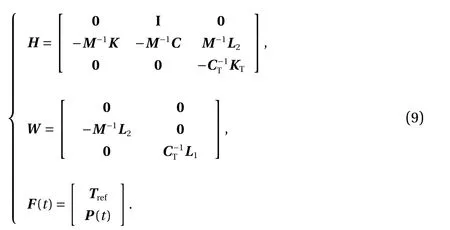
For Eq. (8), the initial condition can be assumed asin which T0is the initial temperature vector.

Solving Eq. (8) for the state vector V , one can get the temperatures and thermal displacements of the plate. Using the constitutive relationship, one can further obtain the thermal stresses of the plate.

To reflect the physical evolution process of the thermoelastic problem governed by Eq. (8), the explicit time-domain expression of the state vector V (t) is first derived. For linear problems,V(t) can be expressed as a linear combination of F (t) at different time instants as follows:

where Vi=V(ti) and ti=iΔt(i=1,2,···,n), in which Δ t and n are the time step and the number of time steps, respectively;Vi,0represents the contribution to Vicaused by the initial vector V0;Fj=F(tj)(j=0,1,···,i); and Ai,j(j=0,1,···,i) are the coefficient matrices associated with the thermal and structural parameters,representing the influence of Fj( j=0,1,···,i) on Vi.

The coefficient matrices Ai,jcan be derived in closed forms from Eq. (8) as [4, 5]

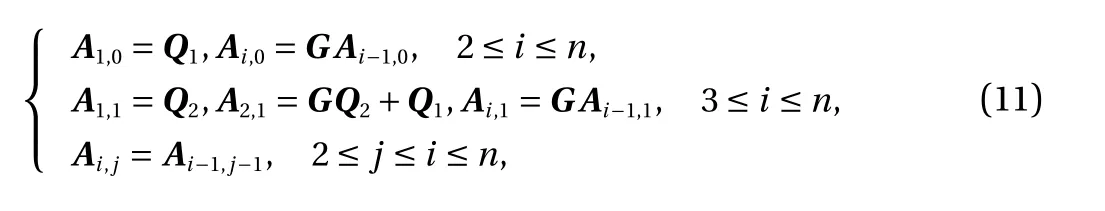
where G, Q1and Q2can be obtained depending on different integration schemes.

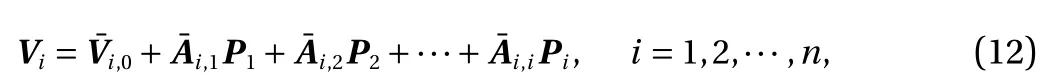
where the coefficient matricescan be extracted from the coefficient matrices Ai,j(j=1,2,···,i); the influence of Trefat different time instants is included in

For better understanding, the coefficient matrices shown in Eq. (12) are also presented in Table 1. It can be seen from Table 1 that only the coefficient matricesneed to be calculated and stored. Furthermore, the k-th columns in the coefficient matricesrepresent the state vector of the plate at time ticaused by the unit impulse excitation pk(t) corresponding to the k-th thermal excitation Pk(t) ( k=1,2,···,m), as shown in Fig. 1. Therefore, the coefficient matricescan also be obtained by m transient analyses directly using commercial finite element software.

Thus far, the physical evolution mechanism of the thermoelastic problem has been completely reflected by Eq. (12). On this basis, the statistical evolution mechanism can be further considered by moment operation rule.

Note that, for structural design, not all the responses are required, and only a certain number of critical responses need to be focused on. Assume riis one of the temperatures or thermal displacements in Vi. Then, the explicit expression for rican be directly obtained from Eq. (12) as follows:

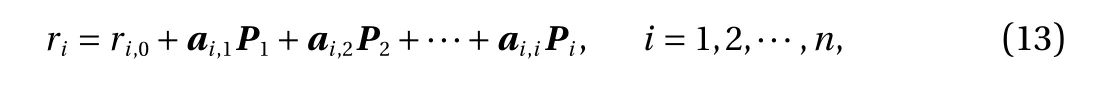
where ri,0and ai,j(j=1,2,···,i) are the corresponding rows extracted fromandrespectively. When ridenotes a thermal stress, the constitutive law needs to be considered for obtaining ri,0and ai,j(j=1,2,···,i) from the explicit expressions of the associated displacements.

From Eq. (13), the mean and the variance of the response rican be obtained as

andrespectively, in which μP(t) and RPP(t,τ) are the mean function vector and the cross-correlation function matrix of P(t),respectively.

Table 1 Coefficient matrices for state vector

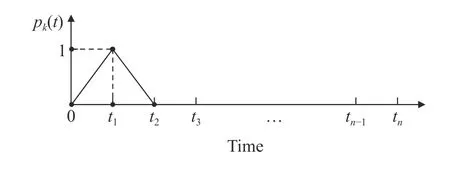
Fig. 1. Unit impulse excitation applied at

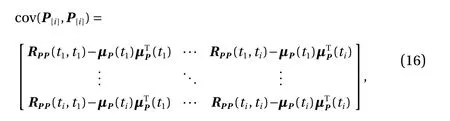
It can be seen from Eq. (14) that dimension-reduced statistical moment analysis can be easily conducted owing to the explicit formulation shown in Eq. (12), which will lead to significant reduction in computational cost for stochastic thermal analysis.Further, in the above formulation, the correlation functions rather than the power spectral density functions of the thermal excitations are required. Therefore, Eq. (14) can be applied to non-stationary stochastic analysis without any difficulties.

Consider a square plate with thickness=0.01 m, as shown in Fig. 2. The material parameters of the plate are listed in Table 2.

The bottom edge of the plate is fixed, and all the plate edges are adiabatic. The plate is divided into 1 0×10 plate elements, as shown in Fig. 2.take nas 10°C for the whole domain. The plate is subjected to a

The initial temperature and the reference temperature are uniform distributed internal heat generation rate modeled as a zero-mean non-stationary Gaussian process:

where g (t)=4(e-0.1t-e-0.2t) is a modulation function; q (t) is a S0=1.0×108J2/(m6·s).stationary white noise process with spectral density being

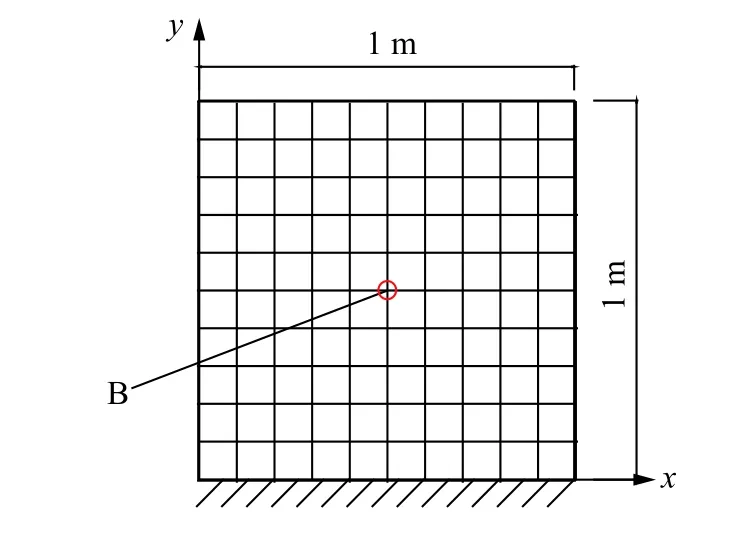
Fig. 2. A square plate

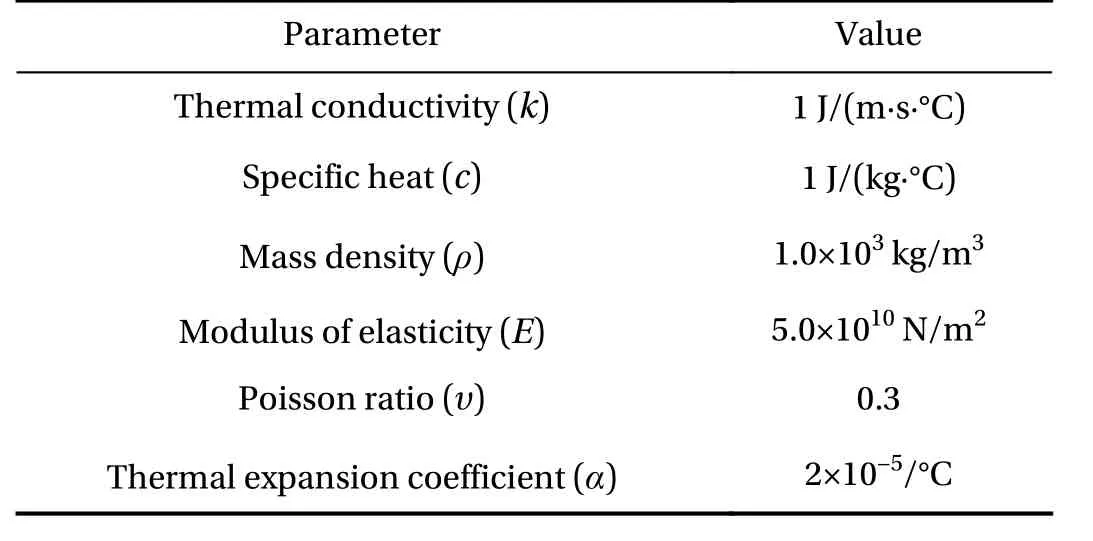
Table 2 Material parameters

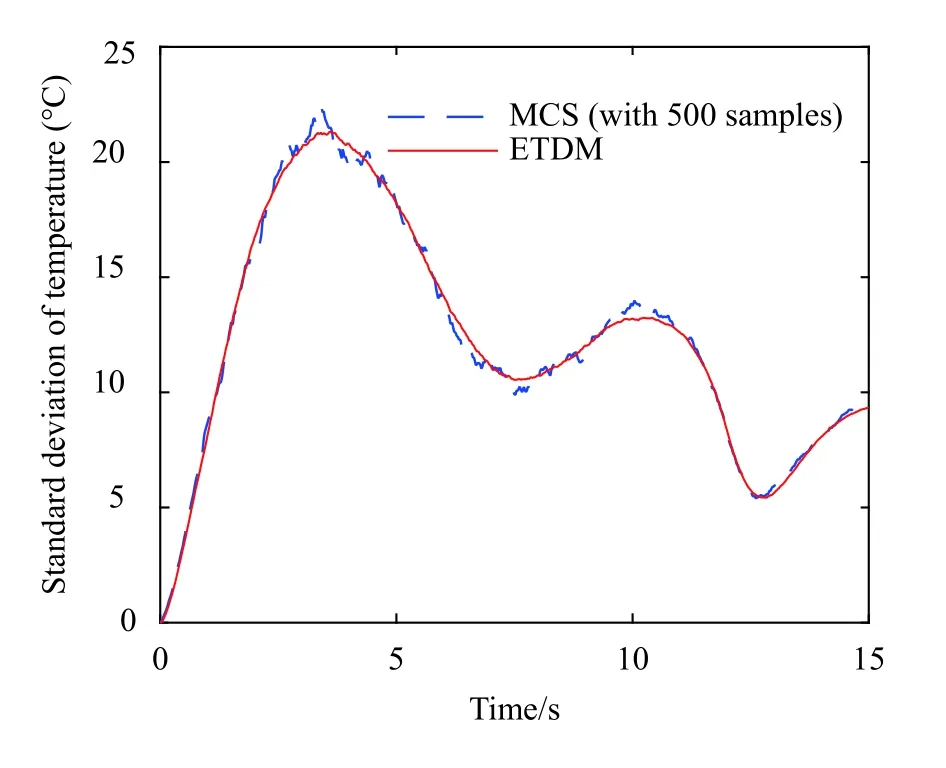
Fig. 3. Standard deviation of temperature at node B

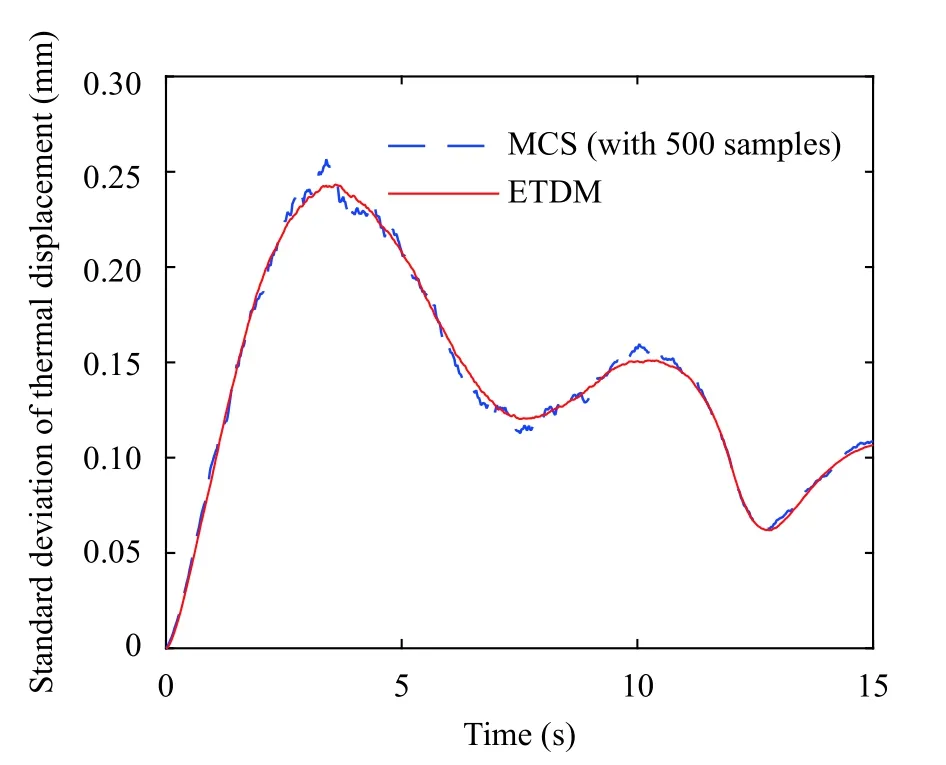
Fig. 4. Standard deviation of thermal displacement in Y direction at node B

The statistical moments of temperatures and thermal stresses of the plate are calculated by the proposed ETDM. For the purpose of comparison, the Monte-Carlo simulation (MCS)with 500 samples is conducted on ANSYS software platform. The duration of the time-history analysis is set to be 15 s with the time step being Δ t=0.02 s.

The standard deviations of the temperature and the thermal displacement and stress at node B are presented in Figs. 3-5, respectively. It can be observed from the figures that the results obtained with ETDM and MCS are in good agreement, indicating the high accuracy of the proposed method. For comparison of the calculation efficiency, the time elapsed by the two methods is presented in Table 3, from which it can be seen that the computational time of ETDM is 398 s, showing the high efficiency of the present approach.

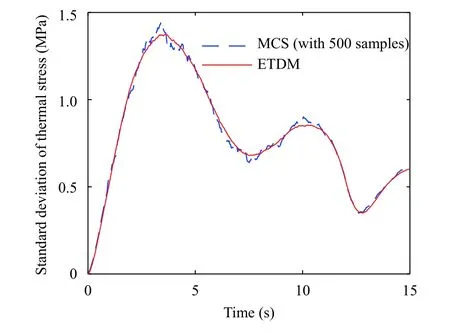
Fig. 5. Standard deviation of thermal normal stress in Y direction at node B

Table 3 Comparison of the time elapsed by different methods

A highly efficient ETDM has been proposed for non-stationary stochastic transient heat conduction and thermal response analysis. The explicit expressions of temperatures and thermal displacements and stresses are first established in terms of stochastic thermal excitations, and the dimension-reduced statistical moment analysis is then conducted based on the explicit formulations. A numerical example has been investigated to show the high accuracy and efficiency of the proposed method.

ACKNOWLEDGEMENTS

The research is funded by the National Natural Science Foundation of China (51678252) and the Guangzhou Science and Technology Project (201804020069)