Stresses of orthotropic laminated beams subjected to high temperature and mechanical load
2019-11-04ZhongZhangDingZhouXiuliXuXuehongLi
Zhong Zhang, Ding Zhou, Xiuli Xu, Xuehong Li
College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China
Keywords:Orthotropic laminated beams Temperature-dependent material properties Thermo-elasticity theory State space method Transfer-matrix method
A B S T R A C T Thermo-elastic analysis of simply-supported orthotropic laminated beams subjected to high temperature and mechanical load is presented on the basis of the exact two-dimensional thermoelasticity theory. The beam is composed of several orthotropic layers, each with temperaturedependent material properties. The governing equation for each layer is analytically solved using the state space method. The displacement and stress solutions of the beam are obtained using the transfer-matrix method. A numerical example is included to study the effects of temperature on the mechanical responses of a sandwich beam. The results reveal two main effects of temperature:(i) inducing deformations and stresses by itself; (ii) affecting the deformations and stresses induced by the mechanical load.
The excellent mechanical property and environmental sustainability of composite structures have led to their use in modern engineering [1]. The mechanical performance of these structures under high temperature environment has attracted considerable attention, since the temperature could reduce the loadcarrying capacity of the structures, and even cause structural failure.
Several theories are available in literature for beam problems [2]. Timoshenko [3] studied the thermo-elastic behavior of two-layer beams under uniform heating based on the Euler-Bernoulli theory. This work had been developed by Suhir [4] for evaluating the distribution of the shear and normal stresses along the interface. The thermal deformations in cross-ply composite beams were studied by Khdeir and Reddy [5], based on the Euler-Bernoulli theory, first-order theory, second-order theory, and third-order theory. Zhang et al. [6, 7] carried out the elasticity solution of displacements and stresses for isotropic laminated beams under thermo-mechanical loads.
In this work, simply-supported orthotropic laminated beams under high temperature and mechanical load are investigated based on the thermo-elasticity theory, in which no transverse shear deformation hypothesis is used compared with the classical theory and various shear deformation theories. The effects of temperature on the thermo-elastic behavior of the beams are discussed.
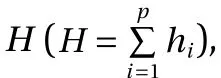
We consider an arbitrary layer i (i=1, 2, …, p) with a local coordinate system (x, yi), as shown in Fig. 1(b). Assuming that the principal material axes coincide with the coordinate axes and that the layer is in the plane stress state. In this case, the thermoelastic constitutive relations are [8]
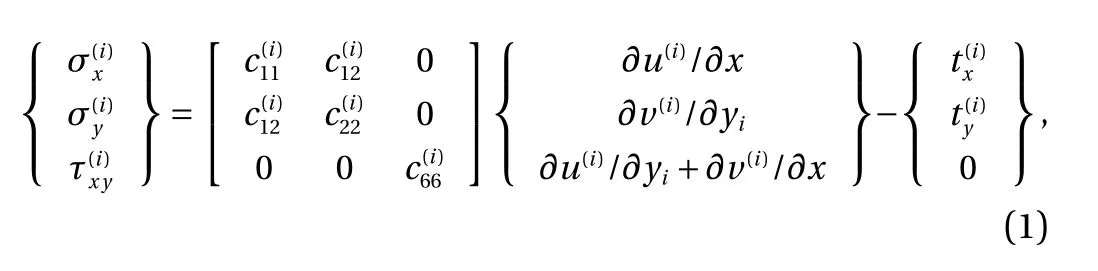
where
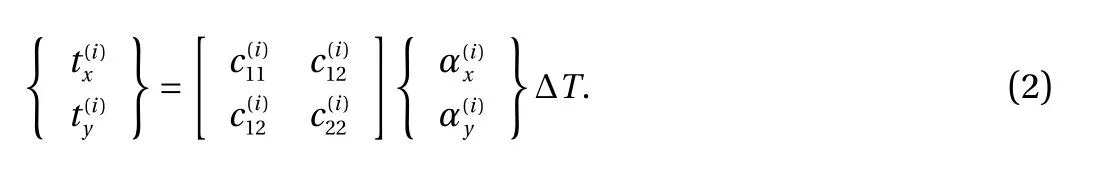
In Eqs. (1) and (2), u(i)and v(i)are the displacement components;andare the stress components;andare the thermal expansion coefficients;are the orthotropic stiffnesses, which are expressed in terms of the engineering constants by

The equilibrium equations are
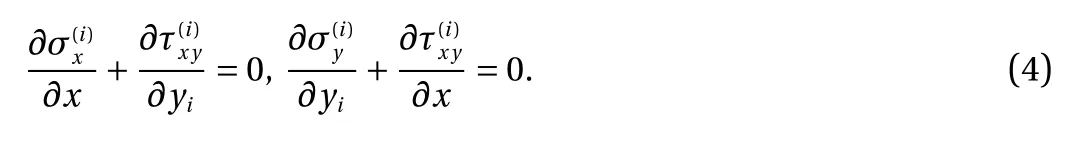
The simply-supported conditions are

where the stress boundary conditions can be rewritten by substituting Eq. (1) into the second of Eq. (5) as

Fig. 1. Geometric size and coordinate system of an orthotropic laminated beam. a Orthotropic laminated beam. b Layer i.
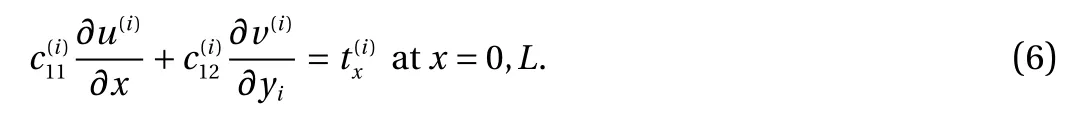
The right side of Eq. (6) can be assumed as the surface forces in the x direction. Therefore, the displacements of layer i induced by the uniform thermal load in the x direction are equivalent to those induced by the normal surface forces acted at the two lateral ends. In this case, the stresscan be expressed by
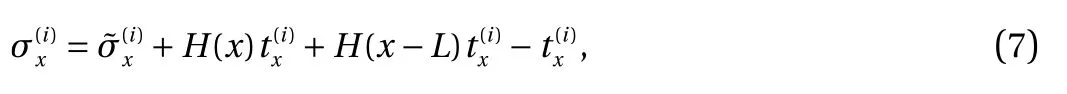
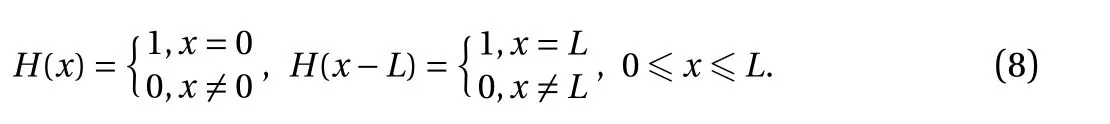
Applying Eq. (7) into Eq. (4) yields
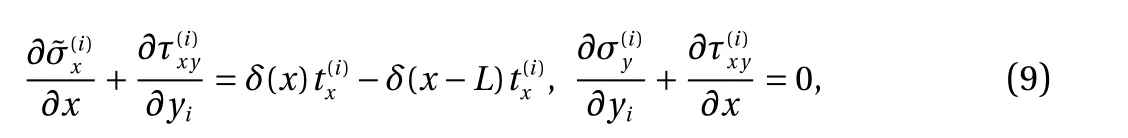
where δ(x) and δ(x-L) are the Dirac delta functions defined as
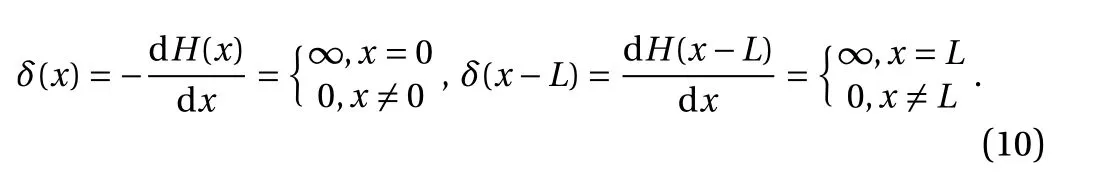
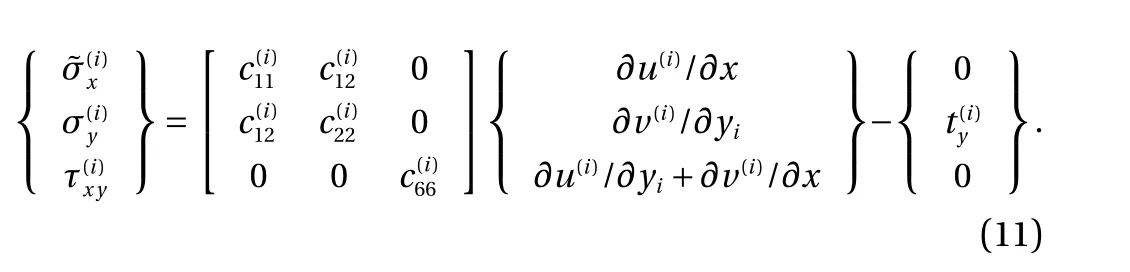
Combining Eqs. (9) and (11) gives

where
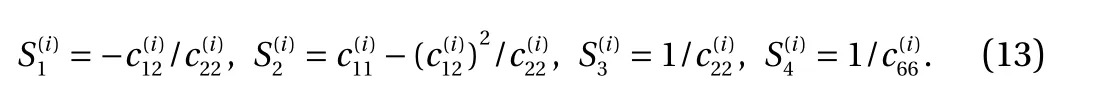
Expanding the Dirac delta functions in Eq. (12) gives:

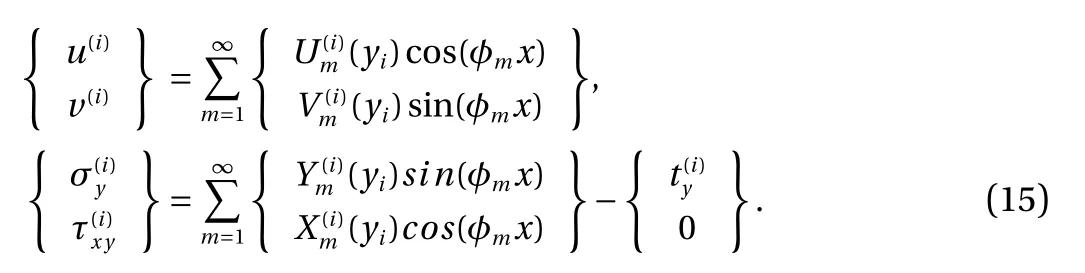
Substituting the solutions of u(i)andinto Eq. (11) gives
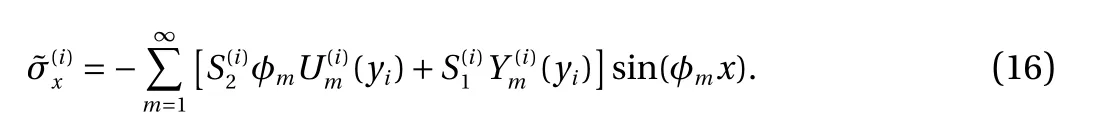
Accordingly, applying the solution ofto Eq. (7) obtains the stress
Applying Eqs. (14) and (15) to Eq. (12) yields

where
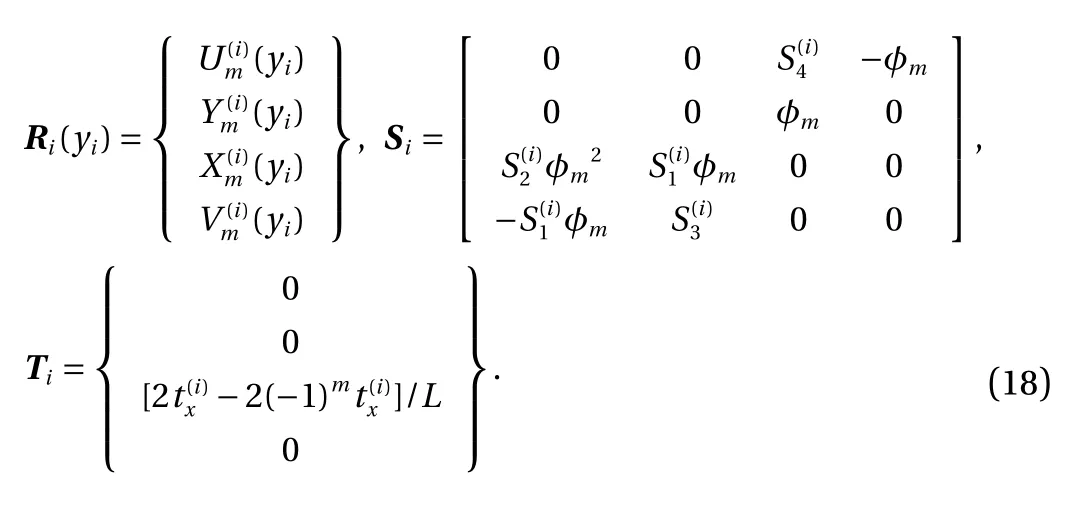
The solution of Eq. (17) is

where

where I is a 4×4 unit matrix.
Taking yi=hiand yi+1=hi+1into Eq. (19) gives

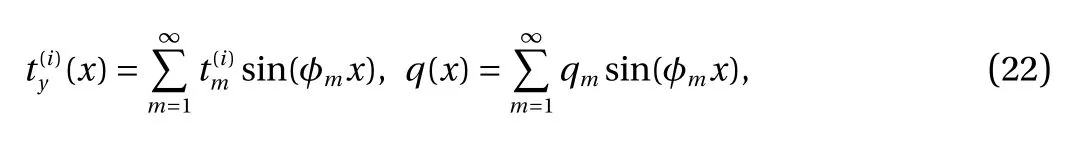
where

The interfacial continuity conditions between adjacent layers are
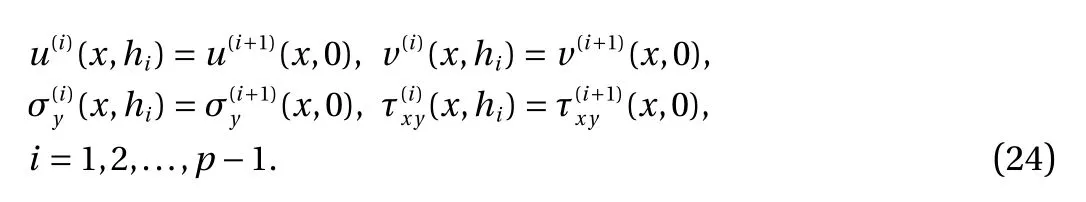
Applying Eqs. (15) and (22) to Eq. (24) gives

where
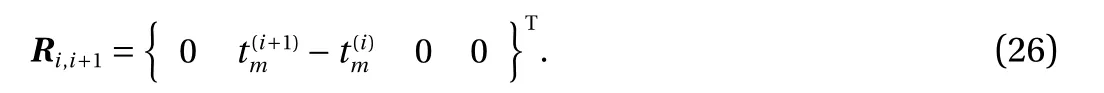
Combining Eqs. (21) and (25) gives
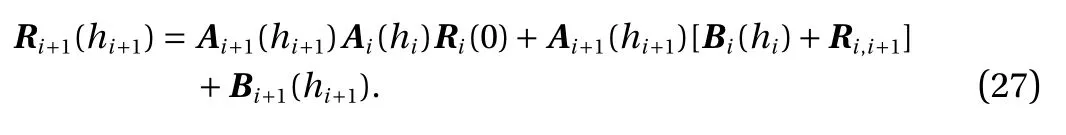
By analogy, the relation between layer k and the bottom layer is
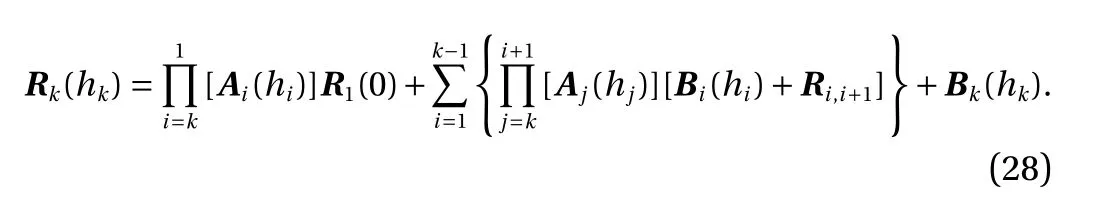
The top and bottom surface conditions are
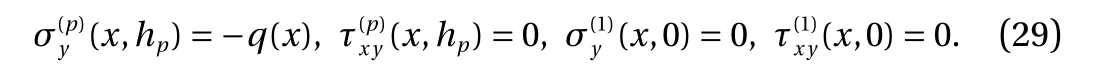
Applying Eqs. (15) and (22) to Eq. (29) gives

Substituting Eq. (30) into Eq. (28) gives
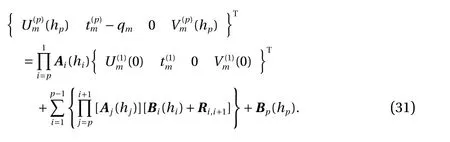
The convergence of present solution should be checked since it is expressed in the form of Fourier series. The displacements and stresses can be numerically solved by truncating the series terms m up to M, i.e. m=1, 2, …, M. Consider a sandwich beam, as shown in Fig. 2. The top and bottom layers are identical with the temperature-dependent material properties shown in Table 1. The temperature-independent material properties of the soft core are [9]: Ex=1 GPa, Ey=2 GPa, Gxy=0.8 GPa, μxy=0.25,αx=αy=30×10-6°C-1. Some parameters are: L=4 m,h1=h3=0.1 m, h2=0.8 m, q(x)=10 kN/m, T0=20 °C, T=100 °C. Table 2 shows the convergence study of the displacement and stress components at x=0.25L for the sandwich beam. The data show a good convergence of the present solution. The displacement and stress obtained at M=35 can guarantee satisfied accuracy, hence the truncated terms are taken as M=35 in the following analysis unless stated.
In order to show the effects of temperature on the structure responses, we divide the load conditions of the laminated beam into two parts: Part A represents that the beam is only subjected to the thermal load, i.e. the mechanical load q(x)=0; Part B represents that the beam is only subjected to the mechanical load(but the effects of temperature on the material properties are still considered), which can be achieved by setting the thermal expansion coefficient to be zero. Therefore, the displacement and stress solutions are expressed by
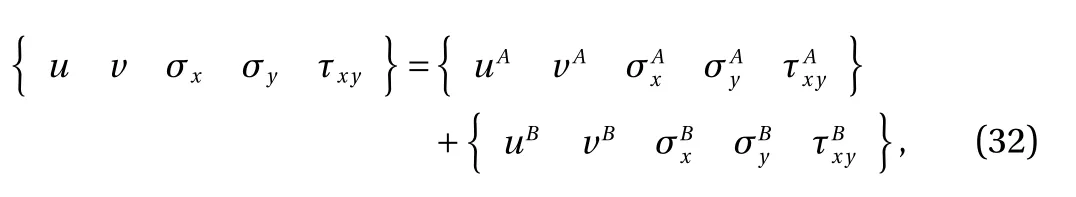
where the symbols A and B denote the displacement and stress components of Part A and Part B, respectively. In the following analysis, two states are considered: (i) the material properties are temperature-dependent (TD); (ii) the material properties are temperature-independent (TID), and they are taken as those at T0=20 °C.
Firstly, the deformations and stresses of Part A are studied.Figure 3 shows the distributions of vAandat x=0.25L for the sandwich beam under different temperatures T=70, 120, and 170°C. It is seen that vAandincrease with the increase of T. When T is fixed, the displacement of the top and bottom layers in the TD state is greater than that in the TID state (see Fig. 3(a)), due to the reduction of the stiffness when considering the temperature-dependent properties. However, the distributions of vAandin the core layer are almost invariable in the two states, since the material properties of the core layer are temperature-independent. It is found from Fig. 3(b) thathas a sudden change on the interfaces, due to the different material properties between adjacent layers. Figure 4 shows the variations of vAandandat the interface x=0.25L, y=0.1H with respect to the temperature T. In Fig. 4,andlinearly increase in the TID state as T rises, while they nonlinearly increase in the TD state. The discrepancies of vAandbetween the two states increase as T rises, while the discrepancy ofbetween the two states is small.
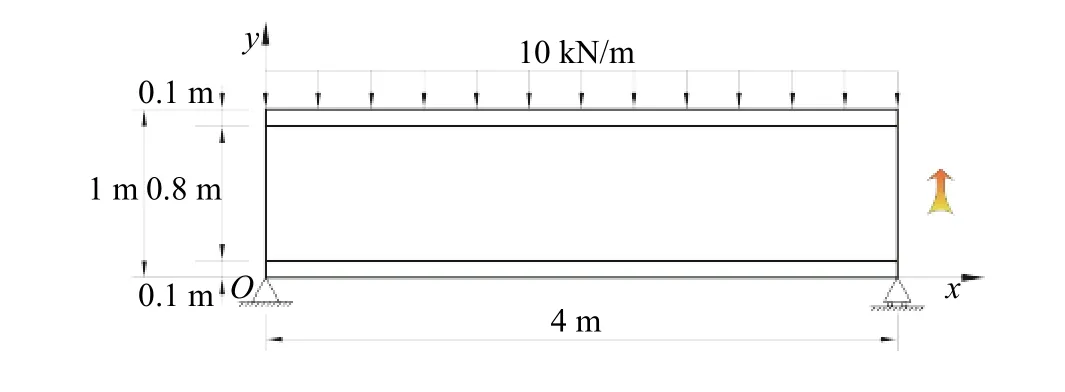
Fig. 2. Simply-supported sandwich beam under thermo-mechanical load.
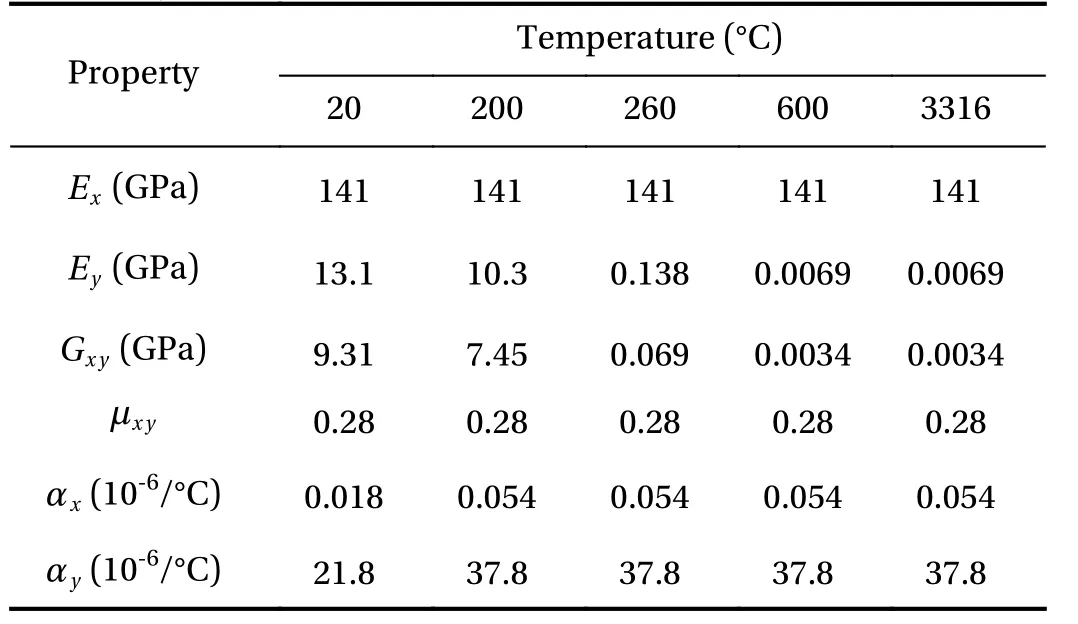
Table 1 Temperature-dependent material properties of the top and bottom layers [10].
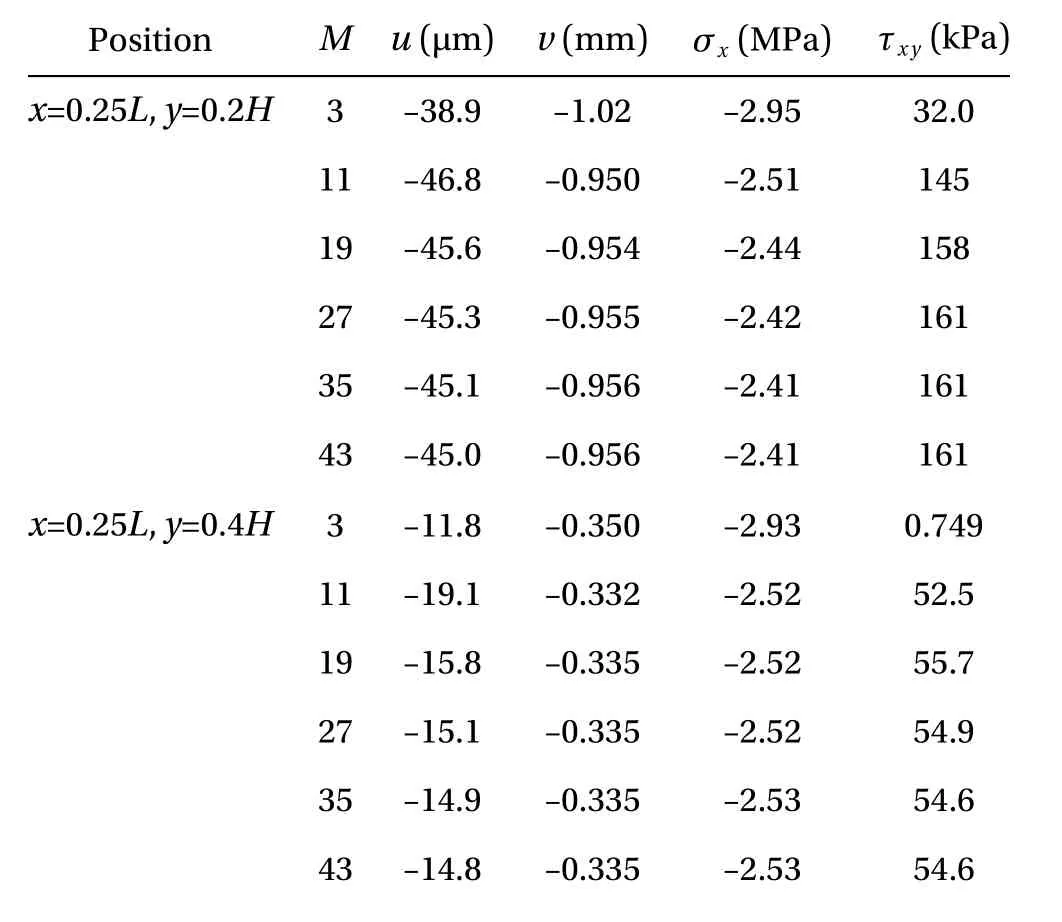
Table 2 Convergence study of the present solution.
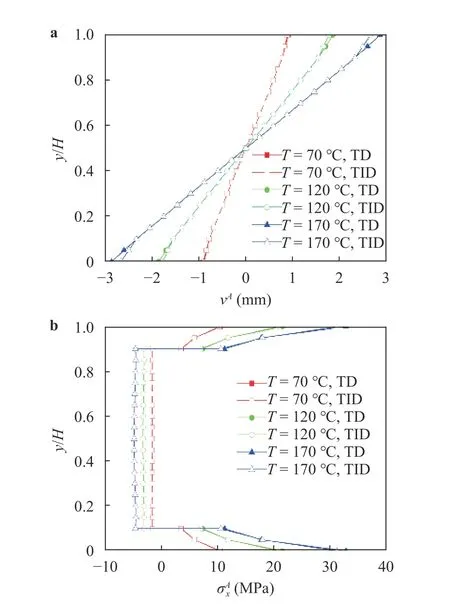
Fig. 3. Displacement and stress distributions at x=0.25L for the sandwich beam subjected to the thermal load. a Displacement.b Stress.
Then the deformations and stresses of Part B are studied. Fig-ure 5 displays the distributions of vBat x=0.5L andat x=0 for the sandwich beam. It is seen from Fig. 5(a) that vBin the TD state is increased with the increase of temperature; vBin the TID state is smaller than that in the TD state. Figure 5(b) shows thatis almost invariable in the two state.
In summary, thermo-elastic analysis of simply-supported orthotropic laminated beams with temperature-dependent material properties is carried out. In the numerical example, the responses of a sandwich beam induced by the thermal load and mechanical load are separately studied. Some important points are summarized:

Fig. 4. Displacements and stresses versus the temperature for the sandwich beam subjected to the thermal load. a Displacement at x=0.25L, y=0. b Stress at x=0.25L, y=0. c Stress at x=0.25L,y=0.1H.
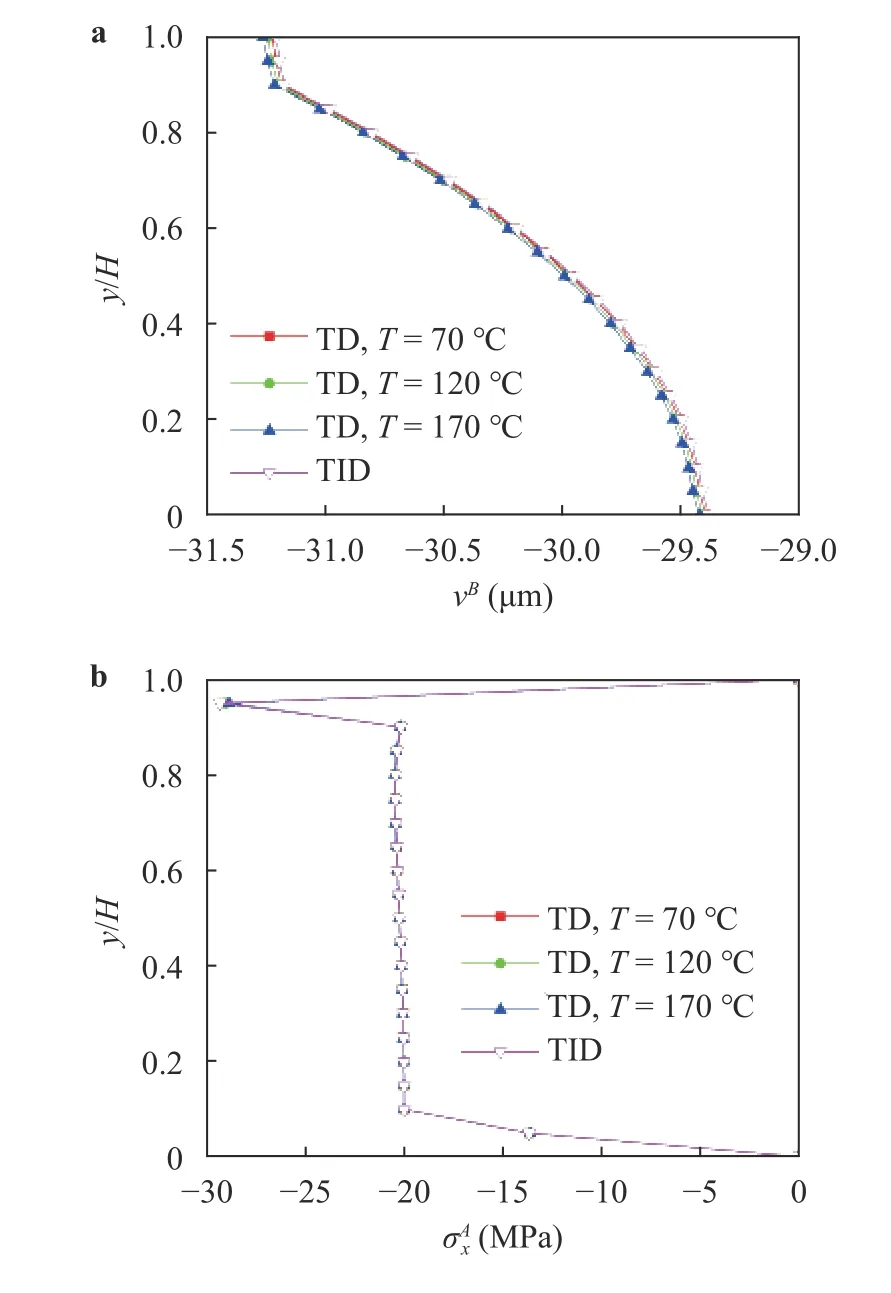
Fig. 5. Displacement and stress distributions for the sandwich beam subjected to the mechanical load, considering the effects of temperature on the material properties. a Displacement at x=0.5L. b Stress at x=0.
(1) When the beam is only subjected to the thermal load, the displacements and stresses linearly vary with the temperature in the temperature-independent state; however, nonlinearly vary in the temperature-dependent state. The discrepancy between the two states is increased as the temperature rises.
(2) When the beam is only subjected to the mechanical load,the deformations of the beam are more affected by the temperature compared with the stresses.
(3) The results reveal two main effects of temperature on the mechanical responses of the beam: (i) inducing deformations and stresses by itself; (ii) affecting the deformations and stresses induced by the mechanical load.
Acknowledgement
This work is financially supported by the National Natural Science Foundation of China (51778289), the Transportation Science and Technology Project of Jiangsu Province (2014Y01),and the Science and Technology Plan Project of Jiangsu Province(BY2016005-12).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Thermal Stresses
- Thermoelastic stability of closed cylindrical shell in supersonic gas flow
- Transient thermal response of functionally graded piezoelectric laminates with an infinite row of parallel cracks normal to the bimaterial interface
- Stochastic transient analysis of thermal stresses in solids by explicit timedomain method
- 3D thermally induced analysis of annular plates of functionally graded materials
- Thermoelastic waves in helical strands with Maxwell-Cattaneo heat conduction
