Thermoelastic stability of closed cylindrical shell in supersonic gas flow
2019-11-04BghdsrynMikilynVrdnynMrzo
G.Y. Bghdsryn, M.A. Mikilyn, I.A. Vrdnyn, P. Mrzo
a Institute of Mechanics, National Academy of Sciences, Yerevan 0019, Armenia
b Russian-Armenian University, Institute of Mechanics, National Academy of Sciences, Yerevan 0019, Armenia
c Engineering, Aerospace Engineering and Aviation, Sir Lawrence Wackett Centre: Air, Space, Land, Sea School of Engineering, RMIT University, PO Box 71 Bundoora VIC 3083, Australia
Keywords:Cylindrical shell Supersonic gas flow Thermal field
A B S T R A C T In this paper the problem of linear stability of a closed cylindrical shell under the action of both non-uniform temperature field and supersonic gas flow is considered. The stability conditions for the unperturbed state of the aerothermoelastic system are obtained. It is shown that, by the combined action of the temperature field and the ambient supersonic flow, the process of linear stability can be controlled and the temperature field affects significantly the critical flutter speed.
A thin isotropic closed circular cylindrical shell of constant thickness h and radius R, located in a variable temperature field T is considered. The cylindrical coordinate system x,φ,r is chosen, the coordinate lines φ and x coincide with the curvature lines of the middle surface of the shell ( x along the generatrix and φ along the arc of the cross-section). A supersonic gas flow is considered on the outer side of the shell with an unperturbed velocity U, directed along the axis x. The stability of the aerothermoelastic system are investigated. The statement of the problem in the case of elongated plates is investigated in Ref. [1].The study is based on the following well-known assumptions:
(a) Kirchhoff hypothesis on non-deformable normals [2];
(b) Piston theory aerodynamics is used to compute the aerodynamic pressure [3]
(c) Linear law of temperature variation over the shell thickness [4]: T =T0(x,φ)+(R-r)Θ(x,φ);
(d) Neumann's hypothesis on the absence of shifts from temperature changes [5].
For simplicity and clarity, it is assumed that there is a heat exchange from the front surfaces ( r=R±h/2) of the shell with the surroundings according to Newton-Richman law (the surfaces retain a constant temperature T+and T-), and the side surfaces ( x= 0 and x =a) are thermally insulated. Then the problem of thermal conductivity has the following solution:
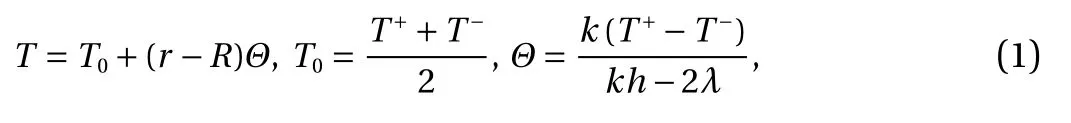
where λ is coefficient of thermal conductivity and k is coefficient of heat transfer with the temperature T measured in degree Celsius (°C).
Under the action of a stationary temperature field which is non-uniform over the thickness ( Θ0), shell buckling occurs with deflection wT(x) and longitudinal displacement uT(x) which results in aerodynamic loading. The indicated buckling state is accepted as unperturbed [6] and its stability is investigated under the action of the temperature field and the pressure of the flowing gas flow.
Based on the accepted assumptions, from the basic equations, relations and boundary conditions of the theory of thermoelasticity of thin shells, the governing aerothermoelastic equations are obtained. These are characterized by the axisymmetric state of examined system relations:
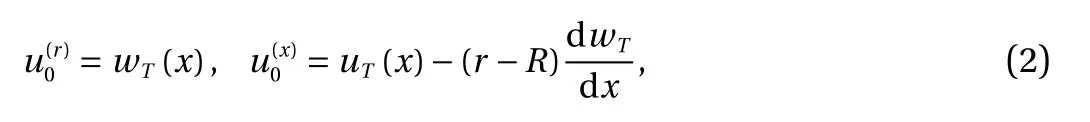
according to the Kirchhoff-Love hypothesis. These equations with respect to uTand wTare cast as follows
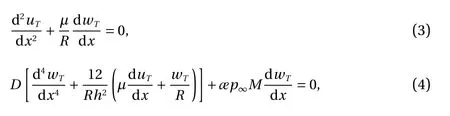
according to the theory of thin shells.
The internal forces of the unperturbed state are described as:
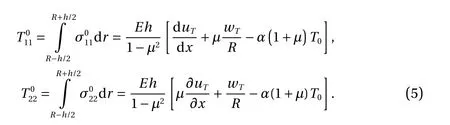
according to the generalized Hooke's law.
The solutions of Eqs. (4) and (5) must satisfy the boundary condition at the shell fixed edges x =0 and x =a. The following boundary conditions are considered:
● the edges are hinge supported and can freely move along the axis x

● the edges are hinged and immobile
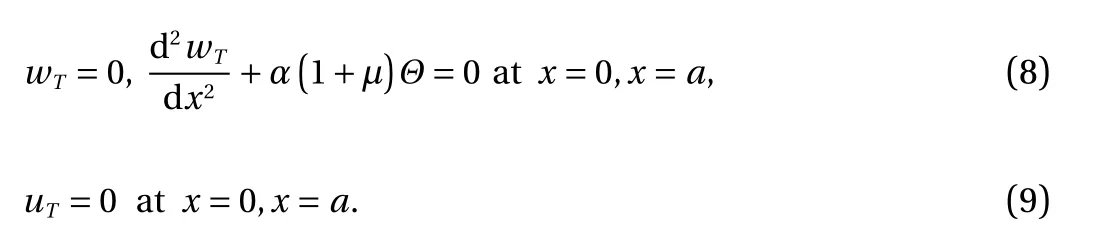
The solution uTof Eq. (4), satisfying condition Eq. (8), has the following form with the condition wT=0 on the ends of the shell is also used:
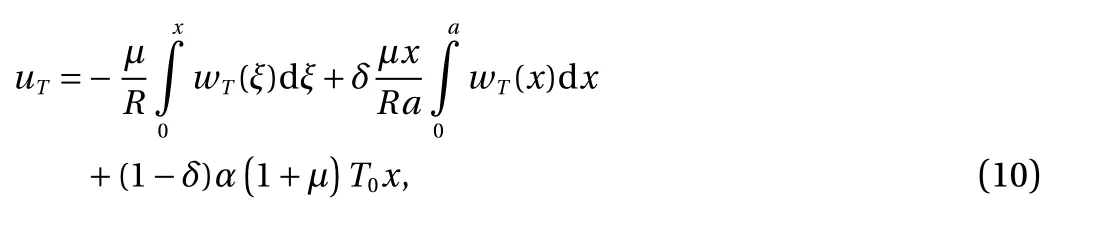
where

By virtue of Eq. (10) from Eq. (5) one can have:
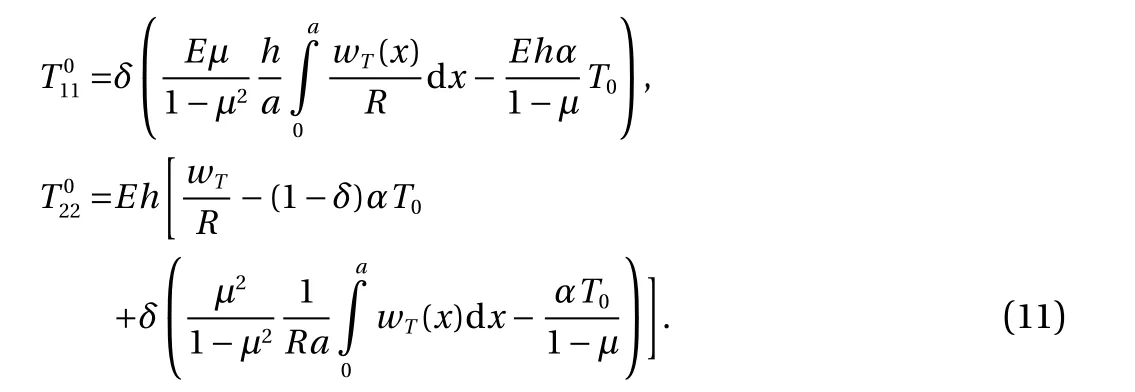
The problem of determining wTby virtue of Eqs. (5) and (9)reduces to solving the equation
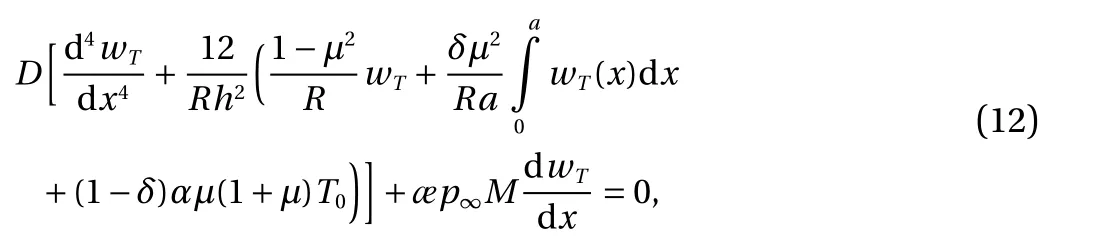
under the boundary conditions either Eq. (6) or (8). The solution of equation (12) that satisfies the specified conditions is obtained. It is not given here due to its bulkiness.
On the basis of assumptions (a)-(d) for the undisturbed state, similarly to Ref. [7], the following linear differential system of aerothermoelastic stability equations is obtained:
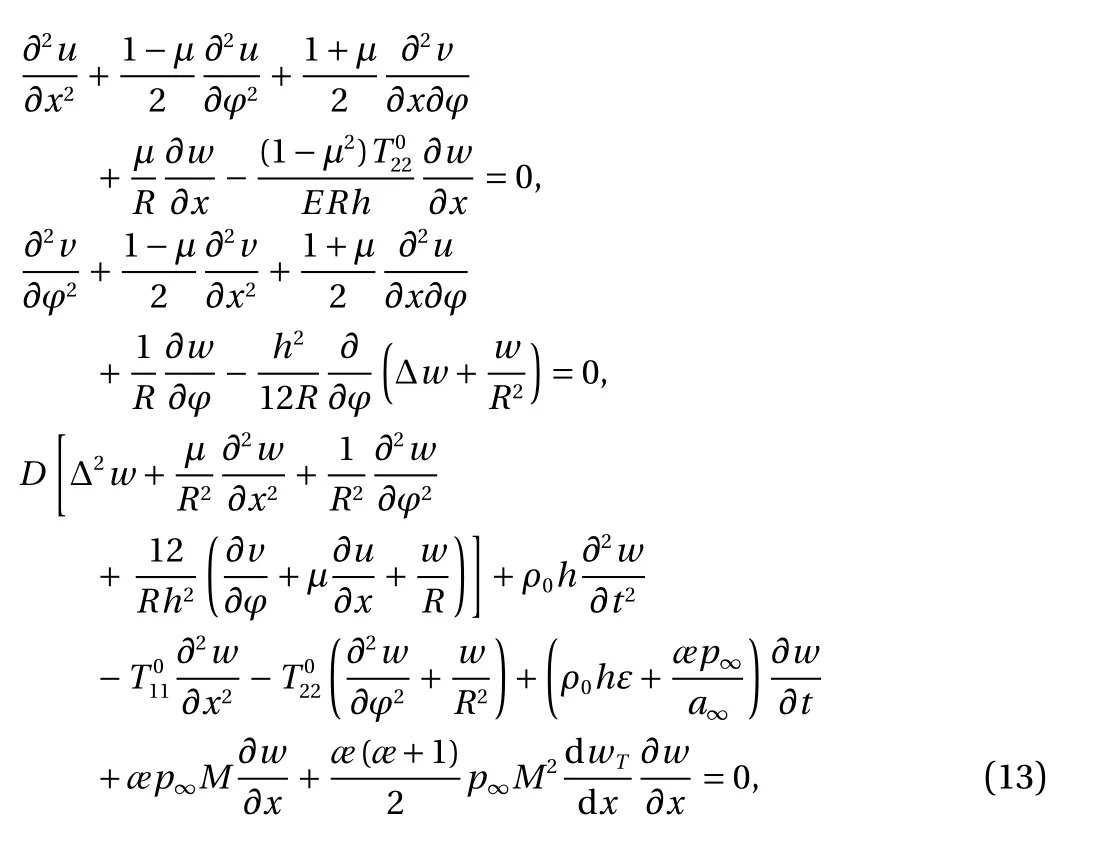
When solving specific problems of stability, the boundary conditions for disturbances coming from the edges fixing conditions are added to system Eq. (13). For example, if the edges of the shell are hinged and fixed, then the boundary conditions are represented as:

The solution of system Eq. (13), satisfying conditions Eq. (14)is presented in the form
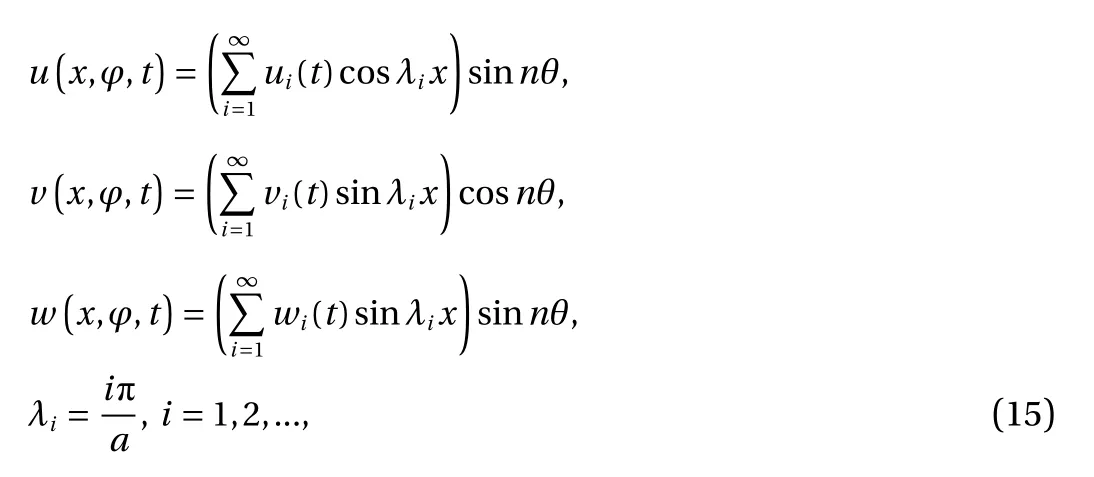
where ui(t),vi(t),and wi(t) are the functions of time t to be determined.
Substituting Eq. (15) into the system Eq. (13), applying the orthogonalization process and having restricted us with twoterm approximation, the unknowns ui(t),vi(t) are presented using wi(t). Substituting the obtained expressions into the third equation of the system (13), the system of ordinary differential equations is received with respect to unknown functions wi(t).Let us present the solutions of this system in the form wi=yieλt,from the condition of existence of nontrivial solution the characteristic equation is obtained with respect to λ. Using the Hurwitz theorem, in the case of two-term approximation, the instability regions and critical velocity values are obtained. Numerical analysis is performed and results are depicted in Figs. 1 and 2. These figures show the dependence of νcron the wave number n in a circumferential direction for several values of components of temperature field. Figure 1 shows that a) when the edges are free, a constant thermal field does not affect the value of νcrand b) depending on the wave number, νcrhas a minimum point.
Figure 2 shows that (a) variability of temperature field has a significant effect on the value of the critical speed ( νcrincreases)and this effect increases with the increasing n, and (b) the function νcr(n) has a minimum point, which depends on Θ.
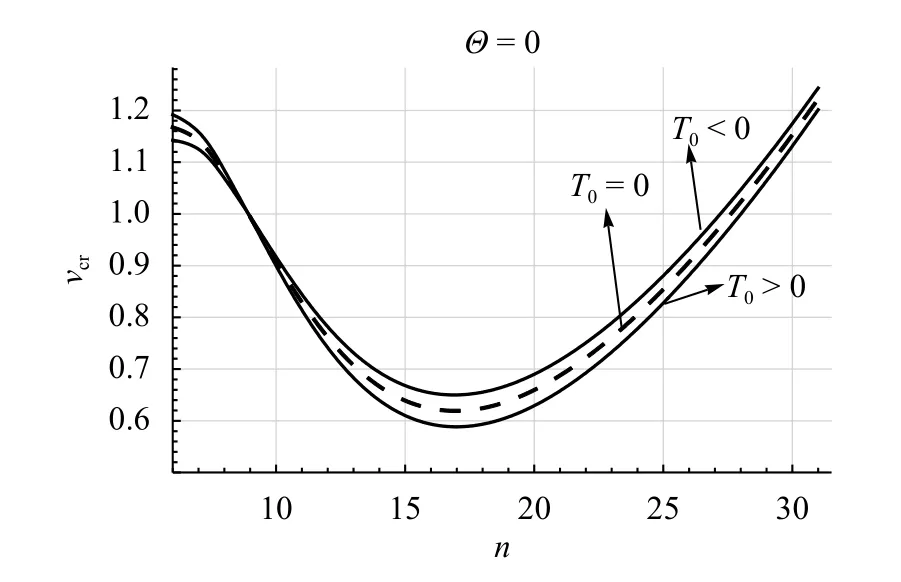
Fig. 1. Dependence of the critical speed on the wave number in the case of constant thermal field
Calculation are performed using α=2.38×10-5°C-1, k=1200 W/(m2·°C), λ=210 W/(m·°C), μ=0.34, a=1 m, h/a=1/100, and R/a=2.
Let us consider the case of axisymmetric problem, when the edges are fixed in the axial direction. In this case, having excluded the function u, the following linear differential equation is obtained from Eq. (13):
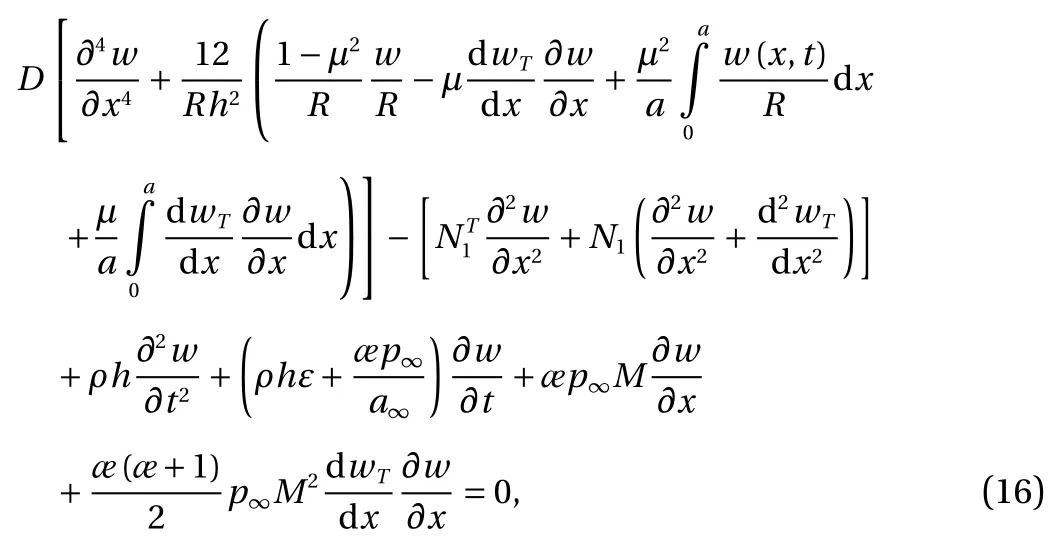
which solution should satisfy the simply supporting conditions
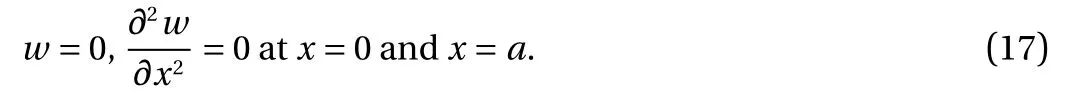
Let us note that in the examined case, wTis the solution of the problem Eqs. (16) and (17). The following notations are from Eq. (16) are used:

The formulated boundary value problem Eqs. (16) and (17) is solved by the Fourier method and the stability problem of the considered aerothermoelastic system is reduced to the investigation of the sign of real parts of the roots of characteristic equation, depending on the ambient speed and on the characteristics of the temperature field. As a result, the stability conditions are obtained and investigated numerically.
On this basis, in Fig. 3, a stability region is constructed on the plane ( ν,T0) - the case of a uniform temperature field ( Θ=0).
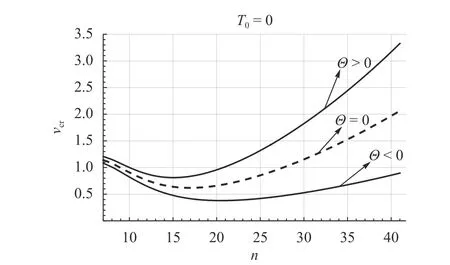
Fig. 2. Dependence of the critical speed on the wave number in the case of variable along the thickness thermal field
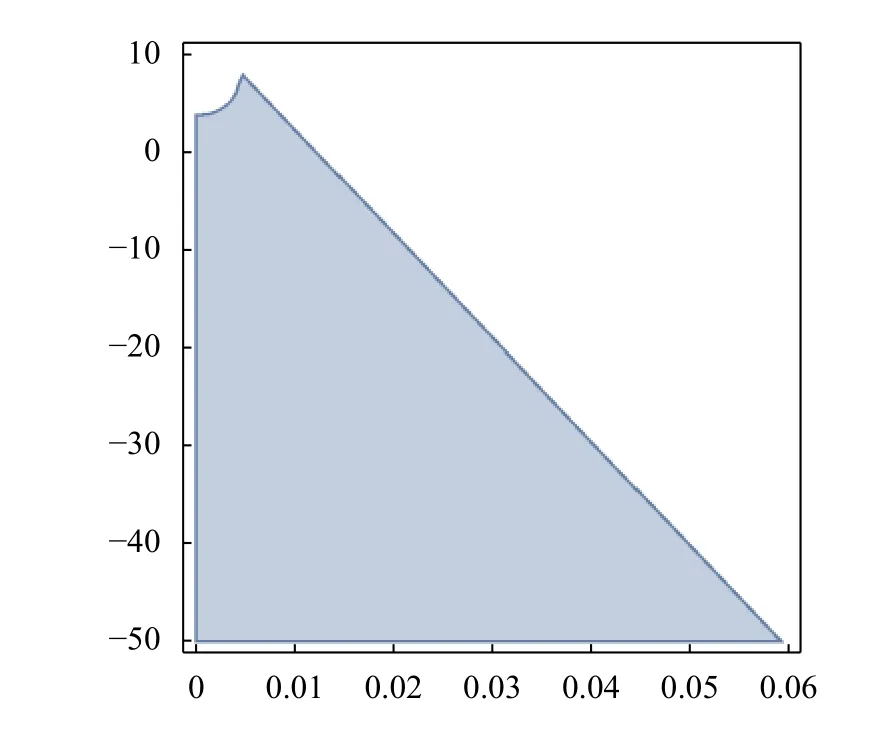
Fig. 3. Stability region on the plane
Figure 3 shows, that constant component T0of temperature field has a significant effect the stability of examined system.Namely, (a) if T0>0 then the temperature narrows the area of stability and reduces the value of the critical speed. Moreover,there is a positive value of a constant temperature field above which the cylindrical shell becomes unstable, (b) negative constant temperature leads to the expansion of stability region and to an increase of the value of critical speed.
The values of the critical speed of ambient supersonic gas are calculated for both homogeneous and variable temperature fields and are listed in Table 1.
The influence of a variable temperature field on the stability regions of cylindrical shell is also investigated. The numerical simulation shows that variable temperature field expands the region of instability for positive values and narrows it with negative values of the parameter Θ.
Table 1 The value of the critical velocity at different values of temperature (in °C)
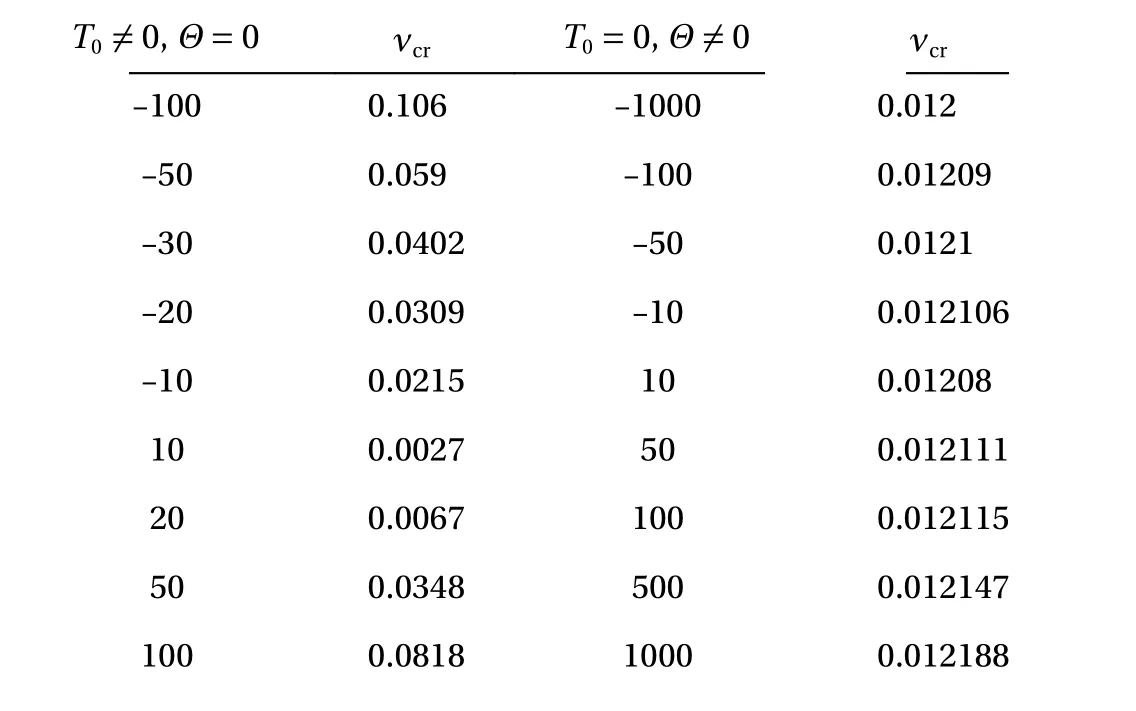
Table 1 The value of the critical velocity at different values of temperature (in °C)
T0/=0,Θ=0 νcr T0=0,Θ/=0 νcr-100 0.106 -1000 0.012-50 0.059 -100 0.01209-30 0.0402 -50 0.0121-20 0.0309 -10 0.012106-10 0.0215 10 0.01208 10 0.0027 50 0.012111 20 0.0067 100 0.012115 50 0.0348 500 0.012147 100 0.0818 1000 0.012188
Acknowledgements
The work was supported by the State Committee on Science and Education of the Ministry of Education and Science of the Republic of Armenia within the framework of the research project (No. SCS 18T-2C149).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Thermal Stresses
- Stresses of orthotropic laminated beams subjected to high temperature and mechanical load
- Transient thermal response of functionally graded piezoelectric laminates with an infinite row of parallel cracks normal to the bimaterial interface
- Stochastic transient analysis of thermal stresses in solids by explicit timedomain method
- 3D thermally induced analysis of annular plates of functionally graded materials
- Thermoelastic waves in helical strands with Maxwell-Cattaneo heat conduction
