Crashworthiness assessment of thin-walled double bottom tanker: A variety of ship grounding incidents

Adity Rio Prowo, Sukmji Indro Chyono, Jung Min Sohn

a Department of Mechanical Engineering, Sebelas Maret University, Surakarta, Indonesia

b Department of Naval Architecture and Marine Systems Engineering, Pukyong National University, Busan, South Korea

Keywords:Bottom raking Ship stranding Finite element analysis Crashworthiness criteria Progressive structural failure

A B S T R A C T This study addresses the issue of ship accidental grounding as an impact phenomenon, with the assumption that an interaction of its structure with the oceanic seabed (obstruction), idealized as rock topology, is capable of initiating a so-called hard ground scenario. This occurrence variation was considered by performing two main instances, encompassing raking and stranding, often experienced by oil/chemical tankers as thin-walled structures. In addition, a failure criterion was implemented on the structural geometry, in order to define its ultimate limit and possible damage,during interaction with the obstructions. Subsequently, the analysis results were compiled to assess structural crashworthiness as well as progressive failure of the double bottom part of the tanker, where energy criterion indicated the raking to be more destructive. Meanwhile, detailed observation of the failure sequence indicated the stranding to have successfully breached the inner bottom shell.

Inspired by developmental advances in engineering and technology, international maritime societies make fashion shifting attempts from general rules to specific regulation per individual ship. Meanwhile, factors related to these changes are also affected by the rising demand for safety prediction, and the wide range of crashworthiness assessment for marine and offshore structures, especially against various accidental loads. Recently,Lloyd's register report placed collision and grounding as highest,in terms of the causative elements of maritime pollution from early 1900s [1, 2]. Initially, a concern of ship structure against these accidental loads were addressed on a nuclear powered ship by Minorsky [3], whose proposal in empirical formula was subsequently developed by several scholars [4-6]. In addition,grounding is also deliberated to be as dangerous as collision,based on a series of related theories described by Simonsen [7].Furthermore, the collaboration of analytical approach [8], actual experiment [9], and numerical analysis in solving thin-walled structural problem, were also considered in evaluating the validity of each calculation method, e.g. by Muttaqie et al. [10].

Advancements in the development of computational instruments in recent decades have presented more acceptable methods to conduct structural assessment. Meanwhile, in the fields of impact engineering and marine structures, ship grounding was analysed using a collaborative strategy of the mentioned approaches, where the computational technique of finite element(FE) was selected as the main methodology. This phenomenon,in line with other events, e.g. collision and explosion, were continuously observed collectively with other forms of marine-steel impacts, encompassing accidents by various parties within last five years, where the results of FE were judged to reach satisfaction [11-23]. In addition, a number of these works show a trend line, which indicates that impact phenomena comprises numerous problems that have not been solved. Furthermore, Alsos and Amdahl [24] stated “Ship grounding is a very complex significantly nonlinear process, with the possibility of severe consequences”, and comparative studies to assess crashworthiness of marine structures against various impact scenarios were continuously required for safety development. Therefore, there is need for further research to evaluate this parameter for existing structural design.

This research is, therefore, aimed at calculating the structural responses and crashworthiness criteria of a double hull tanker under ship grounding, using a verified FE methodology. Furthermore, a comparative study accounting for a variety of penetration types and selected impact parameters was also conducted as the main discussion. In addition, bottom raking and ship stranding were assumed as impact scenarios to be encountered by the tanker, and effects of the external parameters, including impact location and obstruction topology were also considered in the detailed observation of structural responses for each case study. Meanwhile, progressive failures were presented with the extent of bottom damage, in order to provide complete response estimations.

A set of terminologies was set to identify the entities involved in the present study, where the bottom structure was modelled as a 17000 dead weight tonnage (DWT) chemical tanker with the following principal dimensions provided: overall length (Loa=144 m), breadth (B = 22.6 m), depth (H = 12.5 m), and draft (T =9.1 m). Furthermore, the geometry model (Table 1) was built in the form of two tank length, in order to reduce the interference of boundary conditions, and the following description shows the entity to be denoted as structure, and Table 1 demonstrates scantling data and plate thickness for the bottom. Moreover, the 4-node shell element was selected to further arrange the structure in FE analysis through the use of explicit codes ANSYS-LS DYNA [25], due to its suitability in nonlinear problems, included in the characteristics of grounding (impact). Furthermore a lumped mass matrix was required during the simple inversion stage, which was not necessary in the stiffness matrix because all nonlinearities (including contact) were contained in the internal force vector (see Eqs. (1) and (2)), towards which, major computational efforts were directed and no convergence checks were needed, as the equations applied are uncoupled. However,it is important to maintain stability limit (Eqs. (3)-(6)), set as very small time steps, and the subsequent finite element assessment was obtained as a calculation instrument. Therefore, it is important to understand the initial conditions as well as the constitutive relation of the fundamental algorithm described in (Eqs.(7)-(11)). In addition, for the explicit method, a central time difference integration method was used, and the physical components were evaluated in the order of acceleration, velocity and displacement, in order for the initial condition to be updated,based on a set of assumptions and boundary condition

where M is the mass matrix of the model,is the applied external and body force vector,is the internal force vector, atis the acceleration of the system at t, BTis the strain, σnis the internal stress, Ω is the solid volume, Fhis the hourglass force,Fcis the contact force, t is the observed time, Δ t is the time step size, Δ tcritis the critical time step size, ωmaxis the largest natural circular frequency, c is the wave propagation velocity, l is the rod length considered in the algorithm assumption, E is the Young's modulus, and ρ is the specific mass density (note: the critical time step size for explicit's time integration depends on element length and material properties (sonic speed)).

Table 1 Scantling data of the tanker's double bottom structures.

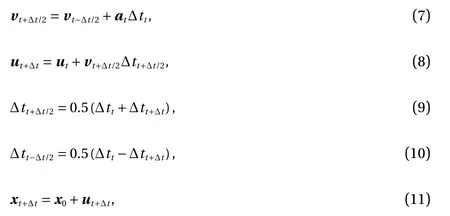
where vtis the velocity of the system at t, utis the displacement as result of the velocity of the system at t, x0is the initial condition of the modelled system or geometry, xtis the updated displacement/conditio of the modelled system in numerical analysis, and Δ t is the time step size.

The fully integrated shell formulation of Belytschko-Tsay was applied to the geometry, in order to avoid inaccuracy in deformation, due to the hourglass mode, and the structure was implemented by a deformable characteristic, in an attempt to assess the structural damage under several grounding situations. This was further defined through the nonlinear inelastic model considered using the plastic-kinematic material model, applying the mathematical formula shown in Eq. (12), as well as the properties in Table 2. Furthermore, hardening number for the steel AH36 was assumed to possess only kinematic hardening, leading to 0 numbers in its exponent

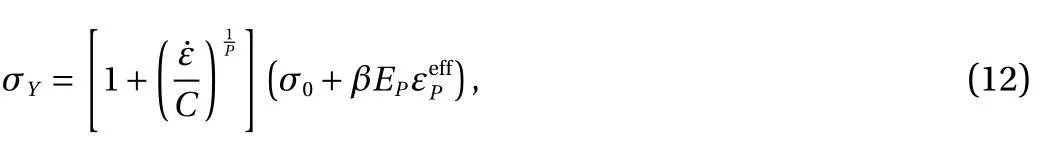
where σYis the yield stress,is the strain rate, C and P are the Cowper-Symonds strain rate parameters, σ0is the initial yield stress, β is the hardening parameter, EPis the plastic hardening modulus, E is the elastic modulus, andis the effective plastic strain.

During the interaction with oceanic obstructions, heavy damage is often expected on structures, including the rupture of shell, girder crushing etc. The definition of failure criterion in the acquisition of precise damage extent estimation was considered to be a necessity. Therefore, failure in this study was described as a condition of any structural component (plate, stiffener, girder or frame), which surpassed its strain limit, after experiencing excessive plastic deformation, due to contact with an oceanic obstruction. In addition, mesh size was also considered an important aspect in impact analysis as it affects deformation, therefore,the recommended criterion of Det Norske Veritas-Germanischer Lloyd [26], as shown in Table 3 and Eq. (13), was used to calculate mesh size for the ship model

where εfis the failure strain, εgis the uniform strain, εeis the necking strain, t is the plate thickness and leis an individual element length.

Based on grounding analysis, as interaction between the structure and obstruction was expected, it was necessary to consider friction value as part of contact properties. This was generally taken according to Coulomb friction coefficient, within the ranges of 0.2-0.4, as previously adopted by Simonsen and Wierzbicki [27]. Furthermore, variation in its implementation may occur, taking cognizance of the conditions of underwater hull surfaces, especially bottom and bilge plates, which in many cases become slippery, due spilled oil and marine plants.However, the assumption of roughness, as influenced in the manufacturing process is also capable of affecting other factors,and this study adopted the standard value for steel-rock interaction (0.3) in the assessment.

Besides the description of structure, the seabed detail were also presented and modelled as the solid-rigid material, in order to idealise hard-grounding situation, hence, designed to absorb all impact energy and deformation processes. Furthermore, the summary of the obstruction material models are presented in Table 4, where the seabed was determined to consist of two topologies. In addition, the conical form was assumed as rock(shown in Fig. 1), and applied by the Plagioclase f. This was subsequently used in the comparison of structural crashworthiness,under raking and stranding.

The initial grounding analysis was addressed to detect the structural behavior of double bottom under:

(1) raking, which was designed to be experienced by three targets, including center, and side girder, as well as the spaces between, as illustrated in Fig. 2. Meanwhile, these scenarios placed the conical obstruction in-line to the ship model, applying a uniform velocity of 10 m/s. Furthermore, the marine steel AH 36 was embedded on its structural geometry, while the FE simulation time was terminated in tsim= 0.4 s;

(2) using this same setting, the next analysis was organized to observe structural nonlinearities under ship stranding, where the obstruction obtained the velocity to move in the vertical direction (z-axis), while other translations were restrained. Conversely, the bottom structure was set to be fixed in the initial position, with constraint applied at the edge of the inner bottom and bilge plates, while rotational and translational displacement of the structure were fully restrained.

Different targets were selected as a result of varying locations of the conical obstruction, as this scenario required it to be placed below the double bottom, with the structure penetrated in lateral direction. Moreover, the target for this accidental case was determined to be three locations, i.e. x-intersections, and spaces between girders and floors (see Fig. 3), with the assumption that stranding took place during rough sea and the ship experiences slamming and contact with seabed, therefore, applied velocity is lower than the raking scenario, where 5 m/s was considered. This theory is believed to be reasonable as the phenomenon occurs during heavy storm or violent waves, which enables ship slamming and pitching, during vertical collision, andcontacts with seabed. Conversely, raking mostly happens during a forward sail in powered-condition [28], making the applied velocity to be generally greater than observed in stranding. This allows the obstruction to move in the vertical direction, with the bottom structure located above it, whose rotational displacement was set as 0, while the ship is fixed on a position.

Table 2 Properties of the material models in FE simulation: double bottom structures.

Table 3 Proposed constant value to estimate failure strain accounting for mesh size [26].

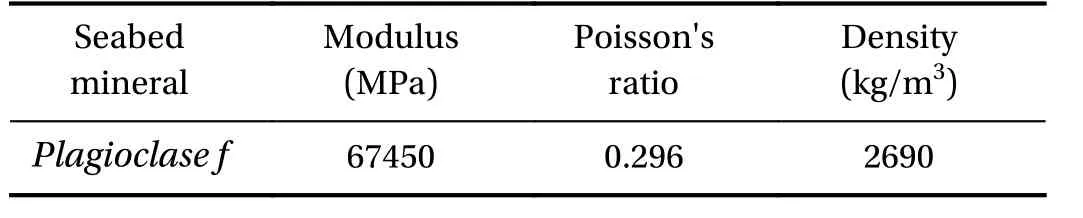
Table 4 Properties of the material models in FE simulation: oceanic obstructions.

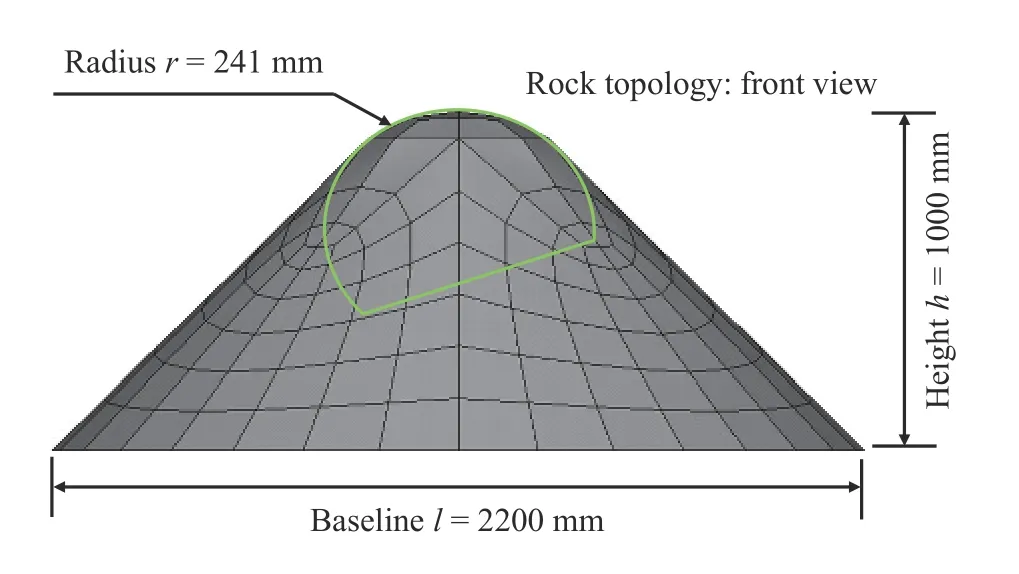
Fig. 1. Geometry and configuration of the selected oceanic obstructions: conical geometry to compare raking and stranding scenarios.

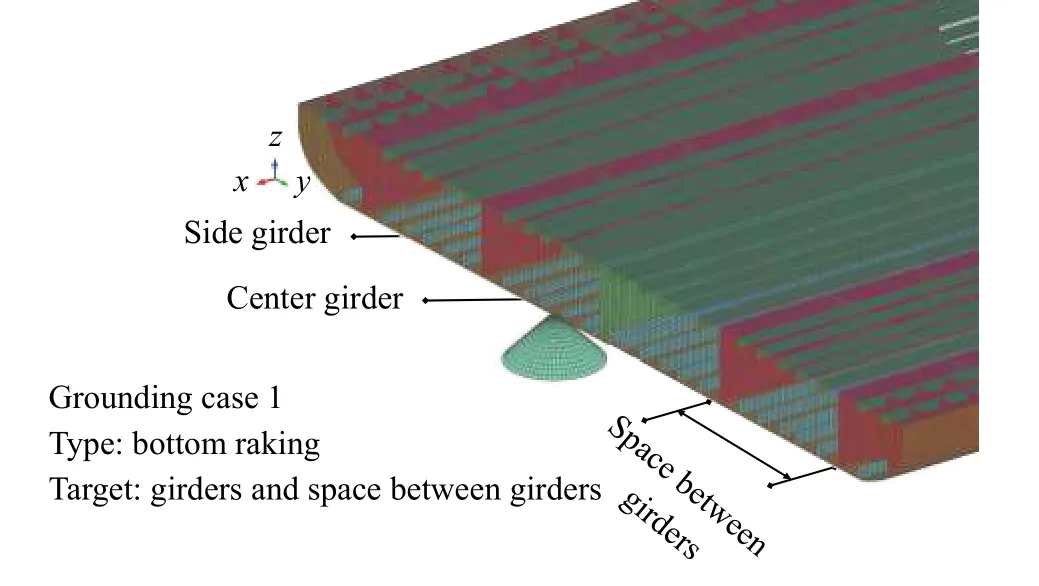
Fig. 2. Grounding scenario for the first case, bottom raking.

Observation of the structural response was conducted by assessing structural crashworthiness during the interaction of the ship against grounding actions. Firstly, this discussion was addressed through absorbed energy, using the calculation by FE approach, acquired in forms of the internal energy. This was further defined as the amount of energy necessary to plastically deform the involved colliding entities, computed based on the six components of stress and strain (tensorial values). Furthermore,Eq. (14) presents the value of all elements (of the discrete model structure), which were summed to attain the total internal/absorbed energy

where Ea-newis the updated absorbed energy, Ea-oldis the initial absorbed energy, σ is the acting stress, Δε is the incremental strain, and Ω is the solid volume.

In the grounding scenario, deformation was fully experienced by the double bottom structure, where the obstruction was defined as rigid. Meanwhile, after three targets collision occurred in the raking case (Fig. 4), it was observed that the center girder absorbed the highest energy level, followed by the side girder, and subsequently the spaces between girders. This phenomenon took place because less structural components were located in the space between girders, therefore, the girders on the double bottom have been reported to play a significant role in the energy absorption process.

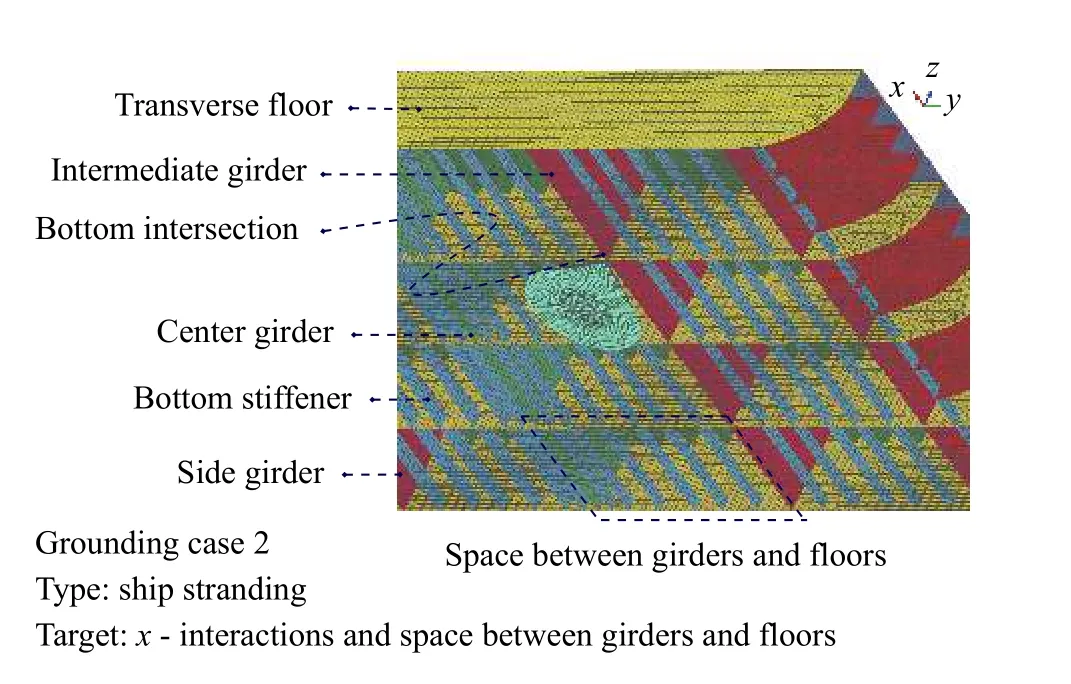
Fig. 3. Assumed scenario of the second case, ship stranding.

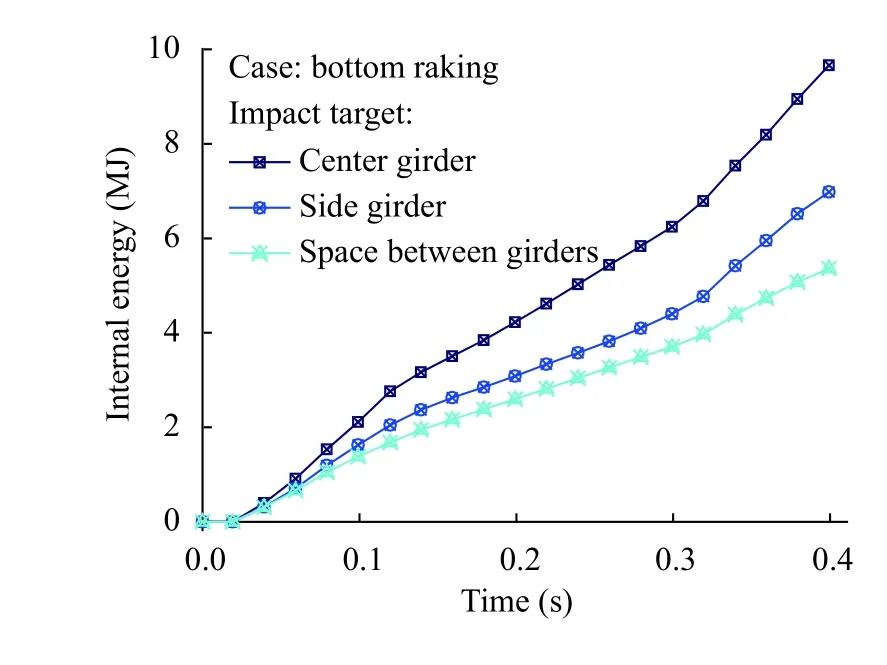
Fig. 4. Absorbed energy for three targets in the raking case.

Fig. 5. Tendency of the crushing force in ship grounding.

In the raking instances, force behavior for the three targets(Fig. 5) concluded that the highest magnitude was achieved by the center girder, confirming the behavior of absorbed energy during structure-rock interaction. This result also showed high fluctuation during early contact, because it occurred as a deformation due to interaction with the obstructions' steep angular distance, which happened on several structural components at the same time, including the lower parts of the bottom shell,and the transverse floor. Furthermore, a clearer presentation of this phenomenon is discussed in a comparative investigation between two obstructions possessing different geometric angular distance in the subsequent paragraph. Meanwhile, following the transition of the high fluctuation period (with range tsim=0-0.15 s), the fluctuation forces were reduced to certain points at the same time of damage expansion on the girders. Conversely,through stranding, the fluctuation style of the crushing force was expected to possess a significant pattern with the current raking case. In addition, the phenomenon in this initial statement is highly possible to take place as it is possible for the obstruction to interact with different components on the bottom structure,and subsequently penetrate the determined targets in different directions.

Ship grounding involves high absorbed energy and crushing force while deformation occurs on the bottom structure, and the subsequent assessment of structural crushing and progressive failure (Fig. 6) are also required, according to penetration sequence. Meanwhile, the initial condition as shown in Fig. 6 indicates the structure to be in good condition, where the obstruction had not moved to the designated target, and the lower part of the transverse floor began to fail in the time range simulation tsim= 0.05-0.10 s. In addition, damage expanded to the bottom shell, stiffener and center girder in tsim= 0.15 s, and it was noted that during tsim= 0.20 s, the obstruction reached approximately half the distance between two girders. Furthermore, the destruction continued to expand on the lower part of the double bottom structure, where the second transverse floor was penetrated at tsim= 0.35 s, and this was finally breached at the end of ship grounding (tsim= 0.40 s). Based on the behavior, the bottom plate was concluded to be the most deformed component, as it absorbed the strain energy under raking scenario at approximately more than 1.5 and 2.5 MJ, during collision with side (left side of Fig. 6) and center girders (right side of Fig. 6), consecutively. However, the latter seemed to exhibit a more significant impact at the bottom stiffener than the girder itself, possibly due to the narrow arrangement. Moreover, components on the lower part of the double bottom, including shell, stiffener and center girder collapsed during interaction with the obstruction.

It was also observed that the damage width was similar with the maximum diameter of the rock obstruction at the interaction point (see illustration in Fig. 7), confirmed by the raking scenario on the side girder, which surpassed the stiffener, in terms of absorbed energy. This situation took place and was influenced by the space in the impacted location, which was wider than the position near the center girder. Therefore, the top-three contributions of the structural resistance were presented by bottom plate, side girder, and bottom stiffener, while for the transverse floors, after the first was breached approximately after tsim= 0.10 s, a constant state was experienced as no energy fluctuations were observed. This was predicted from the result because after a breach, failure was observed on the bottom plate,stiffener, and girder, while no influence was indicated on the floor. Furthermore, fluctuations began to occur again as the second floor experienced the deformation process, due to an advance penetration by the obstruction, hence, it was also noted that, in case studies of center girder raking, failure of the side was not spotted, and vice versa.

Other cases of typical grounding occurred in form of stranding, where structural deformation were expected in instances where the seabed is formed, either by sandbank [29] or hardrock geometry, as analysed in this research. Moreover, absorbed energy showed a difference in tendency and extent, when compared with the raking case (see Fig. 8). The tendency of the intermediate girder, and space between girders-floors produced increment in range tsim= 0.20-0.30 s, which was earlier than the raking case. In addition, the energy magnitude was also lower,where the center girder in raking produced almost 10 MJ (Fig. 4),while the girder-floor intersection demonstrated approximately 8.6 MJ (Fig. 9), which took place as the impact velocity was reduced as assumed in previous sections. Conversely, a similar trend was achieved in both cases, although the part of the double bottom, strengthened by girder under raking was more significant, while that of the girder and floor in stranding, produced a higher absorbed energy in comparison with other targets. This criterion also confirmed the significant role played by the longitudinal girder in providing resistance for both longitudinal impact to t-intersection (consisting of transverse floor, bottom plate, and girder) during bottom raking, and x-intersection(same components as the t-intersection) in ship stranding.

Crushing force was verified by fluctuation, as seen in Fig. 8.In the stranding analysis, peak magnitude occurred approximately within the time span of tsim= 0.10-0.20 s, where the obstruction approached and surpassed half the height of the bottom structure. Furthermore, the force reduced as the maximum diameter of the obstruction initiated similar extent of damage on the bottom plate, hence, the crushing force increased again, as the deformation process of the inner bottom shell was commenced. In summary, the tendency of crushing produced was satisfactory in terms of absorbed energy for the different targets,and a higher fluctuation of girder-floor intersection indicated better capability of resisting penetration, when compared with other targets.

In terms of the bottom structure, the initial indentation on its plate was initiated at tsim= 0.05 s, followed by a deformation on the lower part of the girder-floor intersection. This component was penetrated continuously, in addition to the expanded damage at the bottom shell. Furthermore, after tsim= 0.35 s, the deformation stopped, due to it been completely breached, while the destruction of the inner shell began, concurrently. Subsequently, with the given setting, the tip of the rock seabed was observed to have successfully penetrated the inner bottom shell,and the descriptions of the progressive crush were confirmed by the damage sequence of the structural components shown in Fig. 10. This compared its behavior under stranding conditions on the intermediate girder (left side of Fig. 10) and girder-floor intersection (right side of Fig. 10), of which both produced similar tendency, where the bottom plate was entirely penetrated at about tsim= 0.3 s. Nevertheless, the absorbed energy during the interaction with the intermediate was lower than that of the girder-floor collision. This propensity was previously observed using the crushing force (Fig. 8) and the energy (Fig. 9), generally, although the specific reason is non-existent of the transverse floor on the intermediate girder, which significantly reduced structural resistance against stranding. Furthermore, assessing the terminal state of progressive failure in tsim= 0.35-0.4 s, the inner bottom shell was observed to be in a similar condition, i.e. successfully penetrated by the conical obstruction.

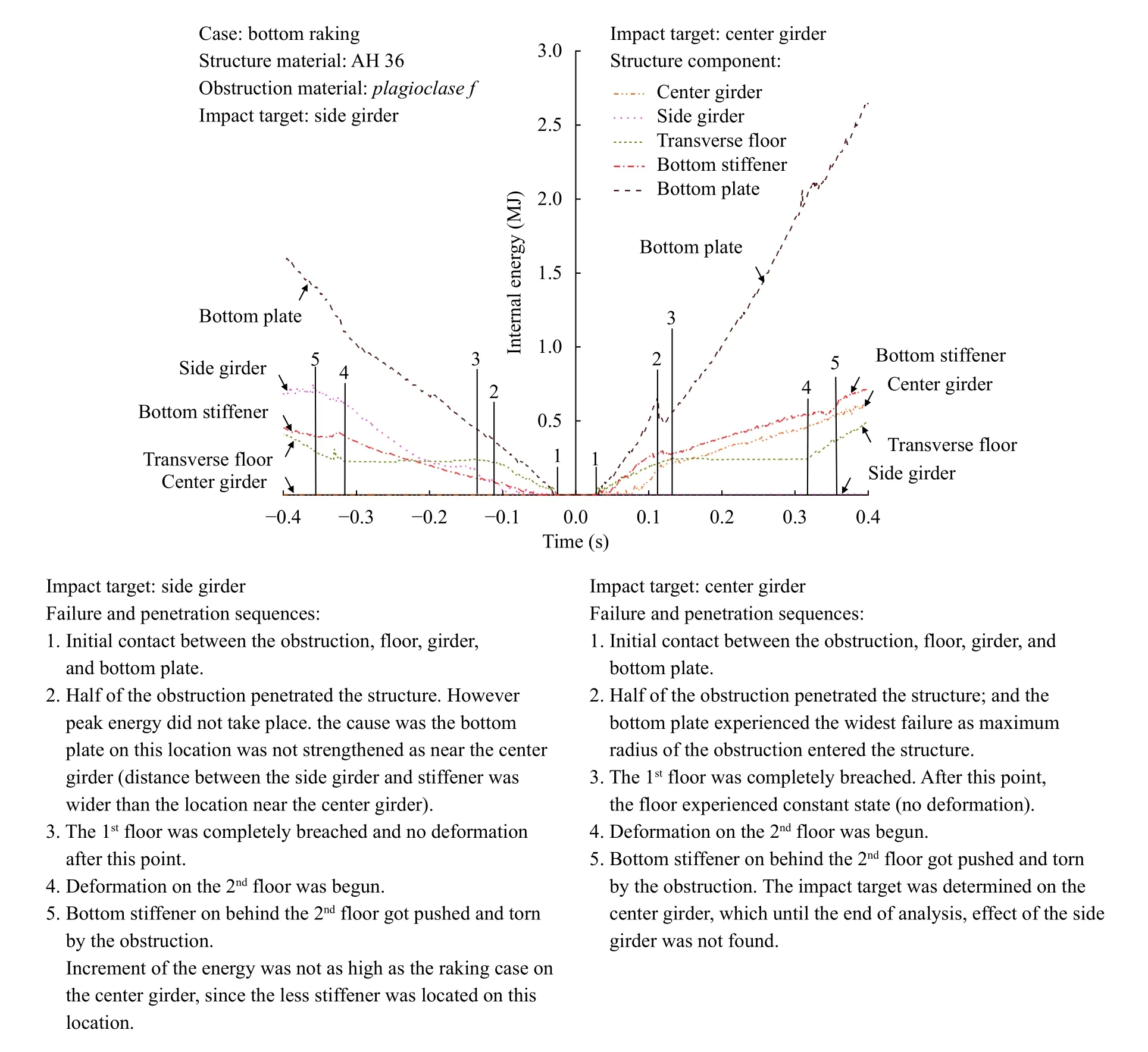
Fig. 6. Damage sequence of double bottom in the bottom raking case: main graph and description list of the graph.

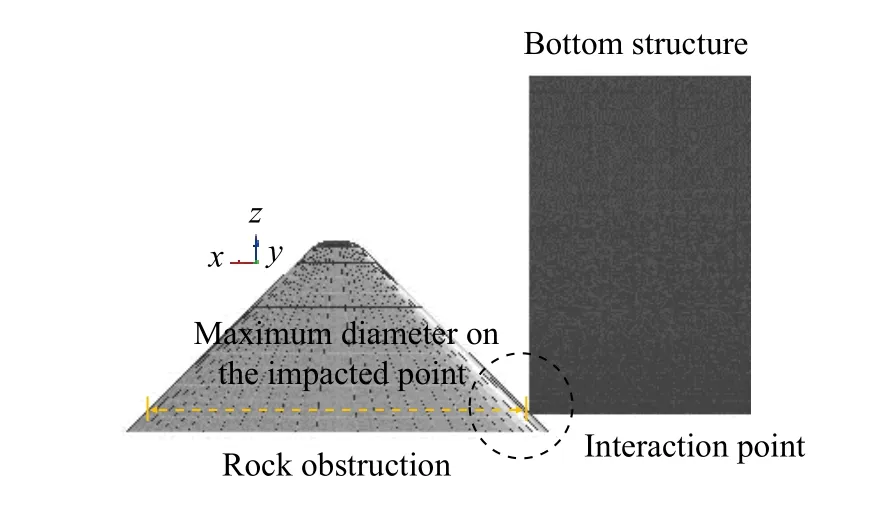
Fig. 7. Brief illustration of the maximum diameter of the obstruction on the interaction point. The point is highlighted by dark blue circle, and the diameter in this point is denoted by orange arrow.

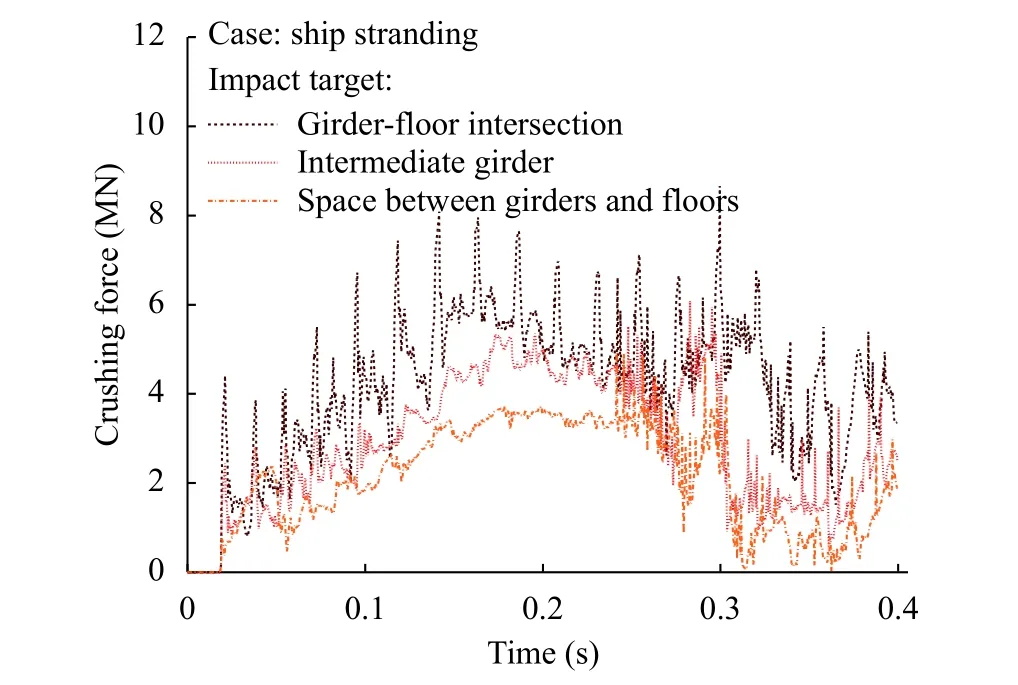
Fig. 8. Tendency of the crushing force for the ship stranding.

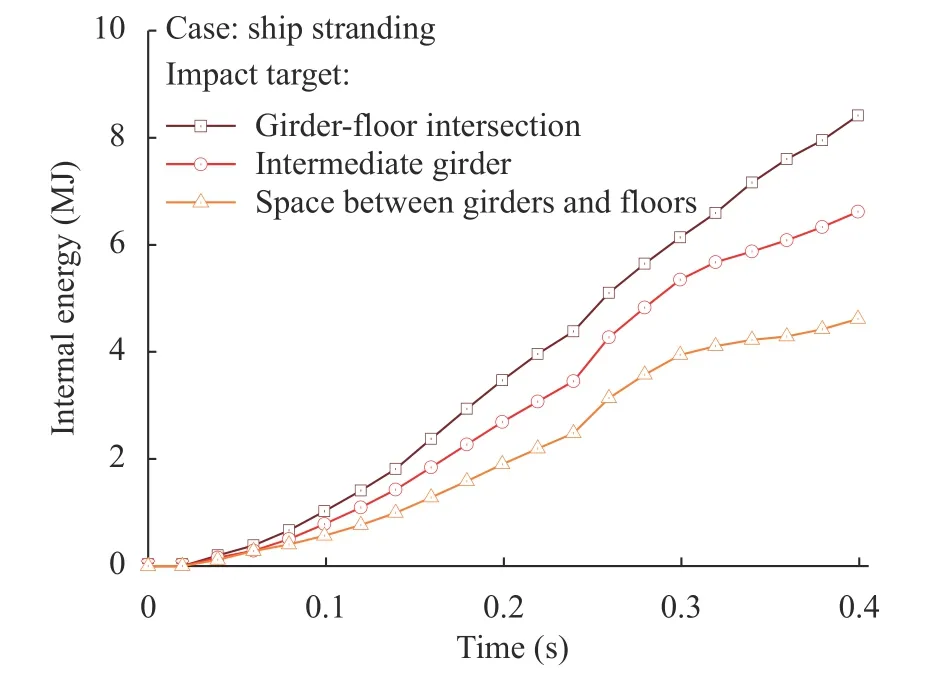
Fig. 9. Absorbed energy for three targets in ship stranding.

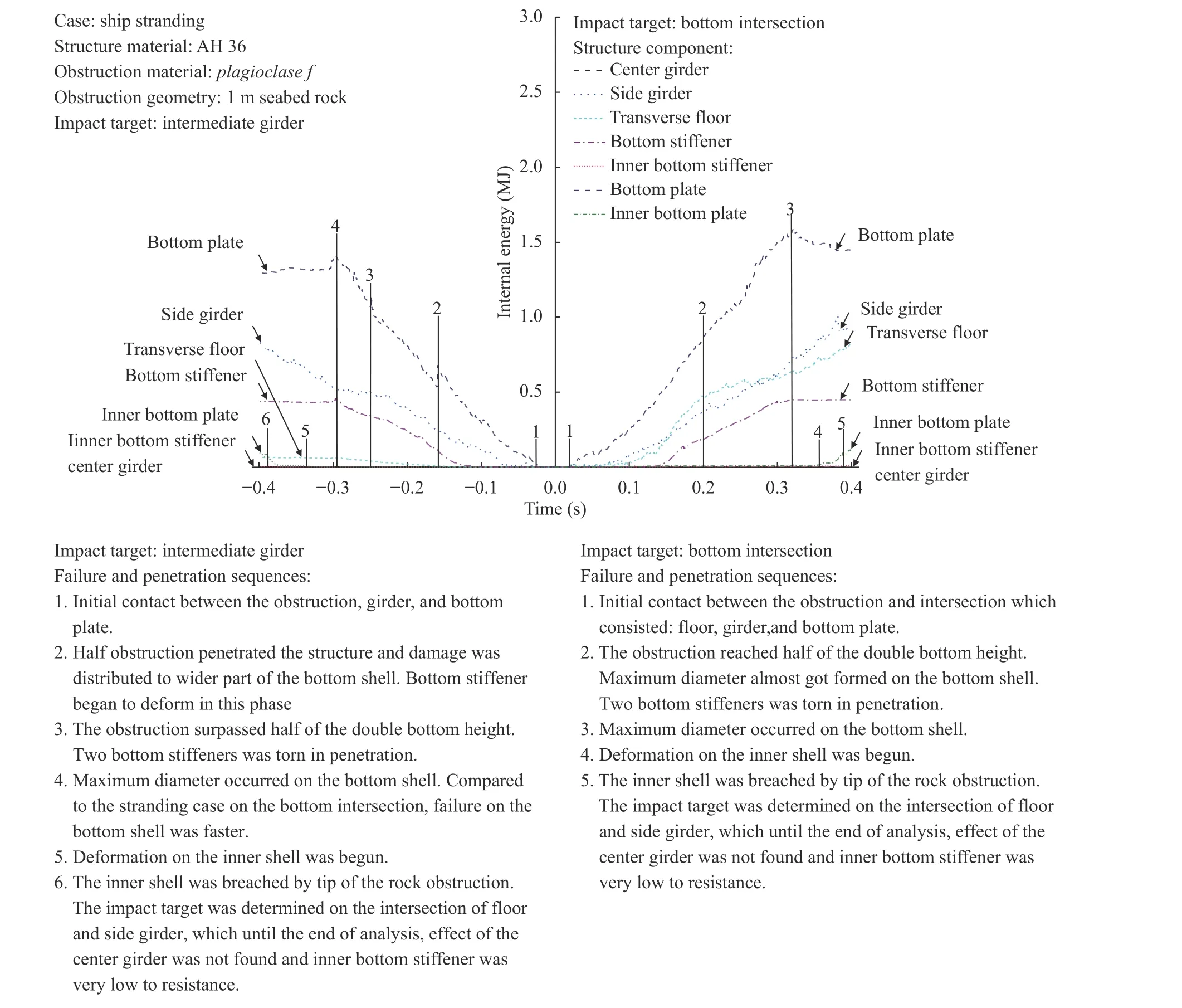
Fig. 10. Damage sequence of double bottom in the ship stranding: main graph and description list of the graph.

This research presented a series of crashworthiness assessment on several grounding cases, which were conducted to evaluate the behavior of a double bottom structure against a variety of impact load. These phenomena were considered, and the absorbed energy criterion indicated raking scenario to be more lethal to the ship structures compared to stranding cases, because it was capable of producing severe damage in the longitudinal direction. However, in view of cargo safety, the latter required serious attention, as it is observed at the end of simulation that the inner bottom shell was breached by the obstruction.Furthermore, during full-load condition, massive oil spillage is expected to occur in the chain reaction, specifically on the tank space between the girders and the floors, which were noted as critical. This was concluded after observing the summary of failure progression. Moreover, it was observed that the bottom shell and girder were vital in providing resistance in cases where grounding occurs on ship's double bottom, and its arrangement differs for raking and stranding cases, leading to a variety of crashworthiness tendency. In the global form, it is possible to observe this distinction in terms of the crushing force, which entails the initial contact, as raking produced significant increment due to frontal interaction with the surface on the transverse floor strengthened by the stiffener, girder and floor at the same time. However, the stranding scenario presented with a gradual increment, reaching the ultimate point, where the obstruction fully entered the structure.